2025年JCR一区新算法-回旋镖气动椭圆优化算法Boomerang Aerodynamic Ellipse(BAE)-附Matlab免费代码

介绍了一种受飞行中回旋镖气动行为启发的新型元启发式优化器，明确建模释放角度和发射力如何塑造其轨迹。为了克服现有算法有限的局部搜索能力，本文提出了一种基于气动椭圆效应的均匀局部挖掘策略，并将这种机制嵌入到回旋镖运动模型中，以创建回旋镖气动椭圆优化器。于2025年7月最新发表在JCR 1区，中科院2区 SCI 期刊 Mathematics and Computers in Simulation。

1.回旋镖气动椭圆优化器

在第3节中，提出了一种用于图像多阈值分割的元启发式算法。尽管已经提出了许多元启发式算法，但那些为多级阈值图像分割开发的算法在精度和适应性方面仍然存在局限性。针对这些问题，本文介绍了回旋镖气动椭圆优化器。首先，介绍了启发式机制，然后通过机制逻辑推导出公式。回旋镖是一种物理工具，被抛出并飞回其起点，在空中有一个弧形。
回旋镖算法主要受到回旋镖在空中的运动轨迹受投掷时角度和力的影响的启发，通过构建回旋镖投掷角度和力模型完成解的迭代更新。此外，从回旋镖投掷时的气动效应推导出一种基于气动椭圆效应的均匀局部挖掘策略。该策略可以使算法在优化过程中在小范围内进行密集搜索，不仅增加了算法的优化性能，而且更适合解决高维复杂图像的多阈值分割问题。

1.1灵感

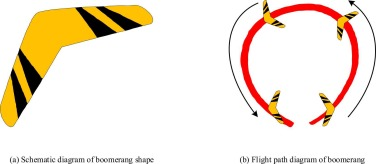
回旋镖，其形状在图2（a）中为“V”形，此外还有直翼、垂直翼和三叶形等其他形状。回旋镖是一种起源于澳大利亚土著文化的飞行装置。它与普通飞机不同，因为它有特殊的设计，可以让它在飞行过程中返回投掷者，如图2（b）所示。回旋镖也经常被演艺人员使用，他们通过使用不同的力量和不同的角度同时投掷多个回旋镖。在空中形成多个不同的动作并在观众的头部周围盘旋后，回旋镖在惊讶的咆哮和热烈的掌声中飞回表演者手中。

1.2 数学模型

由于回旋镖在空中轨迹受多重因素影响呈现不规则变化，本文将其运动轨迹建模为平滑弧线，并在此基础上建立回旋镖空中运动与旋转的数学模型。回旋镖气动椭圆优化器主要包括回旋镖空中运动规律和基于气动椭圆原理的均匀局部挖掘策略，先通过回旋镖运动模型完成解的全局搜索，再通过小邻域挖掘完成基于气动椭圆效应的均匀局部开采。

1.2.1 模型初始化

算法执行时首先生成满足边界约束的随机种群，第$i$个个体在第$j$维的组分表示为：
$$x_{i,j}=r_1\times (U{p}_j-Lo{w}_j)+Lo{w}_j\text{\hspace{1em}(11)}$$
其中：$x_{i,j}$：第$i$个解在第$j$维的值，$r_1$：[0,1]区间随机数；$U{p}_j$/$Lo{w}_j$：可行域上下界，所有维度组分构成合格解$X_i=[x_{i,1},x_{i,2},...,x_{i,n}]$，计算各解适应度后选取最优解$x_{Best}$作为精英解。初始化时记录每次投掷后解位置更新的最大变化量$max-dis$和最小变化量$min-dis$并置零。

1.2.2 回旋镖运动状态

情况1：基础运动状态
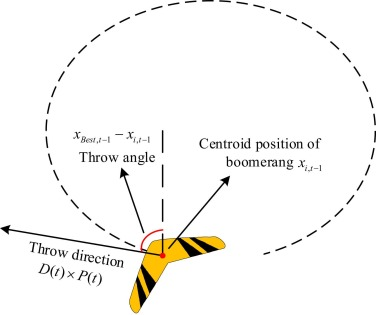
投掷时仅需考虑角度、力度和方向等因素，此时回旋镖未旋转可抽象为质点建模（如图5所示）。

1.3 回旋镖动力学模型

1.3.1 投掷力计算

每次投掷的回旋镖作用力$D(t)$为：
$$D(t)=maxdi{s}_{t-1}+mindi{s}_{t-1}\text{\hspace{1em}(12)}$$
其中$maxdi{s}_{t-1}$和$mindi{s}_{t-1}$分别表示种群个体投掷后的最大和最小步长：
$$\{\begin{array}{l}maxdi{s}_t=\max (x_{i,t}-x_{i,t-1})\\ mindi{s}_t=\min (x_{i,t}-x_{i,t-1})\end{array}\text{\hspace{1em}(13)}$$
式中：

• $x_{i,t}$和$x_{i,t-1}$：第$i$个个体在$t$和$t-1$迭代时的位置
• $i\in [1,N]$：个体编号，$N$为种群规模

1.3.2 投掷方向向量

投掷方向$S(t)$定义为：
$$S(t)=x_{Best,t-1}-x_{i,t-1}\text{\hspace{1em}(14)}$$
其中$x_{Best,t-1}$为第$t-1$代精英解。

1.3.3 投掷力衰减函数

随投掷次数增加的作用力衰减规律：
$$P(t)={\left(\frac{t-1}{T}-1\right)}^4\text{\hspace{1em}(15)}$$
$t$为当前迭代次数，$T$为最大迭代次数。

情况2：空中旋转运动
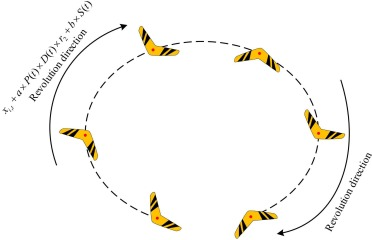
回旋镖被抛出后的运动轨迹呈从投掷点到回收点的弧线（如图6所示），此时旋转运动可视为对可行域空间的全局搜索。

回旋镖在空中旋转的数学表达式为：
$$x_{i,t+1}=x_{i,t}+a\times P(t)\times D(t)\times r_2+b\times S(t)\text{\hspace{1em}(16)}$$
式中参数；$a=0.3$：力度控制权重； $b=0.5$：方向控制权重 ；$r_2\in [-1,1]$：随机数；$D(t)$：投掷力度控制函数；$S(t)$：指向当前精英解的方向函数；$P(t)$：递减调节函数

该模型通过权重调节实现力度与方向的平衡，避免力度过大导致方向偏离或过度调节方向导致力度不足。
算法执行过程类比多次投掷回旋镖：

1. 随机生成初始投掷位置
2. 通过投掷运动搜索轨迹上的位置
3. 捕获每次投掷发现的最优解
4. 以群体最优解位置作为下次投掷方向

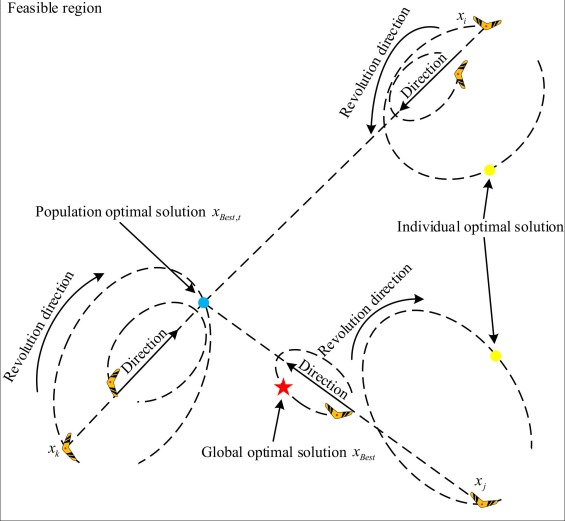
投掷力度由递减函数$P(t)$控制，既减少越界可能，又实现从全局搜索到局部开采的渐进过渡，最终通过迭代更新找到全局最优解。

1.3.4基于气动椭圆效应的均匀局部开采策略

通过对回旋镖在空中运动的分析，可以得出回旋镖的运动会在周围空气中产生空气动力学效应的结论。在本文提出的策略中，当可行域为二维空间时，将具有这种效应的区域近似视为椭球，将该区域视为解附近的局部搜索。因此，提出了一种新的策略，该策略对高维复杂目标函数具有可接受的时空复杂度和更好的搜索能力。
在策略中，每次迭代的部分解会在气动效应产生的局部区域中进一步搜索，相当于将局部区域表面的均匀随机抽样作为新生成的解集，该解集中的最优解成为迭代后的新解。根据启发式机制，该策略的目的相当于在三维空间中的椭球面上取离散且均匀的采样点。本文以三维为例，当问题维度为高维时，策略逻辑是三维的扩展形式。
当需要在椭球体上均匀取点时，我们可以先考虑在球体上均匀取点，因为在球体上得到的点可以通过线性变换一一映射到椭球体上，如图8所示。

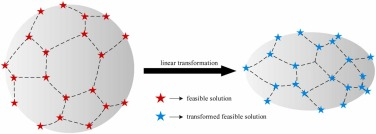
1.4 球面到椭球面的点映射

设球心为原点，$X$、$Y$、$Z$为相互独立且服从标准正态分布的随机变量，则点{X Y Z}T\{X\ Y\ Z\}^T{X Y Z}T在空间中的概率密度函数为：
$$f(x,y,z)={\left(\frac{1}{\sqrt{2\pi }}\right)}^3{e}^{-\frac{x^2+y^2+z^2}{2}}\text{\hspace{1em}(17)}$$

通过向量直径方向投影可在球面上生成均匀分布的随机点：
{x y z}T=rX2+Y2+Z2{X Y Z}T(18)\{x\ y\ z\}^T = \frac{r}{\sqrt{X^2+Y^2+Z^2}}\{X\ Y\ Z\}^T \tag{18}{x y z}T=X2+Y2+Z2​r​{X Y Z}T(18)
其中$r$为球半径，球面点分布概率密度（即球表面积的倒数）为：
$$u=\frac{1}{4\pi r^2}\text{\hspace{1em}(19)}$$

1.4.1 椭球面映射

设椭球三半轴长为$a\ge b\ge c>0$，通过线性变换将球面点映射至椭球面：
$$\left[\begin{array}{c}\xi \\ \eta \\ \zeta \end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& b/a& 0\\ 0& 0& c/a\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\end{array}\right]\text{\hspace{1em}(20)}$$
接受概率$p$的计算公式：
$$p=\sqrt{\frac{{\xi }^2{b}^2{c}^2+{\eta }^2{a}^2{c}^2+{\zeta }^2{a}^2{b}^2}{a^2{b}^2{c}^2}}\text{\hspace{1em}(21)}$$

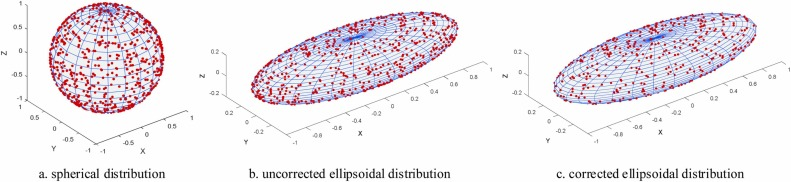
(a) 球面均匀分布 → (b) 线性变换后椭球面非均匀分布 → © 概率校正后的椭球面均匀分布
图9. 椭球体均匀随机取点。
回旋镖运动的气动效应可视为在以中心点生成的椭球体上进行随机均匀点搜索。首先，以当前解位置为中心生成一系列符合正态分布的点集，随后通过生成点集到原点的距离与半轴长度将其映射到高维椭球体上。同时，将公式(22)推广到更高维度，如下式所示：
$$p_{ij}=\sqrt{\frac{\min \left(h{r}_i^2\right)\times {\sum }_{k=1}^{\dim }\left(X{r}_{i,j,k}^2{\prod }_{l=1}^{k-1}h{r}_{i,l}^4{\prod }_{t=k+1}^{\dim }h{r}_{i,t}^4\right)}{{\prod }_{k=1}^{\dim }h{r}_{i,k}^4}}\text{\hspace{1em}(22)}$$

其中，$p_{ij}$表示以第$i$个回旋镖当前位置为中心生成的椭球体上若干回旋镖位置中第$j$个位置被接受的概率。本文中生成位置的数量设置为$10$，$h{r}_{i,k}$表示以第$i$个回旋镖当前位置为中心生成的椭球体第$k$维的半轴长度，其计算公式如公式(23)所示。$X{r}_{i,j,k}$表示以第$i$个回旋镖当前位置为中心生成其他卫星点时，第$j$个生成点的第$k$维坐标值。

$$h{r}_i=|x_i-x_{Best}|\times r_3\text{\hspace{1em}(23)}$$

其中，$h{r}_i$是以第$i$个回旋镖当前位置为中心生成的椭球体各维半轴长度组成的向量，$x_i$是第$i$个回旋镖的当前位置，$x_{Best}$是当前最优个体的位置，$r_3$是$[0,1]$内的随机数。

首先，可以随机选择部分个体进行气动搜索，本文中设置为种群规模的$\frac{1}{5}$。接着，需围绕选定的第$i$个回旋镖生成一组符合正态分布的点集位置，并将其映射到椭球空间，随后计算每个位置的接受概率，并通过接受概率判断是否选择当前点。最后，在所有被选点中找到最优解，与当前解比较并更新最优位置，如图10所示。

%  Boomerang aerodynamic ellipse optimizer: A human game-inspired optimization technique for 
%  numerical optimization and multilevel thresholding image segmentation.
function [Best_fitness,Best_position,Convergence_curve]=BAEO(Popsize,Maxiteration,LB,UB,Dim,Fobj)tic;Boomerang=initialization(Popsize,Dim,UB,LB);     BoomerangFitness = zeros(1,Popsize);             Convergence_curve=zeros(1,Maxiteration);    for i=1:PopsizeBoomerangFitness(1,i)=Fobj(Boomerang(i,:));end% Calculate the fitness values of initial boomerangs.[~,sorted_indexes]=sort(BoomerangFitness);Best_position=Boomerang(sorted_indexes(1),:);Best_fitness = BoomerangFitness(sorted_indexes(1));Convergence_curve(1)=Best_fitness;t=1;max_diff=zeros(Popsize,Dim);min_diff=max_diff;while t<Maxiteration+1Elite=repmat(Best_position,Popsize,1);alpha=((t-1)/Maxiteration-1)^4;beta=0.5;%% The stages of the boomerang movementBoomerang_1=Boomerang+0.3.*alpha.*(max_diff+min_diff).*(2.*rand(Popsize,Dim)-ones(Popsize,Dim))+0.5.*(Elite-Boomerang);max_diff=max(max_diff,(Boomerang_1-Boomerang));min_diff=min(min_diff,(Boomerang_1-Boomerang));Boomerang=Boomerang_1;% Out-of-bounds processingTp=Boomerang>UB;Tm=Boomerang<LB;Boomerang=(Boomerang.*(~(Tp+Tm)))+UB.*Tp+LB.*Tm;BoomerangFitness=Fobj(Boomerang);[~,sorted_indexes]=sort(BoomerangFitness);Boomerang=Boomerang(sorted_indexes(1:Popsize),:);%% Uniform local mining stage of boomerang% The number of generated positions can be adjusted according to different fitness value functionsn=10;                % Number of positionsfor i=1:round(Popsize/5)gv=abs(Boomerang(i,:)-Elite(i,:)).*rand(1,Dim);if sum(gv==0)>=1continue;end% Generation position and acceptance probabilityner_Boomerang=repmat(Boomerang(i,:),n,1);ads=random('Normal', ner_Boomerang, 1 ,n,Dim);round_point=ads;sum_point=0;qop=repmat(Boomerang(i,:),n,1);sum_point=sum(((round_point-qop).^2),2);sum_point=sqrt(sum_point);gv=abs(Boomerang(i,:)-Elite(i,:)).*rand(1,Dim);round_point=gv.*round_point./sum_point;p_point=0;sp=1;lv=cumprod(gv);sp=lv(Dim)^4;p_point=sum(round_point(:,:).^2*sp./gv.^4,2);lv=cumprod(gv);sp=lv(Dim)^4;if sp==0continue;endsp=sp/(min(gv)^2);p_point=p_point./sp;p_point=sqrt(p_point);% Select the generated location according to probabilityidx=(rand(n,1)<=p_point);rd_point=round_point(idx,:);point_num=size(rd_point);% Out-of-bounds processingTp=rd_point>UB;Tm=rd_point<LB;rd_point=(rd_point.*(~(Tp+Tm)))+UB.*Tp+LB.*Tm;if size(rd_point,1)==0continue;endnew_pointfit=Fobj(rd_point);[~,sorted_indexes1o]=sort(new_pointfit);new_pointfit=new_pointfit(sorted_indexes1o(1:point_num(1)));if point_num(1)>0 && BoomerangFitness(1,i)>new_pointfit(1)Boomerang(i,:)=rd_point(1,:);BoomerangFitness(1,i)=new_pointfit(1);endend%% Update of optimal solution and optimal fitness value% Out-of-bounds processingTp=Boomerang>UB;Tm=Boomerang<LB;Boomerang=(Boomerang.*(~(Tp+Tm)))+UB.*Tp+LB.*Tm;BoomerangFitness=Fobj(Boomerang);[~,sorted_indexes]=sort(BoomerangFitness);Boomerang=Boomerang(sorted_indexes(1:Popsize),:);SortfitbestN = BoomerangFitness(sorted_indexes(1:Popsize));%Update the optimal solutionif SortfitbestN(1)<Best_fitnessBest_position=Boomerang(1,:);Best_fitness=SortfitbestN(1);endConvergence_curve(t)=Best_fitness;t = t + 1;end
end

Shijie Zhao, Fanshuai Meng, Liang Cai, Ronghua Yang,Boomerang Aerodynamic Ellipse Optimizer: A human game-inspired optimization technique for numerical optimization and multilevel thresholding image segmentation,Mathematics and Computers in Simulation,2025,https://doi.org/10.1016/j.matcom.2025.07.006.