机械学习--线性回归---三个小案例
这一节,我将用三个小案例来帮助你详细了解线性回归在python代码中的用法
一、一元线性回归案例
Find商家广告投入和销售额之间关系
数据已经上传,可自行下载
代码 示例:
import pandas as pd
from sklearn.linear_model import LinearRegression
data = pd.read_csv('一元线性回归.csv')
corr = data[['广告投入','销售额']].corr()
lr_model = LinearRegression()
x = data[['广告投入']]
y = data[['销售额']]
lr_model.fit(x,y)
score = lr_model.score(x,y)
print(lr_model.predict([[80]]))
a = lr_model.coef_
b = lr_model.intercept_
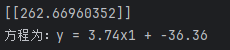
print("方程为:y = {:.2f}x1 + {:.2f}".format(a[0][0],b[0]))讲解:
# 导入pandas库,用于数据处理和分析,通常简写为pd # 从sklearn.linear_model模块导入LinearRegression类,用于创建线性回归模型# 使用pandas的read_csv函数读取CSV文件,将数据存储在DataFrame对象data中 # 这里假设'data(1).csv'文件与当前脚本在同一目录下# 计算'广告投入'和'销售额'两列之间的相关系数 # corr()方法默认计算皮尔逊相关系数,取值范围为[-1, 1],绝对值越接近1表示相关性越强# 创建线性回归模型的实例# 选取'广告投入'作为特征变量(自变量),注意这里使用双括号[[ ]]保持其二维结构 # 选取'销售额'作为目标变量(因变量),同样保持二维结构# 使用特征变量x和目标变量y训练线性回归模型 # 模型会学习x和y之间的线性关系# 计算模型的决定系数R²,评估模型对数据的拟合程度 # R²的取值范围为[0, 1],越接近1表示模型拟合效果越好# 使用训练好的模型预测当广告投入为80时的销售额 # 注意输入需要是二维数组形式[[80]],与训练数据的结构保持一致# 获取线性回归模型的系数(斜率),即方程中的系数a # 获取线性回归模型的截距,即方程中的常数项b# 格式化输出线性回归方程,保留两位小数 # 这里a[0][0]和b[0]是因为coef_和intercept_返回的是数组形式
输出:
二、多元线性回归案例
由体重,年龄的数据推测血管收缩的情况
数据已上传,可自行下载
代码示例:
import pandas as pd
from sklearn.linear_model import LinearRegression
data = pd.read_csv('多元线性回归.csv',encoding='utf-8',engine='python')
corr = data[['体重','年龄','血压收缩']].corr()
lr_model = LinearRegression()
x = data[['体重','年龄']]
y = data[['血压收缩']]
lr_model.fit(x,y)
score = lr_model.score(x,y)
a = lr_model.coef_
b = lr_model.intercept_
print("方程为:y = {:.2f}x1 + {:.2f}x2 + {:.2f}".format(a[0][0],a[0][1],b[0]))
讲解:
# 导入pandas库,用于数据读取和处理,通常简写为pd # 从sklearn的线性模型模块导入LinearRegression类,用于构建多元线性回归模型# 读取CSV文件数据到DataFrame # '多元线性回归.csv'是数据文件名,需与脚本在同一目录或提供完整路径 # encoding='utf-8'指定文件编码为UTF-8,确保中文正常显示 # engine='python'用于处理某些特殊格式的CSV文件,避免解析错误# 计算三个变量之间的相关系数矩阵 # 分析体重、年龄与血压收缩之间的相关性强度 # 相关系数范围[-1,1],绝对值越大表示相关性越强# 创建线性回归模型实例# 确定自变量X:选取'体重'和'年龄'作为特征变量 # 确定因变量y:选取'血压收缩'作为目标变量# 使用训练数据拟合模型,即求解回归方程的系数# 计算模型的决定系数R²,评估模型拟合效果 # R²越接近1,表示模型对数据的解释能力越强# 获取回归系数(斜率),多元回归中会有多个系数 # a是一个二维数组,a[0][0]对应体重的系数,a[0][1]对应年龄的系数 # 获取回归方程的截距项(常数项)# 格式化输出多元线性回归方程 # 方程形式为:y = a1*x1 + a2*x2 + b,其中x1是体重,x2是年龄
输出结果:
![]()
三、超多元线性回归案例
由多项数据分析糖尿病的情况,并对未知数据分析
数据已经上传,可以自行下载
代码示例:
import pandas as pd
from sklearn.linear_model import LinearRegression
data = pd.read_csv('糖尿病数据.csv')
corr = data[['age','sex','bmi','bp','s1','s2','s3','s4','s5','s6','target']].corr()
lr_model = LinearRegression()
x = data[['age','sex','bmi','bp','s1','s2','s3','s4','s5','s6']]
y = data[['target']]
lr_model.fit(x,y)
score = lr_model.score(x,y)
print("准确率为:",score)
print("预测数据:-0.0491050163910452,-0.044641636506989,-0.0568631216082106,-0.0435421881860331,-0.0455994512826475,-0.043275771306016,0.000778807997017968,-0.0394933828740919,-0.0119006848015081,0.0154907301588724")
print("预测结果为:",lr_model.predict([[-0.0491050163910452,-0.044641636506989,-0.0568631216082106,-0.0435421881860331,-0.0455994512826475,-0.043275771306016,0.000778807997017968,-0.0394933828740919,-0.0119006848015081,0.0154907301588724]]))
a = lr_model.coef_
b = lr_model.intercept_
print("方程为:y = {:.2f}x1 + {:.2f}x2 + {:.2f}x3 + {:.2f}x4 + {:.2f}x5 + {:.2f}x6 + {:.2f}x7 + {:.2f}x8 + {:.2f}x9 + {:.2f}x10 + {:.2f}"\.format(a[0][0],a[0][1],a[0][2],a[0][3],a[0][4],a[0][5],a[0][6],a[0][7],a[0][8],a[0][9],b[0]))
讲解:
# 导入pandas库,用于数据读取和处理,简写为pd # 从sklearn线性模型模块导入LinearRegression类,用于构建线性回归模型# 读取糖尿病数据集CSV文件 # 假设'diabetes_data.csv'与当前脚本在同一目录下# 计算多个变量之间的相关系数矩阵 # 分析age(年龄)、sex(性别)、bmi(体重指数)、bp(血压)等特征与target(目标变量)的相关性# 创建线性回归模型实例# 确定自变量X:选取多个特征变量作为输入 # 包括age(年龄)、sex(性别)、bmi(体重指数)、bp(血压)及s1-s6等医学指标 # 确定因变量y:选取target作为预测目标(通常是糖尿病进展指标)# 使用特征变量和目标变量训练模型,拟合线性回归方程# 计算模型的决定系数R²,评估模型拟合效果 # R²越接近1,表示模型对数据的解释能力越强# 打印用于预测的输入数据# 使用训练好的模型对给定数据进行预测 # 输入数据需与训练时的特征顺序一致,且为二维数组形式# 获取回归系数(每个特征对应的权重) # a是一个二维数组,a[0][i]对应第i+1个特征的系数 # 获取回归方程的截距项(常数项)# 格式化输出多元线性回归方程,保留两位小数 # 方程形式为:y = w1*x1 + w2*x2 + ... + w10*x10 + b
输出结果:

四、思路总结
对于线性回归的代码,不管是几元的数据,编程思路都一样
- 数据准备:均使用
pandas的read_csv函数读取 CSV 格式的数据集,获取分析所需的原始数据。(不同的数据集修改读取的cv2函数就行) - 相关性分析:通过
corr()方法计算关注变量(特征与目标变量)之间的相关系数,初步了解变量间的关联程度。(这一步是必须的低于80%的数据集就不适合用线性回归了) - 模型构建与训练:
- 实例化
LinearRegression类创建线性回归模型。 - 确定自变量(特征变量)和因变量(目标变量),从数据中选取对应列。
- 调用
fit()方法,用选定的自变量和因变量训练模型,使模型学习变量间的线性关系。
- 实例化
- 模型评估与应用:
- 用
score()方法获取决定系数 R²,评估模型对数据的拟合效果。 - 提取模型的系数(特征权重)和截距,得到回归方程,量化各特征对目标变量的影响。
- 可通过
predict()方法,利用训练好的模型对新数据进行预测(前两个代码未展示预测,第三个代码有具体预测示例)。
- 用
