算法训练营day34 动态规划② 62.不同路径、63. 不同路径 II、343整数拆分、96.不同的二叉搜索树

        动态规划的第二篇博客！进阶题目，有一说一，尤其最后一道题，真的难想到这种解法

        找规律！！！

62.不同路径

        注意本题是路径不是路程！！！

动态规划

• 确定dp数组（dp table）以及下标的含义

        dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

• 确定递推公式

        想要求dp[i][j]，只能有两个方向来推导出来，即dp[i - 1][j] 和 dp[i][j - 1]。

        那么很自然，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，因为dp[i][j]只有这两个方向过来。

• dp数组的初始化

        dp[i][0]一定都是1，因为从(0, 0)的位置到(i, 0)的路径只有一条，那么dp[0][j]也同理

• 确定遍历顺序

        这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，dp[i][j]都是从其上方和左方推导而来，那么从左到右一层一层遍历就可以了。

        这样就可以保证推导dp[i][j]的时候，dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。

• 举例推导dp数组（后续略）

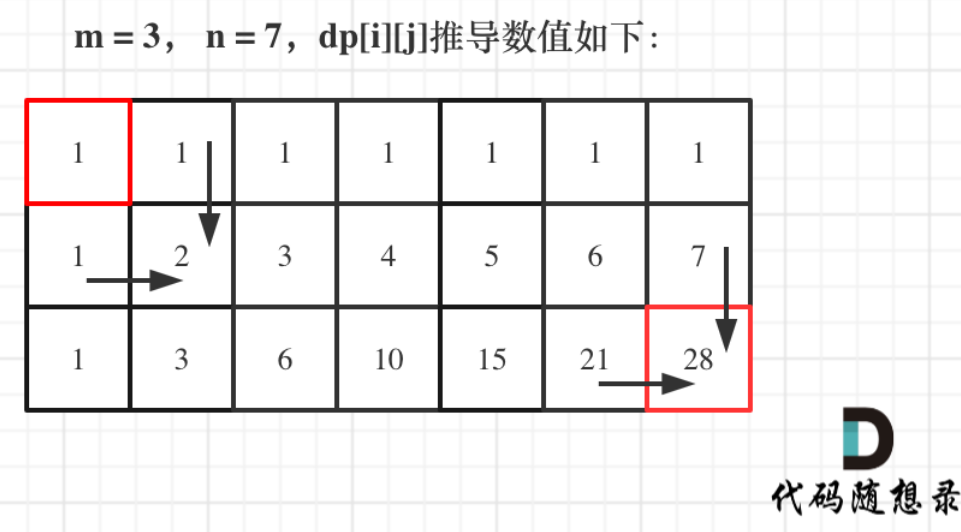
class Solution:def uniquePaths(self, m: int, n: int) -> int:dp = [[0] * n for _ in range(m)]for i in range(m):dp[i][0] = 1for j in range(n):dp[0][j] = 1for i in range(1, m):for j in range(1, n):dp[i][j] = dp[i - 1][j] + dp[i][j - 1] # 核心逻辑, 路径数为上节点数 + 左节点数return dp[m - 1][n - 1]'''
# 空间优化
# 仅留最后一行数据, 其他行数据用于过程计算
class Solution:def uniquePaths(self, m: int, n: int) -> int:# 创建一个一维列表用于存储每列的唯一路径数dp = [1] * n# 计算每个单元格的唯一路径数for j in range(1, m):for i in range(1, n):dp[i] += dp[i - 1]# 返回右下角单元格的唯一路径数return dp[n - 1]
'''

数论

        在这个图中，可以看出一共m，n的话，无论怎么走，走到终点都需要 m + n - 2 步。在这m + n - 2 步中，一定有 m - 1 步是要向下走的，不用管什么时候向下走。

        那么有几种走法呢？ 可以转化为，给你m + n - 2个不同的数，随便取m - 1个数，有几种取法。那么这就是一个组合问题了。

class Solution:def uniquePaths(self, m: int, n: int) -> int:# 核心是一个组合算法的实现numerator = 1  # 分子denominator = m - 1  # 分母count = m - 1  # 计数器，表示剩余需要计算的乘积项个数t = m + n - 2  # 初始乘积项while count > 0:numerator *= t  # 计算乘积项的分子部分t -= 1  # 递减乘积项while denominator != 0 and numerator % denominator == 0:numerator //= denominator  # 约简分子denominator -= 1  # 递减分母count -= 1  # 计数器减1，继续下一项的计算return numerator  # 返回最终的唯一路径数

深度搜索

        题目中说机器人每次只能向下或者向右移动一步，那么其实机器人走过的路径可以抽象为一棵二叉树，而叶子节点就是终点！

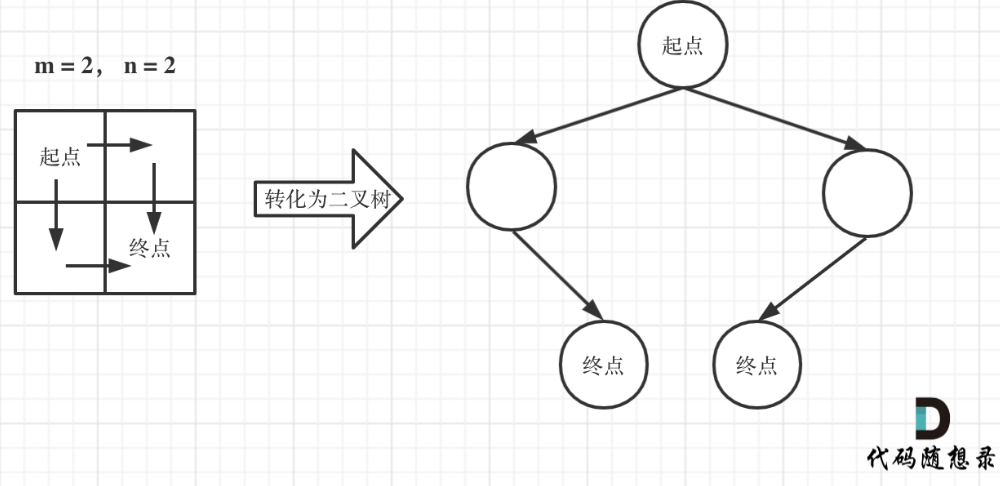
        最后来看这个代码就很简单了

class Solution:def uniquePaths(self, m: int, n: int) -> int:if m == 1 or n == 1:return 1return self.uniquePaths(m - 1, n) + self.uniquePaths(m, n - 1)

63. 不同路径 II

        相对上题增加了障碍，有障碍的话，其实就是标记对应的dp table（dp数组）保持初始值(0)就可以了。

• 确定dp数组（dp table）以及下标的含义

        dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

• 确定递推公式

        递推公式和上题一样，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。

        但这里需要注意一点，因为有了障碍，(i, j)如果就是障碍的话应该就保持初始状态（初始状态为0）。

• dp数组如何初始化

        因为从(0, 0)的位置到(i, 0)的路径只有一条，所以dp[i][0]一定为1，dp[0][j]也同理。

        但如果(i, 0) 这条边有了障碍之后，障碍之后（包括障碍）都是走不到的位置了，所以障碍之后的dp[i][0]应该还是初始值0。

• 确定遍历顺序

        从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 中可以看出，一定是从左到右一层一层遍历，这样保证推导dp[i][j]的时候，dp[i - 1][j] 和 dp[i][j - 1]一定是有数值。

class Solution:def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:m = len(obstacleGrid)n = len(obstacleGrid[0])if obstacleGrid[m - 1][n - 1] == 1 or obstacleGrid[0][0] == 1:return 0# 终点和起点有阻碍dp = [[0] * n for _ in range(m)]for i in range(m):if obstacleGrid[i][0] == 0:dp[i][0] = 1else:breakfor j in range(n):if obstacleGrid[0][j] == 0:dp[0][j] = 1else:breakfor i in range(1, m):for j in range(1, n):if obstacleGrid[i][j] == 1:continuedp[i][j] = dp[i - 1][j] + dp[i][j - 1]return dp[m - 1][n - 1]

343整数拆分

• 确定dp数组（dp table）以及下标的含义

        dp[i]：分拆数字i，可以得到的最大乘积为dp[i]。

• 确定递推公式

        从1遍历j，有两种渠道得到dp[i].

1. 一个是j * (i - j) 直接相乘。（拆分为两个数）
2. 一个是j * dp[i - j]，相当于是拆分(i - j) （拆分为3个及3个以上的数）

        所以递推公式：dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});在递推公式推导的过程中，增加参数dp[i]，取最大。

• dp的初始化

        dp[0] dp[1] 不应该初始化，只初始化dp[2] = 1

• 确定遍历顺序

        dp[i] 是依靠 dp[i - j]的状态，所以遍历i一定是从前向后遍历，先有dp[i - j]再有dp[i]。

class Solution:def integerBreak(self, n: int) -> int:# 假设对正整数 i 拆分出的第一个正整数是 j（1 <= j < i），则有以下两种方案：# 1) 将 i 拆分成 j 和 i−j 的和，且 i−j 不再拆分成多个正整数，此时的乘积是 j * (i-j)# 2) 将 i 拆分成 j 和 i−j 的和，且 i−j 继续拆分成多个正整数，此时的乘积是 j * dp[i-j]dp = [0] * (n + 1)dp[2] = 1for i in range(3, n + 1):# 开始计算具体的dp[i]for j in range(1, i // 2 + 1):dp[i] = max(dp[i], (i - j) * j, dp[i - j] * j)return dp[n]

96.不同的二叉搜索树 

很明显的动态规划题目，但是递推公式确实很难想到

• 确定dp数组（dp table）以及下标的含义

        dp[i] ： 1到i为节点组成的二叉搜索树的个数为dp[i]。

• 确定递推公式

        在上面的分析中，其实已经看出其递推关系， dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]

        j相当于是头结点的元素，从1遍历到i为止。eg3: 2.0 + 1.1 + 0.2 

• dp数组如何初始化

        初始化dp[0] = 1

• 确定遍历顺序

        节点数为i的状态是依靠 i之前节点数的状态。所以我认为仍然可以理解为自前向后遍历

class Solution:def numTrees(self, n: int) -> int:dp = [0] * (n + 1)dp[0] = 1for i in range(1, n + 1):for j in range(1, i + 1):dp[i] += dp[j - 1] * dp[i - j]return dp[n]