当前位置：首页 > news >正文

数据结构-排序（2）

news 2025/8/12 11:44:00

一、堆排序（借助树）

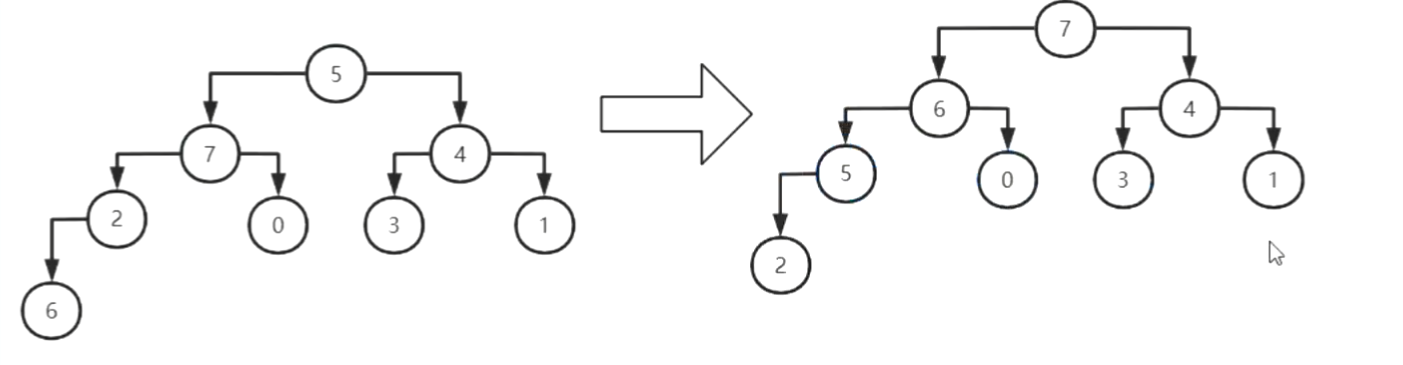
1.利用完全二叉树构建大顶堆
2.堆顶元素和堆底元素进行交换，堆底元素不再参与构建，剩余元素继续构建大顶堆
3.时间复杂度 O(nlogn)

1.完全二叉树：按照从上到下，从左到右的顺序进行排序

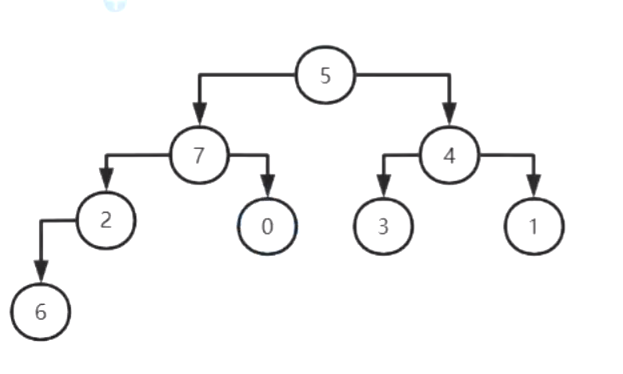
2.大顶堆：任何一个节点值大于等于左右孩子，根节点一定是最大值

arr[i]的左孩子 arr[2i+1] 要求条件： arr[i]>= arr[2i+1]&&
arr[i]的右孩子 arr[2i-2] arr[i]>=arr[2i-2]

3.构建大顶堆:

第一大步：

1. 从后往前对每个数据依次进行检测调整
2. 定义 parent 游标指向要检测的节点
3. 定义 parent 的左孩子，判断 child 是否为空（有孩子一定会有左孩子）
4. 如果 child 为空，则 parent 符合大顶堆
5. 如果 child 不为空，判断 parent 有没有右孩子，child 指向左右孩子的最大值。
6. 父子节点进行比较，如果父节点的值大，则符合大顶堆，继续向前检测。
7. 如果父节点的值小，则不符合大顶堆，父子节点进行交换。
8. parent 指向 child, child 指向左右孩子的最大值。直到 child 为空或者父节点的值大。

第二大步：

1.只有堆顶变了，只维护堆顶就可以，做到堆顶最大

package com.pcby.demo;//堆排序
import java.util.Arrays;
/*1.利用完全二叉树构建大顶堆* 2.堆顶元素和堆底元素进行交换，堆底元素不再参与构建，剩余元素继续构建大顶堆*/public class HeapSort {public static void main(String[] args) {int[] arr= {5,7,4,2,0,3,1,6};sort(arr);System.out.println(Arrays.toString(arr));}// 排序public static void sort(int[] arr){// 第一大步for (int i = arr.length - 1; i >= 0; i--) {adjust(arr, i, arr.length);}// 第二大步for (int i = arr.length - 1; i >= 0; i--) {int temp = arr[0];arr[0] = arr[i];arr[i] = temp;adjust(arr, 0, i);}}// 维护public static void adjust(int[] arr, int parent, int length) {int child = 2 * parent + 1;while (child < length) {// 定义右孩子int rchild = child + 1;if (rchild < length && arr[rchild] > arr[child]) {child++;} // child 指向了左右孩子的最大值// 父子节点进行比较，父节点要大if (arr[parent] < arr[child]) {// 父子节点进行交换int temp = arr[parent];arr[parent] = arr[child];arr[child] = temp;// 父节点指向 child, child 指向左右孩子最大值parent = child;child = 2 * child + 1;} else {break;}}}
}

每一步思路：
1. 定义数组并调用排序函数：
在 main 方法中，定义一个数组 arr ，其元素为 {5,7,4,2,0,3,1,6} 。
调用 sort 方法对数组进行堆排序。
输出排序后的数组。
2. 排序方法（sort 方法）：
第一大步（构建初始大顶堆）：
从数组的最后一个元素开始，逐个向前调整，确保每个父节点都大于其子节点。
调用 adjust 方法对每个元素进行调整。
第二大步（排序过程）：
将堆顶元素（最大值）与堆底元素交换，使最大值位于数组末尾。
堆的大小减 1（通过调整 length 参数实现），对剩余元素重新调整为大顶堆。
重复上述交换和调整过程，直到堆的大小为 1。
3. 调整堆结构（adjust 方法）：
初始化父节点和左孩子节点的位置。
在循环中，检查右孩子节点是否存在且是否大于左孩子节点，将 child 指向左右孩子中较大的那个。
如果父节点小于当前 child 节点，交换它们的位置。
更新父节点和孩子节点的位置，继续调整子树，直到父节点大于等于孩子节点或孩子节点超出堆的范围。

二、基数排序（借助桶）

不能排负值，先排序个位，十位，百位

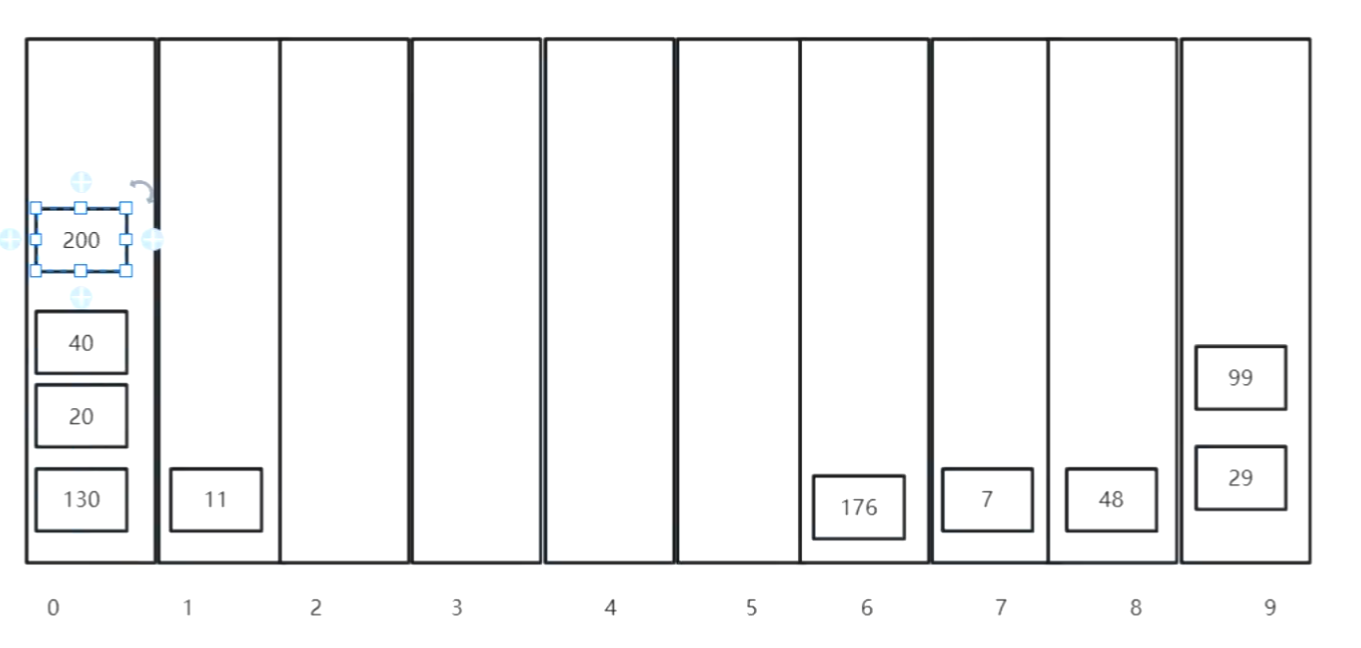
1.先建立0-9九个桶

2.看各个数字个位数都是多少，是多少放在哪个桶里

3.放好后从0号桶开始取数字，取出来，在排序十位，同理排序百位

 
package com.pcby.demo;import java.util.Arrays;public class Radix {public static void main(String[] args) {int[] arr = {5,14,20,125,362,61,94,4,12,1002,54,99,87,89};sort(arr);System.out.println(Arrays.toString(arr));}public static void sort(int[] arr) {// 找最大值int max = arr[0];for (int i = 0; i < arr.length; i++) {if (arr[i] > max) {max = arr[i];}}// 最大值的位数int len = (max + "").length();// 声明 0-9 十个桶int[][] bucket = new int[10][arr.length];// 桶记录工具int[] elementCount = new int[10];int n = 1;// 循环放入取出for (int num = 0; num < len; num++) {// 放入for (int i = 0; i < arr.length; i++) {// 放到哪个桶 余数int element = arr[i] / n % 10;int count = elementCount[element];bucket[element][count] = arr[i];// 桶记录 +1elementCount[element]++;}// 取出int index = 0;for (int i = 0; i < elementCount.length; i++) {if (elementCount[i] > 0) {for (int j = 0; j < elementCount[i]; j++) {arr[index] = bucket[i][j];index++;}elementCount[i] = 0;}}n = n * 10;}}
}

三、快速排序

待排序数组的第一个作为基准数；
定义游标 j 从后往前，找比基准数小的值，找到后停下；
定义游标 i 从前往后，找比基准数大的值，找到后停下；
i j 指向的数据交换 j 继续找比基准数小的，i 继续找比基准数大的，直到 i j 相遇基准数和相遇位置交换，基准数到达正确位置；
以基准数为起始点，拆分成左右两部分，重复上述所有，直到数据独立
时间复杂度： O(n log n)

import java.util.Arrays;public class QuickSort {public static void main(String[] args) {int[] arr = {5, 7, 4, 2, 0, 3, 1, 6};sort(arr, 0, arr.length - 1);System.out.println(Arrays.toString(arr));}public static void sort(int[] arr, int left, int right) {if (left >= right) {return;}int base = arr[left];int j = right;int i = left;while (i != j) {while (arr[j] >= base && i != j) {j--;}while (arr[i] <= base && i != j) {i++;}int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}arr[left] = arr[i];arr[i] = base;sort(arr, left, i - 1);sort(arr, i + 1, right);}
}

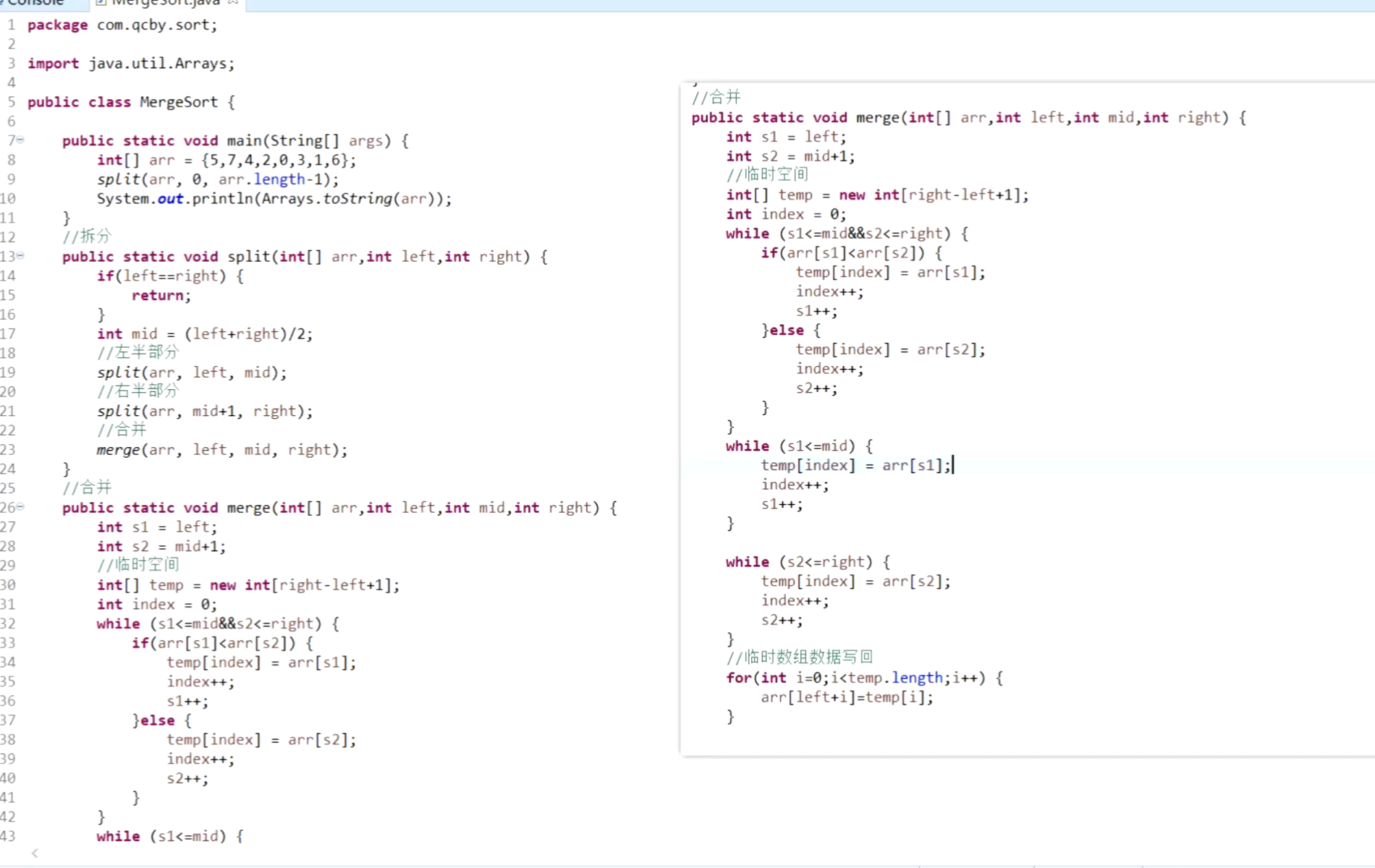
四、归并排序

即将数组不断拆分为小数组，对小数组进行排序后再合并成大数组。先拆分再合并，在合并的过程中通过临时空间进行排序。
空间复杂度：O(n)


package com.qcbj.sort;
import java.util.Arrays;public class MergeSort {public static void main(String[] args) {int[] arr = {5, 7, 4, 2, 0, 3, 1, 6};split(arr, 0, arr.length - 1);System.out.println(Arrays.toString(arr));}public static void split(int[] arr, int left, int right) {if (left == right) {return;}int mid = (left + right) / 2;split(arr, left, mid);split(arr, mid + 1, right);merge(arr, left, mid, right);}public static void merge(int[] arr, int left, int mid, int right) {int s1 = left;int s2 = mid + 1;int[] temp = new int[right - left + 1];int index = 0;while (s1 <= mid && s2 <= right) {if (arr[s1] <= arr[s2]) {temp[index] = arr[s1];index++;s1++;} else {temp[index] = arr[s2];index++;s2++;}}while (s1 <= mid) {temp[index] = arr[s1];index++;s1++;}while (s2 <= right) {temp[index] = arr[s2];index++;s2++;}for (int i = 0; i < temp.length; i++) {arr[left + i] = temp[i];}}
}