当前位置：首页 > news >正文

【排序算法】⑦归并排序

news 2025/8/12 11:43:58

系列文章目录

第一篇：【排序算法】①直接插入排序-CSDN博客

第二篇：【排序算法】②希尔排序-CSDN博客

第三篇：【排序算法】③直接选择排序-CSDN博客

第四篇：【排序算法】④堆排序-CSDN博客

第五篇：【排序算法】⑤冒泡排序-CSDN博客

第六篇：【排序算法】⑥快速排序：Hoare、挖坑法、前后指针法-CSDN博客

第七篇：【排序算法】⑦归并排序-CSDN博客

文章目录

目录

系列文章目录

文章目录

前言

一、什么是归并排序？

算法思想

举个例子

具体步骤

二、实现归并排序

MergeSort函数

_MergeSort函数

递归式分解数组

合并子序列

图解

完整归并排序代码

四、分析归并排序

总结

前言

归并排序，是一种基于分治策略的排序算法。

它的基本思想是将一个大问题分解成若干个小问题，分别解决小问题，然后将解决的小问题合并起来得到大问题的解。

递归排序有递归版本和非递归版本，本文用递归版介绍归并排序。

一、什么是归并排序？

算法思想

归并排序，是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。

归并排序的主要步骤包括“分”和“治”两个阶段：

分——把一个困难的大问题分成若干小问题，小问题再分成小小问题，直到不能再分；

治——依次解决小小问题，几个小小问题解决了等同于解决了一个小问题；几个小问题解决了等同于解决了这个困难的大问题。

举个例子

1.分：将整副牌分成两半，然后分别将这两半再分成四半，直到每一份只剩下一张牌（一张牌自然是有序的）。

2. 治：将两个有序的小份合并成一个有序的大份。合并时，就像你有两堆已经按顺序排好的牌，每次从两堆牌顶选出较小的一张，按扑克牌大小依次放到新堆中，直到两堆牌都取完。

具体步骤

1. 分解：将当前数组一分为二（即从中间分成两个子数组）。

2. 递归：递归地对两个子数组进行分解（直到子数组长度为1，则自然有序）。

3. 合并：将两个单数据的子数组合并成一个有序数组；有序数组再合并成有序数组，直到整个大数组有序。

二、实现归并排序

MergeSort函数

由于需要不断的进行递归式的分解数组，所以在原数组上操作是不方便的，于是我们在MergeSort函数中malloc出一个空间用于相关操作。

所以代码得出：

void MergeSort(int* a, int n)
{if (!a)return;//这就是为什么要创建_MergeSort的原因int* temp = (int*)malloc(sizeof(int) * n);if (!temp)return;_MergeSort(a, 0, n - 1, temp);free(temp);temp = NULL;
}

既然MergeSort函数中存在申请空间的行为，自然是不适合进行递归式操作的，所以额外定义一个_MergeSort函数用于进行递归分数组和子数组合并。

_MergeSort函数

_MergeSort函数用于进行递归分数组和子数组合并。

递归式分解数组

这在本系列之前的排序中（如快速排序）就已经接触过了，操作分几步：

①获取数组中点
int div= left + (right - left) / 2;
注意：不能写int div= (right - left) / 2，因为还需要在分数组中继续分，所以应该求得是每段段区间的中点，而不是整个大区间数组的中点。

②递归分数组

将mid分成的两个区间[left,mid),[mid+1,right]分别递归式传入_MergeSort函数即可。
_MergeSort(a, left, div, t);
_MergeSort(a, div+ 1, right, t);
所以函数至少需要四个形参：传原数组；传分数组的的左端；传分数组的的右端；在MergeSort中申请出来的空间地址。

什么时候终止？当分解成单个元素时即可终止。
if (left >= right)return;

当准备工作做好后，就到了合并阶段了。

合并子序列

尽管不知道是哪个子序列，但函数形参中有该区间的左端点和右端点，因此也能遍历该子区间。

再回顾上述扑克牌合并的例子：“合并时，就像你有两堆已经按顺序排好的牌，每次从两堆牌中选出较小的一张，按扑克牌大小依次放到新堆中，直到两堆牌都取完。”

同理，由于不知道两个子序列谁大谁小，所以需要将它们一个一个比较后再放入申请出来的空间中：

int begin1 = left, end1 = div;
int begin2 = div + 1, end2 = right;int end = left;

解释：
①当递归式分解数组到单个数据后，一定通过 if 条件返回接着执行升序的代码，所以直接用上述div分隔开的两个子序列合并即可。

②end用于记录该段区间的首元素在大数组中的下标，方便存放在malloc出的相同空间的相同数组下标。

核心代码

	while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){t[end++] = a[begin1++];}else{t[end++] = a[begin2++];}}//由于不确定上述循环结束后，哪个区间还有数据：while (begin1 <= end1){t[end++] = a[begin1++];}while (begin2 <= end2){t[end++] = a[begin2++];}memcpy(a + left, t + left, sizeof(int) * (right - left + 1));

解释：

①由于不知道两个子序列谁大谁小，所以在循环中一个一个比较，小的先放在申请出来的t空间中；

②第一个循环结束后，由于不知道是哪个区间先结束的，哪个区间还有剩，所以两个区间一起尝试。有剩余的区间会满足循环判断条件进入循环。

③当一个两个区间合并完后立即通过memcpy函数复制回原数组。

图解

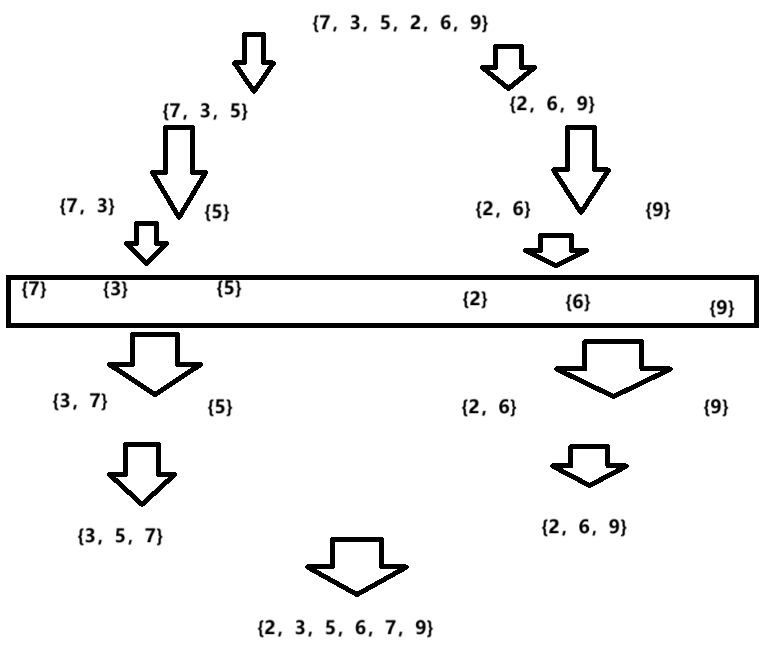
完整归并排序代码

综合上述代码，可得出归并排序完整代码：

#include<stdio.h>
#include<stdlib.h>
#include<string.h>//递归归并
void MergeSort(int* a, int a_size)
{if (!a)return;//这就是为什么要创建_MergeSort的原因int* temp = (int*)malloc(sizeof(int) * a_size);if (!temp)return;_MergeSort(a, 0, a_size- 1, temp);free(temp);temp = NULL;
}void _MergeSort(int* a, int left, int right, int* t)
{if (left >= right)return;int div = left + (right - left) / 2;_MergeSort(a, left, div, t);_MergeSort(a, div + 1, right, t);int begin1 = left, end1 = div;int begin2 = div + 1, end2 = right;int end = left;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){t[end++] = a[begin1++];}else{t[end++] = a[begin2++];}}//由于不确定上述循环结束后，哪个区间还有数据：while (begin1 <= end1){t[end++] = a[begin1++];}while (begin2 <= end2){t[end++] = a[begin2++];}memcpy(a + left, t + left, sizeof(int) * (right - left + 1));
}