当前位置： 首页 > news >正文

数据结构：栈和队列(Stack Queue)基本概念与应用

news 2025/8/11 9:35:03

栈与队列：从基础到实现与应用

栈和队列是计算机科学中最基础且重要的两种数据结构，它们都属于线性表，但在操作方式上有着显著差异。

本文主要有三个内容

  • 知识点一：介绍栈和队列的基本概念
  • 知识点二：栈和队列基本代码使用方法
  • 知识点三：学习使用栈和队列进行后缀表达式求值（来源：牛客网；难度：较难）
  • 查看：每日一题：使用栈实现逆波兰表达式求值
    在这里插入图片描述

文章目录

  • 栈与队列：从基础到实现与应用
    • 本文主要有三个内容
    • 一、栈与队列的基本概念
      • 1.1 栈：后进先出(LIFO)结构
      • 1.2 队列：先进先出(FIFO)结构
    • 二、栈与队列的实现方式
      • 2.1 栈的实现
        • 2.1.1 顺序栈(数组实现)
        • 2.2.2 链式栈(链表实现)
      • 2.2 队列的实现
        • 2.2.1 循环队列(数组实现)
        • 2.2.2 链式队列(链表实现)
    • 三、栈与队列的相互实现（简要介绍）
      • 3.1 用栈实现队列
      • 3.2 用队列实现栈
    • 四、栈与队列的应用场景
      • 4.1 栈的应用
      • 4.2 队列的应用
    • 五、栈与队列的扩展知识
      • 5.1 共享栈
      • 5.2 双端队列(Deque)
      • 5.3 优先队列(Priority Queue)
    • 六、总结

一、栈与队列的基本概念

1.1 栈：后进先出(LIFO)结构

栈(Stack)是一种限定仅在表尾进行插入和删除操作的线性表，遵循后进先出(Last In First Out, LIFO)的原则。栈的基本操作包括：

  • 入栈(Push)：在栈顶添加一个元素
  • 出栈(Pop)：移除并返回栈顶元素
  • 查看栈顶(Peek/Top)：返回栈顶元素但不移除
  • 判空(IsEmpty)：检查栈是否为空
  • 获取大小(Size)：返回栈中元素数量
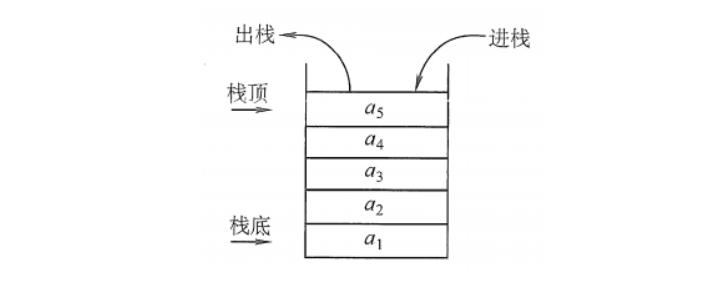
  • 在这里插入图片描述

栈的典型类比是摞盘子——你只能从最上面取放盘子，最后放上去的盘子最先被取走。

1.2 队列：先进先出(FIFO)结构

队列(Queue)是一种限定在表的前端(队头)进行删除操作，在表的后端(队尾)进行插入操作的线性表，遵循先进先出(First In First Out, FIFO)的原则。队列的基本操作包括：

  • 入队(Enqueue)：在队尾添加一个元素
  • 出队(Dequeue)：移除并返回队头元素
  • 查看队头(Front)：返回队头元素但不移除
  • 判空(IsEmpty)：检查队列是否为空
  • 获取大小(Size)：返回队列中元素数量

队列的现实类比是排队——先来的人先获得服务，后来的人排在队尾。

二、栈与队列的实现方式

2.1 栈的实现

栈可以通过顺序存储结构(数组)或链式存储结构(链表)来实现。

2.1.1 顺序栈(数组实现)

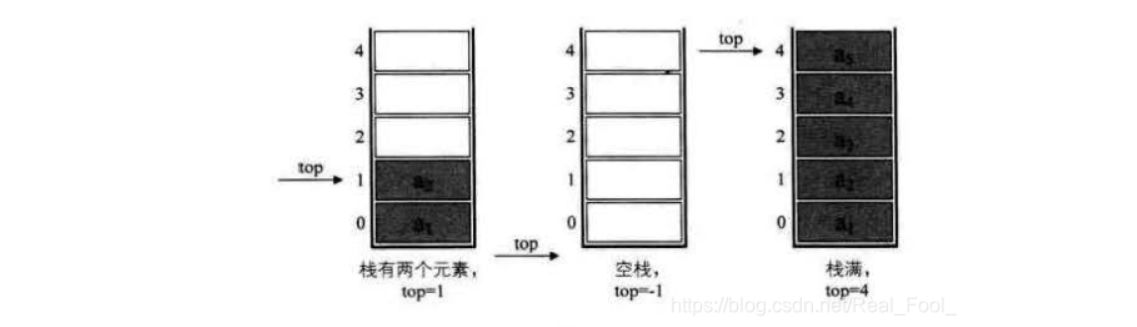
采用顺序存储的栈称为顺序栈，它利用一组地址连续的存储单元存放自栈底到栈顶的数据元素，同时附设一个指针（top）指示当前栈顶元素的位置。
若存储栈的长度为StackSize，则栈顶位置top必须小于StackSize。当栈存在一个元素时，top等于0，因此通常把空栈的判断条件定位top等于-1。
在这里插入图片描述

#define MAX_SIZE 100typedef struct {int data[MAX_SIZE];int top; // 栈顶指针
} SeqStack;// 初始化栈
void InitStack(SeqStack *S) {S->top = -1;         // 初始时候为-1
}// 入栈
void Push(SeqStack *S, int value) {     // value是你需要push的值if (S->top >= MAX_SIZE - 1) {printf("栈满\n");         // 这里采用的牺牲一个存储空间的方式return;}S->data[++S->top] = value;      // ++S.top应该是S.top+1； 和S.top++不同，写的比较绕。
}// 出栈
int Pop(SeqStack *S) {if (S->top == -1) {printf("栈空\n");return -1;}return S->data[S->top--];     // 第一个数据的指针是-1，最后一个数据的指针是top -1？实则不然// top -- 是先取出top再对top -1，当top大于0时，才存在数据。
}// 查看栈顶
int Peek(SeqStack *S) {if (S->top == -1) {printf("栈空\n");return -1;}return S->data[S->top];
}
2.2.2 链式栈(链表实现)

采用链式存储的栈称为链栈，链栈的优点是便于多个栈共享存储空间和提高其效率，且不存在栈满上溢的情况。通常采用单链表实现，并规定所有操作都是在单链表的表头进行的。这里规定链栈没有头节点，Lhead指向栈顶元素，如下图所示。

在这里插入图片描述

typedef struct StackNode {int data;struct StackNode *next;
} StackNode;typedef struct {StackNode *top; // 栈顶指针int size;       // 栈大小
} LinkedStack;// 初始化栈
void InitStack(LinkedStack *S) {S->top = NULL;S->size = 0;
}// 入栈
void Push(LinkedStack *S, int value) {StackNode *newNode = (StackNode*)malloc(sizeof(StackNode));      // 先生成一个节点并赋值newNode->data = value;           // 这里赋值newNode->next = S->top;          // 接下来这两句比较难理解，看图  S->top = newNode;                // 这时候才真正加入newNode，之前只是为了将已有的节点加到NewNode上面S->size++;
}// 出栈
int Pop(LinkedStack *S) {if (S->top == NULL) {printf("栈空\n");return -1;}StackNode *temp = S->top;int value = temp->data;     // 需要返回的值S->top = S->top->next;      // 这个就是将TOP指针移到第二个元素（倒数第二个进来的元素）free(temp);                 // 这个函数free() 是一个非常重要的内存管理函数temp 是原栈顶节点，在 Pop 后它不再属于栈的一部分。// 如果不 free(temp)，会导致 内存泄漏（Memory Leak），即这块内存无法再被程序使用，但系统也无法回收它。S->size--;return value;              // 这就是你所需要的值 int val1 = Pop(&stack);  // 弹出最后一个元素
}

入栈注意

  	newNode->next = S->top;          // 接下来这两句比较难理解，看图  S->top = newNode;                // 这时候才真正加入newNode，之前只是为了将已有的节点加到NewNode上面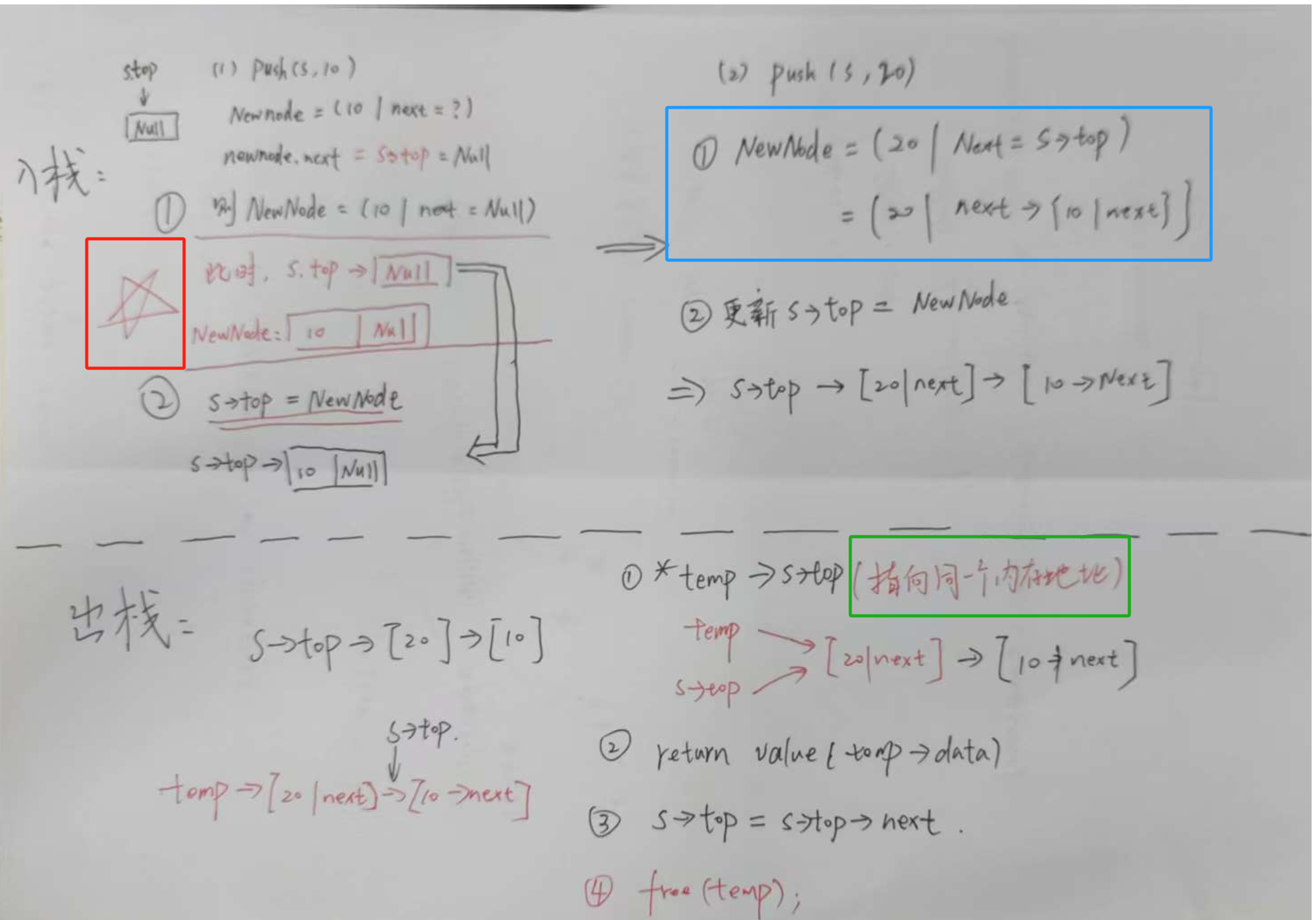

在这里插入图片描述

2.2 队列的实现

队列（queue）是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。
队列同样可以通过顺序存储或链式存储实现，顺序队列需要考虑循环队列以解决"假溢出"问题。
在这里插入图片描述

  • 初始状态（队空条件）：Q->front == Q->rear == 0。
  • 进队操作：队不满时，先送值到队尾元素，再将队尾指针加1。
  • 出队操作：队不空时，先取队头元素值，再将队头指针加1。
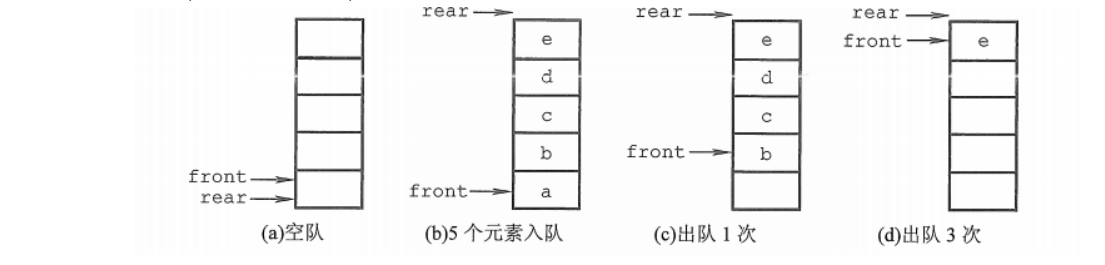
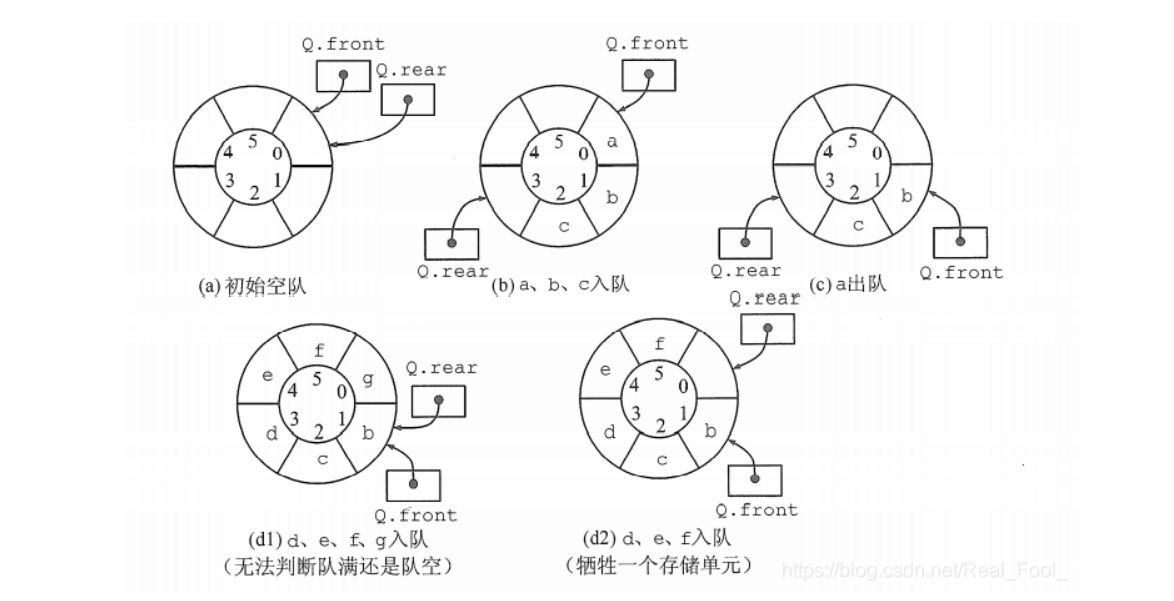
    在这里插入图片描述
    如图d，队列出现“上溢出”，然而却又不是真正的溢出，所以是一种“假溢出”。
2.2.1 循环队列(数组实现)
  • 队空的条件是 Q->front == Q->rear 。
  • 若入队元素的速度快于出队元素的速度，则队尾指针很快就会赶上队首指针，如图( d1 ）所示，此时可以看出队满时也有 Q ->front == Q -> rear 。
  • （1）牺牲一个单元来区分队空和队满，入队时少用一个队列单元，这是种较为普遍的做法，约定以“队头指针在队尾指针的下一位置作为队满的标志” 。队满条件： (Q->rear + 1)%Maxsize == Q->front
  • （2）类型中增设tag 数据成员，以区分是队满还是队空。tag 等于0时，若因删除导致 Q->front == Q->rear ，则为队空；tag 等于 1 时，若因插入导致 Q ->front == Q->rear ，则为队满。
  • （3）类型中增设表示元素个数的数据成员。这样，队空的条件为 Q->size == O ；队满的条件为 Q->size == Maxsize 。这两种情况都有 Q->front == Q->rear

在这里插入图片描述

#define MAX_SIZE 100typedef struct {int data[MAX_SIZE];int front; // 队头指针int rear;  // 队尾指针
} CircularQueue;// 初始化队列
void InitQueue(CircularQueue *Q) {Q->front = Q->rear = 0;
}// 入队
void Enqueue(CircularQueue *Q, int value) {if ((Q->rear + 1) % MAX_SIZE == Q->front) {printf("队列满\n");return;}Q->data[Q->rear] = value;Q->rear = (Q->rear + 1) % MAX_SIZE;
}// 出队
int Dequeue(CircularQueue *Q) {if (Q->front == Q->rear) {printf("队列空\n");return -1;}int value = Q->data[Q->front];Q->front = (Q->front + 1) % MAX_SIZE;  // 更新front索引值return value;
}
2.2.2 链式队列(链表实现)

初始化链表front和rear都指向空节点，队列的链式存储结构表示为链队列，实际上是一个同时带有队头指针和队尾指针的单链表，只能尾进头出。
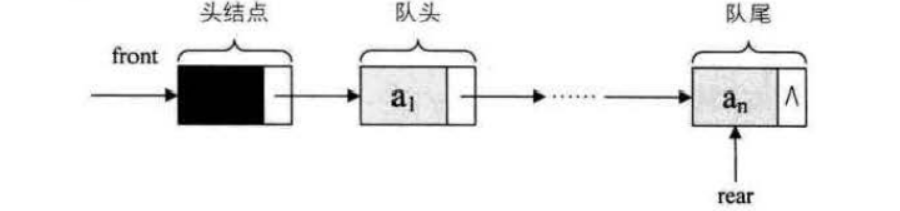
在这里插入图片描述
链队列入队
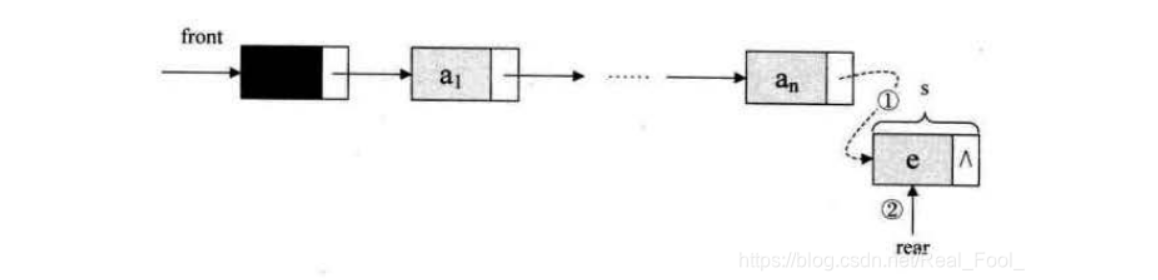
在这里插入图片描述

链队列出队:出队操作时，就是头结点的后继结点出队，将头结点的后继改为它后面的结点，若链表除头结点外只剩一个元素时，则需将rear指向头结点。
在这里插入图片描述

typedef struct QueueNode {int data;struct QueueNode *next;
} QueueNode;typedef struct {QueueNode *front; // 队头指针QueueNode *rear;  // 队尾指针int size;         // 队列大小
} LinkedQueue;// 初始化队列
void InitQueue(LinkedQueue *Q) {Q->front = Q->rear = NULL;Q->size = 0;
}// 入队
void Enqueue(LinkedQueue *Q, int value) {QueueNode *newNode = (QueueNode*)malloc(sizeof(QueueNode));newNode->data = value;newNode->next = NULL;if (Q->rear == NULL) {Q->front = Q->rear = newNode;} else {Q->rear->next = newNode;Q->rear = newNode;}Q->size++;
}// 出队
int Dequeue(LinkedQueue *Q) {if (Q->front == NULL) {printf("队列空\n");return -1;}QueueNode *temp = Q->front;int value = temp->data;Q->front = Q->front->next;if (Q->front == NULL) {Q->rear = NULL;   // 若链表除头结点外只剩一个元素时，则需将rear指向头结点}free(temp);Q->size--;return value;
}

在队列的链式实现中，Q->front 是一个指针，它指向队列的第一个元素（队头）。更进一步理解它的结构以及插入元素时的赋值过程。

1. 链式队列的结构
假设我们有一个链式队列 Q，初始状态为空：

typedef struct QueueNode {int data;               // 数据域struct QueueNode *next; // 指针域，指向下一个节点
} QueueNode;typedef struct {QueueNode *front; // 队头指针（指向第一个节点）QueueNode *rear;  // 队尾指针（指向最后一个节点）
} LinkedQueue;

初始时：

Q->front = NULL
Q->rear  = NULL

队列结构：

Q: { front -> NULL, rear -> NULL }

2. 插入第一个元素（Enqueue）
假设我们要插入 10：

Enqueue(Q, 10);

步骤分析：

  1. 创建新节点：

    QueueNode *newNode = (QueueNode*)malloc(sizeof(QueueNode));
newNode->data = 10;
newNode->next = NULL;

    此时 newNode 的内存结构：

    newNode: { data = 10, next -> NULL }

  2. 检查队列是否为空：

    if (Q->rear == NULL) { // 队列为空Q->front = Q->rear = newNode; // front 和 rear 都指向新节点
}

    插入后的队列：

    Q: { front -> [10|next->NULL], rear -> [10|next->NULL] }

    可视化：

    Q->front↓
[10|NULL]↑
Q->rear

3. 插入第二个元素（Enqueue）
再插入 20：

Enqueue(Q, 20);

步骤分析：

  1. 创建新节点：

    QueueNode *newNode = (QueueNode*)malloc(sizeof(QueueNode));
newNode->data = 20;
newNode->next = NULL;

    newNode 的内存结构：

    newNode: { data = 20, next -> NULL }

  2. 队列不为空，直接插入队尾：

    else {Q->rear->next = newNode; // 当前队尾的 next 指向新节点Q->rear = newNode;       // rear 指针移动到新节点
}

    关键赋值过程：

    • Q->rear->next = newNode：
      让原来的队尾节点（10）的 next 指向 newNode（20）。
    • Q->rear = newNode：
      更新 rear 指针，使其指向新的队尾（20）。

    插入后的队列：

    Q: { front -> [10|next->20] -> [20|next->NULL], rear -> [20|next->NULL] }

    可视化：

    Q->front↓
[10|next] -> [20|NULL]↑Q->rear

4. 插入第三个元素（Enqueue）
再插入 30：

Enqueue(Q, 30);

步骤分析：

  1. 创建新节点：

    QueueNode *newNode = (QueueNode*)malloc(sizeof(QueueNode));
newNode->data = 30;
newNode->next = NULL;

    newNode 的内存结构：

    newNode: { data = 30, next -> NULL }

  2. 队列不为空，插入队尾：

    Q->rear->next = newNode; // 当前队尾（20）的 next 指向 30
Q->rear = newNode;       // rear 指针移动到 30

    插入后的队列：

    Q: { front -> [10|next->20] -> [20|next->30] -> [30|next->NULL], rear -> [30|next->NULL] }

    可视化：

    Q->front↓
[10|next] -> [20|next] -> [30|NULL]↑Q->rear

5. 总结 Q->front 和数据的赋值关系

操作Q->front 指向Q->rear 指向队列结构
初始NULLNULL空队列
插入 10[10|NULL][10|NULL]front → 10 ← rear
插入 20[10|next→20][20|NULL]front → 10 → 20 ← rear
插入 30[10|next→20][30|NULL]front → 10 → 20 → 30 ← rear

关键点：

  1. Q->front 永远指向队列的第一个元素（队头），Q->rear 永远指向队列的最后一个元素（队尾）。
  2. 插入元素时：
    • 如果队列为空，front 和 rear 都指向新节点。
    • 如果队列不为空：
      • Q->rear->next = newNode：让当前队尾的 next 指向新节点。
      • Q->rear = newNode：更新 rear 指针，使其指向新节点。
  3. Q->front 仅在队列为空时被修改，否则它一直指向第一个节点。

6. 代码示例（完整 Enqueue 函数）

void Enqueue(LinkedQueue *Q, int value) {QueueNode *newNode = (QueueNode*)malloc(sizeof(QueueNode));newNode->data = value;newNode->next = NULL;if (Q->rear == NULL) { // 队列为空Q->front = Q->rear = newNode;} else { // 队列不为空Q->rear->next = newNode; // 当前队尾的 next 指向新节点Q->rear = newNode;       // rear 指针移动到新节点}
}

这样，每次插入新元素时，Q->front 和 Q->rear 都会正确维护队列的头部和尾部，确保队列的 FIFO（先进先出） 特性。

三、栈与队列的相互实现（简要介绍）

3.1 用栈实现队列

使用两个栈可以实现一个队列的功能，基本思路是：

  1. 一个栈(instack)专门用于入队操作
  2. 另一个栈(outstack)专门用于出队操作
  3. 当outstack为空时，将instack的所有元素弹出并压入outstack

这样，元素的顺序就被反转了两次(先进后出→先进先出→先进后出)，最终实现了先进先出的队列特性。

typedef struct {Stack instack;  // 入队栈Stack outstack; // 出队栈
} MyQueue;// 初始化队列
void MyQueueInit(MyQueue *Q) {InitStack(&Q->instack);InitStack(&Q->outstack);
}// 入队
void MyQueuePush(MyQueue *Q, int value) {Push(&Q->instack, value);
}// 出队
int MyQueuePop(MyQueue *Q) {if (IsEmpty(&Q->outstack)) {// 将instack的所有元素转移到outstackwhile (!IsEmpty(&Q->instack)) {Push(&Q->outstack, Pop(&Q->instack));}}return Pop(&Q->outstack);
}// 查看队头
int MyQueuePeek(MyQueue *Q) {if (IsEmpty(&Q->outstack)) {// 将instack的所有元素转移到outstackwhile (!IsEmpty(&Q->instack)) {Push(&Q->outstack, Pop(&Q->instack));}}return Peek(&Q->outstack);
}// 判断队列是否为空
bool MyQueueEmpty(MyQueue *Q) {return IsEmpty(&Q->instack) && IsEmpty(&Q->outstack);
}

3.2 用队列实现栈

使用两个队列可以实现一个栈的功能，基本思路是：

  1. 一个队列(q1)作为主队列，另一个队列(q2)作为辅助队列
  2. 入栈操作直接入队到非空队列(若都为空则任选一个)
  3. 出栈操作时，将非空队列的前n-1个元素出队并入队到另一个队列，然后出队最后一个元素。
typedef struct {Queue q1;Queue q2;
} MyStack;// 初始化栈
void MyStackInit(MyStack *S) {InitQueue(&S->q1);InitQueue(&S->q2);
}// 入栈
void MyStackPush(MyStack *S, int value) {if (!IsEmpty(&S->q1)) {Enqueue(&S->q1, value);} else {Enqueue(&S->q2, value);}
}// 出栈
int MyStackPop(MyStack *S) {Queue *nonEmpty = IsEmpty(&S->q1) ? &S->q2 : &S->q1;Queue *empty = IsEmpty(&S->q1) ? &S->q1 : &S->q2;// 将非空队列的前n-1个元素转移到空队列while (Size(nonEmpty) > 1) {Enqueue(empty, Dequeue(nonEmpty));}return Dequeue(nonEmpty);
}// 查看栈顶
int MyStackTop(MyStack *S) {Queue *nonEmpty = IsEmpty(&S->q1) ? &S->q2 : &S->q1;Queue *empty = IsEmpty(&S->q1) ? &S->q1 : &S->q2;int value;// 将非空队列的所有元素转移到空队列，记录最后一个元素while (!IsEmpty(nonEmpty)) {value = Dequeue(nonEmpty);Enqueue(empty, value);}return value;
}// 判断栈是否为空
bool MyStackEmpty(MyStack *S) {return IsEmpty(&S->q1) && IsEmpty(&S->q2);
}

四、栈与队列的应用场景

4.1 栈的应用

  1. 函数调用栈：程序执行时，函数调用和返回的地址、参数、局部变量等都存储在调用栈中。

  2. 表达式求值：计算机使用栈来计算中缀表达式的值，需要创建算符栈(OPTR)和操作数栈(OPND)。处理规则包括：

    • 扫描到数，压入OPND栈
    • 扫描到运算符，与OPTR栈顶运算符比较优先级
    • 若优先级高则入栈，低则从OPND弹出两个数计算并将结果压回OPND

  3. 括号匹配：编译器检查代码中的括号是否匹配，使用栈来存储遇到的左括号，遇到右括号时弹出栈顶元素检查是否匹配。

  4. 浏览器前进后退：浏览器使用两个栈分别存储已访问和已后退的页面，实现前进后退功能。

  5. 深度优先搜索(DFS)：图的DFS算法使用栈来存储待访问的节点。

4.2 队列的应用

  1. 任务调度：操作系统使用队列管理等待执行的进程，如打印任务队列。

  2. 广度优先搜索(BFS)：图的BFS算法使用队列来存储待访问的节点。

  3. 消息队列：分布式系统中，不同服务之间通过消息队列进行异步通信。

  4. 缓冲区：数据流处理中，队列作为缓冲区平衡生产者和消费者的速度差异。

  5. CPU调度：操作系统使用多种队列算法(如轮转调度)管理CPU时间片的分配。

五、栈与队列的扩展知识

5.1 共享栈

共享栈是一种利用同一数组空间实现两个栈的结构，一个栈的栈底在数组起始位置，另一个栈的栈底在数组末尾，两个栈向中间增长，可以更有效地利用存储空间。

#define MAX_SIZE 100typedef struct {int data[MAX_SIZE];int top1; // 栈1的栈顶指针int top2; // 栈2的栈顶指针
} SharedStack;// 初始化共享栈
void InitSharedStack(SharedStack *S) {S->top1 = -1;S->top2 = MAX_SIZE;
}// 栈1入栈
void Push1(SharedStack *S, int value) {if (S->top1 + 1 == S->top2) {printf("栈满\n");return;}S->data[++S->top1] = value;
}// 栈2入栈
void Push2(SharedStack *S, int value) {if (S->top2 - 1 == S->top1) {printf("栈满\n");return;}S->data[--S->top2] = value;
}

5.2 双端队列(Deque)

双端队列是一种允许在两端进行插入和删除操作的线性表，可以看作是栈和队列的结合体。双端队列的实现通常基于双向链表或循环数组。

5.3 优先队列(Priority Queue)

优先队列中的每个元素都有优先级，出队操作总是移除优先级最高的元素。优先队列通常使用堆(Heap)数据结构实现。

六、总结

栈和队列作为基础数据结构，在计算机科学中有着广泛的应用。理解它们的特性和实现原理，对于编写高效、可靠的程序至关重要。通过本文的学习，你应该已经掌握了：

  1. 栈和队列的基本概念及操作
  2. 顺序和链式两种存储结构的实现方式
  3. 如何用栈实现队列和用队列实现栈
  4. 栈和队列在实际开发中的典型应用场景
  5. 一些高级变体如共享栈、双端队列等

在实际编程中，大多数语言的标准库已经提供了栈和队列的实现(如C++的stack和queue)，但在理解底层原理的基础上，我们能够更好地选择和使用这些数据结构，甚至根据特定需求进行定制化扩展。

希望本文能帮助你深入理解栈和队列这两种基础但强大的数据结构，并在未来的编程实践中灵活运用它们。

参考文献：数据结构：栈和队列(Stack & Queue)【详解】

http://www.lryc.cn/news/616093.html

相关文章：

  • 从0开始的中后台管理系统-5（userList页面功能实现）
  • JS数组排序算法
  • 第三章 向量
  • ECharts Y轴5等分终极解决方案 - 动态适配缩放场景
  • 计算机网络：（十四）传输层（下）详细讲解TCP报文段的首部格式，TCP 可靠传输的实现与TCP 的流量控制
  • 一些js数组去重的实现算法
  • Android的事件分发流程、Kotlin协程、4大组件、Handler机制、架构设计、性能优化、内存泄漏
  • 系统架构设计师备考之架构设计高级知识
  • Flink提交流程全解析：从模式到实践
  • DevOps：从GitLab .gitlab-ci.yml 配置文件到CI/CD
  • [论文阅读] 人工智能 + 软件工程 | 大型语言模型对决传统方法：多语言漏洞修复能力大比拼
  • FlinkSQL Joins全解析
  • 从MySQL到大数据平台：基于Spark的离线分析实战指南
  • Spark学习（Pyspark）
  • 在VMware中安装统信UOS桌面专业版
  • 可视化程序设计(4) - 第一个图形窗口程序
  • Python元组
  • 计算XGBoost分类模型的错误率
  • Qt 框架全面解析：从基础到应用
  • 基于C语言（兼容C++17编译器）的记账系统实现
  • CompletableFuture实现Excel sheet页导出
  • RabbitMQ面试精讲 Day 19：网络调优与连接池管理
  • GitHub上为什么采用Gradle编译要多于Maven
  • Excel合并同步工具V1.0
  • Pytorch深度学习框架实战教程10：Pytorch模型保存详解和指南
  • Spring Boot集成WebSocket
  • Spring Boot与WebSocket构建物联网实时通信系统
  • Android Intent 解析
  • Leetcode 3644. Maximum K to Sort a Permutation
  • 数学建模——回归分析