数学建模：控制预测类问题

前言

梅姨阁诗人……

一、回归分析模型

1.基本概念

回归分析就是在寻找存在一定关系的变量间的数学表达式，通常被用来进行预测和推断。根据变量的数目可以分为一元回归和多元回归，根据自变量与因变量的表现形式可以分为线性回归和非线性回归。

对于每个自变量，其对应在表达式上的值称为估计值，而其实际对应的值称为观测值。残差就是观测值减去估计值。

2.一元线性回归

（1）模型

一元线性回归模型可以表示为。其中表示截距，表示斜率，表示误差项，即反应除了x和y之间线性关系之外的因素对y的影响。这里，y表示的是观测值。而如果要求y的期望值，那么对应的回归方程就是。

（2）回归方程的求解——最小二乘法

最小二乘法就是求解一元线性回归方程。

首先，最小二乘法需要求出x的平均值和y的平均值，回归直线必然通过这个点。

之后，需要计算三个关键量，即x，y的离差平方和以及xy乘积的离差乘积和。公式就是

Sxx和Syy的含义就是该变量间的差异大小，数值越大，表示每个变量间的差异越大。而Sxy表示x和y两变量间的关系程度。Sxy大于0表示正相关，小于0表示负相关，绝对值越大表示两者的相关性越大。

之后计算两个回归系数和。公式就是

此时我们就得到了这个一元线性回归方程。根据这个方程，我们就可以求得y的预测值。而用实际值减去预测值，就可以得到残差e。

（3）回归模型的检验

首先，回归直线与各观测点的接近程度称为回归直线对数据的拟合优度。其中包括三个指标，分别为总平方和（TSS），回归平方和（ESS）和残差平方和（RSS）。

这里，总平方和TSS的含义是总变异，回归平方和ESS表示能用该模型解释的变异，残差平方和RSS表示不能用该模型解释的变异，所以就有TSS等于ESS加上RSS。

再引入决定系数：

其中，的数值n的意义是该自变量因素x可以解决百分之n的问题，剩下的部分可能是由其他因素造成的。这里，位于0到1之间，越大表示拟合程度越好。

（4）显著性检验

因为在最初求回归方程时，是先假定x和y之间存在线性关系，且误差符合正态分布，然后再求得回归方程，所以这个假设成不成立还需要进行检验。所以，对应两个假设，显著性检验包括线性关系检验和回归系数检验。

首先，先计算均方误差MSE：

MSE的含义是残差平方和的平均值，其数值越小表示该模型的预测越完美。

之后计算斜率标准误：

斜率标准误的含义就是计算出的这个斜率在真实斜率周围的分散程度，即如果重复收集数据，这个计算出的估计斜率会变化多少。

线性关系检验就是计算F检验：

回归系数检验就是计算t检验：

在一元线性回归中F检验和t检验等价：

因为当你说t检验显著，即说明当前这个回归系数显著，那么肯定就能表明线性关系显著，因而一般直接进行t检验即可。

之后就是计算t检验的p值。t检验的p值的含义就是，假设当前情境下的自变量和因变量无关的前提下，产生当前数据或更贴合的数据的概率。计算出p值后，一般取0.05和p值比较，如果小于，则说明上述假设不成立，即可以说明当前自变量和因变量存在显著线性关系。

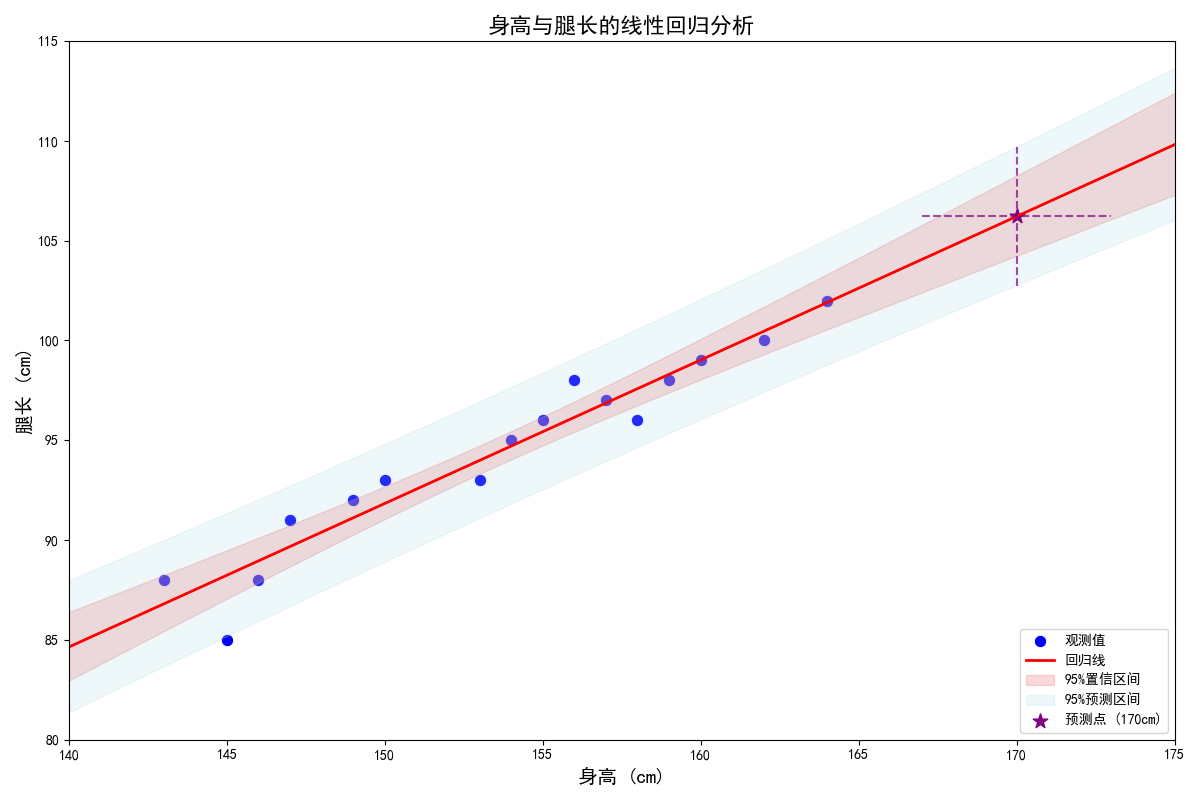
（5）计算置信区间和预测区间

通过要求的自变量x和回归方程，在计算出因变量的预测值y后，就可以计算该自变量x对的应的的置信区间和预测区间。

首先，置信区间的含义是，所有自变量为x的样本的预测值y的平均值会落在这个区间里。举个例子，倘若我现在有了cf每天的训练时长和rating的回归方程，那么对于自变量训练时长2h，置信区间就是所有训练时长为2h的人的rating的平均值的范围。

之后，预测区间的含义是，单个自变量为x的样本的预测值y的范围。同样例子里，那就是训练时长为2h的某一个人的rating范围。所以，根据含义可以得到，预测区间一般会比置信区间大一点，因为单个情况肯定会有个体差异，比如天赋或者训练效率。

其中，置信区间的公式为

预测区间的公式为：

其中，x为要计算预测值的自变量。的含义是有的概率落在这个区间里，一般是通过查表得到的，又因为一般取0.05，所以该值就是3.182。

（6）例题

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#统计数据可视化库
import seaborn as sns
#统计计算库
from scipy import stats#使用中文字体
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False#输入数据
height = np.array([143, 145, 146, 147, 149, 150, 153, 154, 155, 156, 157, 158, 159, 160, 162, 164])
leg_length = np.array([88, 85, 88, 91, 92, 93, 93, 95, 96, 98, 97, 96, 98, 99, 100, 102])#创建DataFrame
data = pd.DataFrame({'身高': height, '腿长': leg_length})
print("部分原始数据:")
print(data.head())#基本统计量计算n = len(height)  #样本量
x_mean = np.mean(height)  #身高平均值
y_mean = np.mean(leg_length)  #腿长平均值#计算三个关键离差平方和
sxx = np.sum((height - x_mean)**2)  #身高离差平方和
syy = np.sum((leg_length - y_mean)**2)  #腿长离差平方和
sxy = np.sum((height - x_mean) * (leg_length - y_mean))  #离差乘积和print("\n基本统计量:")
print(f"样本量 n = {n}")
print(f"身高均值 = {x_mean:.2f} cm, 腿长均值 = {y_mean:.2f} cm")
print(f"Sxx = {sxx:.2f}")
print(f"Syy = {syy:.2f}")
print(f"Sxy = {sxy:.2f}")#回归系数计算beta_1 = sxy / sxx  #斜率
beta_0 = y_mean - beta_1 * x_mean  #截距print("\n回归系数:")
print(f"斜率 β₁ = {beta_1:.4f}")
print(f"截距 β₀ = {beta_0:.4f}")#回归方程
print(f"回归方程: y = {beta_0:.4f} + {beta_1:.4f}x")#模型拟合评估#计算预测值和残差
y_pred = beta_0 + beta_1 * height
e = leg_length - y_pred#计算平方和
ess = np.sum(e**2)  #残差平方和 (ESS)
tss = syy  #总平方和 (TSS)
rss = tss - ess  #回归平方和 (RSS)#计算拟合优度
r_squared = rss / tss  #决定系数
mse = ess / (n-2)  #均方误差print("\n模型拟合评估:")
print(f"残差平方和 (ESS) = {ess:.2f}")
print(f"回归平方和 (RSS) = {rss:.2f}")
print(f"总平方和 (TSS) = {tss:.2f}")
print(f"决定系数 R² = {r_squared:.4f}")
print(f"均方误差 (MSE) = {mse:.4f}")#显著性检验#斜率标准误
se_beta1 = np.sqrt(mse / sxx)#t检验统计量
t_stat_beta1 = beta_1 / se_beta1#p值计算 (双侧检验)
t_p_value_beta1 = 2 * (1 - stats.t.cdf(np.abs(t_stat_beta1), n-2))print("\n显著性检验:")
print(f"斜率标准误 = {se_beta1:.4f}")
print(f"斜率t统计量 = {t_stat_beta1:.4f}, p值 = {t_p_value_beta1:.6f}")#置信区间与预测区间#预测身高170cm的腿长
predict_height = 170
predicted_leg = beta_0 + beta_1 * predict_height#置信区间函数
def confidence_interval(x, alpha=0.05):t_val = stats.t.ppf(1 - alpha/2, df=n-2)se_fit = np.sqrt(mse * (1/n + (x - x_mean)**2 / sxx))margin = t_val * se_fitlower = (beta_0 + beta_1 * x) - marginupper = (beta_0 + beta_1 * x) + marginreturn lower, upper#预测区间函数
def prediction_interval(x, alpha=0.05):t_val = stats.t.ppf(1 - alpha/2, df=n-2)se_pred = np.sqrt(mse * (1 + 1/n + (x - x_mean)**2 / sxx))margin = t_val * se_predlower = (beta_0 + beta_1 * x) - marginupper = (beta_0 + beta_1 * x) + marginreturn lower, upper#计算区间
ci_lower, ci_upper = confidence_interval(predict_height)
pi_lower, pi_upper = prediction_interval(predict_height)print("\n预测结果 (身高170cm):")
print(f"点预测腿长 = {predicted_leg:.2f} cm")
print(f"95%置信区间 = [{ci_lower:.2f}, {ci_upper:.2f}] cm (平均腿长范围)")
print(f"95%预测区间 = [{pi_lower:.2f}, {pi_upper:.2f}] cm (个体腿长范围)")#可视化#创建画布
plt.figure(figsize=(12, 8))#回归线及置信和预测区间#绘制原始数据点
sns.scatterplot(x='身高', y='腿长', data=data, s=80, color='blue', label='观测值')#生成回归线
x_values = np.linspace(min(height)-5, max(height)+15, 100)
y_reg = beta_0 + beta_1 * x_values
plt.plot(x_values, y_reg, color='red', linewidth=2, label='回归线')#计算并绘制置信区间
ci_lower_all = [confidence_interval(x)[0] for x in x_values]#将直线上的散点传入计算对应的上下界
ci_upper_all = [confidence_interval(x)[1] for x in x_values]
plt.fill_between(x_values, ci_lower_all, ci_upper_all, color='lightcoral', alpha=0.3, label='95%置信区间')#计算并绘制预测区间
pi_lower_all = [prediction_interval(x)[0] for x in x_values]
pi_upper_all = [prediction_interval(x)[1] for x in x_values]
plt.fill_between(x_values, pi_lower_all, pi_upper_all, color='lightblue', alpha=0.2, label='95%预测区间')#绘制预测点
plt.scatter(predict_height, predicted_leg, s=120, color='purple', marker='*', label=f'预测点 (170cm)')
plt.vlines(predict_height, pi_lower, pi_upper, color='purple', linestyle='--', alpha=0.7)
plt.hlines(predicted_leg, predict_height-3, predict_height+3, color='purple', linestyle='--', alpha=0.7)#添加标题和标签
plt.title('身高与腿长的线性回归分析', fontsize=16)
plt.xlabel('身高 (cm)', fontsize=14)
plt.ylabel('腿长 (cm)', fontsize=14)
plt.legend(loc='lower right', fontsize=10)plt.xlim(140, 175)
plt.ylim(80, 115)plt.tight_layout()
plt.show()

这里的p值计算直接就用的库里的函数。

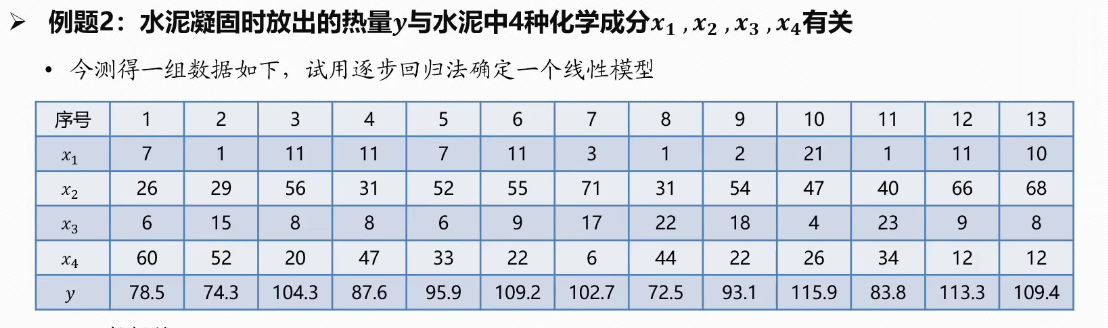
3.多元线性回归分析

形如的回归模型称为k元线性回归模型，也可以写成矩阵形式，其中为误差。

求解方法就是用最小二乘法求解自变量x的系数，估计值的求解公式为，然后把求得的系数代入方程即可。

之后跟一元线性回归类似，还是要先计算TSS，RSS和ESS，再计算决定系数。

要注意的是，在多元线性回归模型中需要引入调整，因为常规的会因为自变量的增加而增加，这体现在实际中就是过拟合，即引入了大量无用的变量来增加模型的拟合程度。而调整通过增加来除以变量数，从而将常规的这个弊端消除了。

然后，在求解实际问题中，其实并不确定有哪些自变量是真正影响因变量的因素。所以一般会对这些自变量进行逐步回归法，进而找出应该包含在最终模型里的自变量。而逐步回归法就是每次计算单个自变量t检验的偏p值，每次选择最小的且小于显著性水平的自变量加入，每次加入后计算所有当前在模型里的自变量的整体p值，然后剔除大于显著性水平的自变量，之后重复直到模型的自变量不再变化。

import numpy as np
import pandas as pd
#回归分析库
import statsmodels.api as sm
#用于标准化
from sklearn.preprocessing import StandardScaler#初始数据
data = {'x1': [7, 1, 11, 11, 7, 11, 3, 1, 2, 21, 1, 11, 10],'x2': [26, 29, 56, 31, 52, 55, 71, 31, 54, 47, 40, 66, 68],'x3': [6, 15, 8, 8, 6, 9, 17, 22, 18, 4, 23, 9, 8],'x4': [60, 52, 20, 47, 33, 22, 6, 44, 22, 26, 34, 12, 12],'y': [78.5, 74.3, 104.3, 87.6, 95.9, 109.2, 102.7, 72.5, 93.1, 115.9, 83.8, 113.3, 109.4]
}
df = pd.DataFrame(data)#定义逐步回归函数
def stepwise_selection(X, y,initial_list=[],#初始变量列表threshold_in=0.05,#进入模型的p值阈值threshold_out=0.10,#移除模型的p值阈值verbose=True):#打印步骤信息#加入的变量列表included = list(initial_list)while True:changed = False#前向选择#抓出当前未包含在模型内的变量的列表excluded = list(set(X.columns) - set(included))#存储候选变量的p值new_pval = pd.Series(index=excluded, dtype=float)#遍历每个候选变量for new_column in excluded:#构建包含当前候选变量的临时模型model = sm.OLS(y, sm.add_constant(pd.DataFrame(X[included + [new_column]]))).fit()#计算p值new_pval[new_column] = model.pvalues[new_column]#取出最小值best_pval = new_pval.min()#若最小值小于阈值if best_pval < threshold_in:#获取对应的变量名best_feature = new_pval.idxmin()#加入变量列表included.append(best_feature)changed = True#打印if verbose:print(f'添加变量 {best_feature} (p值 = {best_pval:.6f})')#后向剔除#复制一个临时模型model = sm.OLS(y, sm.add_constant(pd.DataFrame(X[included]))).fit()#提取p值pvalues = model.pvalues.iloc[1:]#p值最大值worst_pval = pvalues.max()#大于阈值if worst_pval > threshold_out:changed = True#提取标签worst_feature = pvalues.idxmax()#移除included.remove(worst_feature)#打印if verbose:print(f'移除变量 {worst_feature} (p值 = {worst_pval:.6f})')#不发生改变了就停止if not changed:breakreturn included#准备数据
X = df[['x1', 'x2', 'x3', 'x4']]
y = df['y']#执行逐步回归
print("逐步回归过程:")
selected_features = stepwise_selection(X, y, verbose=True)#使用选定的变量拟合最终模型
X_final = sm.add_constant(X[selected_features])
model = sm.OLS(y, X_final).fit()#打印最终模型结果
print("最终回归模型结果:")
print(model.summary())#打印模型方程
print("\n最终模型方程:")
print(f"y = {model.params['const']:.4f}", end="")for feature in selected_features:coef = model.params[feature]print(f" + {coef:.4f}*{feature}", end="")#打印模型评估指标
print("\n模型评估指标:")
print(f"R² = {model.rsquared:.4f}")
print(f"调整 R² = {model.rsquared_adj:.4f}")
print(f"F统计量 = {model.fvalue:.2f}")
print(f"F检验 p值 = {model.f_pvalue:.6e}")

逐步回归法就是一个条件为true的循环，每次看能否新增或者移除，用一个bool变量记录是否改变过，如果没改变过就直接break。

4.非线性回归

一般情况下，很多关系都不是简单线性关系，其图像会是一个曲线，此时就需要用非线性回归进行拟合了。非线性回归首先就需要确定方程的类型，一般就是先画出散点图，再通过观察确定用哪种方程去拟合。一般情况下可以选择二次函数（幂函数），对数函数，指数函数和反比例函数，当然具体的还需要查一些资料来找更合适的函数去拟合。

当无法确定用什么方程时，可以选择使用多项式回归来求解。

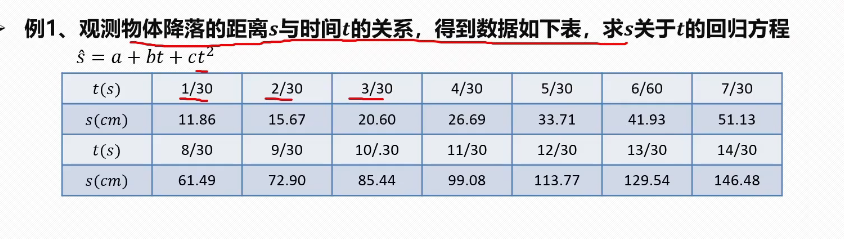
观察数据点的分布可以考虑使用二次函数拟合，然后求这三个参数即可。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from scipy.optimize import curve_fit
import statsmodels.api as sm
#使用中文字体
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False#数据准备
t_values = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]) / 30  # 转换为秒
s_values = np.array([11.86, 15.67, 20.60, 26.69, 33.71, 41.93, 51.13, 61.49,72.90, 85.44, 99.08, 113.77, 129.54, 146.48])#转化为线性回归问题print("="*50)
print("方法1：多项式回归（线性回归方法）")
print("="*50)#转换为列向量
X_poly = t_values.reshape(-1, 1)
#创建多项式特征 (t, t^2)，不包含常数项
poly = PolynomialFeatures(degree=2, include_bias=False)
#拟合并转换
X_poly_trans = poly.fit_transform(X_poly)#添加常数项
X_poly_trans = sm.add_constant(X_poly_trans)#拟合线性模型
model_poly = sm.OLS(s_values, X_poly_trans).fit()#获取系数
a, b, c = model_poly.params
print(f"回归方程: s = {a:.4f} + {b:.4f}t + {c:.4f}t²")
print(f"系数: a = {a:.4f}, b = {b:.4f}, c = {c:.4f}")#模型评估
print("\n模型评估:")
print(f"R² = {model_poly.rsquared:.6f}")
print(f"调整R² = {model_poly.rsquared_adj:.6f}")
print(f"残差平方和 (RSS) = {model_poly.ssr:.4f}")#预测值
s_pred_poly = model_poly.predict(X_poly_trans)#结果
print("\n" + "="*50)
print("结果展示")
print("="*50)
print(f"多项式回归系数: a={a:.4f}, b={b:.4f}, c={c:.4f}")#定义二次函数模型
def quadratic_model(t, a, b, c):return a + b*t + c*t**2#创建更密集的时间点用于平滑曲线绘制
t_smooth = np.linspace(t_values.min(), t_values.max(), 100)#可视化结果
plt.figure(figsize=(12, 8))#原始数据
plt.scatter(t_values, s_values, color='blue', s=80, label='原始数据', zorder=5)#多项式回归拟合曲线，直接拟合二次函数
plt.plot(t_smooth, quadratic_model(t_smooth, a, b, c),'r-', linewidth=2.5, label='多项式回归拟合', alpha=0.8)#添加图例和标签
plt.title('物体下落距离与时间关系', fontsize=16, fontweight='bold')
plt.xlabel('时间 (s)', fontsize=14)
plt.ylabel('距离 (cm)', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)#添加回归方程文本
eq_text_poly = f"多项式回归: $s = {a:.2f} + {b:.2f}t + {c:.2f}t^2$"
plt.text(0.05, 0.95, eq_text_poly, transform=plt.gca().transAxes,fontsize=12, verticalalignment='top', bbox=dict(facecolor='white', alpha=0.8))#添加R²值
r2_text = f"$R^2 = {model_poly.rsquared:.6f}$"
plt.text(0.05, 0.80, r2_text, transform=plt.gca().transAxes,fontsize=12, verticalalignment='top', bbox=dict(facecolor='white', alpha=0.8))plt.tight_layout()
plt.show()

这里用的方法是，讲二次项当作另一个变量，将非线性问题转化成多元线性问题，然后直接求参数即可。

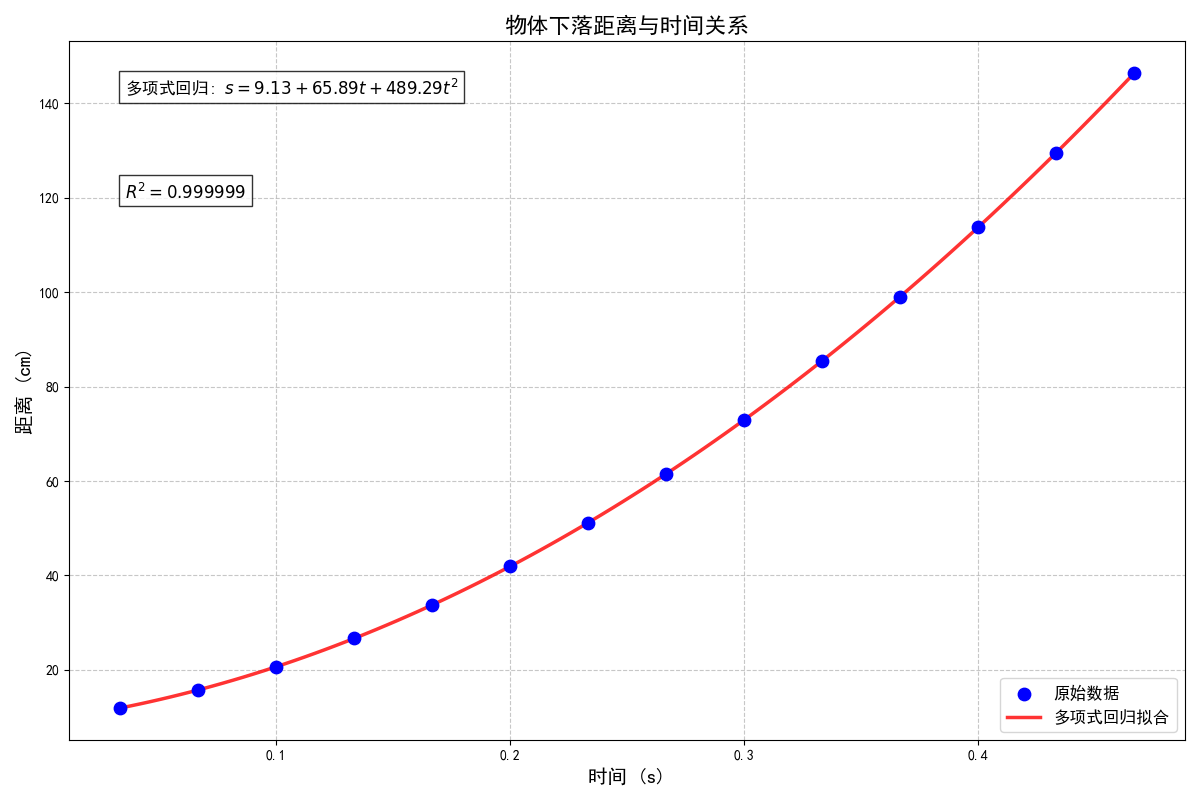
要是比赛也都是这种数据该多好……

5.逻辑回归

（1）基本概念

逻辑回归和前面的回归模型不同，它解决的其实是二分问题。举个例子，假如我要预测方舟下一个出的角色是男是女，因为一共就只有两种可能，所以要预测的这个性别就是离散的变量，逻辑回归就是用来预测离散变量属于哪一类的。

逻辑回归的函数为sigmoid函数，这个函数的值域就是[0,1]，表示输入变量x属于类别1的概率。那么我们就可以根据其输出的值来判断更有可能属于哪个类别，以下是sigmoid函数的图像：

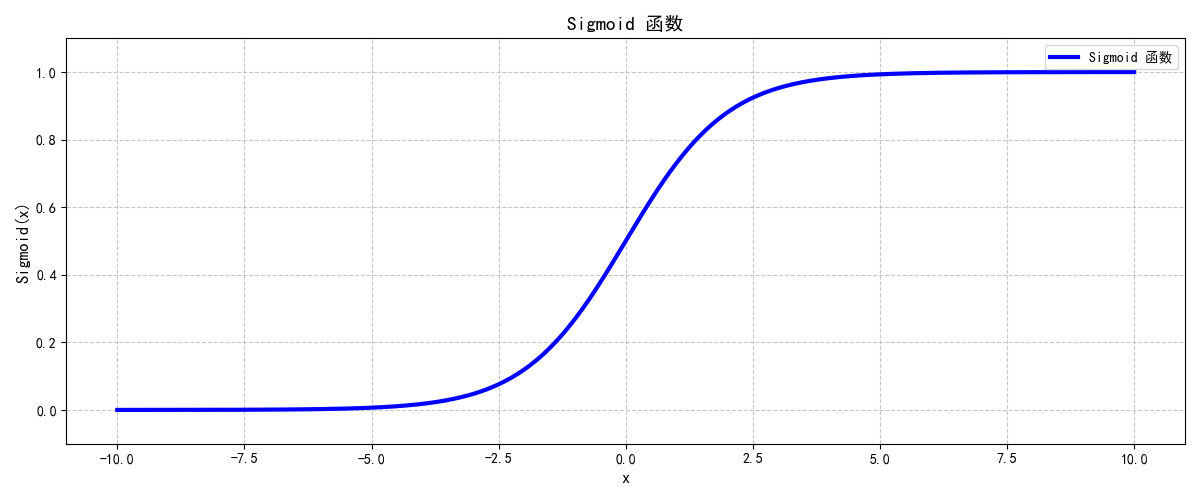
一般来说，要预测的类型肯定不会只有一个参数，所以要先训练得到各个参数的权值，得到所有参数的加权后的线性模型，然后把这个模型的函数值z作为自变量传入Sigmoid函数，公式为：

（2）极大似然估计

极大似然估计就是给定模型后，通过收集数据，求该模型的参数。

举个例子，假如现在抛十次硬币，六次正面，四次反面。似然函数的含义是，对于不同的概率，使得我们观测到六次正面四次反面的概率有多大。假如用表示该硬币为正面的概率，那么似然函数就是：

更白话一点，似然函数就是在给定的数据的情况下，参数取某个特定值的合理程度。注意，似然函数不是在估计概率，而是在衡量不同的参数值对当前已有数据的解释能力。假如为正面的概率为，那么似然函数的值表示我们在这个概率下观测到六正四反的概率。

所以，最大似然估计就是最大化这个似然函数，即求这个函数的极大值点。那么很好理解，就是找使得当前数据最合理的参数，那么就可以把这个值作为估计值。

（3）损失函数与梯度下降

这俩太复杂了，既然python里都有封装好的函数，这里就只提一下吧……

损失函数就是衡量该模型准确率的函数，那么需要做的就是最小化这个损失。而梯度下降法就是选择损失函数下降最快的方向，使得模型快速调整到最准确的状态。其实除此之外还有别的算法，python里根据数据情况选一个即可，计算机就自己运行了。

（4）鸢尾花数据集预测品种

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
#将数据集分为训练集和测试集
from sklearn.model_selection import train_test_split
#计算准确度、展示分类结果、生成报告
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
#处理缺失值
from sklearn.impute import SimpleImputer
import seaborn as sns
#使用中文字体
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False#数据加载与预处理
df = pd.read_excel('iris_dataset.xlsx', sheet_name='Sheet1')#只取前100个样本（Setosa和Versicolor）
df = df.head(100)#处理缺失值
print("缺失值统计:")
print(df.isnull().sum())#填充缺失值 -> 使用特征列的平均值
imputer = SimpleImputer(strategy='mean')
features = ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
df[features] = imputer.fit_transform(df[features])#移除标签缺失的样本
df = df.dropna(subset=['species'])#创建二分类标签 (Setosa=0, Versicolor=1)
df['target'] = df['species'].map({'setosa': 0, 'versicolor': 1})#准备训练数据
X = df[features]
y = df['target']#划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42
)print(f"训练集大小: {X_train.shape[0]}")
print(f"测试集大小: {X_test.shape[0]}")#训练逻辑回归模型
model = LogisticRegression(penalty='l2',  #L2正则化防止过拟合C=1.0,  #正则化强度solver='lbfgs',  #优化算法max_iter=200,  #最大迭代次数random_state=42 #随机种子
)model.fit(X_train, y_train)#模型评估
#训练集预测
train_pred = model.predict(X_train)
train_acc = accuracy_score(y_train, train_pred)
print(f"训练集准确率: {train_acc:.4f}")#测试集预测
test_pred = model.predict(X_test)
test_acc = accuracy_score(y_test, test_pred)
print(f"测试集准确率: {test_acc:.4f}")#混淆矩阵
cm = confusion_matrix(y_test, test_pred)
plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues',xticklabels=['Setosa', 'Versicolor'],yticklabels=['Setosa', 'Versicolor'])
plt.xlabel('预测标签')
plt.ylabel('真实标签')
plt.title('混淆矩阵')
plt.show()#分类报告
print("\n分类报告:")
print(classification_report(y_test, test_pred, target_names=['Setosa', 'Versicolor']))#预测示例
print("\n预测示例:")
sample = pd.DataFrame({'sepal length (cm)': [5.1, 6.0, 5.5],'sepal width (cm)': [3.5, 2.7, 2.5],'petal length (cm)': [1.4, 4.5, 4.0],'petal width (cm)': [0.2, 1.5, 1.3]
})sample_pred = model.predict(sample)
sample_prob = model.predict_proba(sample)sample['预测品种'] = ['Setosa' if p == 0 else 'Versicolor' for p in sample_pred]
sample['Setosa概率'] = sample_prob[:, 0]
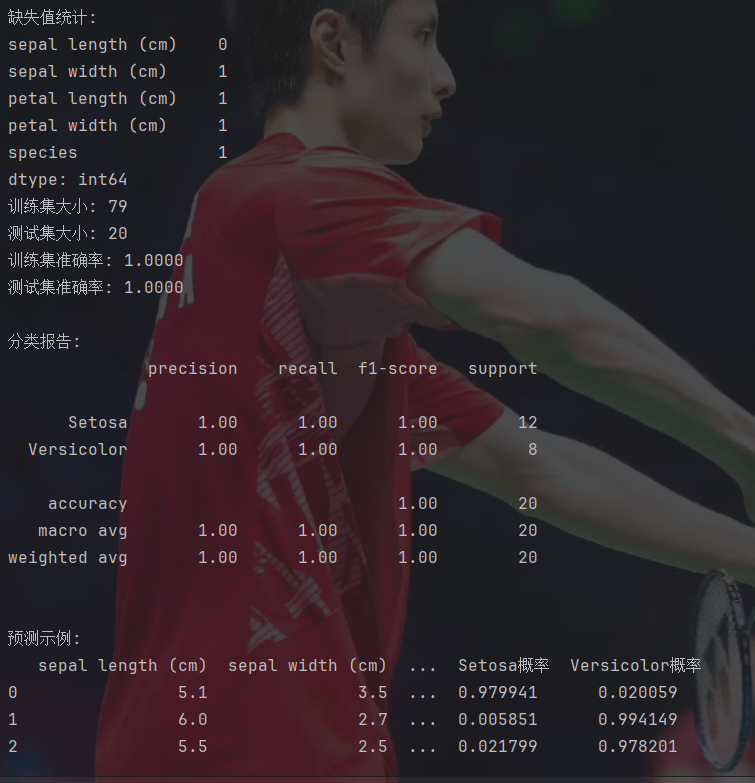
sample['Versicolor概率'] = sample_prob[:, 1]print(sample)

整体思路就是把所有数据以8：2的比例划分为训练集和测试集，先用训练集训练出模型，再用测试集测试模型的效果。

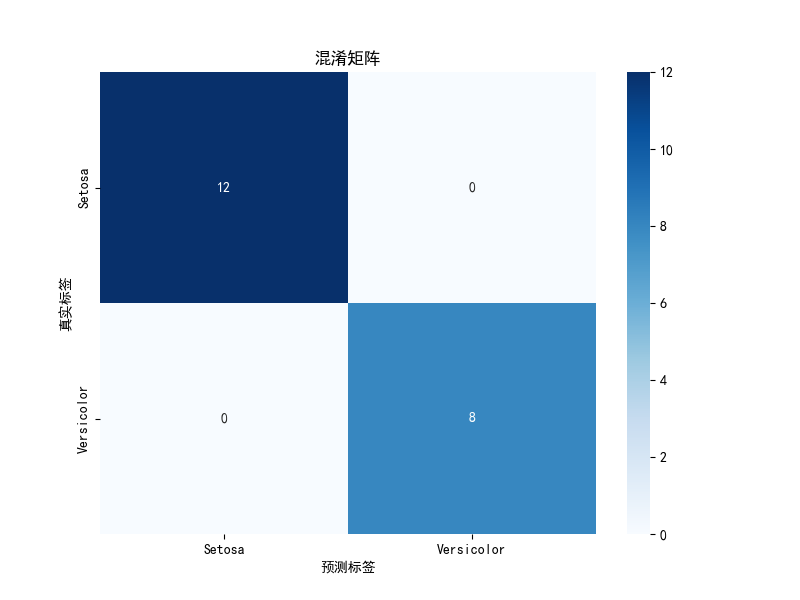
这张图里，纵坐标为真实标签，横坐标为预测的坐标。所以对角线格子的数量代表正确预测是数量，其余的格子为错误预测的数量。那么在这张图里，所有的预测都是正确的。

百分百预测率，无敌了。

二、灰色预测GM（1，1）

和灰色关联分析类似，灰色预测就是在信息量较少的情况下进行预测的模型，在这里，GM（1,1）的GM表示灰色模型grey model，而（1,1）表示的是含有一个变量的一阶微分方程。

求解GM（1,1）的步骤就是，首先求出原始序列的前缀和数列，削弱其随机性，然后根据这个前缀和数列建立一个微分方程模型，最后通过差分求得原始数据的估计值即可。

之后，在使用灰色预测模型之前，除了需要保证原始数据非负，还需要对原数据进行级比检验，可以进行灰色预测的数据应具有准指数级的规律。级比检验在GM（1,1）中就是判断每两个相邻的数据的比是否处于一个区间内，是的话就说明可以进行。一般情况下，只需要保证落在这个区间内的比例比较高即可。

在预测完后，一般还需要进行残差检验和级比偏差检验来判断这个模型的拟合效果是否良好。残差检验就是计算每个数据点的残差，一般如果绝对值都小于0.1说明效果很好，小于0.2说明效果一般。级比偏差检验就是根据公式计算平均级比偏差，然后同样判断是否小于0.1或0.2即可。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#使用中文字体
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False#原始数据
years = [1997, 1998, 1999, 2000, 2001, 2002]
months = ['1月', '2月', '3月', '4月', '5月', '6月', '7月', '8月', '9月', '10月', '11月', '12月']data = [[83.0, 79.8, 78.1, 85.1, 86.6, 88.2, 90.3, 86.7, 93.3, 92.5, 90.9, 96.9],[101.7, 85.1, 87.8, 91.6, 93.4, 94.5, 97.4, 99.5, 104.2, 102.3, 101.0, 123.5],[92.2, 114.0, 93.3, 101.0, 103.5, 105.2, 109.5, 109.2, 109.6, 111.2, 121.7, 131.3],[105.0, 125.7, 106.6, 116.0, 117.6, 118.0, 121.7, 118.7, 120.2, 127.8, 121.8, 121.9],[139.3, 129.5, 122.5, 124.5, 135.7, 130.8, 138.7, 133.7, 136.8, 138.9, 129.6, 133.7],[137.5, 135.3, 133.0, 133.4, 142.8, 141.6, 142.9, 147.3, 159.6, 162.1, 153.5, 155.9]
]#创建df
df = pd.DataFrame(data, index=years, columns=months)#级比检验函数
def ratio_test(series):#储存级比ratios = []n = len(series)#计算级比for i in range(1, n):ratio = series[i - 1] / series[i]ratios.append(ratio)#计算可容覆盖区间 -> 给定公式lower_bound = np.exp(-2 / (n + 1))upper_bound = np.exp(2 / (n + 1))#检查所有级比是否在可容覆盖区间内all_in_range = all(lower_bound <= ratio <= upper_bound for ratio in ratios)return ratios, (lower_bound, upper_bound), all_in_range#GM(1,1)模型函数
#predict_count: 预测点数
#返回拟合值, 预测值, 参数a,b, 相对残差, 级比偏差
def gm11(series, predict_count=1):n = len(series)#前缀和ago1 = np.cumsum(series)#紧邻均值生成序列z = np.array([(ago1[i - 1] + ago1[i]) / 2 for i in range(1, len(ago1))])#构造矩阵B和YB = np.column_stack((-z, np.ones(len(z))))Y = series[1:]#计算微分方程参数a, b# @ 为矩阵乘法运算符u = np.linalg.inv(B.T @ B) @ B.T @ Ya, b = u[0], u[1]#时间响应函数 -> 微分方程的解def time_response(k):return (series[0] - b / a) * np.exp(-a * k) + b / a#计算拟合值 -> 第一个点的拟合值等于原始值fitted_values = [series[0]]for k in range(1, n):ago1_fit = time_response(k)ago1_fit_prev = time_response(k - 1)#累减还原fitted_values.append(ago1_fit - ago1_fit_prev)#预测未来值predictions = []for k in range(n, n + predict_count):ago1_pred = time_response(k)ago1_pred_prev = time_response(k - 1)predictions.append(ago1_pred - ago1_pred_prev)#残差检验residuals = np.array(series) - np.array(fitted_values)#残差relative_errors = np.abs(residuals) / np.array(series)#相对残差#级比偏差检验#原始级比original_ratios = [series[i - 1] / series[i] for i in range(1, n)]#拟合级比fitted_ratios = [fitted_values[i - 1] / fitted_values[i] for i in range(1, n)]#级比偏差ratio_deviations = np.abs(np.array(original_ratios) - np.array(fitted_ratios))return fitted_values, predictions, a, b, relative_errors, ratio_deviations#对每个月分别进行预测和检验
monthly_predictions = {}
all_ratios = []
all_in_range = []
all_relative_errors = []
all_ratio_deviations = []
all_avg_relative_error = []
all_max_ratio_deviation = []plt.figure(figsize=(8, 20))
for i, month in enumerate(months):#提取该月的时间序列series = df[month].values#进行级比检验ratios, (lower_bound, upper_bound), in_range = ratio_test(series)all_ratios.append(ratios)all_in_range.append(in_range)#使用GM(1,1)进行预测和检验fitted_values, predictions, a, b, relative_errors, ratio_deviations = gm11(series)#存储结果monthly_predictions[month] = predictions[0]all_relative_errors.append(relative_errors)all_ratio_deviations.append(ratio_deviations)all_avg_relative_error.append(np.mean(relative_errors))all_max_ratio_deviation.append(np.max(ratio_deviations))#绘制拟合效果和预测plt.subplot(4, 3, i + 1)plt.plot(years, series, 'bo-', label='实际值', markersize=6)plt.plot(years, fitted_values, 'r--', label='拟合值')plt.plot(2003, predictions[0], 'g*', markersize=12, label='预测值')plt.title(f'{month}零售额预测 (2003: {predictions[0]:.2f}亿元)')plt.xlabel('年份')plt.ylabel('零售额 (亿元)')plt.xticks(years + [2003])plt.legend()plt.grid(True, linestyle='--', alpha=0.7)plt.tight_layout()
plt.show()#汇总2003年预测结果
prediction_2003 = [monthly_predictions[month] for month in months]#创建结果DataFrame
result_df = df.copy()
result_df.loc[2003] = prediction_2003#绘制级比检验结果
plt.figure(figsize=(12, 8))
for i, month in enumerate(months):ratios = all_ratios[i]plt.plot(range(1998, 2003), ratios, 'o-', label=month)#添加级比值标签for j, ratio in enumerate(ratios):plt.text(1998 + j, ratio, f'{ratio:.2f}', fontsize=9,verticalalignment='bottom', horizontalalignment='center')#添加可容覆盖区间
n = len(years)
lower_bound = np.exp(-2 / (n + 1))
upper_bound = np.exp(2 / (n + 1))
plt.axhline(y=lower_bound, color='r', linestyle='--', alpha=0.7)
plt.axhline(y=upper_bound, color='r', linestyle='--', alpha=0.7)
plt.fill_between(range(1997, 2004), lower_bound, upper_bound, color='red', alpha=0.1)plt.title('级比检验结果 (1998-2002)')
plt.xlabel('年份')
plt.ylabel('级比值')
plt.xticks(range(1998, 2003))
plt.ylim(0.7, 1.5)
plt.legend(ncol=3, loc='upper right')
plt.grid(True, linestyle='--', alpha=0.5)
plt.show()# 绘制残差检验结果
plt.figure(figsize=(14, 10))
for i, month in enumerate(months):relative_errors = all_relative_errors[i]# 使用所有年份（包括第一年）years_with_errors = years  # 修改这里：使用完整年份列表plt.subplot(4, 3, i + 1)# 跳过第一个残差（通常为0），从第二个开始绘制plt.bar(years_with_errors[1:], relative_errors[1:], color='skyblue')plt.axhline(y=0.1, color='r', linestyle='--', label='10%阈值')# 添加残差值标签（跳过第一个）for j, error in enumerate(relative_errors[1:]):plt.text(years_with_errors[j + 1], error + 0.005, f'{error:.3f}',ha='center', fontsize=8)plt.title(f'{month}相对残差')plt.xlabel('年份')plt.ylabel('相对残差')plt.ylim(0, max(0.2, max(relative_errors[1:]) * 1.2))plt.legend()plt.grid(axis='y', linestyle='--', alpha=0.5)plt.tight_layout()
plt.show()#绘制级比偏差检验结果
plt.figure(figsize=(14, 10))
for i, month in enumerate(months):ratio_deviations = all_ratio_deviations[i]years_with_deviations = years[1:]  #级比偏差从第二年开始plt.subplot(4, 3, i + 1)plt.bar(years_with_deviations, ratio_deviations, color='lightgreen')plt.axhline(y=0.1, color='r', linestyle='--', label='0.1阈值')#添加级比偏差值标签for j, dev in enumerate(ratio_deviations):plt.text(years_with_deviations[j], dev + 0.005, f'{dev:.3f}',ha='center', fontsize=8)plt.title(f'{month}级比偏差')plt.xlabel('年份')plt.ylabel('级比偏差')plt.ylim(0, max(0.15, max(ratio_deviations) * 1.2))plt.legend()plt.grid(axis='y', linestyle='--', alpha=0.5)plt.tight_layout()
plt.show()#绘制2003年预测结果
plt.figure(figsize=(14, 7))
months_numeric = np.arange(1, 13)#绘制历史平均
historical_avg = df.mean(axis=0)
plt.plot(months_numeric, historical_avg, 'o--', color='gray', label='历史平均 (1997-2002)', alpha=0.7)#绘制2002年实际值
plt.plot(months_numeric, df.loc[2002], 'bo-', label='2002年实际值', markersize=8)#绘制2003年预测值
plt.plot(months_numeric, prediction_2003, 'ro-', label='2003年预测值', markersize=8)#添加数据标签
for i, month in enumerate(months):plt.text(months_numeric[i], prediction_2003[i], f'{prediction_2003[i]:.1f}',fontsize=9, verticalalignment='bottom', horizontalalignment='center')plt.text(months_numeric[i], df.loc[2002][i], f'{df.loc[2002][i]:.1f}',fontsize=9, verticalalignment='top', horizontalalignment='center')plt.title('2003年月度零售额预测 (单位:亿元)')
plt.xlabel('月份')
plt.ylabel('零售额 (亿元)')
plt.xticks(months_numeric, months)
plt.legend()
plt.grid(True, linestyle='--', alpha=0.5)plt.tight_layout()
plt.show()

这个题的思路就是对十二个月求十二次灰色预测，然后分别用这十二次的灰色预测求2003年该月的数据即可。

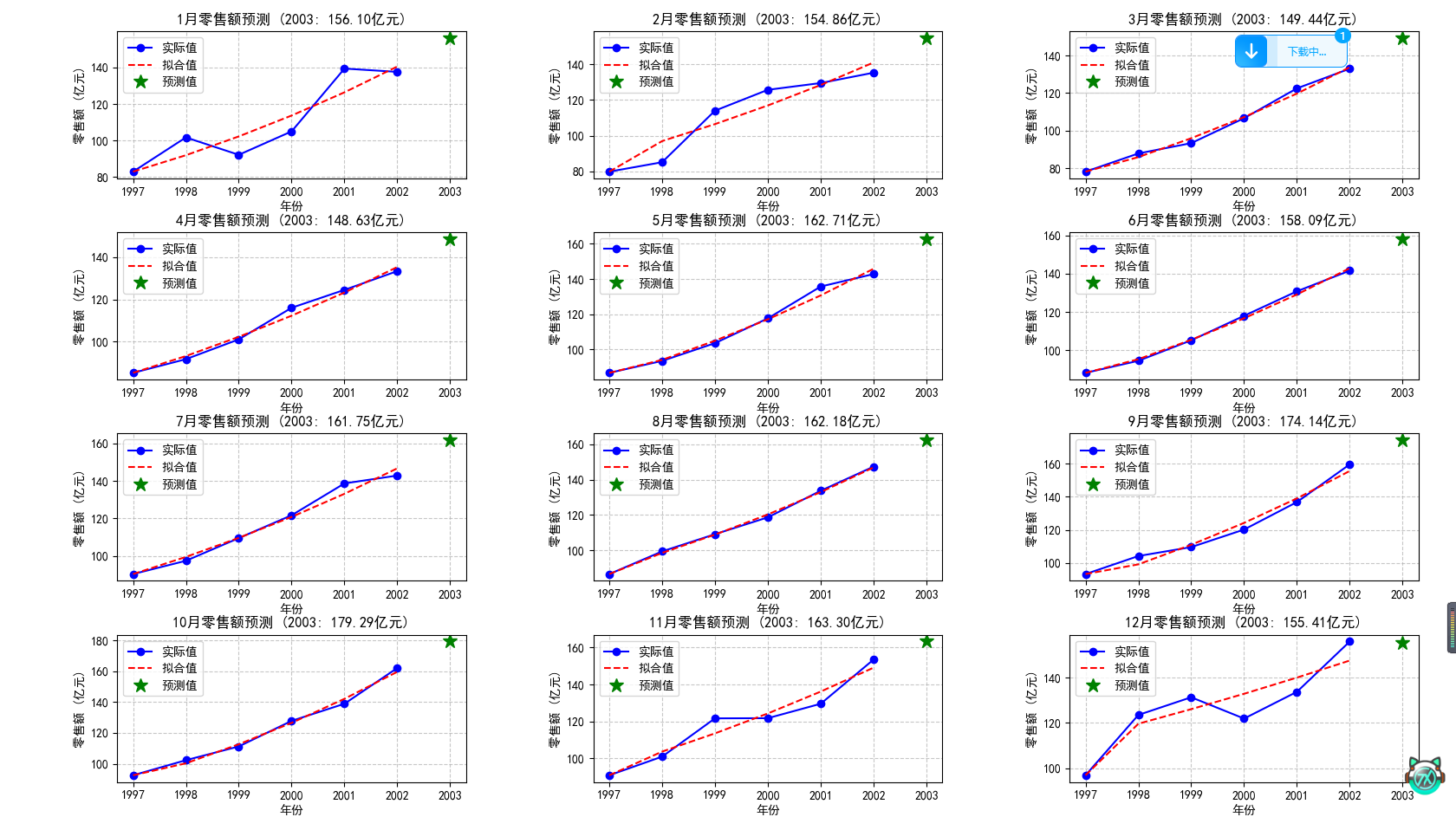
这就是预测出的图像。

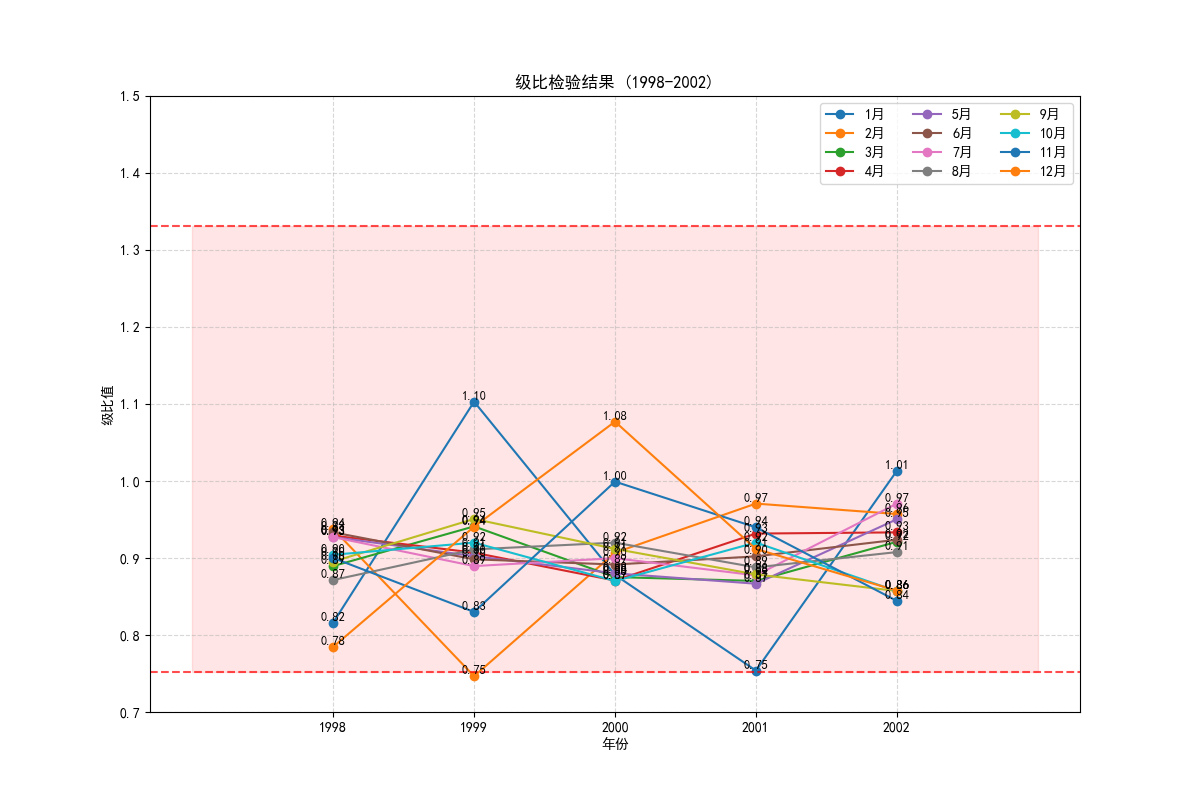
这是每年各月的级比检验结果，可以看出都挺适合用灰色预测的。

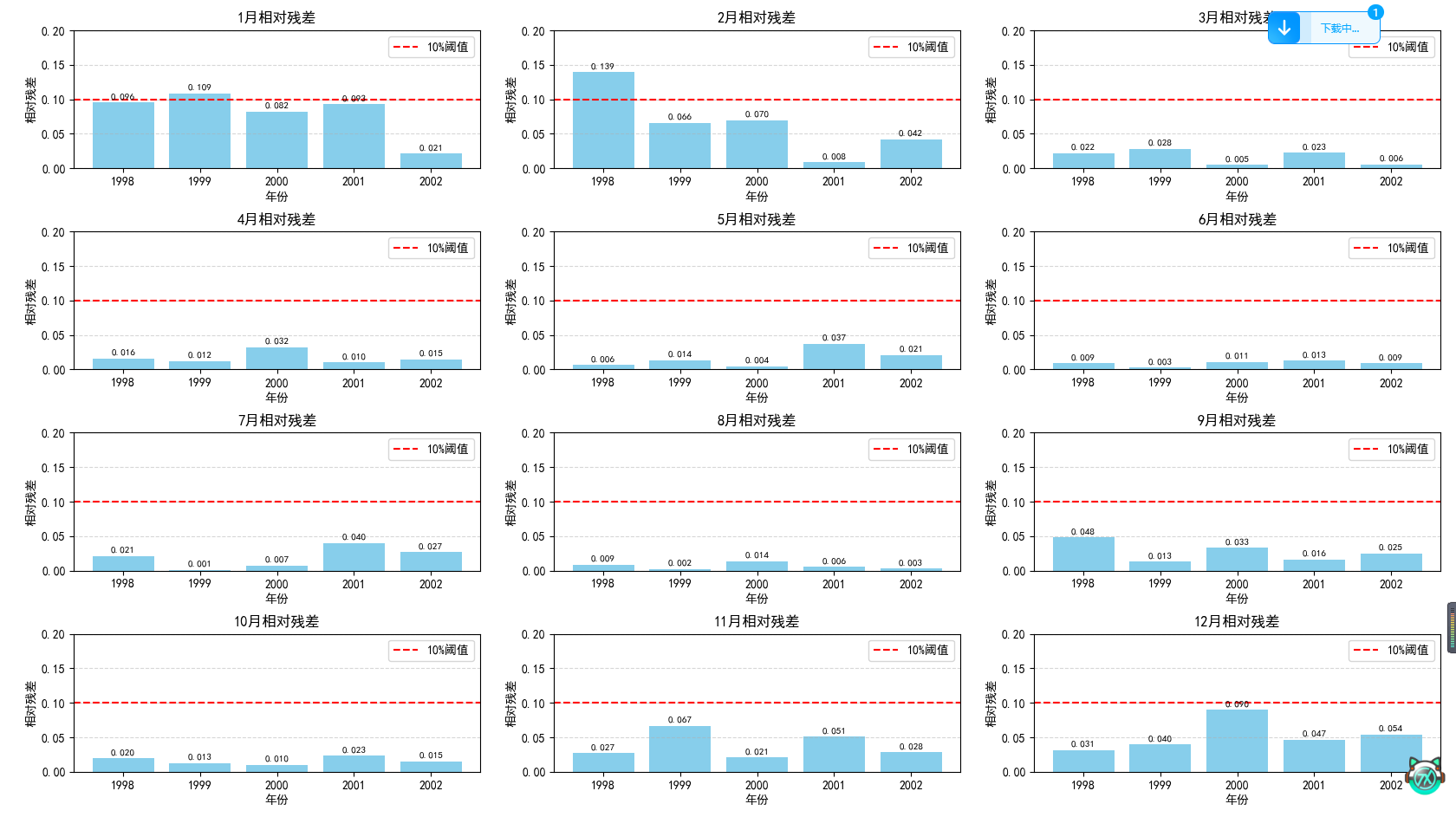
这是每个月的相对残差。

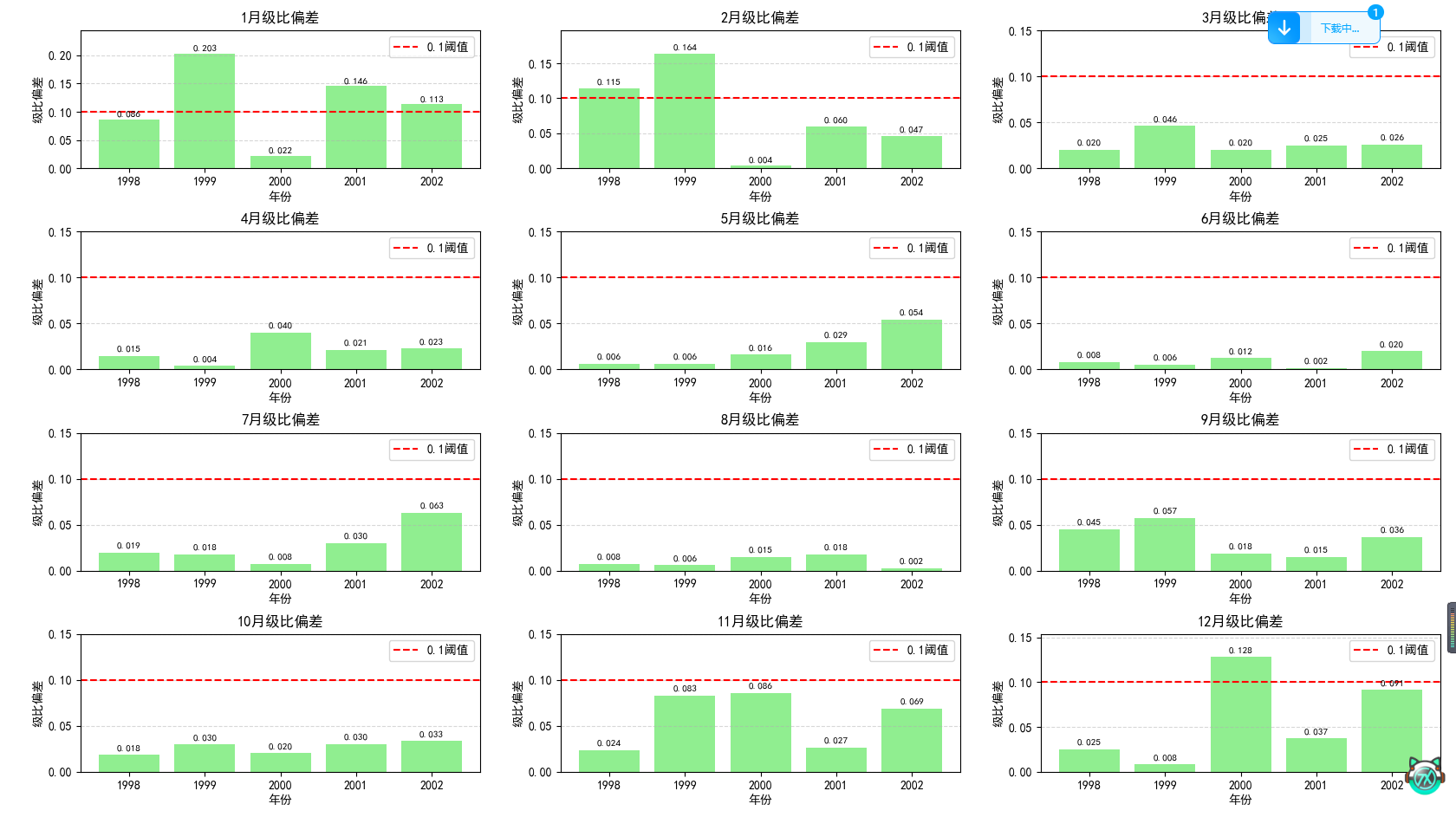
这是级比偏差。

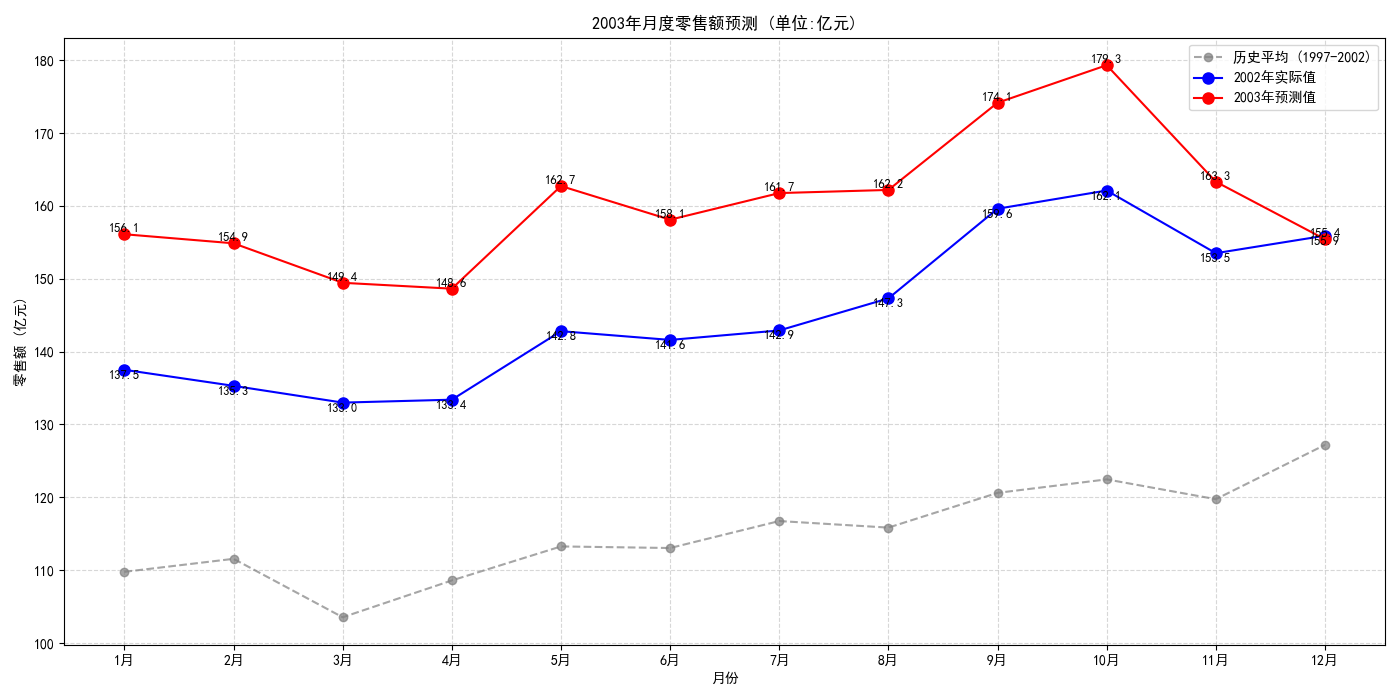
这个就是2003年每个月的折线图。

三、移动平均法和指数平滑法

草，原来真有这么个算法。

1.移动平均法

移动平均法非常简单粗暴，就是算出之前所有时间的平均值作为下一个时间的预测值。其中，这个值除了可以作为预测值，还可以作为描述当前状态的平滑值。其中，若想要更注重现在的时间，还可以对每个时间进行赋权，越靠近现在的权值越大然后计算加权平均值即可。

缺点也很明显，就是无法处理季节性的规律。

2.指数平滑法

指数平滑法就是在移动平均法的基础上，用权重量化了现在相比过去对未来的影响。换句话说，指数平滑法就是，每个时间点的权重会随着时间从现在到过去按指数规律递减。公式是，先定义平滑系数，那么新预测值就等于乘以最近时刻的实际值，加上乘以最近时刻的预测值。其中，越大说明现在的影响越大。

（这个公式怎么这么像dp）

很明显，这玩意儿也无法处理季节性规律。

四、ARIMA时间序列模型

1.基本概念

（1）时间序列

首先，时间序列很好理解，就是以时间顺序排列的数据所形成的序列。时间序列又分时期序列和时点序列，时期序列就是一段时间内的发展情况，时点序列就是时间内的情况。其中，时期序列可以累加，时点序列不能累加。举个例子，像中国历年GDP的数据就是时期序列，累加起来的意义就是多年里的GDP总和。而像某个人每年过生日时的身高就是时点序列，累加起来就没有意义。

（2）ARIMA模型

首先，ARIMA(p,q,d)分为自回归模型AR(p)，移动平均模型MA(q)和差分(d)。自回归模型AR(p)用于描述当前值和历史值的关系，其中的p表示选择之前p个历史数据。移动平均模型关注的就是自回归模型中误差项的累计，可以消除预测中的随机波动。注意这里的移动平均模型和上面的移动平均法无关！这里，将两者结合就是自回归移动平均模型ARMA(p,q)。之后，由于ARMA要求时间序列为平稳的，而一般情况中都是不平稳的时间序列，如呈现出一定的上升下降或季节性，所以需要使用差分法将非平稳的时间序列转化成平稳的时间序列，其中d为需要做的差分阶数，一般最多取到二阶即可。

（3）平稳性

这里再说明一下平稳性。平稳性就是意味着时间序列的均值和方差不发生明显变化，又分为严平稳和宽平稳。严平稳要求时间序列所有的统计特性都不会变化，宽平稳只要求均值，方差不变，且当前值只依赖过去值即可。实际情况中，基本上都是宽平稳即可，不存在严平稳。

（4）自相关系数ACF和偏自相关系数PACF

自相关系数可以反映当前时刻的数据与之前第k个时刻的数据整体的相关性，其范围为[-1,1]，大于0表示正相关，小于0表示负相关。要注意的是，这种关联既包括第k个历史时刻直接对当前时刻的影响，也包括从第k个历史时刻依次传递到当前时刻的影响。

偏自相关系数衡量的就是当前时刻与之前第k个时刻的直接关系，去除了沿着中间时刻传递过来的影响，其范围还是[-1,1]，含义如上。

由这个定义可以得知，不管是ACF还是PACF，如果是平稳序列，即不随时间变化，那么ACF和PACF的值一定会随着时间接近大幅下降直到接近零，这是因为随着时间推移过去对现在的影响一定越来越小。但如果是非平稳序列，那么自相关性会衰减得非常慢，这是因为存在趋势的影响，使得过去对现在有一个持久的影响。

（5）ADF检验

ADF检验就是判断一个时间序列是否平稳，这里同样需要计算p值。如果p值大于0.5，那就说明无法拒绝原假设，即不平稳，小于0.5,就说明平稳了。

（6）拖尾和截尾

拖尾就是序列的ACF或PACF值会缓慢缩小直到趋近于零，表明过去的影响会持续一段时间。截尾就是值突然下降到零且之后不恢复，表明过去的影响会在某时刻突然减小。

若从过去到现在，最后一个超出置信区间的值为过去第k个时刻，那就是k阶截尾或拖尾。

2.基本步骤

（1）平稳性检验

首先，需要对时间序列进行平稳性检验，判断是否需要进行差分，需要几阶差分。这里，最暴力的方法肯定就是直接看图，图像平稳那就是平稳。如果要量化的话，那就是用ADF检验。除此之外，其实还可以生成ACF的图像，通过是否在置信区间内判断是否平稳。

（2）确定p和q

确定p和q的方法也很简单粗暴。如果ACF和PACF均拖尾，那就用ARMA(p,q)模型。如果ACF截尾PACF拖尾，那就用MA(q)模型。如果ACF拖尾PACF截尾，那就用AR(p)模型。否则，就说明序列本身不存在明显的自相关性，这个模型可能压根不适用。其中，参数p和q就是截尾或拖尾的阶数k，注意MA和AR的参数是由截尾决定的。

由于这个方法还是过去主观，所以还可以考虑使用AIC或BIC准则计算参数值。这里如果真要用这个方法的话，一般用BIC就行了，因为BIC更准确。

（3）模型检验

检验这个模型是否效果良好，可以考虑画出残差的ACF图，如果落在置信区间内就说明效果良好。

3.练习

import numpy as np
import matplotlib.pyplot as plt
#ADF检验
from statsmodels.tsa.stattools import adfuller
#绘制ACF和PACF图像
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
#ARIMA模型
from statsmodels.tsa.arima.model import ARIMA
import pandas as pd
#使用中文字体
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False#生成随机数据
def generate_sample_data():np.random.seed(42)time = np.arange(60)base = 50 + 0.5 * timeseasonality = 10 * np.sin(time * 2 * np.pi / 12)noise = np.random.normal(0, 5, len(time))data = base + seasonality + noisereturn pd.Series(data, index=pd.date_range('2020-01-01', periods=60, freq='M'))#加载数据
ts = generate_sample_data()#绘制原始数据
plt.figure(figsize=(12, 6))
plt.plot(ts)
plt.title('原始时间序列数据')
plt.grid(True)
plt.show()#平稳性检验
def test_stationarity(timeseries):#ADF检验dftest = adfuller(timeseries, autolag='AIC')dfoutput = pd.Series(dftest[0:4], index=['Test Statistic', 'Lags Used', 'p-value', 'Number of Observations Used'])for key, value in dftest[4].items():dfoutput[f'Critical Value ({key})'] = valueprint("\nADF检验结果:")print(dfoutput)return dfoutput['p-value'] > 0.05  # 返回是否非平稳is_non_stationary = test_stationarity(ts)
print(f"数据是否非平稳: {is_non_stationary}")#确定差分阶数
def determine_d(data):d = 0current_data = data.copy()#检查原始数据是否平稳if not test_stationarity(current_data):print(f"原始数据平稳，推荐差分阶数 d = {d}")return d#原始数据非平稳，开始差分d = 1current_data = data.diff().dropna()while test_stationarity(current_data) and d < 2:  #最大差分2阶d += 1current_data = current_data.diff().dropna()print(f"\n推荐差分阶数 d = {d}")return dd = determine_d(ts)#绘制差分后数据
diff_data = ts.diff(d).dropna()
plt.figure(figsize=(12, 6))
plt.plot(diff_data)
plt.title(f'经过{d}阶差分后的时间序列')
plt.grid(True)
plt.show()#绘制ACF和PACF图
plot_acf(diff_data, lags=20,title='ACF图像')
plot_pacf(diff_data, lags=20,method='ywm',title='PACF图像')#使用BIC准则确定p和q
def find_best_arima(data, d, max_p=3, max_q=3):best_bic = float('inf')best_order = (0, d, 0)results = []for p in range(max_p + 1):for q in range(max_q + 1):if p == 0 and q == 0:continuetry:model = ARIMA(data, order=(p, d, q))model_fit = model.fit()bic = model_fit.bicresults.append((p, q, bic))if bic < best_bic:best_bic = bicbest_order = (p, d, q)except:continueprint("\n模型选择结果:")print(f"{'p':>3}{'q':>3}{'BIC':>10}")for r in results:print(f"{r[0]:3d}{r[1]:3d}{r[2]:10.2f}")print(f"\n最佳模型: ARIMA{best_order} (p,d,q)(BIC={best_bic:.2f})")return best_orderp, d, q = find_best_arima(ts, d)#拟合最终模型
model = ARIMA(ts, order=(p, d, q))
model_fit = model.fit()
print("\n模型摘要:")
print(model_fit.summary())#绘制残差的ACF图
residuals = model_fit.resid
plot_acf(residuals, lags=20,title='残差 ACF 图像')#预测
forecast_steps = 12
forecast = model_fit.get_forecast(steps=forecast_steps)
forecast_mean = forecast.predicted_mean
conf_int = forecast.conf_int()#绘制预测结果
plt.figure(figsize=(12, 6))
plt.plot(forecast_mean, label='预测数据', color='red')
plt.fill_between(conf_int.index,conf_int.iloc[:, 0],conf_int.iloc[:, 1],color='pink', alpha=0.3)
plt.title(f'ARIMA({p},{d},{q}) 预测(p,d,q)')
plt.legend()
plt.grid(True)
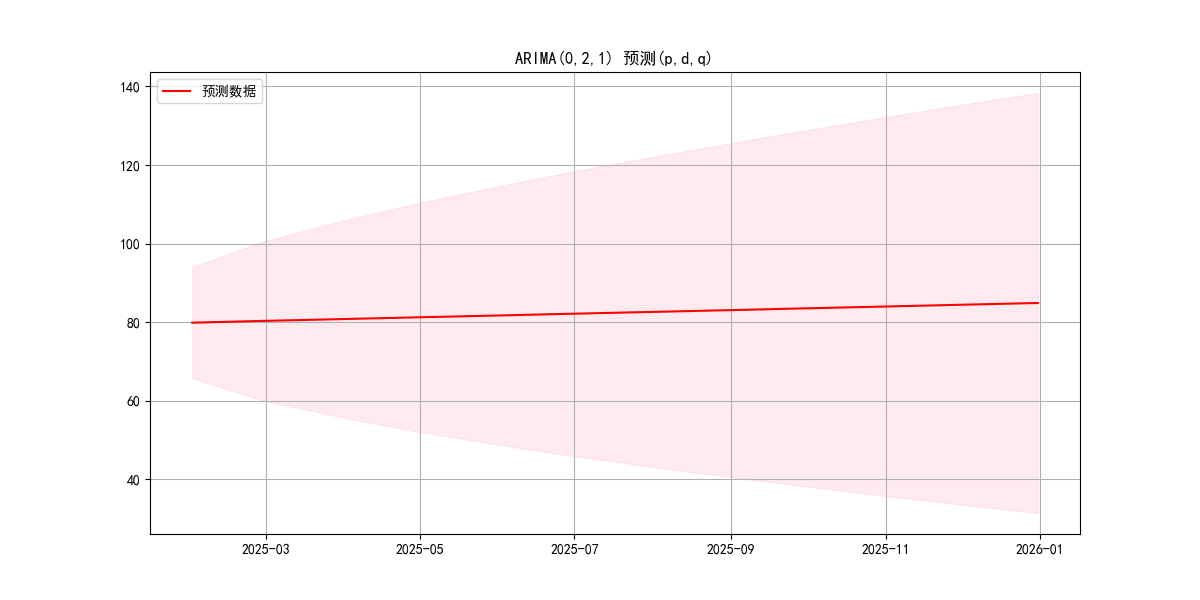
plt.show()

这随机的数据太邪门了，差分好几次p值都不满足条件。

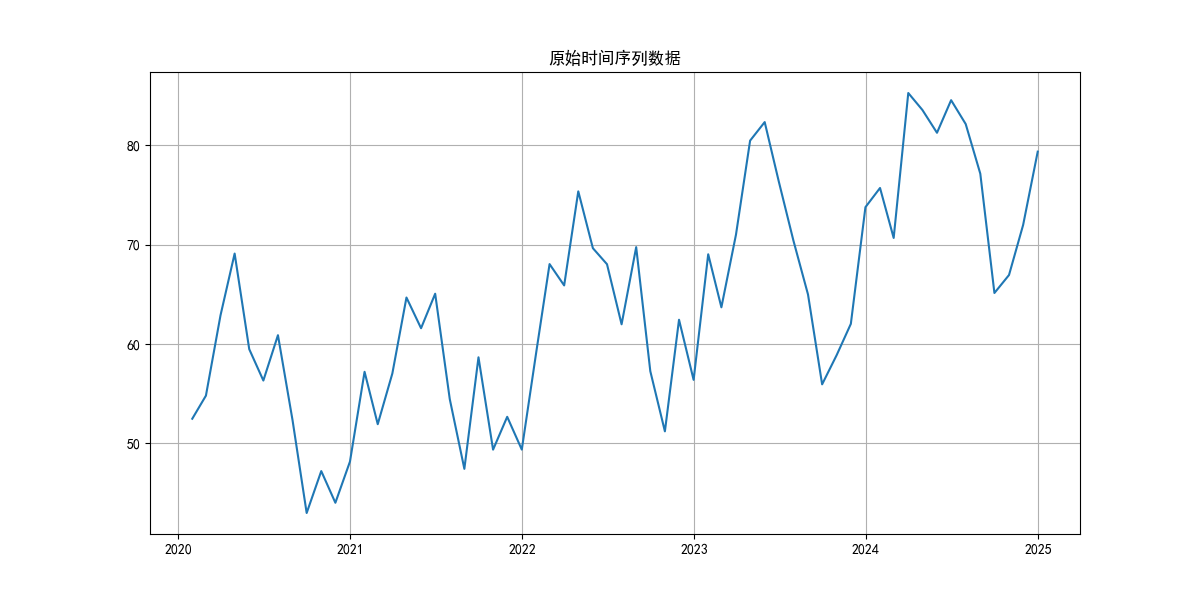
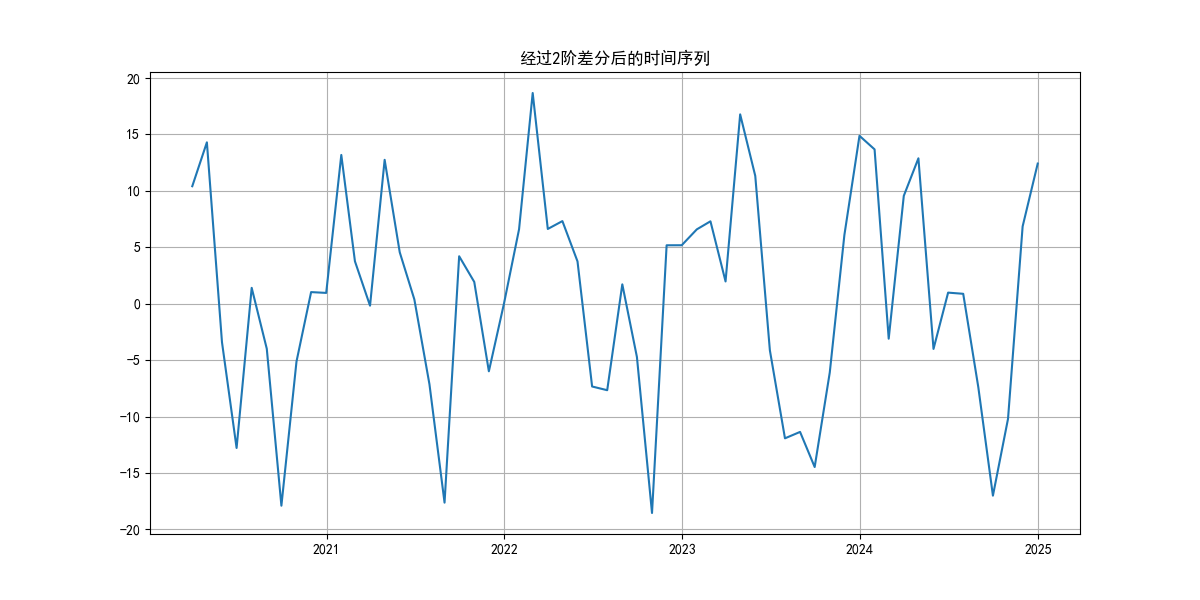
能看出来这数据真太烂了救不了一点……

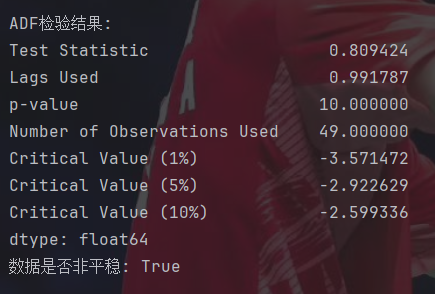
这里，第一行的数据代表T检验的值，第三行就是p值，后面三个1%，5%和10%代表的是不同程度拒绝原假设的值。判断时就是拿第一行的值和这几个值比较，小于的话就说明可以非常好地拒绝原假设。

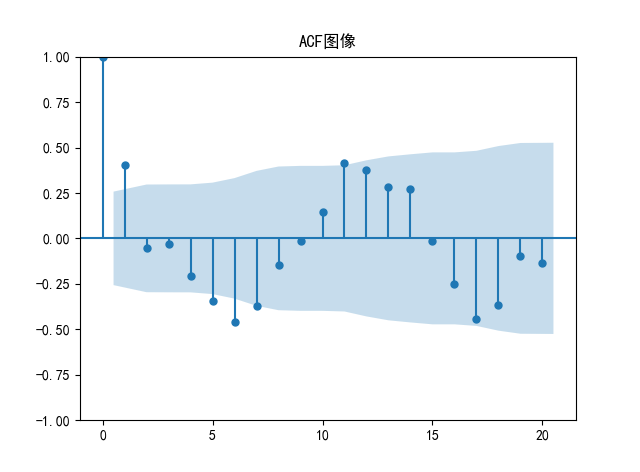
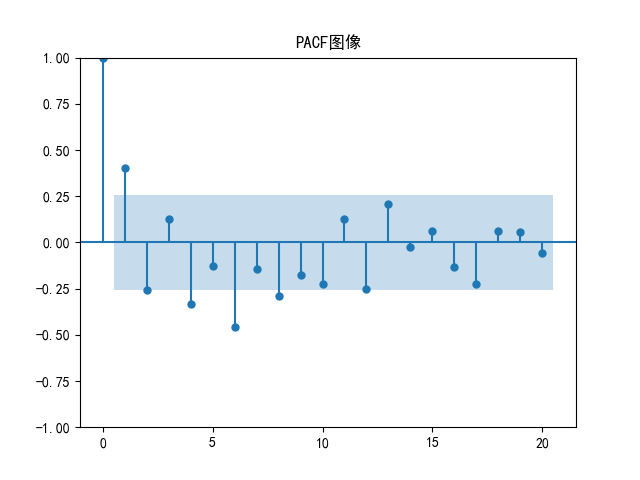
主观判断的话，ACF就是拖尾，PACF就是2阶截尾。

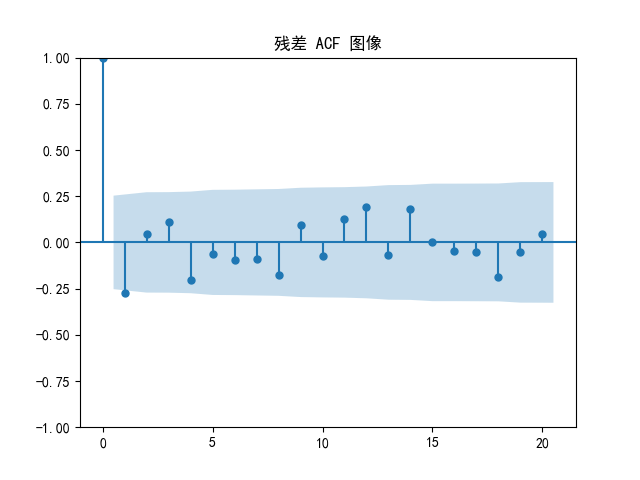
残差ACF倒挺正常的。

五、季节指数预测模型

1.基本概念

季节指数预测模型特别适用于预测有明显季节性波动的时间序列。

季节模型假设时间序列由长期趋势（T），季节变动（S），循环变动（C）和不规则变动（I）组成。长期趋势代表时间序列整体上是上升还是下降，季节变动就是由季节或气候引起的周期固定且重复出现的波动，而循环变动就是周期通常在一年以上且周期不固定的变动，不规则变动就是由偶然事件引起的变动。通常情况下，季节模型就是由这四个变量相乘得到。

之后，季节指数（SI）的定义为，在剔除了趋势，循环和不规则变动后，某个季节的数据相对于整体时间序列的平均值比例。举个例子，假如夏季冰激凌的销量的季节指数为1.25，那么说明在排除了长期趋势后，夏季冰激凌的销量为全年平均水平的125%，即比全年平均水平高出25%。注意，这里的季节不是指现实生活里的季节，而是存在周期性规律的周期，可以是一个季度，也可以是一个月。

2.基本步骤

首先，需要计算移动平均值。移动平均值的求法可以看作建立一个长度为一个完整季节周期长度的滑动窗口，然后在滑动的过程中每次计算窗口内的平均值。举个例子，假如以季节为一个完整的季节周期，那么就是计算4项的移动平均。所以对于1~4季度的移动平均值就将其放在第2和第3季度之间，2~5季度的移动平均值就将其放在第3和第4季度之间。而由于都在两季度之间，所以还要求居中移动平均值（CMA），那就是取相邻的两个移动平均值再求平均，与原始的季度对齐。

之后，需要计算季节比率（SR），就是用原始数据值除以这个居中移动平均值，剔除了趋势和循环成分。

然后就要消除不规则变动的影响，方法就是对所有同季度的季节比率求平均。由于这样求出来的这个平均值通常不会恰好等于1，所以要对季节指数进行调整。方法就是先计算调整因子（AF），如果要求的季节指数以1为平均水平，那么调整因子就是1除以总平均值。之后再用每个未调整的季节指数乘以调整因子即可。

最后，在确定需要预测哪个季节后，就需要计算趋势预测值。方法就是对于居中移动平均值序列，可以考虑使用移动平滑法、线性回归法或者指数平滑法求出趋势预测值。之后再用要预测的这个季节的季节指数乘以趋势预测值即可。

3.练习

import pandas as pd
import numpy as np#原始数据
data = {'Year': [2018,2018,2018,2018,2019,2019,2019,2019,2020,2020,2020,2020,2021,2021,2021,2021],'Quarter': [1,2,3,4,1,2,3,4,1,2,3,4,1,2,3,4],'Sales': [112,88,136,120,115,95,142,128,120,98,150,135,125,105,158,142]
}#创建DataFrame
df = pd.DataFrame(data)
df['Period'] = df['Year'].astype(str) + 'Q' + df['Quarter'].astype(str)#计算居中移动平均值（CMA）
period = 4  #季度数据周期为4 -> 窗口长度
ma = df['Sales'].rolling(window=period, min_periods=period).mean()
df['MA'] = ma.shift(-2)  #中心化对齐#计算季节比率
df['Seasonal_Ratio'] = df['Sales'] / df['MA']#计算未调整的季节指数
#按季度分组计算平均值
unadjusted_seasonal_index = df.groupby('Quarter')['Seasonal_Ratio'].mean().reset_index()
unadjusted_seasonal_index.columns = ['Quarter', 'Unadjusted_Index']#计算调整因子AF
#计算未调整季节指数的平均值
mean_unadjusted = unadjusted_seasonal_index['Unadjusted_Index'].mean()
#调整因子 = 1 / 未调整季节指数的平均值
adjustment_factor = 1 / mean_unadjusted#调整季节指数
unadjusted_seasonal_index['Adjusted_Index'] = unadjusted_seasonal_index['Unadjusted_Index'] * adjustment_factor#将调整后的季节指数合并回主表
df = df.merge(unadjusted_seasonal_index[['Quarter', 'Adjusted_Index']], on='Quarter')#计算趋势预测值 -> 移动平均法
#提取最后4个可用的CMA值作为基础
last_ma = df['MA'].dropna().tail(4).values
#计算平均增长量作为趋势变化
#至少有两个值才能进行差分
trend_change = np.diff(last_ma).mean() if len(last_ma) > 1 else 0#预测未来4个季度
forecast_periods = 4
last_actual_period = df['Period'].iloc[-1]
last_ma_value = last_ma[-1]#创建预测数据框
forecast_df = pd.DataFrame({'Period': [f'Forecast-Q{i}' for i in range(1, forecast_periods+1)],'Quarter': [1,2,3,4],'Trend_Forecast': [last_ma_value + (i+1)*trend_change for i in range(forecast_periods)]
})#合并季节指数
forecast_df = forecast_df.merge(unadjusted_seasonal_index[['Quarter', 'Adjusted_Index']], on='Quarter')#计算最终预测值
forecast_df['Sales_Forecast'] = forecast_df['Trend_Forecast'] * forecast_df['Adjusted_Index']#输出结果
print("原始数据与中间计算：")
print(df[['Period', 'Sales', 'MA', 'Seasonal_Ratio', 'Adjusted_Index']])print("\n未调整的季节指数：")
print(unadjusted_seasonal_index[['Quarter', 'Unadjusted_Index']])print("\n调整后的季节指数：")
print(unadjusted_seasonal_index[['Quarter', 'Adjusted_Index']])print("\n调整因子(AF):", round(adjustment_factor, 4))
print("调整后季节指数的平均值:", round(unadjusted_seasonal_index['Adjusted_Index'].mean(), 6))print("\n预测结果：")
print(forecast_df[['Period', 'Trend_Forecast', 'Adjusted_Index', 'Sales_Forecast']])#可视化结果
import matplotlib.pyplot as plt
#使用中文字体
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = Falseplt.figure(figsize=(12, 6))
#历史销量
plt.plot(df['Period'], df['Sales'], 'bo-', label='实际值')
plt.plot(df['Period'], df['MA'], 'g--', label='移动平均线')
#预测值
plt.plot(forecast_df['Period'], forecast_df['Sales_Forecast'], 'rs--', label='预测值')
#历史趋势线
plt.plot(df['Period'], df['MA'], 'g--', alpha=0.5)
#预测趋势线
plt.plot(forecast_df['Period'], forecast_df['Trend_Forecast'], 'm:', label='预测趋势线')
plt.title('季节指数预测')
plt.xlabel('时间')
plt.ylabel('销量')
plt.legend()
plt.grid(True)
plt.xticks(rotation=45)
plt.tight_layout()
plt.show()

季节指数预测模型倒挺简单的。

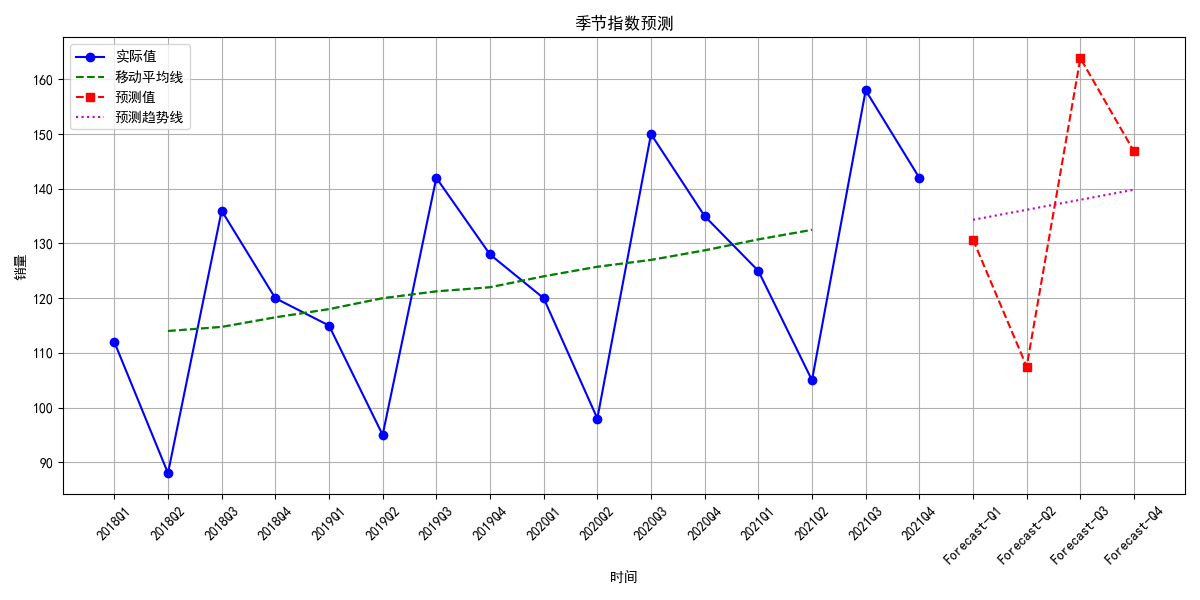
这个就是按季度划分。

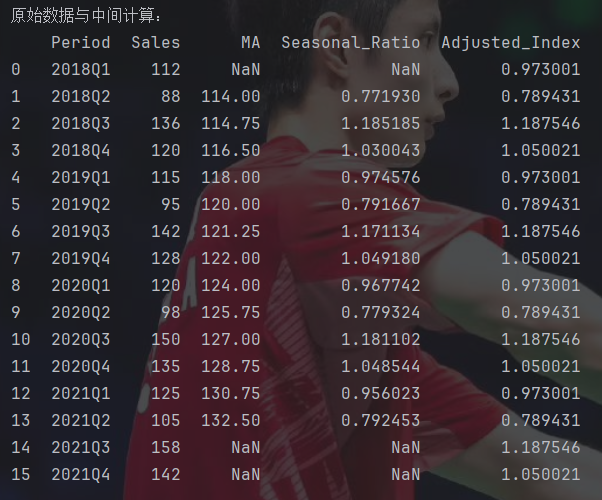
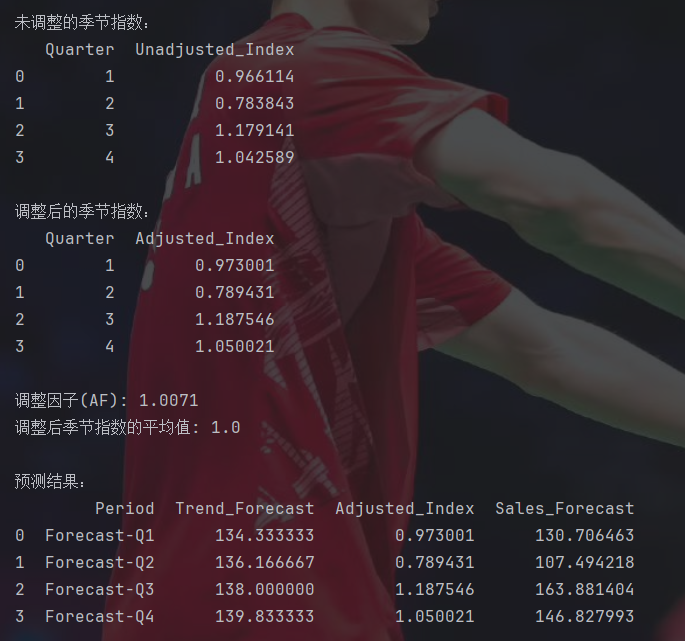
这组数据也挺特殊的，没调整的季节指数就能这么接近1。

六、马尔科夫模型

byd上学期看的线性代数网课全还给教授了。

1.基本概念

马尔科夫模型最核心的思路就是未来只取决于现在而不取决于过去，用dp的语言说，就是这是一个一阶的动态规划，即只依赖上一个状态。

再解释一下马尔科夫链中转移概率的齐次性，意思是，假如从当前时刻t的状态i转移到下一个时刻的状态j的概率为p，那么这个概率p不随时间而变化。进一步说，就是这个概率只和要当前时刻和要转移去的时刻有关。而将这些概率写成矩阵形式就能得到转移概率矩阵，假设一共有n个状态，那么这个转移概率矩阵就是一个n×n的方阵。所以，该矩阵的每个元素都大于等于0，而且每一行之和必然等于1，即从一个状态一定会转移到某个状态。所以，只要有了初始处于每个状态的概率分布，也就是初始为某个状态的概率，那么通过矩阵快速幂就能求出之后第k个时刻处于每个状态的概率。

对于转移概率矩阵的求法其实也非常暴力。若是给定了一系列的状态情况，那么就可以统计出由第i个状态转移到第j个状态的发生次数，那么再除以所有从第i个状态转移出去的总数就是第i个状态转移到第j个状态的概率。

2.练习

import numpy as np#原始天气数据
data = ['Sunny', 'Sunny', 'Rainy', 'Cloudy', 'Rainy', 'Sunny', 'Cloudy', 'Cloudy', 'Rainy', 'Sunny','Sunny', 'Cloudy', 'Cloudy', 'Rainy', 'Rainy', 'Sunny', 'Cloudy', 'Cloudy', 'Sunny', 'Sunny'
]#定义状态
states = ['Sunny', 'Cloudy', 'Rainy']
state_to_index = {state: i for i, state in enumerate(states)}#初始化转移计数矩阵
trans_counts = np.zeros((len(states), len(states)))#根据历史数据计算转移次数
for i in range(len(data) - 1):current_state = data[i]next_state = data[i + 1]#a[i][j] -> 从第j个状态转移到第i个状态trans_counts[state_to_index[next_state], state_to_index[current_state]] += 1#计算转移概率矩阵
trans_probs = trans_counts / np.sum(trans_counts, axis=0, keepdims=True)#打印转移概率矩阵
print("转移概率矩阵 (行: 次态, 列: 现态):")
print("      Sunny Cloudy Rainy")
for i, state in enumerate(states):probs = [f"{trans_probs[i, j]:.2f}" for j in range(len(states))]print(f"{state:6} {'  '.join(probs)}")#预测函数
def predict_next_states(current_state, n_steps=3):#初始状态向量current_vec = np.zeros(len(states))current_vec[state_to_index[current_state]] = 1.0#存储预测结果predictions = []#逐步预测for step in range(1, n_steps + 1):current_vec = trans_probs @ current_vec  #矩阵乘法更新状态predictions.append((step, dict(zip(states, current_vec))))return predictionsif __name__ == "__main__":#设置初始状态和预测步数current_weather = 'Rainy'n_steps = 3#预测predictions = predict_next_states(current_weather, n_steps)#打印结果print(f"\n初始状态: {current_weather}")for step, probs in predictions:print(f"\n预测 {step} 天后:")for state, prob in probs.items():print(f"  {state}: {prob:.2%}")#获取最可能状态most_likely = max(probs, key=probs.get)print(f"  最可能状态: {most_likely} (概率 {probs[most_likely]:.2%})")#可视化
import matplotlib.pyplot as plt
#使用中文字体
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = Falsedef plot_predictions(predictions):fig, ax = plt.subplots(figsize=(10, 6))days = [step for step, _ in predictions]for state in states:probs = [prob[state] for _, prob in predictions]ax.plot(days, probs, 'o-', label=state)ax.set_title('天气状态概率预测')ax.set_xlabel('预测天数')ax.set_ylabel('概率')ax.legend()ax.grid(True)plt.show()#生成预测图像
plot_predictions(predictions)

马尔可夫模型还是挺简单的，主要逻辑就是矩阵的累乘。

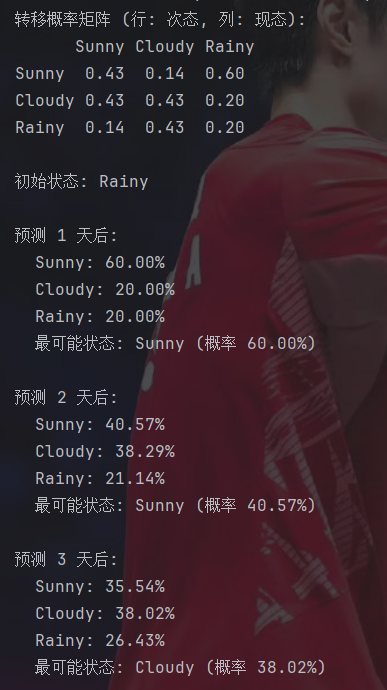
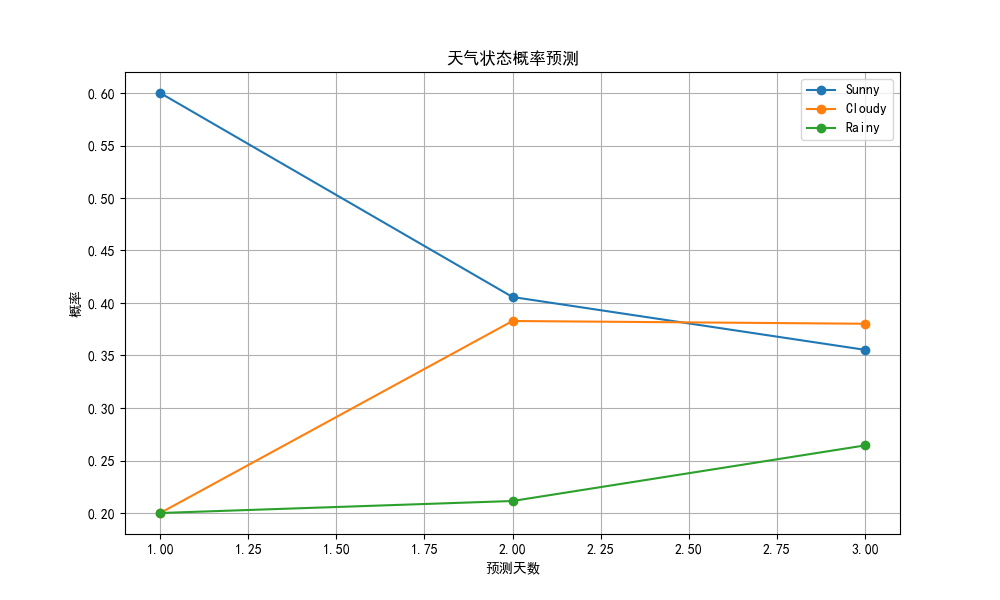
其实马尔可夫模型还有很多性质，如果之后有必要的话再说吧。

总结

时光时光慢些吧……感觉时间真不够用了……

END