当前位置：首页 > news >正文

C++-红黑树

news 2025/8/10 5:05:41

1、红黑树的概念

红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或 Black。通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

红黑树图像，如图所示：

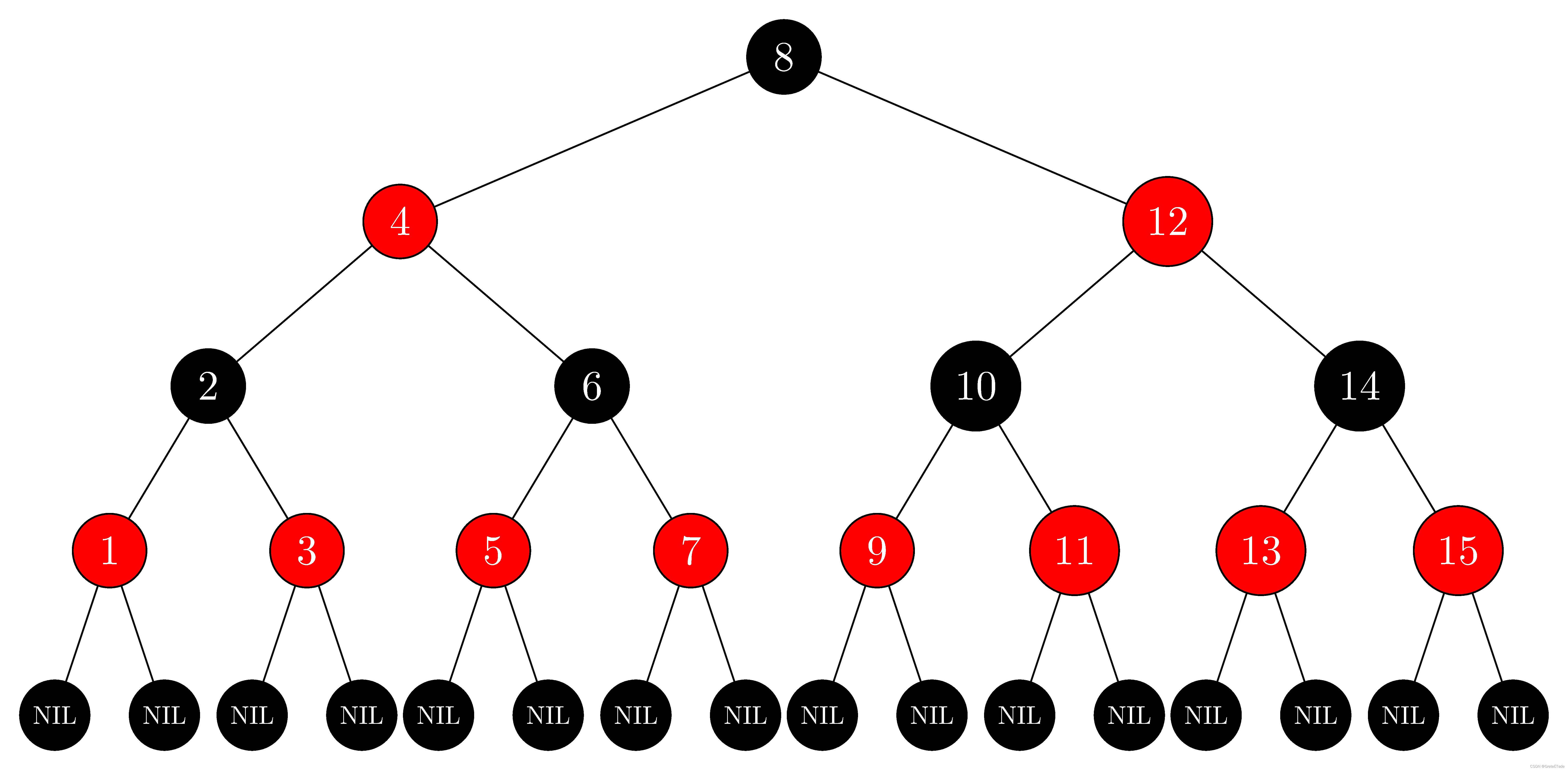
2、红黑树的性质

颜色属性：每个节点不是红色就是黑色
根节点属性：根节点必须是黑色的
红色节点属性：如果一个节点是红色的，则它的两个子节点必须是黑色的（即不能有两个连续的红色节点）
黑色高度属性：对于每个节点，从该节点到其所有后代叶节点的简单路径上，包含相同数目的黑色节点
叶子节点属性：每个叶子节点（NIL节点，空节点）都是黑色的

这些性质保证了红黑树的关键特性：最长路径不超过最短路径的两倍，从而保证了树的平衡性。

3、红黑树的实现

1.节点结构定义

template<class T>
struct RBTreeNode {RBTreeNode<T>* _left;    // 左子节点RBTreeNode<T>* _right;   // 右子节点RBTreeNode<T>* _parent;  // 父节点T _kv;                   // 键值对数据Colour _col;             // 节点颜色(RED或BLACK)RBTreeNode(const T& kv):_left(nullptr), _right(nullptr), _parent(nullptr),_kv(kv), _col(RED) {}
};

节点包含左右子节点指针、父节点指针、存储的数据以及颜色标记。新节点默认为红色。

2. 插入操作 (Insert)

功能：向红黑树中插入一个新节点，并保持红黑树的性质。

步骤：
如果树为空，创建新节点作为根节点，并设为黑色
按照二叉搜索树的规则找到插入位置
创建新节点（红色）并插入到正确位置
检查并修复红黑树性质：
如果父节点是黑色，无需处理
如果父节点是红色，需要调整：
情况1：叔叔节点是红色 - 变色处理
情况2：叔叔节点是黑色或不存在 - 旋转处理
确保根节点始终为黑色

约定:cur为当前节点，p为父节点，g为祖父节点，u为叔叔节点

情况一: cur为红，p为红，g为黑，u存在且为红

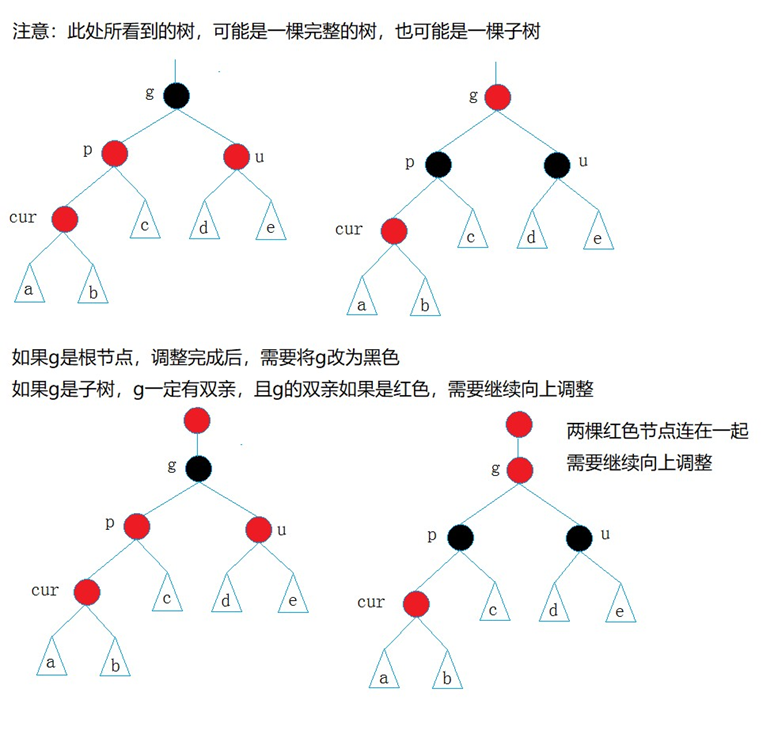
cur和p均为红，违反了性质三，此处能否将p直接改为黑？

解决方式：将p,u改为黑，g改为红，然后把g当成cur，继续向上调整。

情况二: cur为红，p为红，g为黑，u不存在/u存在且为黑

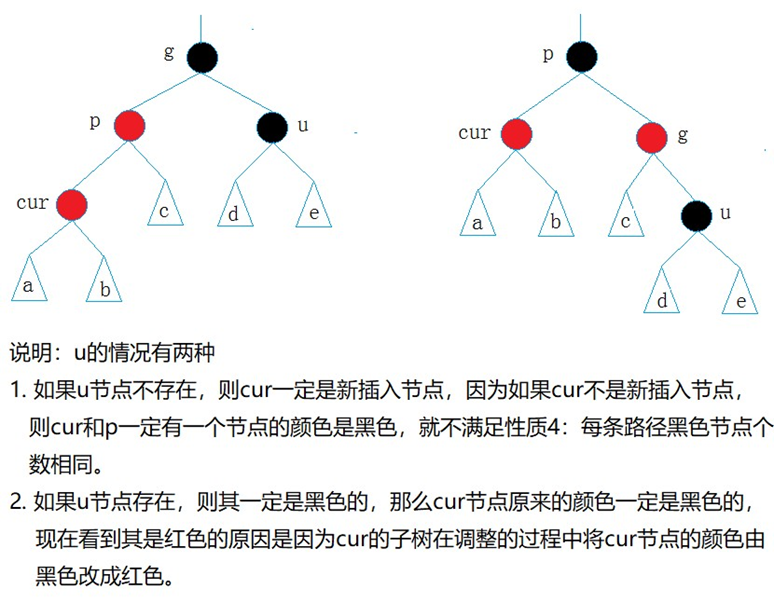
p为g的左孩子，cur为p的左孩子，则进行右单旋转；
相反， p为g的右孩子，cur为p的右孩子，则进行左单旋转
p、g变色--p变黑，g变红

情况三: cur为红，p为红，g为黑，u不存在/u存在且为黑

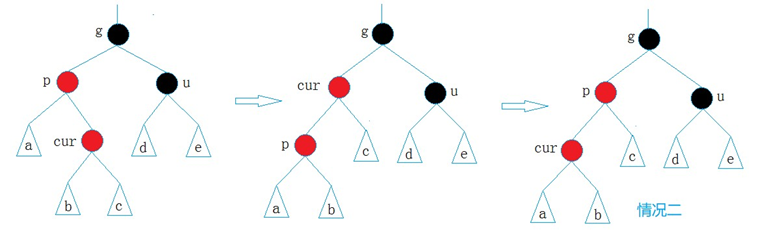
p为g的左孩子，cur为p的右孩子，则针对p做左单旋转；
相反， p为g的右孩子，cur为p的左孩子，则针对p做右单旋转
则转换成了情况2

针对每种情况进行相应的处理即可。

bool Insert(const T& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//u存在且为红if (uncle && uncle->_col == RED){//变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续向上处理cur = grandfather;parent = cur->_parent;}else //u不存在或存在且为黑{if (cur == parent->_left){//			g//		p//	cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//			g//		p//			cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else // parent == grandfather->_right{Node* uncle = grandfather->_left;//u存在且为红if (uncle && uncle->_col == RED){//变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续向上处理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){// g//	  p//       cRotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{// g//	  p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;
}

3. 左旋操作 (RotateL)

功能：以parent节点为支点进行左旋。

操作：
将cur的左子节点作为parent的右子节点
将parent作为cur的左子节点
更新各个节点的父指针
处理根节点情况

//左单旋
void RotateL(Node* parent)
{Node* cur = parent->_right;parent->_right = cur->_left;if (cur->_left){cur->_left->_parent = parent;}cur->_left = parent;Node* pparent = parent->_parent;parent->_parent = cur;if (pparent == nullptr){_root = cur;cur->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = cur;}else if (pparent->_right == parent){pparent->_right = cur;}cur->_parent = pparent;}
}

4.右旋操作 (RotateR)

功能：以parent节点为支点进行右旋。

操作：
将cur的右子节点作为parent的左子节点
将parent作为cur的右子节点
更新各个节点的父指针
处理根节点情况

//右单旋
void RotateR(Node* parent)
{Node* cur = parent->_left;parent->_left = cur->_right;if (cur->_right){cur->_right->_parent = parent;}Node* pparent = parent->_parent;cur->_right = parent;parent->_parent = cur;if (pparent == nullptr){_root = cur;cur->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = cur;}else{pparent->_right = cur;}cur->_parent = pparent;}
}

5. 红黑树验证 (IsBalance)

功能：验证红黑树是否满足以下性质：
每个节点要么是红色，要么是黑色
根节点是黑色
每个叶子节点（NIL节点）是黑色
不能有两个连续的红色节点
从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点

实现：
IsBalance()是公开接口，调用IsBalance(_root)
IsBalance(Node* root)验证根节点是否为黑色
CheckColour()递归检查：
计算每条路径的黑色节点数是否一致
检查是否有连续的红色节点

bool CheckColour(Node* root, int blacknum, int benchmark)
{//递归停止条件if (root == nullptr){if (blacknum != benchmark)return false;return true;}if (root->_col == BLACK){++blacknum;}if (root->_col == RED && root->_parent && root->_parent->_col == RED){cout << root->_kv.first << "出现连续的红色节点" << endl;return false;}return CheckColour(root->_left, blacknum, benchmark)&& CheckColour(root->_right, blacknum, benchmark);
}bool IsBalance()
{return IsBalance(_root);
}bool IsBalance(Node* root)
{if (root == nullptr)return true;if (root->_col != BLACK){return false;}//基准值int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)++benchmark;cur = cur->_left;}return CheckColour(root, 0, benchmark);
}

4、红黑树与AVL树的比较

特性	红黑树	AVL树
平衡标准	近似平衡（最长路径≤2倍最短）	严格平衡（高度差≤1）
查询效率	O(log n)	O(log n)
插入/删除效率	相对较高（旋转次数少）	相对较低（旋转次数多）
实现复杂度	中等	较高
适用场景	频繁插入删除的场景	查询为主、很少修改的场景