当前位置：首页 > news >正文

【感知机】感知机(perceptron)学习算法例题及详解

news 2025/8/9 19:52:38

感知机( perceptron )是二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取+1 和-1二值。感知机对应输入空间(特征空间)中将实例划分为正负两类的分离超平面，是一种判别模型。感知机是神经网络与支持向量机的基础
感知机学习旨在求出将训练数据进行线性划分的分离超平面。

感知机学习思路：
1.导入基于误分类的损失函数
2.利用梯度下降法对损失函数进行极小化
3.代入参数得到感知机模型。

感知机学习算法分类：
原始形式、对偶形式。

感知机算法原始形式例题及详解

例1 训练数据集如图所示，正实例点为 $x_1=(3,3)^{T}$ , $x_2=(4,3)^{T}$ ，负实例点为 $x_3=(1,1)^{T}$ ,试用感知机算法原始形式求感知机模型，令 $w=(w^{(1)},w^{(2)})^{T}$ , $x=(x^{(1)},x^{(2)})^{T}$

解答：

（1）建模最优化问题: $\underset{w,b}{min}L(w,b)= - \underset{x_i\in M}{\sum } y_i (w\cdot x_i+b )$

（2）取初值 $w_0=0,b_0=0$ ， $\eta =1$

（3）按 $x_1,x_2,x_3$ 顺序，对 $x_1=(3,3)^{T}$ , $y_1(w\cdot x1+b )= 0$ ，则 $x_1$ 为误分类点。更新 $w,b$ ：

$w_1=w_0+y_1x_1=(3,3)^{T}$ , $b_1=b_0+\eta y_1=1$

得到线性模型： $w_1\cdot x+b_1=3x^{(1)}+3x^{(2)}+1=0$

（4）重新选取，对 $x_1,x_2$ ， $y_i(w_1\cdot x_i+b_1)>0$ ，则均为正确分类点，不更新 $w,b$ ；

对 $x_3=(1,1)^{T}$ ， $y_3(w_1\cdot x_3+b_1)< 0$ ，则 $x_3$ 为误分类点，更新 $w,b$ ：

$w_2=w_1+y_3x_3=(2,2)^{T}$ , $b_2=b_1+\eta y_3=0$

得到线性模型： $w_2\cdot x+b_2=2x^{(1)}+2x^{(2)}=0$

（5）由此不断迭代

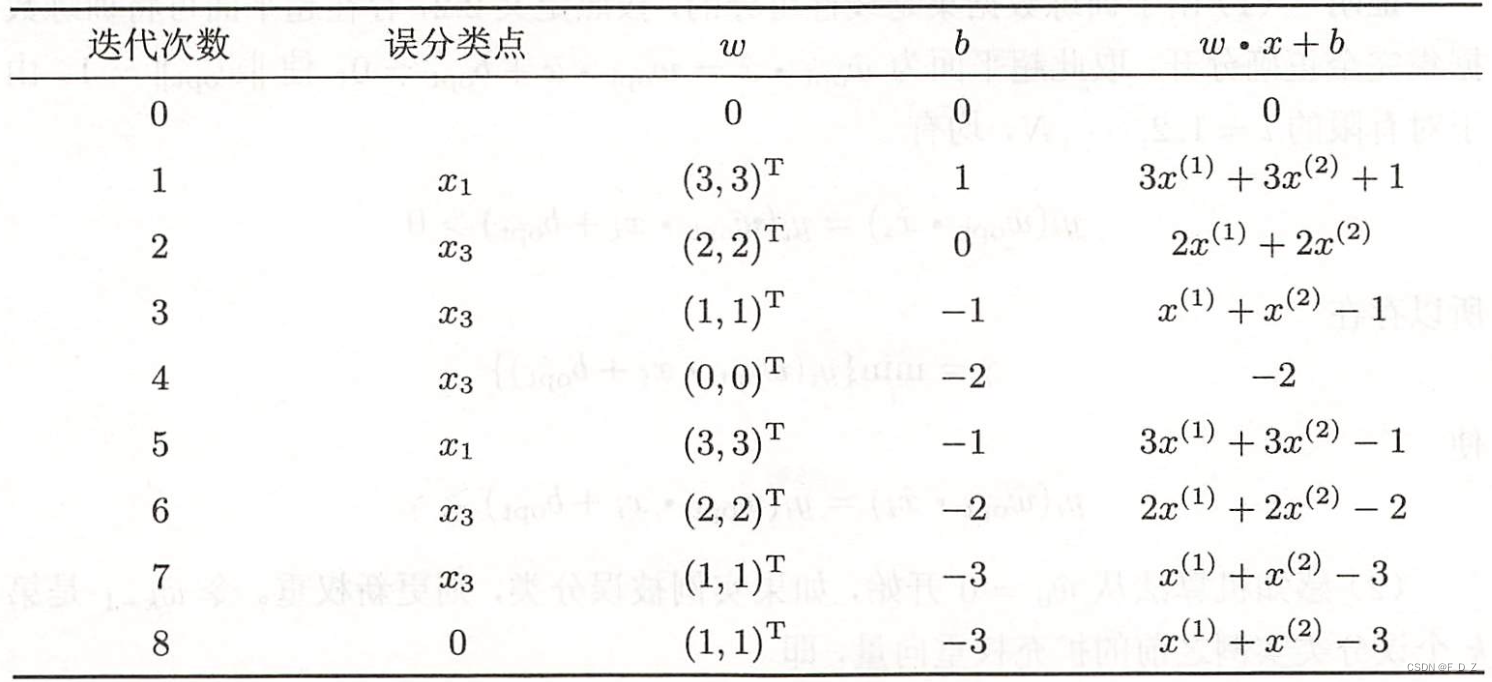
（6）直到 $w_7=(1,1)^{T}$ , $b_7=-3$

线性模型： $w_7\cdot x+b_7=x^{(1)}+x^{(2)}-3=0$

对所有数据点 $y_i(w_1\cdot x_i+b_1)>0$ ，则确定分离超平面： $x^{(1)}+x^{(2)}-3=0$

感知机模型 $f(x)=sign(x^{(1)}+x^{(2)}-3)$

分离超平面 $x^{(1)}+x^{(2)}-3=0$ 是按照 $x_1,x_3,x_3,x_3,x_1,x_3,x_3$ 的取点顺序得到的
例1如果更换取点顺序为 $x_1,x_3,x_3,x_3,x_2,x_3,x_3,x_3,x_1,x_3,x_3$ ，得到的分离超平面为：
$2x^{(1)}+x^{(2)}-5=0$
由此，可知结论：感知机算法采用不同的初值或选取不同的误分类点顺序，解可以不同

感知机算法对偶形式例题及详解

例2 训练数据集如图所示，正实例点为 $x_1=(3,3)^{T}$ , $x_2=(4,3)^{T}$ ，负实例点为 $x_3=(1,1)^{T}$ ,试用感知机算法对偶形式求感知机模型，令 $w=(w^{(1)},w^{(2)})^{T}$ , $x=(x^{(1)},x^{(2)})^{T}$

解答：

（1）取 $\alpha_1=0,i=1,2,3,b=0,\eta =1$ ;