当前位置：首页 > news >正文

深度学习（2）：自动微分

news 2025/8/8 13:24:23

自动微分模块torch.autograd负责自动计算张量操作的梯度，具有自动求导功能。自动微分模块是构成神经网络训练的必要模块，可以实现网络权重参数的更新，使得反向传播算法的实现变得简单而高效。

张量
Torch中一切皆为张量，属性requires_grad决定是否对其进行梯度计算。默认是 False，如需计算梯度则设置为True。
计算图：
torch.autograd通过创建一个动态计算图来跟踪张量的操作，每个张量是计算图中的一个节点，节点之间的操作构成图的边。
在 PyTorch 中，当张量的 requires_grad=True 时，PyTorch 会自动跟踪与该张量相关的所有操作，并构建计算图。每个操作都会生成一个新的张量，并记录其依赖关系。当设置为 True 时，表示该张量在计算图中需要参与梯度计算，即在反向传播（Backpropagation）过程中会自动计算其梯度；当设置为 False 时，不会计算梯度。

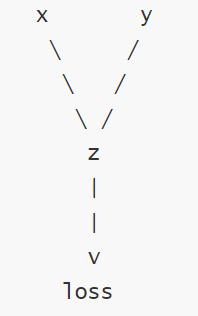
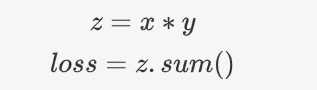
1、detach()：修改叶子节点

    t = torch.tensor([1, 2, 3], dtype=torch.float, requires_grad=True)t[0] = 10print(t)#会报错# 计算图中的叶子节点不允许直接修改# 如果要修改，使用detach()t1 = t.detach()t1[0] = 10print(t1)#tensor([10.,  2.,  3.])print(t)#tensor([10.,  2.,  3.], requires_grad=True)

2、y.backward()：反向传播，自动计算梯度

# 张量添加requires_grad属性，张量的数据类型需要时float
# 如果数据类型是整数，则报错
# RuntimeError: Only Tensors of floating point and complex dtype can require gradients
x = torch.tensor(2.0, requires_grad=True)
y = x ** 2# 反向传播，自动计算梯度
y.backward()

3、计算梯度

    x = torch.tensor([1, 2, 3], requires_grad=True, dtype=torch.float)y = x ** 2# z = y.sum()z = y.mean()# 反向传播默认输出是标量，如果输出值是向量可以在backward()进行梯度张量初始化# y.backward(torch.tensor([1.0, 1.0, 1.0]))z.backward()print(x.grad)#tensor([0.6667, 1.3333, 2.0000])

（1）、标量梯度计算

    x1 = torch.tensor(2, requires_grad=True, dtype=torch.float)x2 = torch.tensor(3, requires_grad=True, dtype=torch.float)y = x1**2 + x2**2y.backward()print(x1.grad, x2.grad)#tensor(4.) tensor(6.)

（2）、向量梯度计算

    x1 = torch.tensor([1,2,3], requires_grad=True, dtype=torch.float)x2 = torch.tensor([2,3,4], requires_grad=True, dtype=torch.float)y = x1**2 + 2*x2z = y.sum()z.backward()print(x1.grad, x2.grad)#tensor([2., 4., 6.]) tensor([2., 2., 2.])

4、控制梯度计算

    x = torch.tensor(5.0, requires_grad=True)# y默认也会参与梯度计算，但是不保存该梯度值# y = x**2# print(y.requires_grad)# torch.no_grad():设置不参与梯度计算with torch.no_grad():y = x**2print(y.requires_grad)

5、梯度清零

    x = torch.tensor([1, 2, 3], requires_grad=True, dtype=torch.float)# 默认情况下，叶子节点的梯度不会自动清零，会累加for epoch in range(5):y = x ** 2z = y.sum()# 自动清零# 目的：获取当前轮次的梯度，不是累加值if x.grad is not None:x.grad.zero_()z.backward()print(x.grad)
#tensor([2., 4., 6.])
#tensor([2., 4., 6.])
#tensor([2., 4., 6.])
#tensor([2., 4., 6.])
#tensor([2., 4., 6.])

6、通过梯度下降找到函数最小值

    # 初始化起始值x = torch.tensor(3.0, requires_grad=True)epochs = 50# 学习率lr = 0.1listx = []listy = []for epoch in range(epochs):y = x ** 2# 梯度清零if x.grad is not None:x.grad.zero_()# 反向传播，计算梯度y.backward()# 设置不参与梯度计算with torch.no_grad():# 梯度下降# x = x-lr*x.grad # x 为新变量x -= lr * x.grad  # x原地修改print(f'epoch: {epoch}, x: {x}')listx.append(x.item())listy.append(y.item())plt.scatter(listx, listy)plt.show()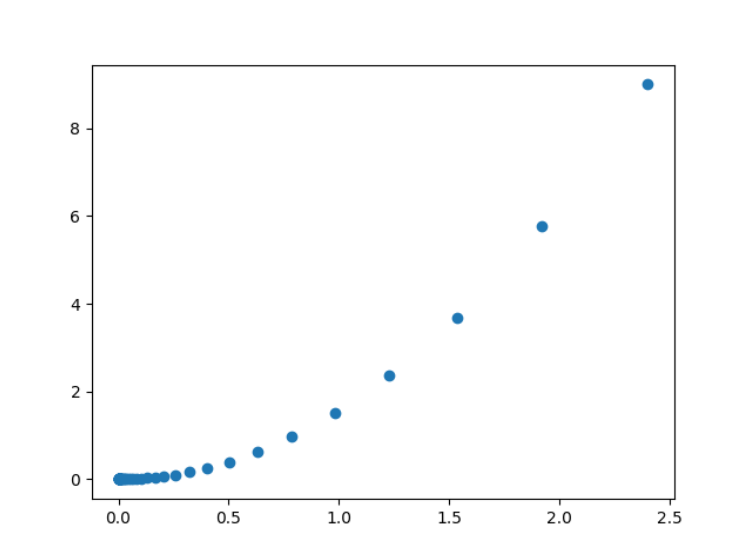

7、函数参数求解

import torch# 定义数据x = torch.tensor([1, 2, 3, 4, 5], dtype=torch.float)y = torch.tensor([3, 5, 7, 9, 11], dtype=torch.float)# 定义模型参数 a 和 b，并初始化a = torch.tensor([1], dtype=torch.float, requires_grad=True)b = torch.tensor([1], dtype=torch.float, requires_grad=True)# 学习率lr = 0.1# 迭代轮次epochs = 100for epoch in range(epochs):# 前向传播：计算预测值 y_predy_pred = a * x + b# 定义损失函数loss = ((y_pred - y) ** 2).mean()if a.grad is not None and b.grad is not None:a.grad.zero_()b.grad.zero_()# 反向传播：计算梯度loss.backward()# 梯度下降with torch.no_grad():a -= lr * a.gradb -= lr * b.gradif (epoch + 1) % 10 == 0:print(f'Epoch [{epoch + 1}/{epochs}], Loss: {loss.item():.4f}')print(f'a: {a.item()}, b: {b.item()}')

1、数据定义

2、模型参数初始化

3、超参数设置

4、训练循环

4.1、前向传播

使用当前的 a 和 b 计算预测值 y_pred

4.2、计算损失

损失函数衡量预测值与真实值的差距

这里使用均方误差（MSE）：先计算每个样本的误差平方，再取平均值

4.3、梯度清零

清除上一轮计算的梯度（PyTorch 会累积梯度，所以需要手动清零）

4.4、反向传播