KNN算法:从原理到实战应用
文章目录
- KNN(K-Nearest Neighbors)算法详解
- 1. 算法概述
- 2. 算法原理
- 2.1 基本流程
- 2.2 距离度量
- (1) 欧氏距离(最常用)
- (2) 曼哈顿距离
- (3) 闵可夫斯基距离(泛化形式)
- (4) 余弦相似度(文本向量场景常用)
- 2.3 决策规则
- 3. 算法实现
- 3.1 分类示例(`sklearn`)
- 3.2 决策边界可视化
- 4. 模型评估与超参数选择
- 5. 优缺点分析
- 5.1 优点
- 5.2 缺点
- 6. 维度灾难解析
- 7. 应用场景
- 8. 总结
KNN(K-Nearest Neighbors)算法详解
1. 算法概述
KNN 是一种 基于实例的监督学习算法,常用于分类和回归。核心思想是:
一个样本的类别/数值由其最近的 K 个邻居共同决定。
直观类比:想判断一个水果是苹果还是橙子?看看它周围最相似的 K 个水果是什么。
2. 算法原理
2.1 基本流程
- 选择超参数 KKK(邻居数量)。
- 计算新样本与训练集中所有样本的距离。
- 选取距离最近的 KKK 个样本。
- 分类任务:多数投票决定类别。
回归任务:取 K 个邻居的平均值。
2.2 距离度量
(1) 欧氏距离(最常用)
d(x,y)=∑i=1n(xi−yi)2d(\mathbf{x}, \mathbf{y}) = \sqrt{\sum_{i=1}^n (x_i - y_i)^2} d(x,y)=i=1∑n(xi−yi)2
(2) 曼哈顿距离
d(x,y)=∑i=1n∣xi−yi∣d(\mathbf{x}, \mathbf{y}) = \sum_{i=1}^n |x_i - y_i| d(x,y)=i=1∑n∣xi−yi∣
(3) 闵可夫斯基距离(泛化形式)
d(x,y)=(∑i=1n∣xi−yi∣p)1pd(\mathbf{x}, \mathbf{y}) = \left( \sum_{i=1}^n |x_i - y_i|^p \right)^{\frac{1}{p}} d(x,y)=(i=1∑n∣xi−yi∣p)p1
(4) 余弦相似度(文本向量场景常用)
cos(θ)=x⋅y∥x∥∥y∥\cos(\theta) = \frac{\mathbf{x} \cdot \mathbf{y}}{\|\mathbf{x}\|\|\mathbf{y}\|} cos(θ)=∥x∥∥y∥x⋅y
2.3 决策规则
- 分类:多数投票法
y^=argmaxc∑i=1KI(yi=c)\hat{y} = \underset{c}{\arg\max} \sum_{i=1}^K I(y_i = c) y^=cargmaxi=1∑KI(yi=c)
- 回归:均值法
y^=1K∑i=1Kyi\hat{y} = \frac{1}{K} \sum_{i=1}^K y_i y^=K1i=1∑Kyi
3. 算法实现
3.1 分类示例(sklearn)
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier# 1. 加载数据
X, y = load_iris(return_X_y=True)# 2. 数据划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42
)# 3. 特征标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)# 4. 训练 KNN 模型
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_train, y_train)# 5. 模型评估
print("测试集准确率:", knn.score(X_test, y_test))
3.2 决策边界可视化
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier# 仅使用两个特征绘制边界
X_plot = X[:, :2]
X_train, X_test, y_train, y_test = train_test_split(X_plot, y, test_size=0.3, random_state=42
)knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_train, y_train)# 网格化区域
x_min, x_max = X_plot[:, 0].min() - 1, X_plot[:, 0].max() + 1
y_min, y_max = X_plot[:, 1].min() - 1, X_plot[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),np.arange(y_min, y_max, 0.1)
)
Z = knn.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)# 绘图
plt.contourf(xx, yy, Z, alpha=0.3)
plt.scatter(X_plot[:, 0], X_plot[:, 1], c=y, edgecolors='k')
plt.title("KNN 决策边界")
plt.xlabel("特征1")
plt.ylabel("特征2")
plt.show()
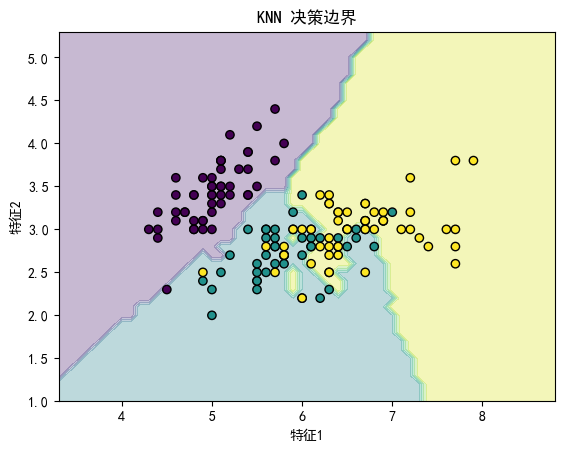
4. 模型评估与超参数选择
- K 值的影响
- KKK较小:模型复杂度高,易过拟合。
- KKK 较大:模型平滑,易欠拟合。
- 通常使用交叉验证选择最佳 KKK。
- 距离度量选择
- 特征量纲不同需先标准化/归一化。
5. 优缺点分析
5.1 优点
- 简单易实现
- 训练阶段无开销(是一种惰性训练)
- 可解决多分类问题
- 理论成熟,效果可靠
5.2 缺点
- 预测阶段计算量大(需计算所有样本的距离)
- 对特征缩放敏感
- 维度灾难(高维空间下邻居不再“近”)
6. 维度灾难解析
随着维度 ddd 增加:
- 数据在高维空间中变稀疏;
- 最近邻与最远邻的距离趋近于 0。
数学解释:
若数据均匀分布,当维度 ddd 增加时,为覆盖体积 vvv,超立方体边长需扩张为:r=(v)1/dr = (v)^{1/d}r=(v)1/d
当 d→∞,r→1d \to \infty,r \to 1d→∞,r→1,导致最近邻与所有点“几乎等距”。
7. 应用场景
- 图像识别(如手写数字识别)
- 基于相似度的推荐系统
- 文本分类(结合 TF-IDF 向量)
- 异常检测
8. 总结
- KNN 是基于“相似性”的懒惰学习算法;
- 超参数 KK 与距离度量对性能影响显著;
- 高维问题需结合 降维(如 PCA) 或特征选择。
