当前位置：首页 > news >正文

nflsoi 8.6 题解

news 2025/8/7 17:16:53

A.#2985 S数 / 洛谷 P1362

题意

设 $S (N)$ 表示 $N$ 十进制下各位数字之和。如果一个正整数满足 $S(x2)=S(x)×S(x)S(x^2) = S(x) \times S(x)$ ，我们称之为 Rabbit Number。

比如， $22$ 就是一个 Rabbit Number，因为 $\times S(22)$ 。

给出一个区间 $[L, R]$ ，求在该区间内的 Rabbit Number 的个数。

$\le L \le R \le 10^9$ 。

思路

根据打表可得：这些数每位数字都小于 $4$ 。

应该是因为大于等于 $4$ 的数平方会进位，使数字和减小，影响答案。即 $S(x2)≤S(x)×S(x)S(x^2)\le S(x)\times S(x)$ 。

这里上下界虽然大，但是十进制数位顶天 $9$ 位（ $10^9$ 不是兔子数）。于是我们可以 dfs 给每一位填 $0∼30\sim 3$ 。

对于已经填了前若干位的数 $c u r$ ，设 $x$ 表示 $c u r$ 后再填一位之后的数，我们判断 $x$ 是否为非零兔子数，如果其在 $[L, R]$ 之间就贡献 $+ 1$ 。时间复杂度为 $O(4^{10})$ 。

过掉这道题已经够了。不过还能优化：发现兔子数的数位任一前缀也是兔子数，若前缀不是兔子数，那么前缀平方的数字和就小于前缀数字和的平方，因为 $S(x2)≤S(x)×S(x)S(x^2)\le S(x)\times S(x)$ ，所以后面的数位肯定补不回来这个差值。所以说当 $x$ 不是兔子数就可以不用 $x$ 继续往下填数了。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
ll l,r;
ll cal(ll x)
{ll ret=0;while(x){ret+=x%10;x/=10;}return ret;
}
ll ans;
void dfs(ll cur)
{for(int i=0;i<4;i++){ll x=cur*10+i;if(x==0||cal(x)*cal(x)!=cal(x*x))continue;if(l<=x&&x<=r)ans++;if(x*10<=r)dfs(x);}
}
int main()
{freopen("snum.in","r",stdin);freopen("snum.out","w",stdout);scanf("%lld%lld",&l,&r);dfs(0);printf("%lld",ans);return 0;
}

B.#1827 字典序迷宫 / COCI 2016/2017 #3 Pohlepko

题意

Lay 博士现在有一个 $n×mn\times m$ 的字符迷宫,每个格子都有一个小写英语字母。其中，左上角记作 $(1, 1)$ ，右下角记作 $(n, m)$ 。

现在 Lay 博士站在 $(1, 1)$ ，终点为 $(n, m)$ ，迷宫规定只能往右或者往下走。

Lay 博士只有保证他从起点走到终点所得到的字符序列是字典序最小的才能够顺利走出迷宫，现在请帮助他求出字典序最小的序列。

思路

~~赛时又是非常唐，先是递推然后 bfs，再是用队列维护多个可选择的相同最优字母，最终 WA 20pts 不如 bfs MLE 70pts，看来黄绿题要重点突破了。~~下面讲一个我赛时想到的一个更清晰的做法。

注意到：走的格子数为 $n + m - 1$ ，每一步能走的各自构成 $n - m + 1$ 条 $45°$ 直线，直线上的点的行数加列数为步数减 $1$ ：
在这里插入图片描述
（如图所示为 $n = 4, m = 5$ 的情况）

容易维护每一步的行数上下界：上界 $U = i - m + 1$ 且 $U≥1U\ge 1$ ，下界 $D = i$ 且 $D≤nD\le n$ 。则第 $i$ 步的点有 ${(j,i−j+1)∣j∈[U,D]}\{(j,i-j+1)|j\in[U,D]\}$ 。

我们在这些点中找到字典序最小的作为第 $i$ 步的答案并转移。

但是最优点可能有很多个，因此我们计 $mark_{i,j}$ 表示点 $(i, j)$ 可以参与最小值计算。当点 $(j, i - j + 1)$ 的字母是最优点之一，就把 $(j + 1, i - j + 1)$ 和 $(j, i - j + 2)$ ，即右边和下面的点打上 $ma r k$ ，列入计算范围。

那么记得判断该点是否有 $ma r k$ 标记，再计算最小值。具体细节见代码：

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2002;
ll n,m;
char c[N][N],ans[N<<1];
bool mark[N][N];
int main()
{freopen("maze.in","r",stdin);  freopen("maze.out","w",stdout);scanf("%lld%lld",&n,&m);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)cin>>c[i][j];mark[1][1]=1;for(ll i=1;i<n+m;i++){ll U=max(1ll,i-m+1),D=min(n,i);char ret='z'+1;//	cout<<i<<":\n";for(int j=U;j<=D;j++){//	cout<<j<<" "<<i-j+1<<endl;if(mark[j][i-j+1]&&c[j][i-j+1]<ret)ret=c[j][i-j+1];}//	cout<<endl;cout<<ret;for(int j=U;j<=D;j++){if(mark[j][i-j+1]&&ret==c[j][i-j+1])mark[j][i-j+1+1]=mark[j+1][i-j+1]=1;else continue;}}return 0;
}

C.#3086 区域发展 / 洛谷 P5901 IOI 2009 Regions

题意

联合国区域发展委员任用了 $N$ 名委员，每名委员都属于及个地区中的一个。委员们按照其资历被编号为 $1$ 到 $N$ ， $1$ 号委员是主席，资历最高。委员所属地区被编号为 $1$ 到 $R$ 。除了主席之外所有委员都有一个直接导师。任何直接导师的资历都比他所指导的委员的资历要高。

我们说委员 A 是委员 B 的导师，当且仅当 A 是 B 的直接导师或者 A 是 B 的直接导师的导师。显然，主席是所有其他委员的导师，没有任何两名委员互为导师。

现在，联合国区域发展委员会想要建立一个计算机系统：在给定委员之间的直接导师关系的情况下，该系统可以自动地回答下述形式的问题：给定两个地区 $r 1$ 和 $r 2$ ，要求系统回答委员会中有多少对委员 $e 1$ 和 $e 2$ ，满足 $e 1$ 属于 $r 1$ ，且 $e 2$ 属于 $r 2$ ，并且 $e 1$ 是 $e 2$ 的导师。

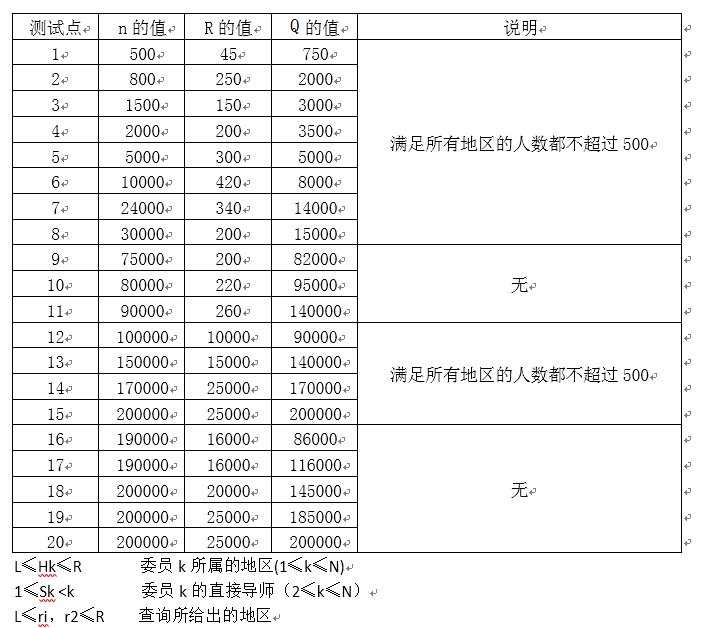
在这里插入图片描述
洛谷原题是交互题，强制在线。

思路

zc 说这是一道神题。这题的离线版本是蓝题。暴力做法是预处理每个城市之间的答案，然后每次 $O (1)$ 查询。

对询问离线并根据城市元素大小分块：如果 $r 2$ 个数不超过 $n\sqrt{n}$ ，那就可以遍历 $y$ 城市，向上找属于城市 $x$ 的导师；否则就不遍历 $y$ 转而遍历 $x$ ，向下找属于 $y$ 的委员。

（也就我要把这个离线根号分治讲那么冗杂了）

用两个 dfs 分别处理两部分的答案。对于向下找委员的，每次遍历到节点 $u$ 就更新所属城市 $a_u$ 的答案：令 $u$ 作为祖先，统计 $u$ 作为祖先时，有多少属于查询城市 $c$ 的委员在 $u$ 子树内，就向下 dfs 去统计。因为属于 $c$ 的总数更新了，于是记得先减去就的，等到遍历完 $u$ 子树回来之后再加上新的。

找祖先的话，遍历 $u$ 子树之前，直接先结算 $u$ 作为委员的贡献，统计 $a_u$ 个数 $+ 1$ ，遍历完再减 $1$ 。

具体细节见代码。

代码1

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2e5+9,R=2.5e4+9;
ll n,r,Q;
ll bSize;
ll a[N];
vector<ll>G[N],loc[R];
struct que
{ll c,id;
};
vector<que>r1[R],r2[R];
ll cnt[R],cnt2[R];
ll ans[N];
void dfs1(ll u,ll fa)//找子树 
{for(auto x:r1[a[u]])ans[x.id]-=cnt[x.c];for(auto v:G[u])dfs1(v,u);for(auto x:r1[a[u]])ans[x.id]+=cnt[x.c];cnt[a[u]]++;
}
void dfs2(ll u,ll fa)//找祖先 
{for(auto x:r2[a[u]])ans[x.id]+=cnt2[x.c];cnt2[a[u]]++;for(auto v:G[u])dfs2(v,u);cnt2[a[u]]--;
}
int main()
{freopen("regions.in","r",stdin);freopen("regions.out","w",stdout);scanf("%lld%lld%lld",&n,&r,&Q);bSize=sqrt(n);scanf("%lld",&a[1]);loc[a[1]].push_back(1);for(int i=2;i<=n;i++){ll fa;scanf("%lld%lld",&fa,&a[i]);loc[a[i]].push_back(i);G[fa].push_back(i);}for(int i=1;i<=Q;i++){ll x,y;scanf("%lld%lld",&x,&y);if(loc[y].size()<=bSize)r2[y].push_back((que){x,i});else r1[x].push_back({y,i});}dfs1(1,0);//枚举r1找r2 dfs2(1,0);//枚举r2找r1 for(int i=1;i<=Q;i++)printf("%lld\n",ans[i]);return 0;
}

在线的话也是根号分治。把城市成员个数大于 $n\sqrt {n}$ 的作为重城市，反之作为轻城市。预处理出重城市作为祖先或者委员查询的答案。如果两个都是轻城市，可以把判断城市是否为委员，转化为询问委员是否在祖先的 dfn 序的入端和出端之间。具体实现参考这篇博客。

D.#8028 数列 / 洛谷 P4108 HEOI2015 公约数数列

题意

设计一个数据结构. 给定一个正整数数列 $a0,a1,⋯,an−1a_0, a_1, \cdots, a_{n - 1}$ ，你需要支持以下两种操作：

$MODIFYidx\text{\texttt{MODIFY} \textit{id} \textit{x}}$ ：将 $a_{id}$ 修改为 $x$ ；
$QUERYx\text{\texttt{QUERY} \textit{x}}$ ：求最小的整数 $\ (0 \le p < n)$ ，使得 $gcd⁡(a0,a1,⋯,ap)×xor⁡(a0,a1,⋯,ap)=x\gcd(a_0, a_1, \cdots, a_p) \times \operatorname{xor}(a_0, a_1, \cdots, a_p) = x$ 。其中 $xor⁡(a0,a1,⋯,ap)\operatorname{xor}(a_0, a_1, \cdots, a_p)$ 代表 $a0,a1,⋯,apa_0, a_1, \cdots, a_p$ 的异或和， $gcd⁡\gcd$ 表示最大公约数。

$n≤105n\le10^5$ ， $q≤10000q\le 10000$ ， $1≤ai≤1091\le a_i\le 10^9$ ，询问操作中 $\le 10^{18}$ ，修改操作中 $0≤id<n0\le id<n$ ， $1≤x≤1091\le x\le 10^9$ 。

题意

看到这一题释怀了不少，在赛时最后 1h 选择了拼这题。写题解也感觉好写不少。

区间操作当然要用数据结构：离线用单调数据结构、线段树、树状数组、分块……

$gcd⁡\gcd$ 虽然单调不增但是不好在线段树上区间合并，而且这题是从头查到中间某点……

~~操作查询越奇怪，越要用分块！~~分块俗称最优美的暴力了，反正前几天正好 zc 讲了分块。

对 $a$ 序列分块，维护每一块的全部元素 $gcd⁡\gcd$ 和 $xor\mathrm{xor}$ 前缀和，分别记作 $bgc_i$ 和 $bsx_{i,j}$ 。

对于修改 $x$ 点数值，直接把 $x$ 所在块重构。查询的话从块 $1$ 到块 $cnt_b$ 扫过去。记 $G$ 和 $X$ 分别表示前缀 $gcd⁡\gcd$ 和 $xor\mathrm{xor}$ 之和。对于要加入的新块 $i$ ，有可能使 $G$ 改变也有可能不改变。

$bgc_i$ 能改变 $G$ 的，就在块 $i$ 扫 $bli∼bribl_i\sim br_i$ ，逐个更新 $G$ 和 $X$ ，这里是为了判断是否存在一个 $j$ 使得运算结果得到 $x$ 。

不能改变 $G$ 的，如果 $x$ 能整除 $G$ ，说明有可能在 $bli∼bribl_i\sim br_i$ 存在一个能得到结果 $x$ 的 $j$ ，同样逐个扫过去检验；否则直接跳过这个块， $X$ 异或上块 $i$ 异或和 $bsx_{i,m}$ 。

下表从 $0$ 开始，我代码是全部 $+ 1$ 然后答案 $- 1$ 。

代码1

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=1e5+9,B=319;
ll n,Q;
ll a[N];
ll bSize,cnt_b,bel[N],bl[B],br[B];
ll bsx[B][N],bgc[B];
void init()
{bSize=sqrt(n);cnt_b=n/bSize;if(n%bSize)cnt_b++;for(int i=1;i<=n;i++)bel[i]=(i-1)/bSize+1;for(int i=1;i<=cnt_b;i++){bl[i]=(i-1)*bSize+1;br[i]=i*bSize;}br[cnt_b]=n;for(int i=1;i<=cnt_b;i++){for(int j=bl[i];j<=br[i];j++){if(j==bl[i])bgc[i]=bsx[i][j]=a[j];else bgc[i]=__gcd(bgc[i],a[j]),bsx[i][j]=bsx[i][j-1]^a[j];}}
}
void modify(ll x,ll val)
{a[x]=val;ll xB=bel[x];bgc[xB]=0;for(int j=bl[xB];j<=br[xB];j++){if(j==bl[xB])bgc[xB]=bsx[xB][j]=a[j];else bgc[xB]=__gcd(bgc[xB],a[j]),bsx[xB][j]=bsx[xB][j-1]^a[j];}
}
ll query(ll x)
{ll Gcd=0,Xor=0;for(int i=1;i<=cnt_b;i++){if(Gcd==(Gcd==0?bgc[i]:__gcd(Gcd,bgc[i]))){if(x%Gcd==0){for(int j=bl[i];j<=br[i];j++)if(bsx[i][j]==((x/Gcd)^Xor))return j;}Xor^=bsx[i][br[i]];}else {for(int j=bl[i];j<=br[i];j++){Gcd=__gcd(Gcd,a[j]);Xor^=a[j];if(Gcd*Xor==x)return j; }}}return -1;
}
int main()
{
//	freopen("gcd.in","r",stdin);
//	freopen("gcd.out","w",stdout);scanf("%lld",&n);for(int i=1;i<=n;i++)scanf("%lld",&a[i]);init();scanf("%lld",&Q);while(Q--){string op;ll x,v;cin>>op;scanf("%lld",&x);if(op[0]=='M'){scanf("%lld",&v);modify(x+1,v);}else {ll ret=query(x);if(ret==-1)puts("no");else printf("%lld\n",ret-1);}}return 0;
}

其实在不会改变 $G$ 的部分，遍历找 $bsx_{i,j}$ 这一步可以用 map 优化到 $log⁡n\log n$ 。不过 map 常数太大了，赛时交带 map 的反挂到 60pts，暴力扫反而满分。

代码2

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=1e5+9,B=319;
ll n,Q;
ll a[N];
ll bSize,cnt_b,bel[N],bl[B],br[B];
ll bsx[B][N],bgc[B];
map<ll,ll>mp[B];
void init()
{bSize=sqrt(n);cnt_b=n/bSize;if(n%bSize)cnt_b++;for(int i=1;i<=n;i++)bel[i]=(i-1)/bSize+1;for(int i=1;i<=cnt_b;i++){bl[i]=(i-1)*bSize+1;br[i]=i*bSize;}br[cnt_b]=n;for(int i=1;i<=cnt_b;i++){for(int j=bl[i];j<=br[i];j++){if(j==bl[i])bgc[i]=bsx[i][j]=a[j];else bgc[i]=__gcd(bgc[i],a[j]),bsx[i][j]=bsx[i][j-1]^a[j];if(mp[i].find(bsx[i][j])==mp[i].end())mp[i][bsx[i][j]]=j;}}
}
void modify(ll x,ll val)
{a[x]=val;ll xB=bel[x];bgc[xB]=0;mp[xB].clear();for(int j=bl[xB];j<=br[xB];j++){if(j==bl[xB])bgc[xB]=bsx[xB][j]=a[j];else bgc[xB]=__gcd(bgc[xB],a[j]),bsx[xB][j]=bsx[xB][j-1]^a[j];if(mp[xB].find(bsx[xB][j])==mp[xB].end())mp[xB][bsx[xB][j]]=j;}
}
ll query(ll x)
{ll Gcd=0,Xor=0;for(int i=1;i<=cnt_b;i++){if(Gcd==(Gcd==0?bgc[i]:__gcd(Gcd,bgc[i]))){if(x%Gcd==0){//	for(int j=bl[i];j<=br[i];j++)//	if(bsx[i][j]==((x/Gcd)^Xor))return j;if(mp[i].find((x/Gcd)^Xor)!=mp[i].end())return mp[i][(x/Gcd)^Xor];}Xor^=bsx[i][br[i]];}else {for(int j=bl[i];j<=br[i];j++){Gcd=__gcd(Gcd,a[j]);Xor^=a[j];if(Gcd*Xor==x)return j; }}}return -1;
}
int main()
{freopen("gcd.in","r",stdin);freopen("gcd.out","w",stdout);scanf("%lld",&n);for(int i=1;i<=n;i++)scanf("%lld",&a[i]);init();scanf("%lld",&Q);while(Q--){string op;ll x,v;cin>>op;scanf("%lld",&x);if(op[0]=='M'){scanf("%lld",&v);modify(x+1,v);}else {ll ret=query(x);if(ret==-1)puts("no");else printf("%lld\n",ret-1);}}return 0;
}