P1983 [NOIP 2013 普及组] 车站分级
P1983 [NOIP 2013 普及组] 车站分级
题目背景
NOIP2013 普及组 T4
题目描述
一条单向的铁路线上,依次有编号为 1,2,…,n1, 2, …, n1,2,…,n 的 $n $ 个火车站。每个火车站都有一个级别,最低为 111 级。现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站 xxx,则始发站、终点站之间所有级别大于等于火车站 xxx 的都必须停靠。
注意:起始站和终点站自然也算作事先已知需要停靠的站点。
例如,下表是 $ 5 $ 趟车次的运行情况。其中,前 $ 4$ 趟车次均满足要求,而第 555 趟车次由于停靠了 333 号火车站(222 级)却未停靠途经的 666 号火车站(亦为 222 级)而不满足要求。
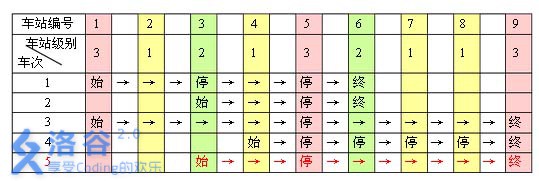
现有 mmm 趟车次的运行情况(全部满足要求),试推算这 $ n$ 个火车站至少分为几个不同的级别。
输入格式
第一行包含 222 个正整数 n,mn, mn,m,用一个空格隔开。
第 i+1i + 1i+1 行 (1≤i≤m)(1 ≤ i ≤ m)(1≤i≤m) 中,首先是一个正整数 si (2≤si≤n)s_i\ (2 ≤ s_i ≤ n)si (2≤si≤n),表示第 $ i$ 趟车次有 sis_isi 个停靠站;接下来有 $ s_i$ 个正整数,表示所有停靠站的编号,从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。
输出格式
一个正整数,即 nnn 个火车站最少划分的级别数。
输入输出样例 #1
输入 #1
9 2
4 1 3 5 6
3 3 5 6
输出 #1
2
输入输出样例 #2
输入 #2
9 3
4 1 3 5 6
3 3 5 6
3 1 5 9
输出 #2
3
说明/提示
对于 $ 20%$ 的数据,1≤n,m≤101 ≤ n, m ≤ 101≤n,m≤10;
对于 50%50\%50% 的数据,1≤n,m≤1001 ≤ n, m ≤ 1001≤n,m≤100;
对于 100%100\%100% 的数据,1≤n,m≤10001 ≤ n, m ≤ 10001≤n,m≤1000。
对于这题,我们可以将分级问题转化为拓扑问题。站点间按照车辆是否停靠来记录边关系。创建dp数组,dp[i] 表示从起点到站点 i 的路径长度,即最高等级。对于某一条线路上所有停靠了的站点和未停靠的站点,我们令未停靠的站点指向停靠了的站点,表示其等级高低。最后对于建好的图进行拓扑排序,并在排序过程中更新 dp[i] 。最后的答案为dp中的最大值。
建图时由于站点数量过多,可建立虚拟节点辅助建边。
#include<bits/stdc++.h>
using namespace std;int main(){ios_base::sync_with_stdio(false);cin.tie(NULL);int n, m;cin>>n>>m;vector<set<int>> g(n + m + 1);vector<int> in_(n + m + 1, 0);for (int i = 0; i < m; i++) {int dummy_ = n + 1 + i;int s;cin >> s;vector<int> stops(s);vector<bool> is_stopped(n + 1, false);for (int j = 0; j < s; j++) {cin >> stops[j];is_stopped[stops[j]] = true;}int start_ = stops.front();int end_ = stops.back();for (int u = start_; u <= end_; ++u) {if (!is_stopped[u]) {if(g[u].insert(dummy_).second) {in_[dummy_]++;}}}for (int v : stops) {if(g[dummy_].insert(v).second) {in_[v]++;}}}vector<int> dp(n + m + 1, 0);priority_queue<int, vector<int>, greater<>> pq;for(int i = 1; i <= n + m; i++){if(!in_[i]){pq.emplace(i);if (i <= n) {dp[i] = 1;}}}while(!pq.empty()){int v = pq.top();pq.pop();for(auto i : g[v]){in_[i]--;int is_path = (i <= n) ? 1 : 0;dp[i] = max(dp[i], dp[v] + is_path);if(!in_[i]){pq.emplace(i);}}}int ans = 0;for(int i = 1; i <= n; i++){ans = max(ans, dp[i]);}cout << ans;return 0;
}
