【动态规划 | 01背包】动态规划经典：01背包问题详解

算法	相关知识点	可以通过点击	以下链接进行学习	一起加油！
斐波那契数列模型	路径问题	多状态问题	子数组	子序列
回文字串

01背包是动态规划的经典问题，要求在容量限制下选择最大价值的物品。本文将详解如何通过状态转移方程高效求解，并给出空间优化方案，帮助掌握这一基础算法模型。

🌈个人主页：是店小二呀
🌈C/C++专栏：C语言\ C++
🌈初/高阶数据结构专栏： 初阶数据结构\ 高阶数据结构
🌈Linux专栏： Linux
🌈算法专栏：算法
🌈Mysql专栏:Mysql

🌈你可知:无人扶我青云志 我自踏雪至山巅

一·、背包问题

背包问题（Knapsack Problem） 是一种组合优化的 NP 完全问题，其核心目标是在限定的总重量内选择物品，使总价值最大化。

1.1 背包问题的分类

根据物品数量的限制，可分为以下几类：

• 0/1 背包问题：每种物品只能选一次。
• 完全背包问题：每种物品可选无限次。
• 多重背包问题：每种物品最多可选 s_i 次。
• 混合背包问题：物品的选取规则可能同时包含以上三种情况。
• 分组背包问题：物品被分为 n 组，每组最多选一个物品。

此外，背包问题还可根据 是否要求装满 背包分为：

1. 不一定装满背包。
2. 必须装满背包。

【优化方法】

1. 空间优化：滚动数组。
2. 单调队列优化。
3. 贪心优化（适用于特殊情况）。

1.2 背包问题的变种

根据 限定条件的个数，可进一步分类：

• 单约束背包（如仅受体积限制）→ 经典背包问题。
• 多重约束背包（如受体积和重量限制）→ 二维费用背包问题。

根据 不同的问法，还可以划分为：

• 输出具体方案。
• 求可行方案的总数。
• 寻找最优方案。
• 判断方案是否可行。

【总结】
背包问题的种类繁多，题型丰富，难度各异。但所有变种都源自 0/1 背包问题，因此掌握 0/1 背包 是学习背包问题的关键。

---

【模板】01背包

【题目】：【模板】01背包

【背包至多容量:算法思路】 (紫色字体为思路)

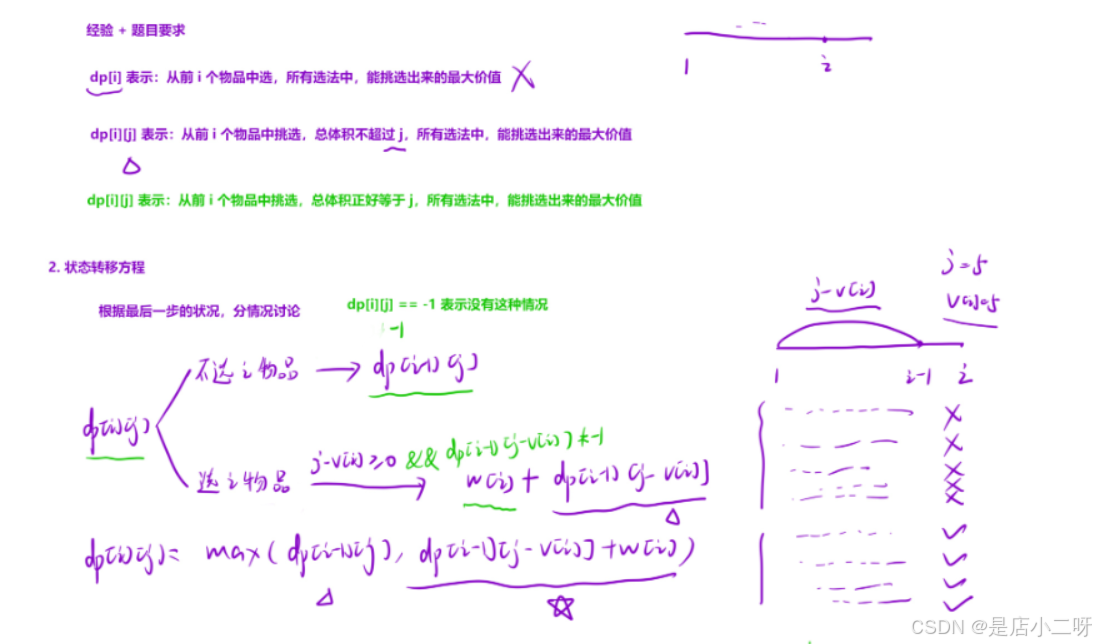
【状态表示】

对于物品个数为 1 的情况，存在选择和不选择两种决策方式。根据物品的属性和背包的容量要求进行约束，这即为 0-1 背包问题。

如果继续使用“从前 i 个物品中选择，所有选法中价值最大”来表示状态，这种方式无法清晰地描述状态，因为没有考虑背包容量的限制，因此无法推导出正确的状态转移方程。

因此，状态可以定义为：从 n 个物品中选择，且总容量不超过 j，求所有可行选择方案中的最大价值。

【状态转移方程】

在进行线性 DP 状态转移方程分析时，一般根据“最后一步”的情况进行分情况讨论：

1. 不选第 i 个物品：此时问题就转化为从前 i-1 个物品中选择，总体积不超过 j。因此，状态转移方程为：
   dp[i][j] = dp[i−1][j]

2. 选择第 i 个物品：此时我们只能从前 i-1 个物品中选择，总体积不超过 j−v[i]。此时的状态转移方程为：dp[i][j] = dp[i - 1][j - v[i]] + w[i] 。但是这种状态不⼀定存在，因此需要特判⼀下

   综上，状态转移⽅程为： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i])

【初始化】

我们可以额外添加一行，以方便初始化。此时，只需将第一行初始化为 0，因为在不选择任何物品的情况下，能够满足背包容量不小于 j 的条件，其对应的价值为 0

【代码实现】

#include <iostream>
#include<string.h>
using namespace std;const int N = 1010;
int n, V, v[N], W[N];
int dp[N][N];int main()
{cin >> n >> V;for(int i = 1; i <= n; i++) cin >> v[i] >> W[i];//解决第一问for(int i = 1; i <= n; i++){for(int j = 0; j <= V; j++){dp[i][j] = dp[i - 1][j];if(j >= v[i])dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + W[i]);}}cout << dp[n][V] << endl;

【细节问题】

牛客网属于ACM模式需要整体实现，对此一般定义全局变量，默认数值尾0，无需特殊的初始化。

【背包恰好装满:算法思路】 (绿色字体为思路)

在第二问中，仅需对 DP 过程的五个步骤进行微调。由于可能无法凑齐体积为 j 的物品，因此将不合法的状态设为 -1。格子元素初始化为 0，表示体积为 0 的背包。

对于第一行，除了第一个格子外，其余格子均设为 -1，表示在没有物品的情况下，无法满足体积大于 0 的条件。没有这种情况就算了，表示当前也不符合状态表示。

可以细看两个状态表示，可以更加理解算法思路。

2.状态转移方程

需要考虑无法满足需求的情况。对于不选第 i 个物品的情况，不需要额外判断，因为如果之前没有选择，就不可能现在选择。对于选择第 i 个物品的情况，需要判断：首先，容量是否足够，即j >=v[j]。

其次，前一状态 dp[i−1][j−v[i]] 是否有效，以确保可以选择第 i 个物品。此外，还需考虑 w[i]数值过大会影响结果。

【初始化】

我们需要添加额外的初始化步骤：

1. 第一个格子初始化为 0，因为体积为 0 的背包可以正好不选任何物品，满足要求。
2. 但是，第一行后面的格子都初始化为 -1，表示没有物品的情况下，无法满足体积大于 0 的需求。

【代码实现】

    //解决第二问memset(dp, 0, sizeof dp);for(int j = 1; j <= V; j++) dp[0][j] = -1;for(int i = 1; i <= n; i++){for(int j = 0; j <= V; j++){dp[i][j] = dp[i - 1][j];if(j >= v[i] && dp[i - 1][j - v[i]] != -1)dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + W[i]);}}cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl;return 0;
}

【优化方案】

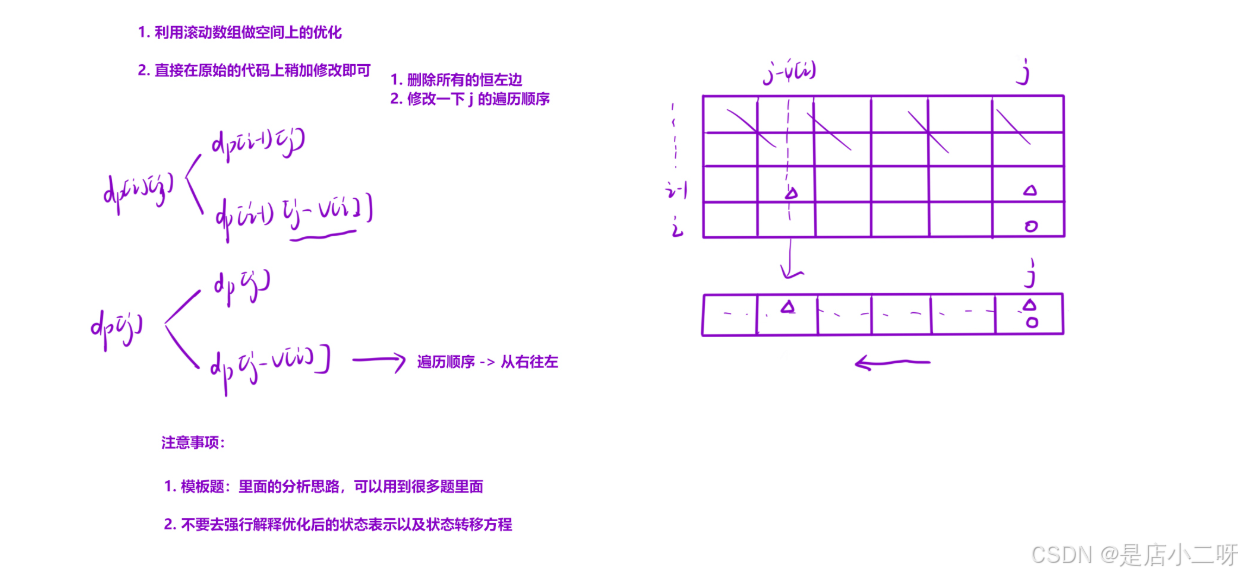
状态表示为从前 i 个物品中挑选，满足背包容量不超过 j 的条件，得到的最大价值。每次 i++ 时，通过转移状态来更新当前的最优解，因此可以通过状态转移方程来解决此类问题。

为了优化空间复杂度，我们使用滚动数组技巧，将二维数组压缩为一维。这样，我们可以删除所有的横坐标，只保留纵坐标。同时，修改 j 的遍历顺序，逆序遍历 j，避免在更新状态时覆盖尚未处理的数据。

#include <iostream>
#include<string.h>
using namespace std;const int N = 1010;
int n, V, v[N], W[N];
int dp[N];int main()
{cin >> n >> V;for(int i = 1; i <= n; i++) cin >> v[i] >> W[i];//解决第一问for(int i = 1; i <= n; i++){for(int j = V; j >= v[i] ; j--){dp[j] = max(dp[j], dp[j - v[i]] + W[i]);}}cout << dp[V] << endl;//解决第二问memset(dp, 0, sizeof dp);for(int j = 1; j <= V; j++) dp[j] = -1;for(int i = 1; i <= n; i++){for(int j = V; j >= v[i] ; j--){if(dp[j - v[i]] != -1)dp[j] = max(dp[j], dp[j - v[i]] + W[i]);}}cout << (dp[V] == -1 ? 0 : dp[V]) << endl;return 0;
}

---

461.分割等和子集

【题目】：416. 分割等和子集

【算法思路】

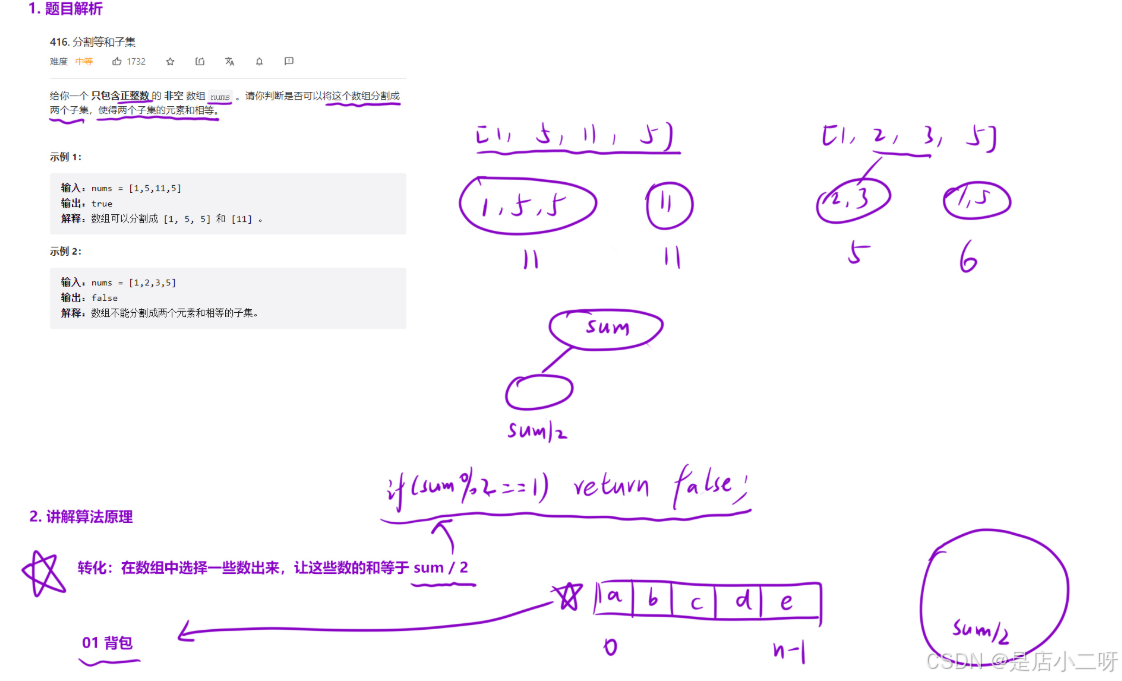
根据题目要求和模拟过程，从中发现"算法思路"。对此，我们可以发现，如果sum是偶数，存在真的情况，但是sum为奇数，不存在这类情况。sum是一个值，sum/2是判断是否为真的目标。

对此将sum / 2当作背包的容量，对于数组元素当作选取物品是进行选择，同时存在物品体积或者价格，就是本身的数值。

根据最后一个位置考虑，得到状态转移方程。

【代码实现】

class Solution {
public:bool canPartition(vector<int>& nums) {int n = nums.size(), sum = 0;for(auto x : nums) sum += x;int aim = sum / 2;if(sum % 2) return false;vector<vector<bool>> dp(n + 1, vector<bool>(aim + 1));for(int i = 0; i <= n; i++) dp[i][0] = true;for(int i = 1; i <= n; i++){for(int j = 1; j <= aim; j++){dp[i][j] = dp[i - 1][j];if(j >= nums[i - 1]) dp[i][j] = dp[i][j] || dp[i - 1][j -nums[i - 1]];}}return dp[n][aim];}
};

【优化方案】

通过使用滚动数组技巧，我们可以删除二维数组中的行，将其压缩为一维数组，从而节省空间。在状态转移时，修改 j 的遍历顺序，采用逆序遍历 j，避免覆盖尚未处理的状态。这种优化不仅减少了空间复杂度，也确保了数据的正确性。

class Solution {
public:bool canPartition(vector<int>& nums) {int n = nums.size(), sum = 0;for(auto x : nums) sum += x;int aim = sum / 2;if(sum % 2) return false;vector<bool> dp(aim + 1);dp[0] = true;for(int i = 1; i <= n; i++){for(int j = aim; j >= nums[i - 1]; j--){dp[j] = dp[j] || dp[j -nums[i - 1]];}}return dp[aim];}
};

---

494. 目标和

【题目】：494. 目标和

【算法思路】

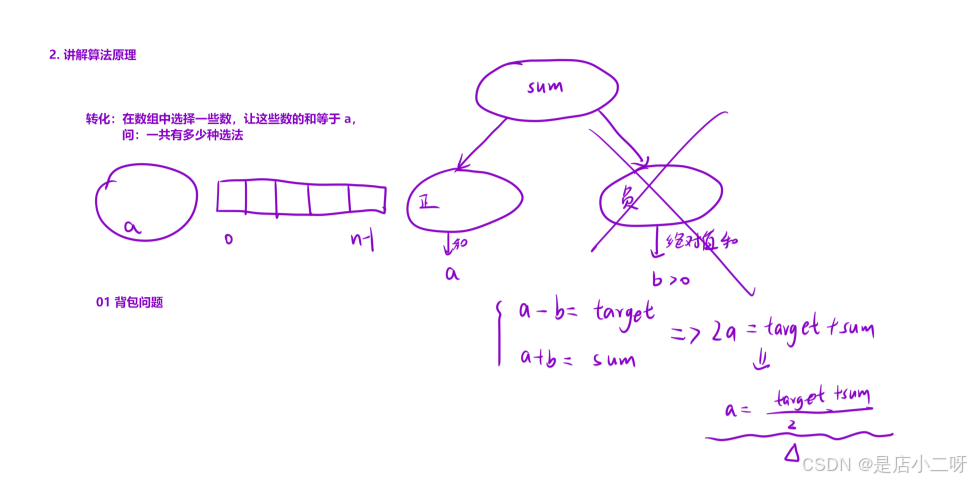
据题目要求和模拟过程，提炼出算法思路。首先，计算数组元素的总和，并将其划分为正负两部分。通过数学分析，将两个表达式相加并消除未知数，从中得出关键目标 amid = target + sum / 2。接着，将 amid 视为背包的容量，数组元素作为选取的物品，物品的体积或价值即为其对应的数值。

这里需要注意的是，问的是总共有多少种选法，因此不需要加 1。在原有基础上添加一个元素并不会增加新的选法，而只是多了一种选择方式。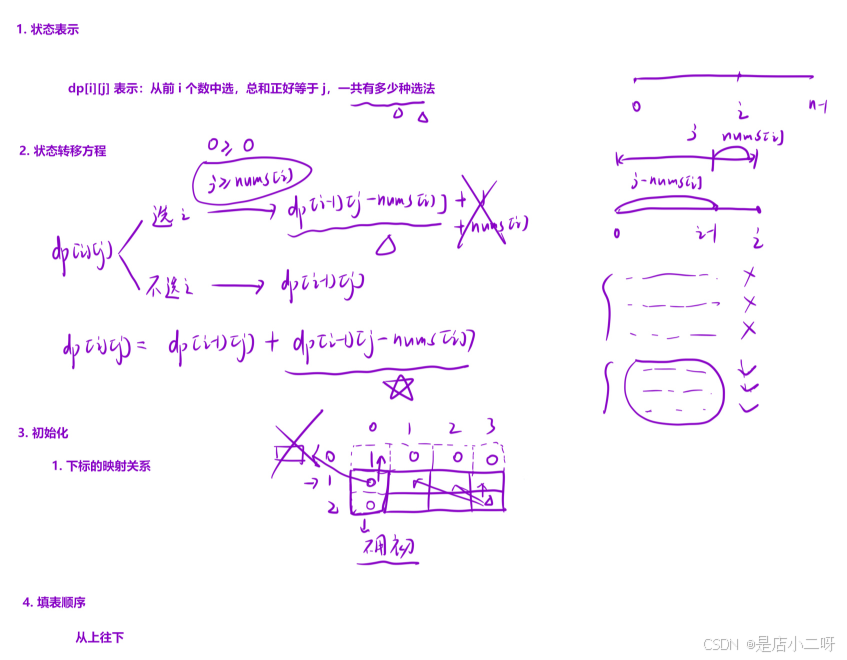

【初始化】

这里只需初始化第一行。在循环中完成第一类的初始化，并且不会发生越界问题，因为 j >= nums[i] 时会使用 i-1 位置的元素，而不会访问右侧越界的数据。

【代码实现】

class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int n = nums.size();int sum = 0;for(auto x: nums) sum += x;int aim = (target + sum) / 2;if(aim < 0 || (target + sum) % 2) return 0;//1.创建dp表vector<vector<int>> dp(n + 1, vector<int>(aim + 1));dp[0][0] = 1;//2.填表for(int i = 1; i <= n; i++){for(int j = 0; j <= aim; j++){dp[i][j] = dp[i - 1][j];if(j >= nums[i - 1])dp[i][j] += dp[i - 1][j - nums[i - 1]];}}  //3.返回值处理return dp[n][aim];}
};

【优化方案】

所有的背包问题都可以进行空间优化。对于 01 背包问题，优化策略是：去掉第一维，并修改第二层循环的遍历顺序。

class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int n = nums.size();int sum = 0;for(auto x: nums) sum += x;int aim = (target + sum) / 2;if(aim < 0 || (target + sum) % 2) return 0;//1.创建dp表vector<int> dp(aim + 1);dp[0] = 1;//2.填表for(int i = 1; i <= n; i++){for(int j = aim; j >= nums[i - 1]; j--){dp[j] += dp[j - nums[i - 1]];}}  //3.返回值处理return dp[aim];}
};

---

1049. 最后一块石头的重量 II

【题目】：1049. 最后一块石头的重量 II

【算法思路】

根据题目要求和模拟过程，提炼出算法思路。首先，计算数组元素的总和，并根据题意将其划分为正负两部分。目标是找到 |a - b| 的最小值，同时满足 a + b = sum，从而得到关键目标值。

需要注意的是，题目并未明确给出所需数值，而是要求‘石头最小的可能重量’。因此，我们将问题转化为：在数组中选择一些数，使得它们的和尽可能接近 sum / 2。

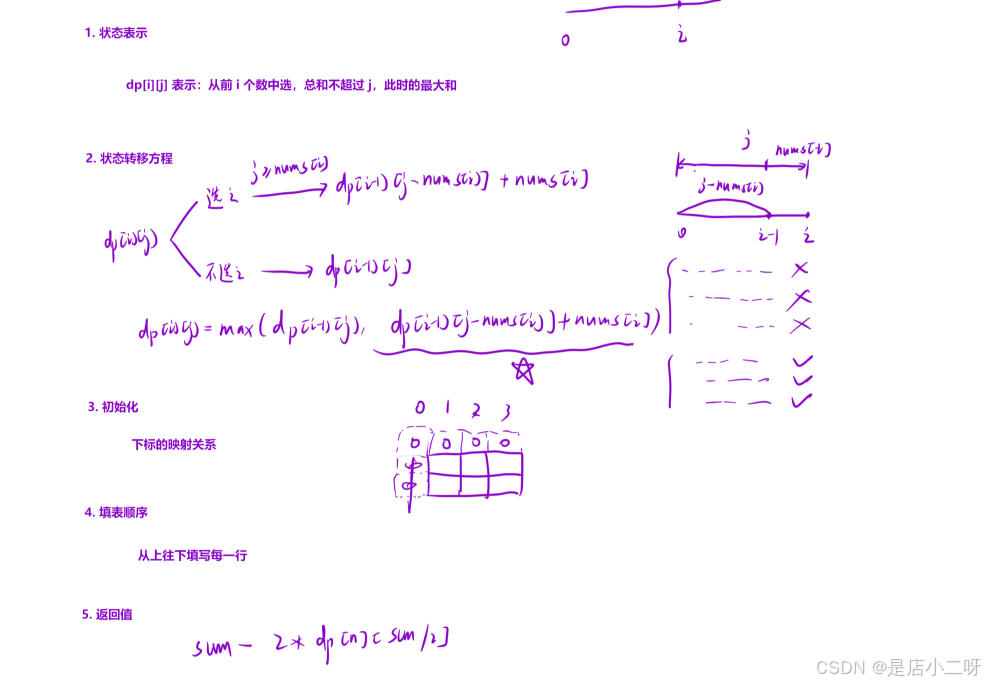
【初始化】

这里只需初始化第一行。在循环中完成第一类的初始化，并且不会发生越界问题，因为 j >= nums[i] 时会使用 i-1 位置的元素，而不会访问右侧越界的数据。

【代码实现】

class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum = 0;for(auto x : stones) sum += x;int amid = sum / 2;//1.创建dp表int n = stones.size();vector<vector<int>> dp(n + 1, vector<int>(amid + 1));//2.填表操作for(int i = 1; i <= n; i++){for(int j = 0; j <= amid; j++){dp[i][j] = dp[i - 1][j];if(j >= stones[i - 1])dp[i][j] = max(dp[i][j], dp[i - 1][j - stones[i - 1]] + stones[i - 1]);}}//3.返回值处理return sum - 2 * dp[n][amid];}
};

【优化方案】

class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum = 0;for(auto x : stones) sum += x;int amid = sum / 2;//1.创建dp表int n = stones.size();vector<int> dp(amid + 1);//2.填表操作for(int i = 1; i <= n; i++){for(int j = amid; j >= stones[i - 1]; j--){dp[j] = max(dp[j], dp[j - stones[i - 1]] + stones[i - 1]);}}//3.返回值处理return sum - 2 * dp[amid];}
};

快和小二一起踏上精彩的算法之旅！关注我，我们将一起破解算法奥秘，探索更多实用且有趣的知识，开启属于你的编程冒险！