初识opencv02——图像预处理1

初识opencv

初识opencv01——基本api操作

---

---

一、图像变换

1.1 图像翻转

图像翻转是图像处理中基础但重要的操作，OpenCV通过cv2.flip()函数实现镜像翻转，常用于数据增强或图像对称性分析。

这里给出一份示例代码：

import cv2 as cvimg = cv.imread("cat.jpg")
# 水平翻转（左右镜像）
horizontal_flip = cv.flip(img, 1)  
# 垂直翻转（上下翻转）
vertical_flip = cv.flip(img, 0)    
# 同时水平和垂直翻转
both_flip = cv.flip(img, -1)      cv.imshow("Original", img)
cv.imshow("Horizontal Flip", horizontal_flip)
cv.imshow("Vertical Flip", vertical_flip)
cv.waitKey(0)

其中所使用的api为：

• cv2.flip(img,flipcode)
  在OpenCV中，图片的镜像旋转是以图像的中心为原点进行镜像翻转的。参数img为要翻转的图像，flipcode为指定翻转类型的标志。

• flipcode=0: 垂直翻转，图片像素点沿x轴翻转
• flipcode>0: 水平翻转，图片像素点沿y轴翻转
• flipcode<0: 水平垂直翻转,水平翻转和垂直翻转的结合

1.2 仿射变换

仿射变换（Affine Transformation）是一种线性变换,保持了点之间的相对距离不变，具体来说就是变换后直线仍旧是直线，平行线依旧是平行线，线段间比例不变。

在opencv中仿射变换所使用的api为cv2.warpAffine()函数，用法如下：

cv2.warpAffine(img,M,dsize)

• img：输入图像。
• M：2x3的变换矩阵，类型为np.float32。
• dsize：输出图像的尺寸，形式为(width,height)。

• 变换矩阵
  在二维空间中，图像点坐标为$(x,y)$，仿射变换的目标是将这些点映射到新的位置$(x^{\prime },y^{\prime })$，仿射变换是一种线性变换，类似于$x^{\prime }=kx+b$。为了实现这种映射，通常会使用一个矩阵乘法的形式：

$$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{l}abtx\\ cdty\\ 001\end{array}\right]\ast \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$

其中$\left[\begin{array}{l}abtx\\ cdty\\ 001\end{array}\right]$即为变换矩阵，其第三行并不参与变换，去掉后$\left[\begin{array}{l}abtx\\ cdty\end{array}\right]$，即可作为函数cv2.warpAffine(img,M,dsize)的参数使用

• 齐次坐标
  将$\left[\begin{array}{c}x\\ y\end{array}\right]$扩展为$\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$，这种扩展后的坐标称之为齐次坐标。这种形式能够同时统一旋转、平移、缩放、剪切这四种变换。

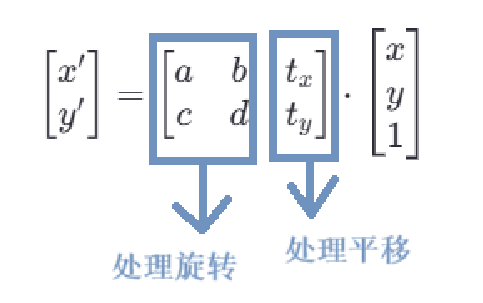
既然变换矩阵的第三行不参与变换，那为什么还需要写成这种形式呢？

而将$\left[\begin{array}{l}abtx\\ cdty\end{array}\right]$扩展为$\left[\begin{array}{l}abtx\\ cdty\\ 001\end{array}\right]$，能够使原来的2*3矩阵变为方阵，这样就可以可求解矩阵的逆，也即是该变换的逆变换。

常见仿射变换有以下几种：

1.2.1 图像旋转

在计算机中所有图像都由像素点组成，故在此先探究单个点绕中心旋转的情况。
令旋转中心为坐标系中心O（0，0），假设有一点$P_0(x_0,y_0)$，$P_0$离旋转中心O的距离为r，$O{P}_0$与坐标轴x轴的夹角为$\alpha$，$P_0$绕O顺时针旋转$\theta$角后对应的点为$P(x,y)$。

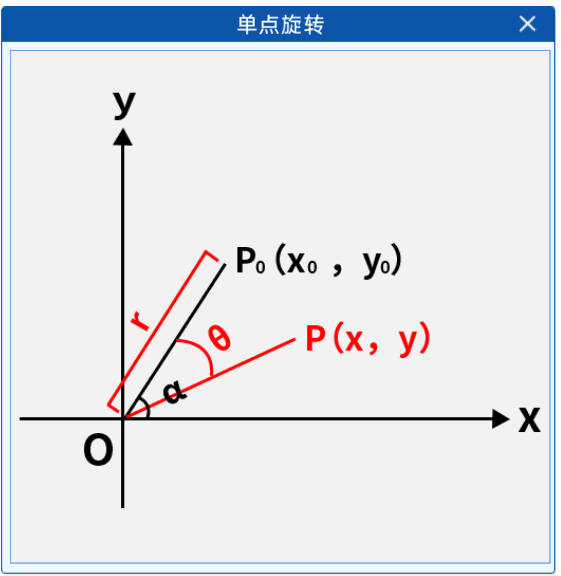
以极坐标形式表示坐标可得：

$x_0=r\times \cos \alpha$，$y_0=r\times \sin \alpha$

$x=r\times \cos (\alpha -\theta )=r\cos \alpha \cos \theta +r\sin \alpha \sin \theta =x_0\cos \theta +y_0\sin \theta$
$y=r\times \sin (\alpha -\theta )=r\sin \alpha \cos \theta -r\cos \alpha \sin \theta =-x_0\sin \theta +y_0\cos \theta$

用矩阵来表示就是:
$$\left[\begin{array}{l}x\\ y\end{array}\right]=\left[\begin{array}{l}\cos \theta \sin \theta \\ -\sin \theta \cos \theta \end{array}\right]\ast \left[\begin{array}{c}{x}_0\\ y_0\end{array}\right]$$
然而，在OpenCV中，旋转时是以图像的左上角为旋转中心，且以逆时针为正方向，因此上面的例子中其实是个负值，那么该矩阵可写为：
$$\left[\begin{array}{l}x\\ y\end{array}\right]=\left[\begin{array}{l}\cos \theta -\sin \theta \\ \sin \theta \cos \theta \end{array}\right]\ast \left[\begin{array}{c}{x}_0\\ y_0\end{array}\right]$$
若需要围绕任意点进行旋转。那么我们可以将其转化成绕原点的旋转，其过程为：

1. 首先将旋转点移到原点
2. 按照上面的旋转矩阵进行旋转得到新的坐标点
3. 再将得到的旋转点移回原来的位置

1.2.2 图像平移

平移操作即是将图像中的每个点沿着某个方向移动一定的距离。假设我们有一个点 $P(x,y)$，希望将其沿x轴方向平移$t_x$个单位，沿y轴方向平移$t_y$个单位到新的位置$P\prime (x\prime ,y\prime )$，那么平移公式如下：
​$$x\prime =x+tx，y\prime =y+ty$$
在矩阵形式下，该变换可以表示为：
$$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{l}10tx\\ 01ty\end{array}\right]\ast \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$
这里的$t_x$和$t_y$分别代表在x轴和y轴上的平移量。

1.2.3 图像缩放

缩放操作可以改变图片的大小。设图像的宽高所对应的缩放因子分别为sx，sy则
点$P(x,y)$对应到新的位置$P^{\prime }(x^{\prime },y^{\prime })$，缩放公式为：

$$x\prime =s_x\ast x，y\prime =s_y\ast y$$
在矩阵形式下，该变换可以表示为：
$$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{l}sx00\\ 0sy0\end{array}\right]\ast \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$

1.2.4 图像剪切

剪切操作可以改变图形的形状，以便其在某个方向上倾斜，它将对象的形状改变为斜边平行四边形，而不改变其面积。
对于二维空间中的点$P(x,y)$，对他进行剪切变换：

沿x轴剪切：$x^{\prime }=x+s{h}_y\ast y$

沿y轴剪切：$y^{\prime }=s{h}_x\ast x+y$

在矩阵形式下，该变换可以表示为：
$$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{l}1sh0\\ sh10\end{array}\right]\ast \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$

1.3 图像叠加

可以使用OpenCV的cv.add()函数把两幅图像相加，或者可以简单地通过numpy操作添加两个图像，如res = img1 + img2。两个图像应该具有相同的大小和类型。
**OpenCV加法和Numpy加法之间存在差异。OpenCV的加法是饱和操作，而Numpy添加是模运算。**
示例：OpenCV加法

import cv2 as cvimg1 = cv.imread("background.jpg")
img2 = cv.imread("overlay.jpg")# 确保两图尺寸一致
assert img1.shape == img2.shape, "图像尺寸需相同"# OpenCV加法（饱和操作）
result = cv.add(img1, img2)cv.imshow("OpenCV Add", result)
cv.waitKey(0)

也可使用**cv2.addWeighted(src1,alpha,src2,deta,gamma)**对图片进行加权叠加。
示例：Numpy加法

# Numpy加法（模运算）
result_np = img1 + img2cv.imshow("Numpy Add", result_np)
cv.waitKey(0)

二、图像色彩空间

2.1 RGB

RGB（Red, Green, Blue）是最常见的色彩空间，通过红、绿、蓝三原色通道的线性叠加表示颜色。在OpenCV中，图像默认以BGR格式存储（通道顺序不同），需注意与标准RGB的差异。

2.2 HSV

HSV（Hue, Saturation, Value）色彩空间将颜色信息（色相H）、纯度（饱和度S）与亮度（明度V）分离，更适合颜色识别与分割。

三、灰度化

3.1 灰度图

灰度图（Grayscale Image）是每个像素仅表示亮度信息的单通道图像，像素值范围通常为0（黑）到255（白）。与彩色图像相比，灰度图丢失了颜色信息，但保留了亮度结构。

灰度图常用于以下场景：

• 图像预处理 ：边缘检测、轮廓提取的前置步骤（如Canny算子）。
• 特征提取 ：减少计算量，提升文本识别、模板匹配效率。
• 医学成像 ：CT/MRI图像的亮度直接反映组织密度。

这里给出一个获取灰度图像的示例代码：

import cv2 as cv# 读取彩色图像
img = cv.imread("color_image.jpg")  
# 将BGR图像转换为灰度图
gray_img = cv.cvtColor(img, cv2.COLOR_BGR2GRAY)  cv.imshow("Original", img)
cv.imshow("Grayscale", gray_img)
cv.waitKey(0)

3.2 灰度化的常用方法

灰度化本质是将三通道彩色值映射为单通道灰度值，常见方法包括平均法、加权平均法 和OpenCV内置函数 。

• 最大值法
  取R、G、B三通道中的最大值：
  $$Gray=Max(R，G，B)$$

• 平均法
  对R、G、B三通道取算术平均值：
  $$Gray=\frac{R+G+B}{3}$$

• 加权平均法
  根据人眼对不同颜色的敏感度分配权重（如NTSC标准）：
  $$Gray=0.299R+0.587G+0.114B$$

• OpenCV内置函数
  cv2.cvtColor()内部优化了颜色空间转换效率，推荐用于实际项目：

gray_cv = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
cv.imshow("OpenCV Grayscale", gray_cv)

四、二值化

4.1 二值图像

二值图像是指每个像素仅取两个值（通常为0和255）的图像，常用于图像分割、目标检测 等场景。通过二值化可将复杂图像简化为黑白两部分，突出目标与背景的边界。与灰度图一样，二值图为单通道图像，仅保留目标与背景的区分，丢失细节信息。

4.2 阈值化与反阈值化

• 阈值法
  就是通过设置一个阈值，将灰度图中的每一个像素值与该阈值进行比较，小于等于阈值的像素就被设置为0（通常代表背景），大于阈值的像素就被设置为maxval（通常代表前景）。对于我们的8位图像(0~255)来说，通常是设置为255。

• 反阈值化
  顾名思义，就是与阈值法相反。反阈值法是当灰度图的像素值大于阈值时，该像素值将会变成0（黑），当灰度图的像素值小于等于阈值时，该像素值将会变成maxval。

这里给出一个对比阈值化与反阈值化图像的示例代码：

import cv2 as cvgray_img = cv.imread("logo.jpg", 0)  
# 阈值化
_, binary = cv.threshold(gray_img, 127, 255, cv.THRESH_BINARY)  
# 反阈值化
_, binary_inv = cv.threshold(gray_img, 127, 255, cv.THRESH_BINARY_INV)  cv.imshow("Original", gray_img)
cv.imshow("Binary", binary)
cv.imshow("Binary Inverse", binary_inv)
cv.waitKey(0)

4.3 超阈值零处理与低阈值零处理

• 超阈值零处理
  就是将灰度图中的每个像素与阈值进行比较，像素值大于阈值的部分置为0（也就是黑色），像素值小于等于阈值的部分不变。

示例：

import cv2 as cv# 读取过曝图像
img = cv.imread("overexposed.jpg", 0)  
# 设置阈值127，超阈值零处理
_, result = cv.threshold(img, 127, 255, cv.THRESH_TOZERO_INV)  cv.imshow("Original", img)
cv.imshow("Threshold TOZERO_INV", result)
cv.waitKey(0)

• 低阈值零处理
  字面意思，就是像素值小于等于阈值的部分被置为0（也就是黑色），大于阈值的部分不变。
  示例：

import cv2 as cv# 读取暗背景图像
img = cv.imread("dark_background.jpg", 0)  
# 设置阈值127，低阈值零处理
_, result = cv.threshold(img, 127, 255, cv2.THRESH_TOZERO)  cv.imshow("Original", img)
cv.imshow("Threshold TOZERO", result)
cv.waitKey(0)

4.4 截断阈值法

截断阈值法，指将灰度图中的所有像素与阈值进行比较，像素值大于阈值的部分将会被修改为阈值，小于等于阈值的部分不变。换句话说，经过截断阈值法处理过的二值化图中的最大像素值就是阈值。

4.5 OSTU阈值法

也称大津法，是一种自动获取最佳阈值的方法。THRESH_OTSU 本身并不是一个独立的阈值化方法，而是与 OpenCV 中的二值化方法结合使用的一个标志，默认情况下它会与 THRESH_BINARY 结合使用。

OTSU阈值法适用于双峰图片，双峰图片就是指灰度图的直方图上有两个峰值，直方图就是对灰度图中每个像素值的点的个数的统计图，如下图所示。

使用OTSU算法计算阈值时，组件中的thresh参数将不再有任何作用。

4.6 自适应阈值法

自适应阈值法（Adaptive Thresholding）通过为图像的每个局部区域动态计算阈值，解决光照不均 或复杂背景 下的图像分割问题。与全局阈值法（如OSTU）不同，它能适应不同区域的亮度变化，常用于文档扫描、手写识别 等场景。

• 取均值（ADAPTIVE_THRESH_MEAN_C）
  阈值 T(x,y) 为局部区域像素的平均值减去常数 C ，适用于光照变化较均匀 的场景。

这里给出一个均值自适应阈值的示例代码：

import cv2 as cv# 读取灰度图像（如扫描文档）
gray_img = cv.imread("uneven_lighting_doc.jpg", 0)  
# 均值自适应阈值（局部区域11x11，常数C=2）
binary_mean = cv.adaptiveThreshold(gray_img, 255, cv.ADAPTIVE_THRESH_MEAN_C, cv.THRESH_BINARY, blockSize=11, C=2)  cv.imshow("Mean Adaptive Binary", binary_mean)
cv.waitKey(0)

• 加权求和（ADAPTIVE_THRESH_GAUSSIAN_C）
  阈值 T(x,y) 为局部区域像素的高斯加权和减去常数 C ，权重由像素距离中心点的远近决定（距离越近权重越高）。

这里给出一个高斯加权自适应阈值的示例代码：

# 高斯加权自适应阈值（局部区域11x11，常数C=2）
binary_gaussian = cv2.adaptiveThreshold(gray_img, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY, blockSize=11, C=2)  cv2.imshow("Gaussian Adaptive Binary", binary_gaussian)
cv2.waitKey(0)

---

总结

本文介绍了OpenCV图像预处理的五大基础操作，这些方法是后续图像分析的重要基础。实际应用中可根据需求组合使用，并调整参数以获得最佳效果。