【计算机三级网络】——选择题高频考点(第一篇)

ℹ️大家好，我是练小杰，不知不觉7月份就要过去了，暑假都去哪里玩耍了呀！！
欢迎来到9月份的三级网络技术考试的选择题知识篇，感谢大佬们的支持😆

在这里，也大力感谢B站up主“名副其实举世无双” 和 “吃饭不留名” 的无私分享🌹🌹

---

计算机证书专栏：🔝 【二级C语言】【三级网络技术】

---

计算机三级网络大题合集：🔝

1. 【 IP地址大题(第一道)：计算网络号，广播地址，主机号，可用地址，子网掩码等】

2. 【IP校园网大题(第二道)：路由代码填空】

3. 【DHCP报文分析(第三道大题)】

4. 【Sniffer抓包 和Wireshark 抓包(第四道大题)】

5. 【应用题：聚合IP地址和划分子网】

---

数据库专栏：👉【数据库专栏】【Mysql练习题】

主页：👉【练小杰的CSDN】

‌"幸福属于满足的人们~~"‌

前言

通过前面的几篇博客，我们已经总结了大题的答题模版以及套路。接下来，将要解决选择题的高频考点！！！gogogo！！！

考点精讲

IPV6判断正误

IPV6地址有8个段位，每个段位有 16 个二进制位，一共128位二进制数。
例如：615A:0000:0000:02EA:000F:FEOC:9C5B

前导零压缩方法

经过前导零压缩后，把段位中全0的变为1个0，且把每个段位中开头为0的省略！！！

前导零压缩：
615A:0:0:0:2EA:F:FEOC:9C5B 

双冒号压缩法(省略连续段位的0)

⚠️注意：双冒号只能出现一次，且8个段位不多不少！！

省略连续段位的零后，只留一个双冒号，在后面出现任何一个双冒号都是错误❎

双冒号压缩法: 	
615A::02EA:000F:FEOC:9C5B

同时用两种方法

两种都用：
615A::2EA:F:FE0C:9C5B

真题实训

题目1：判断给出的IPv6地址简化正误

IPV6地址FE80:0:0:0801:FE:0:0:04A1
已知，在每个段位中，前导0可以省略；且有连续段位的零也能省略。

题目A选项中，FE80 变为 FE8，这个0是有效的，不能省略!!!

• 答案：
  

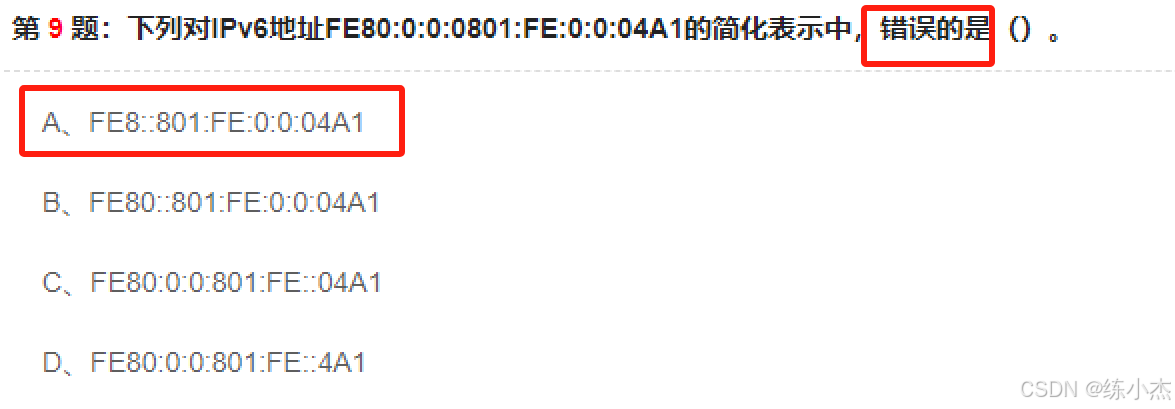
题目2：在四个选项中判断正误

题目可知，C选择中出现两个双冒号，错误❎

停机时长与系统可用性

可用性	停机时间 (年)
99.9	<= 8.8 小时
99.99	<= 53分钟
99.999	<= 5分钟

真题1

• 本题答案为A，问可用性 99.999% 的每年停机时间
  

真题2

考察两台服务器的停机时间之和 以及 停机时间之差

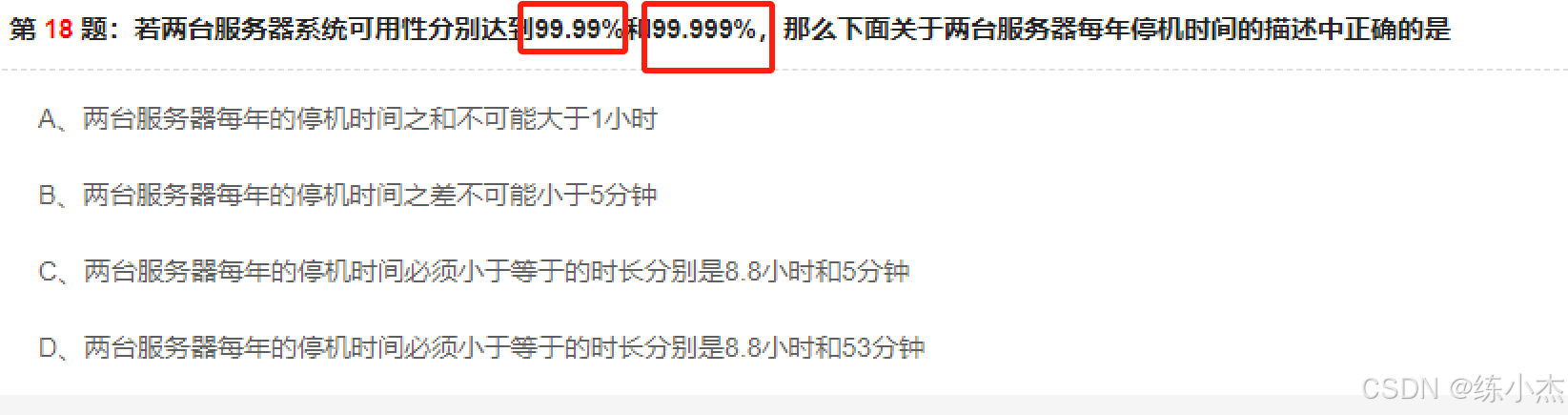
99.99 对应停机时间 <=53分钟
99.999 对应停机 <=5分钟
两台每年停机时间之和(最大)： <=58分钟

答案：

三种备份比较

记住下列表格的比较即可，主要看最大和最小的！！！

比较	最大(最快)		最小(最慢)
空间使用	完全备份	差异备份	增量备份
备份速度	增量备份	差异备份	完全备份
恢复速度	完全备份	差异备份	增量备份

真题练习1

题目问的是恢复速度由慢到快，通过上面表格分析恢复速度由快到慢为 完全>差异>增量，即题目答案为 增量<差异< 完全 (与表格相反)
答案为：

真题练习2

通过题目选项可看到，B选项中的差异备份是比增量备份的恢复快的，即恢复速度由快到慢为： 完全>差异> 增量
答案为：B选项错误

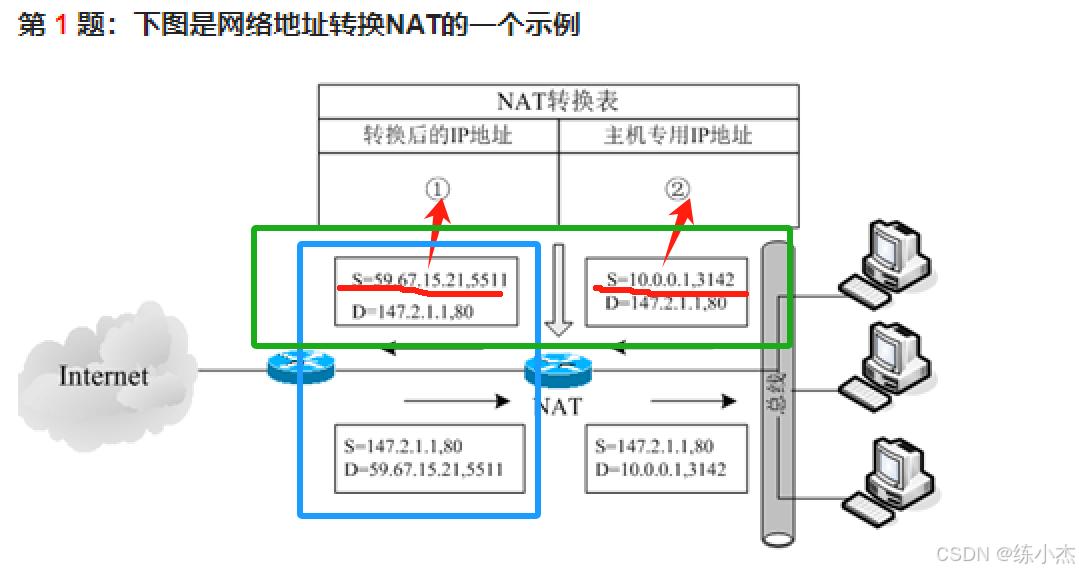
网络地址转NAT

1. NAT转换表中的IP地址(即①和②)，分别对应绿色框的两个源地址(S)， 且绿色框内的 目的地址(D) 不变。
2. 蓝色框内的上下长方形，源地址和目的地址相反。
3. 规律：上下地址相反，左右目的(D) 不变！！！

真题1: 上下S，D相反题目

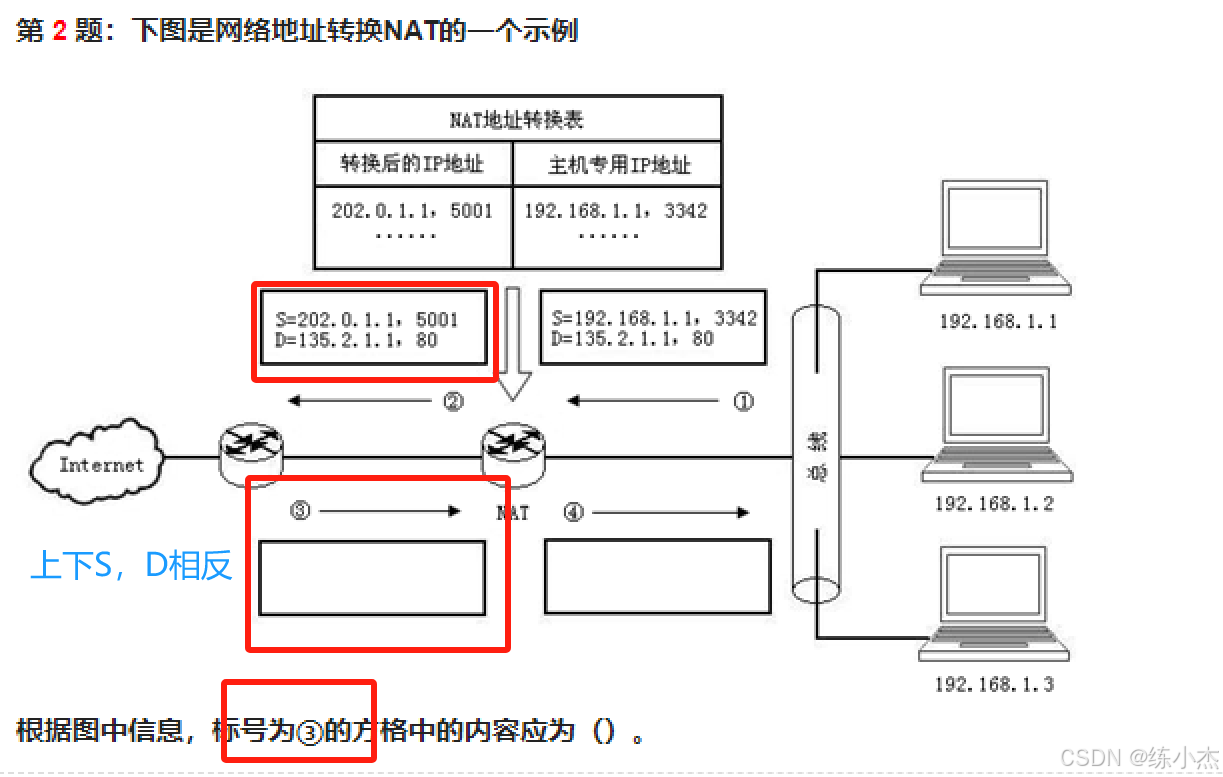
上下地址相反，即标号为③的答案为：
S=135.2.1.1，80
D=202.0.1.1，5001

真题2：先看左右，再看上下

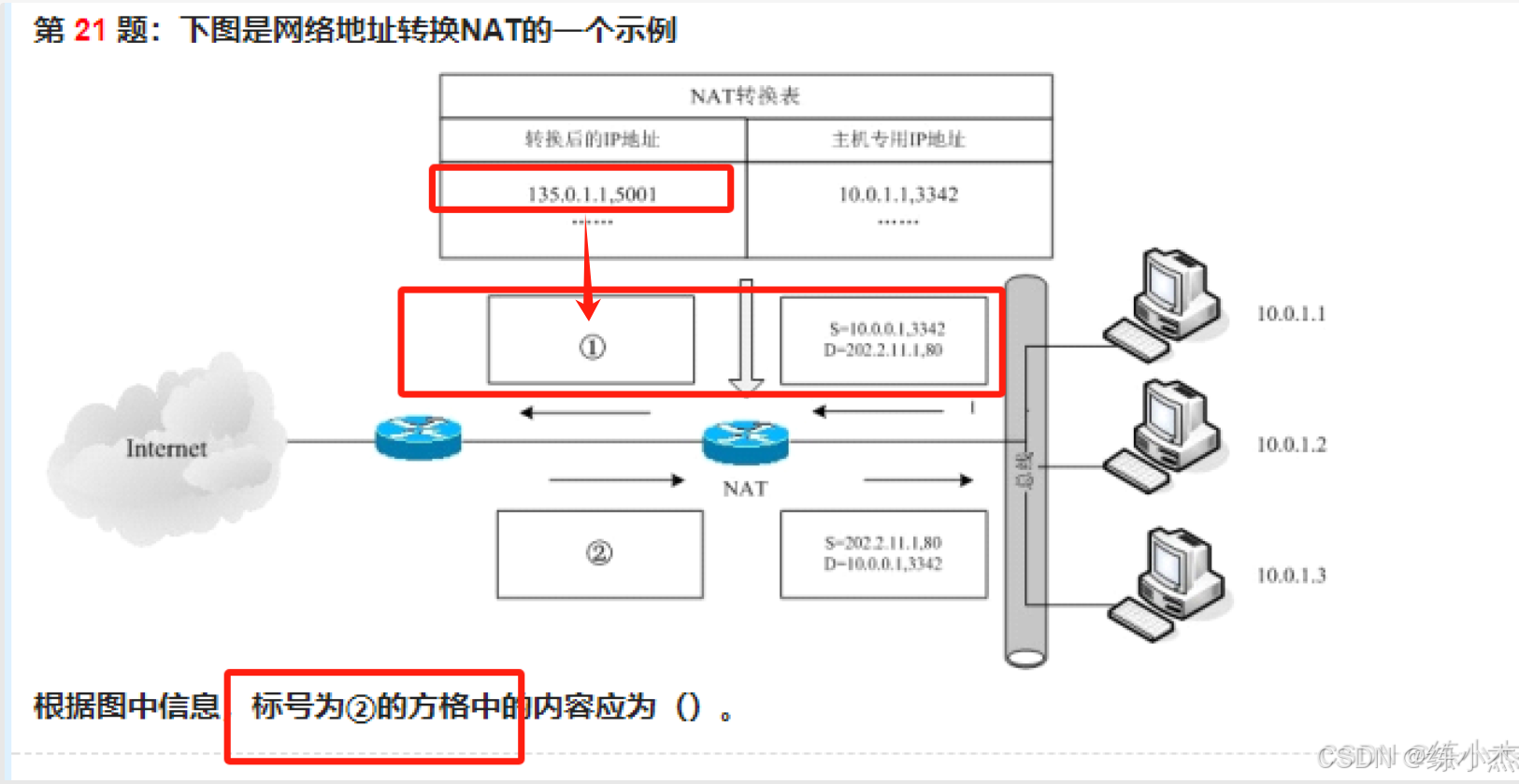
由规律：上下地址相反，左右目的(D) 不变！！！

1. 可以推出①里的：
   S= 135.0.1.1，5001
   D= 202.2.11.1，80
2. 因为上下的S和D相反，则②空为：
   S= 202.2.11.1，80
   D= 135.0.1.1，5001

封装数据包

封装在数据包中的包含目的主机的网络地址(IP地址) 和 下一跳路由的物理地址(即MAC地址)。

情况1：求封装数据包中的目的IP地址和目的MAC地址

目的MAC地址是不断变化的，而目的IP地址不变！！！
封装在数据包③目的IP地址为最后主机的IP地址 223.54.9.2
目的MAC地址： 下一跳的路由的MAC地址 00d0.bcf1.ab14

情况2：求封装数据包中的源IP地址和源MAC地址

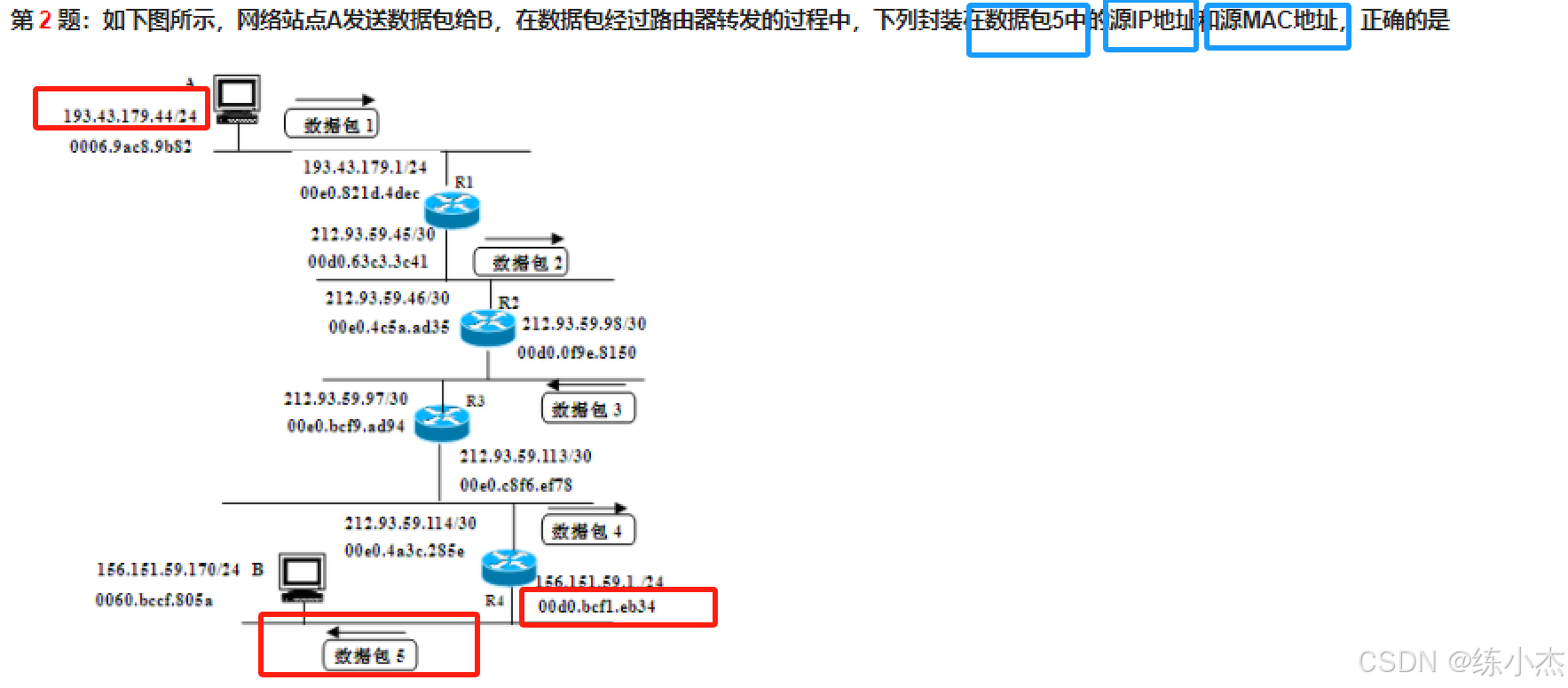
封装在数据包中的 源IP地址不变化，一直是主机A 的IP地址192.43.179.44
源MAC地址数是变化的，这里的数据包⑤经过R4转发，因此，源MAC地址为路由R4的物理地址 00d0.bcf1.eb34

真题实训

题目1：目的IP地址和 目的MAC 地址

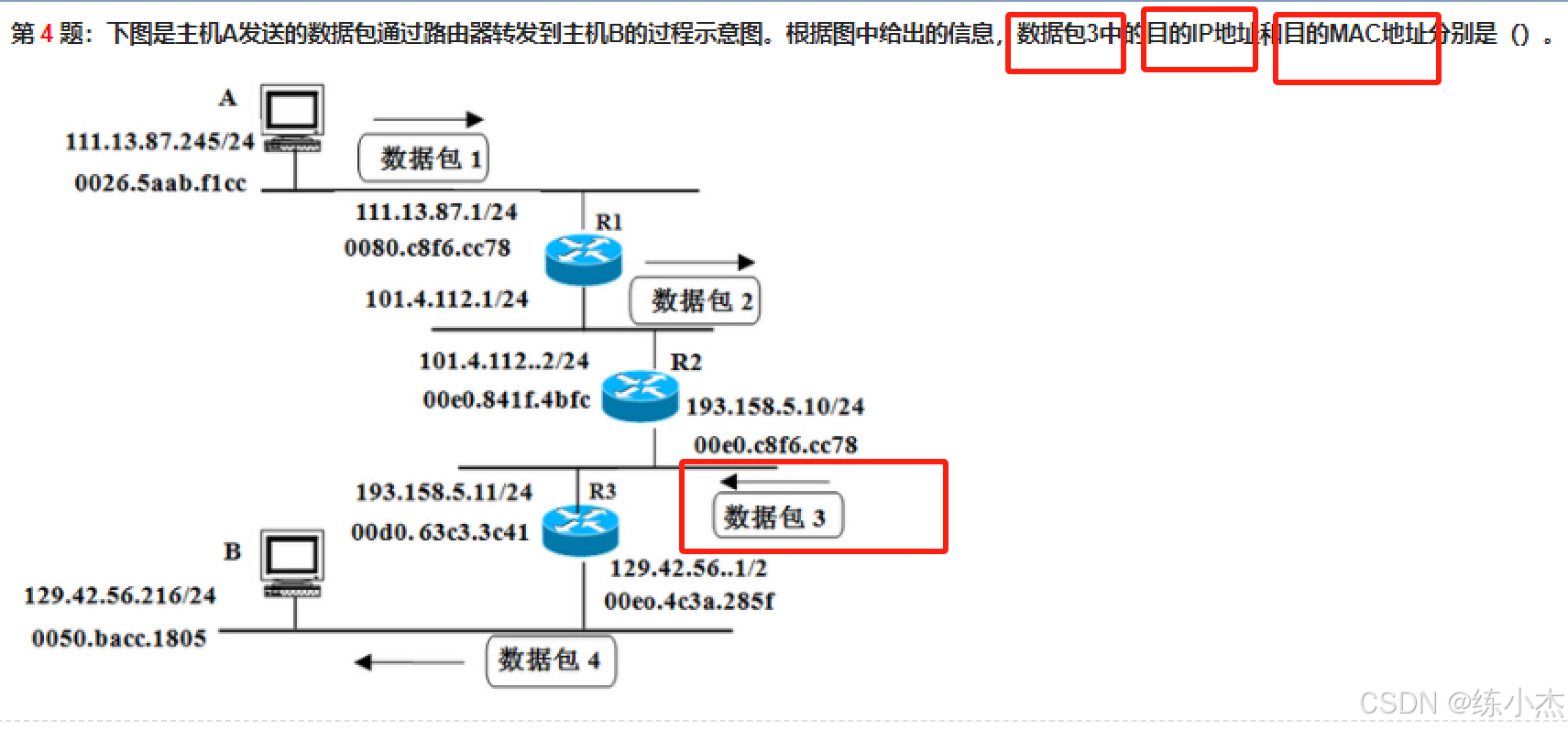
• 答案如下： 选项B

目的IP地址不变，指向最后主机B的IP地址 129.42.56.216
目的MAC地址，对应下一跳路由R3的MAC地址00d0.63c3.3c41

题目2：源IP地址 和 源MAC地址

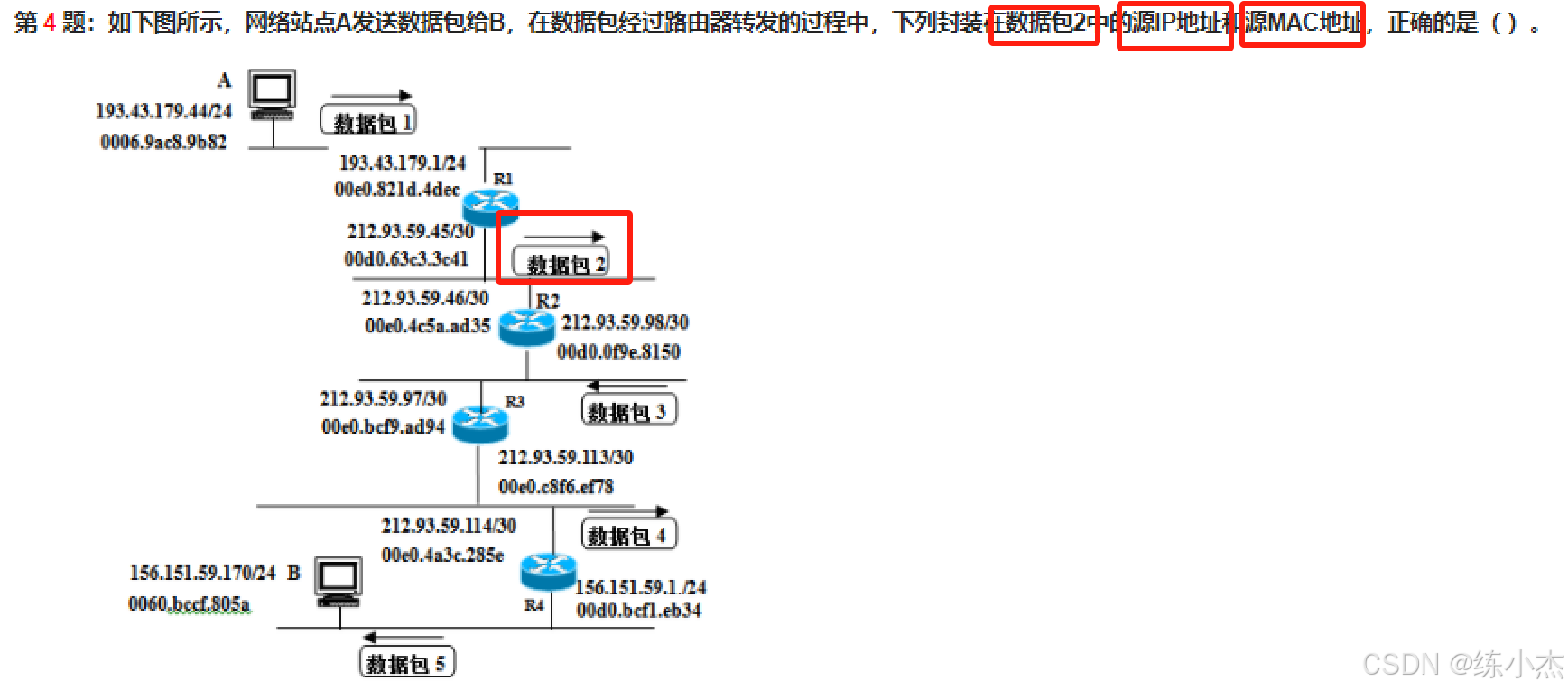
• 答案如下：选项A

源IP地址不变， 主机A的IP地址193.43.179.44
数据包②经路由R1转发，源MAC地址为00d0.63c3.3c41

更新路由表

求更新的路由表距离，即计算采用RIP路由协议的两个相邻路由器(R1,R2)的路由表项数据！！！
其中，有三种情况：

• 第一种：已知R2路由报文、R1更新的路由表项，求R1路由表？(图A)
• 第二种： 已知R1路由表、R1更新的路由表项，求R2路由报文？(图B)
• 第三种：已知R1路由表项、R2路由报文，求R1更新的路由表项？

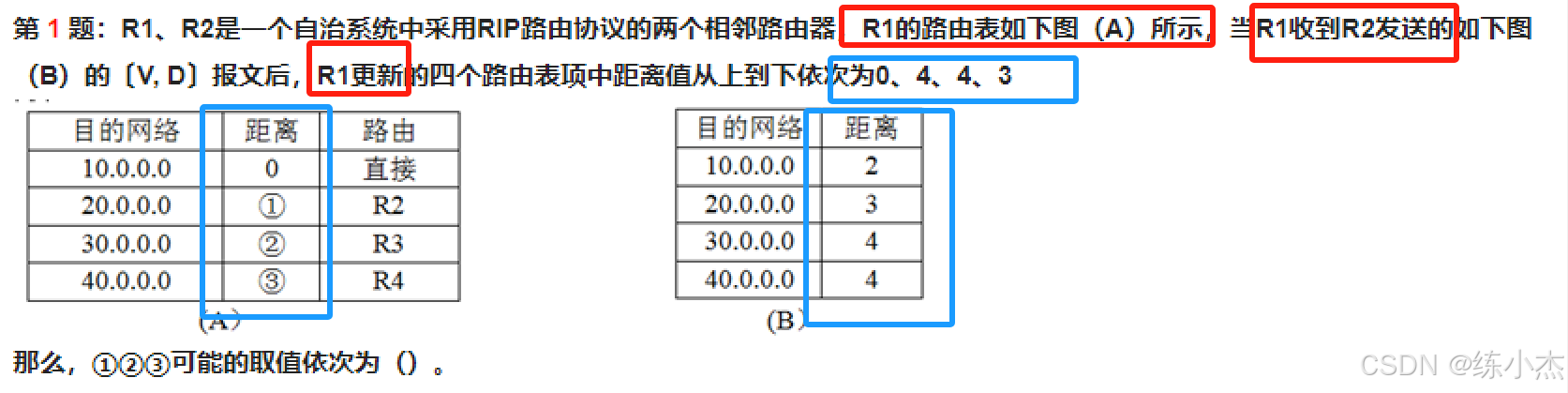
情况一：求图A

已知R2路由报文、R1更新的路由表项，求R1路由表？(图A)

---

计算方法：先列表，把图 B中的距离值都+1，再与R1更新路由表项一一对比，取得较小值，即为A表路由表项范围。
⚠️注意：当两边的表项距离值相等时，取该值即可。例如在4=4时，较小值取 >=4

• 真题示例：
  
• 列表，计算图A范围

B距离+1	图A	R1更新	对比	图A范围
2+1= 3	0	0	0=0	>=0
3+1=4	①	4	4=4	>=4
4+1= 5	②	4	5<4	4
4+1= 5	③	3	5<3	3

• 对比选项，答案为：
  

选择C，即原 A表的距离依次为：0、5、4、3

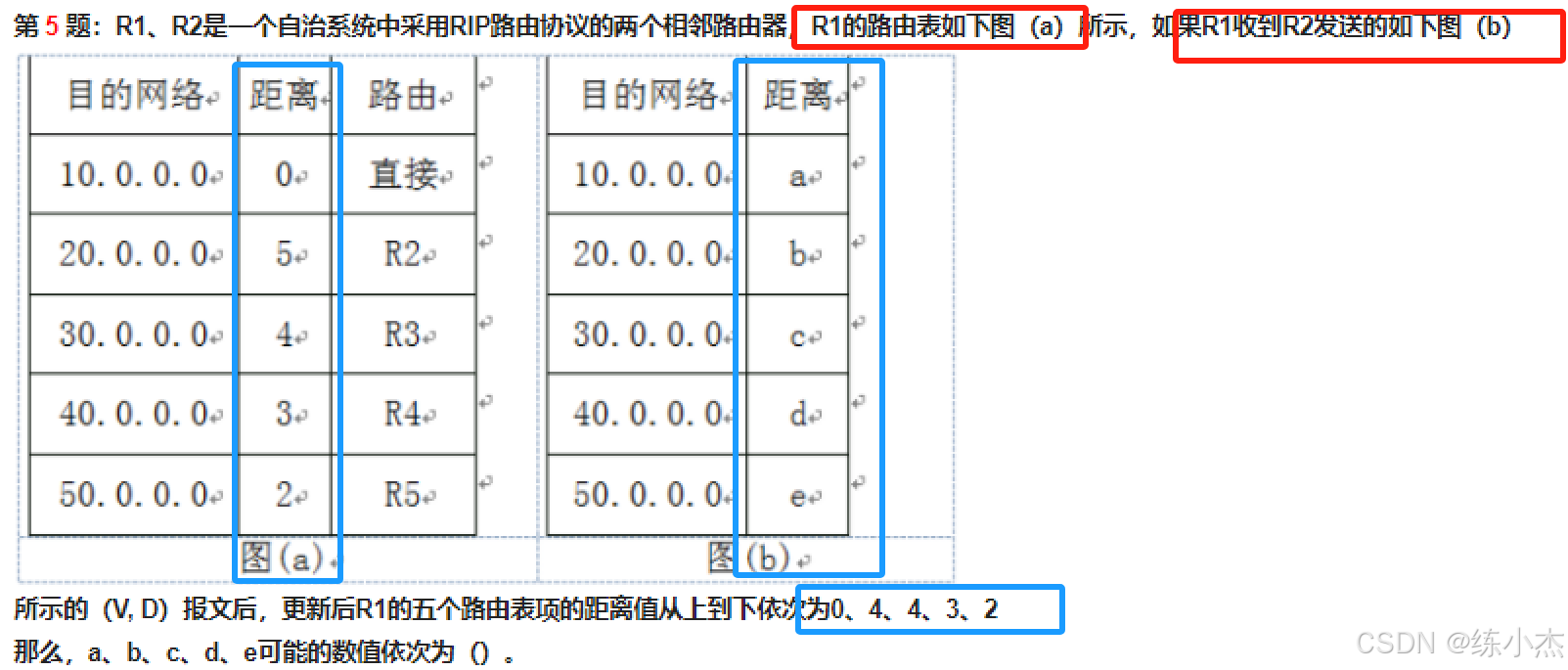
情况二：求图B

已知R1路由表、R1更新的路由表项，求R2路由报文？(图B)

---

计算方法：先列表，把图A 的距离与 R1更新表项一一对比，取得较小值，把较小值的每个距离都减1，即为R2路由报文的范围！！！

⚠️注意：同样，当两边的表项距离值相等时，取该值即可。

• 真题示例：

• 列表，计算图B范围

图A	R1更新	对比	取得较小值	图B范围(较小值-1)
0	0	0=0	0	>= 0
5	4	5>4	4	3
4	4	4=4	>=4	>=3
3	3	3=3	>=3	>=2
2	2	2=2	>=2	>=1

• 对比选项，答案为：

选择B，即图B的距离从上到下依次为：1、3、4、3、1

情况三：求R1更新

已知R1路由表项、R2路由报文，求R1更新的路由表项？

---

计算方法：同样，先列表对比图A和 图B中的距离，当原R1表项中的距离小于 路由表B的距离，R1更新距离不变；若原R1表项中的距离大于 路由表B的距离，则把表B中更小的距离值+1.
⚠️注意：同样，当两边的表项距离值相等时，取该值即可。

• 真题示例：

• 列表对比，并求R1更新范围：

图A	图B	对比	R1更新范围
0	2	0<2	0
5	3	5>3	3+1= 4
4	4	4=4	>=4
3	4	3<4	3
2	1	2>1	1+1= 2

• 对比选项，答案为：

选择B，即R1更新的五个路由表项中距离值为：0、4、4、3、2

---

今天的内容到这里就结束了，有缘再会啦👋
ℹ️了解更多，点击主页【练小杰的CSDN】
⚠️若博客里的内容有问题，欢迎指正，我会及时修改！！！
下周同一时间再见，各位大佬们🚴🏻‍♀️~~