CF每日4题(1500-1700)
经验+4
- 282C 位运算的转化,观察0/1的数量变化
- 704A 用queue模拟
- 1983D 转化题意,找到规律+树状数组求逆序对
- 1061C 二维dp 滚动数组优化
282C 思维 1500

00→0000\rightarrow0000→00
10/01→11,11→01/1010/01\rightarrow 11,11\rightarrow 01/1010/01→11,11→01/10
1可以被合并成一个或裂开成两个,所以只要串中有1,数目和位置就可以随意变换
全是0就不可以凭空变出1来
void solve(){string a,b;cin>>a>>b;int al=a.size(),bl=b.size();int fa=0,fb=0;if(al!=bl)return cout<<"NO"<<endl,void();//长度不同forr(i,1,al)fa+=(a[i-1]=='1');forr(i,1,bl)fb+=(b[i-1]=='1');cout<<((fa&&fb)||(!fa&&!fb)?"YES":"NO")<<endl;//都有1 都没1
}
704A 模拟 1600

自己没写出来,看的题解
const int N=3e5+10,mod=998244353;
struct info
{int id,apd;
};
queue<int>app[N];//单个应用的消息序列
queue<info>lst;//总的消息序列
bool vis[N];//记录消息是否被读过 不要和queue绑定在一起,否则不易修改
void solve(){int n,q;int sm=0,infd=0;//infd消息序号cin>>n>>q;forr(i,1,q){int tp,x;cin>>tp>>x;if(tp==1){//新增消息infd++;app[x].push(infd);lst.push({infd,x});sm++;}else if(tp==2){//删单个应用的所有消息while (app[x].size()){int id=app[x].front();app[x].pop();vis[id]=1;sm--;}}else if(tp==3){//删前x个消息while (lst.size()&&lst.front().id<=x){if(vis[lst.front().id]==0){vis[lst.front().id]=1;app[lst.front().apd].pop();sm--;}lst.pop();//把读过去的都删掉}}cout<<sm<<endl;}
}
1983D 思维 求逆序对 1700

dalao的题解
有一个观察是,交换两个任意位置的数可以看成多次相邻交换。
干脆每次操作都是相邻交换,由于ab两数组同步交换,所以两数组需要交换的奇偶性相等(多出来的操作可以原地tp消耗,只要奇偶性相同就好),就是逆序对数量的奇偶性相等
树状数组求逆序对
const int N=1e5+10,mod=998244353,M=2e5+10;
int n;
int a[N],b[N],tr[N],ta[N],tb[N];
inline int lowbit(int x){return x&-x;
}
void add(int id,int x){for(;id<N;id+=lowbit(id)){tr[id]+=x;}
}
int ask(int id){int ret=0;for(;id>0;id-=lowbit(id))ret+=tr[id];return ret;
}
void solve(){cin>>n;forr(i,1,n){cin>>a[i];ta[i]=a[i];}forr(i,1,n){cin>>b[i];tb[i]=b[i];}sort(ta+1,ta+n+1);sort(tb+1,tb+n+1);forr(i,1,n){if(ta[i]!=tb[i])return no,void();}//树状数组找逆序对O(nlogn)int ra,rb;ra=rb=0;reforr(i,1,n){//从后往前遍历ra+=ask(a[i]-1);//计算后面更小的数add(a[i],1);//添加这个数进去}forr(i,1,n)add(a[i],-1);//清空reforr(i,1,n){rb+=ask(b[i]-1);add(b[i],1);}forr(i,1,n)add(b[i],-1);ra&=1,rb&=1;//取奇偶性cout<<(ra^rb?"no":"yes")<<endl;
}
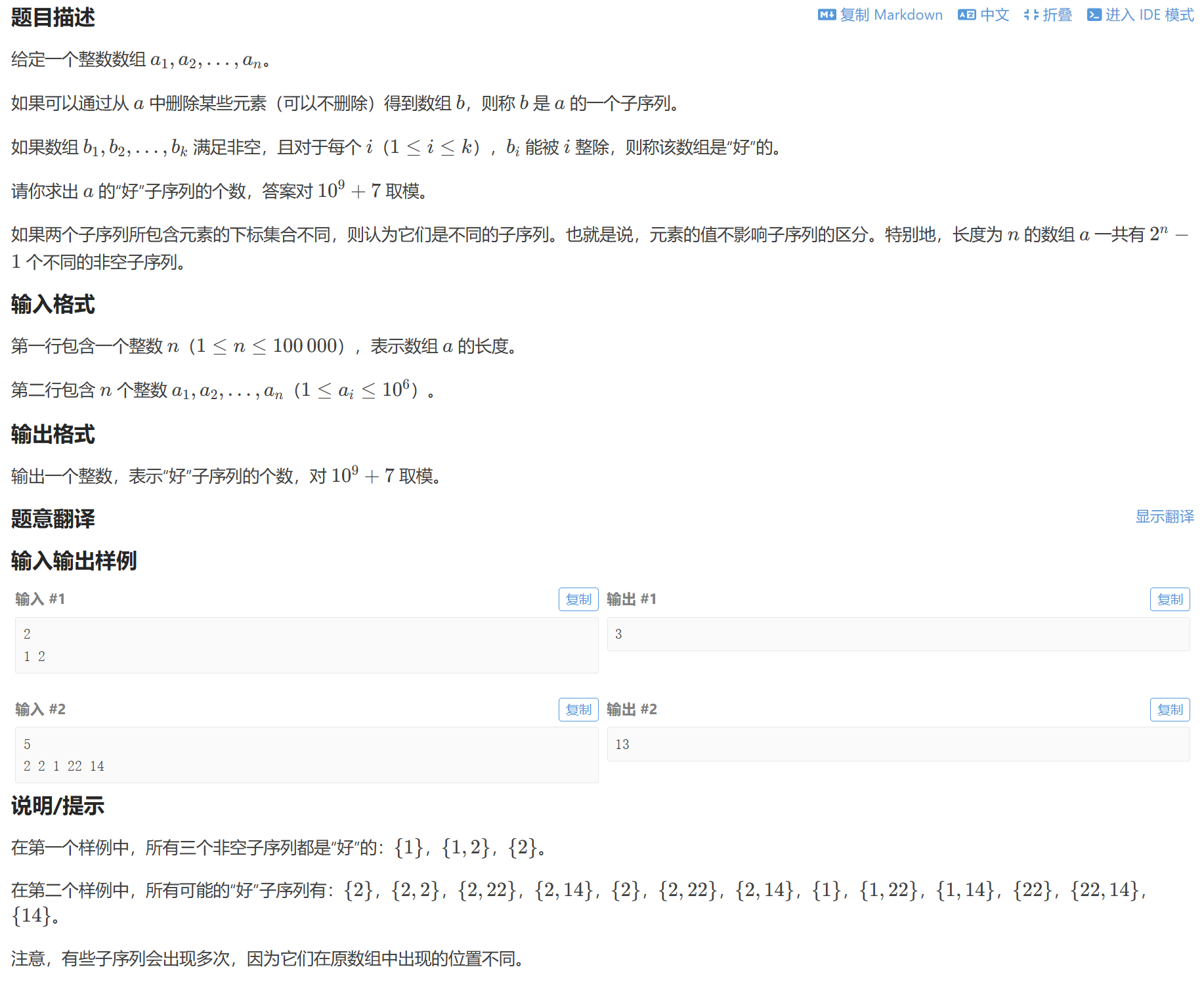
1061C dp 思维 1700
dalao的题解
统计子数组个数,考虑dp
dp[i][j]dp[i][j]dp[i][j]表示前iii个数中,jjj长度子数组好数组的个数
dp[i][j]=dp[i−1][j]+dp[i−1][j−1]⋅(a[i]%j==0)dp[i][j]=dp[i-1][j]+dp[i-1][j-1]\cdot (a[i]\%j==0)dp[i][j]=dp[i−1][j]+dp[i−1][j−1]⋅(a[i]%j==0)
二维数组空间不够,而且O(n2)
发现每个数都是从前一个数转移过来,采用滚动数组
a[i]%j==0a[i]\%j==0a[i]%j==0改变每个a[i]的因数即可dpnew[j]=dp[j]+dp[j−1]dp_{new}[j]=dp[j]+dp[j-1]dpnew[j]=dp[j]+dp[j−1],找n\sqrt nn就够了,时间复杂度O(nn)O(n\sqrt n)O(nn)
const int N=1e6+10,mod=1e9+7,inf=1e9+10;
int dp[N];//注意这里的大小是a_i的范围
void solve(){int n;cin>>n;vector<int>a(n+1);//dp[j] 长度为j的子数组中好数组的个数forr(i,1,n)cin>>a[i];dp[0]=1;vector<int>v;forr(i,1,n){int sq=sqrt(a[i]);forr(j,1,sq){if(a[i]%j==0){v.push_back(j);if(j*j!=a[i]){v.push_back(a[i]/j);}}}sort(v.begin(),v.end(),greater<int>());for(auto j:v){dp[j]=(dp[j]+dp[j-1])%mod;}v.clear();}int ans=0;forr(i,1,n)ans=(ans+dp[i])%mod;cout<<ans<<endl;
}
