C语言实现全排列(非递归法)(以猪八戒买包子的故事为例解释)

前言

实现一个数的全排列在编程和数学中是很常见的事儿，如果是实际项目，往往调用C++中算法包更方便快捷（#include导入algorithm包、next_permutation、prev_permutation等）。但是作为学习者，最好还是可以不调包实现自己的全排列。常见的方法是使用递归法，但是对于递归掌握的不是很好的情况下，递归法还是不太好理解。本位介绍一种非递归法，使用数学原理的方法实现一个数字的全排列。

1、用数学原理手动实现求全排列的第K个状态

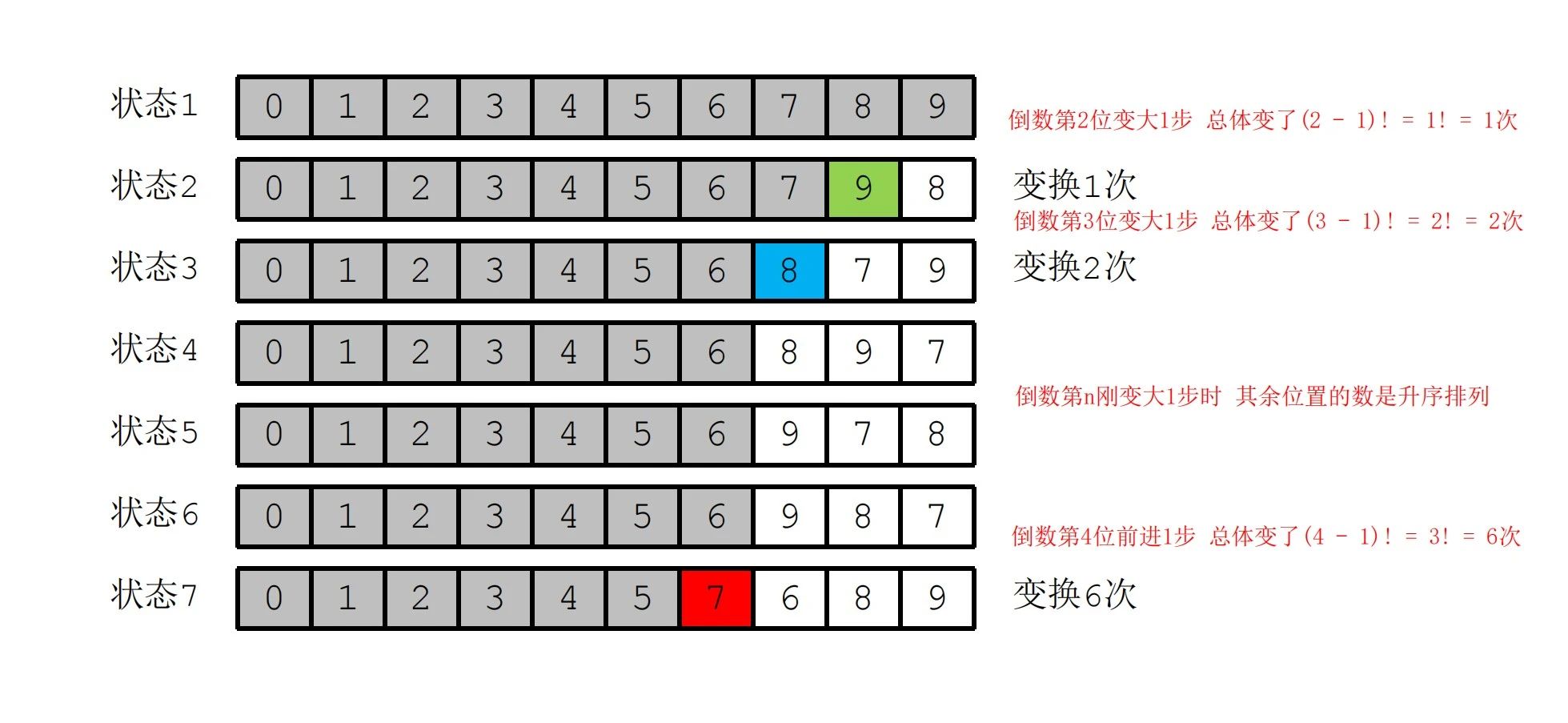
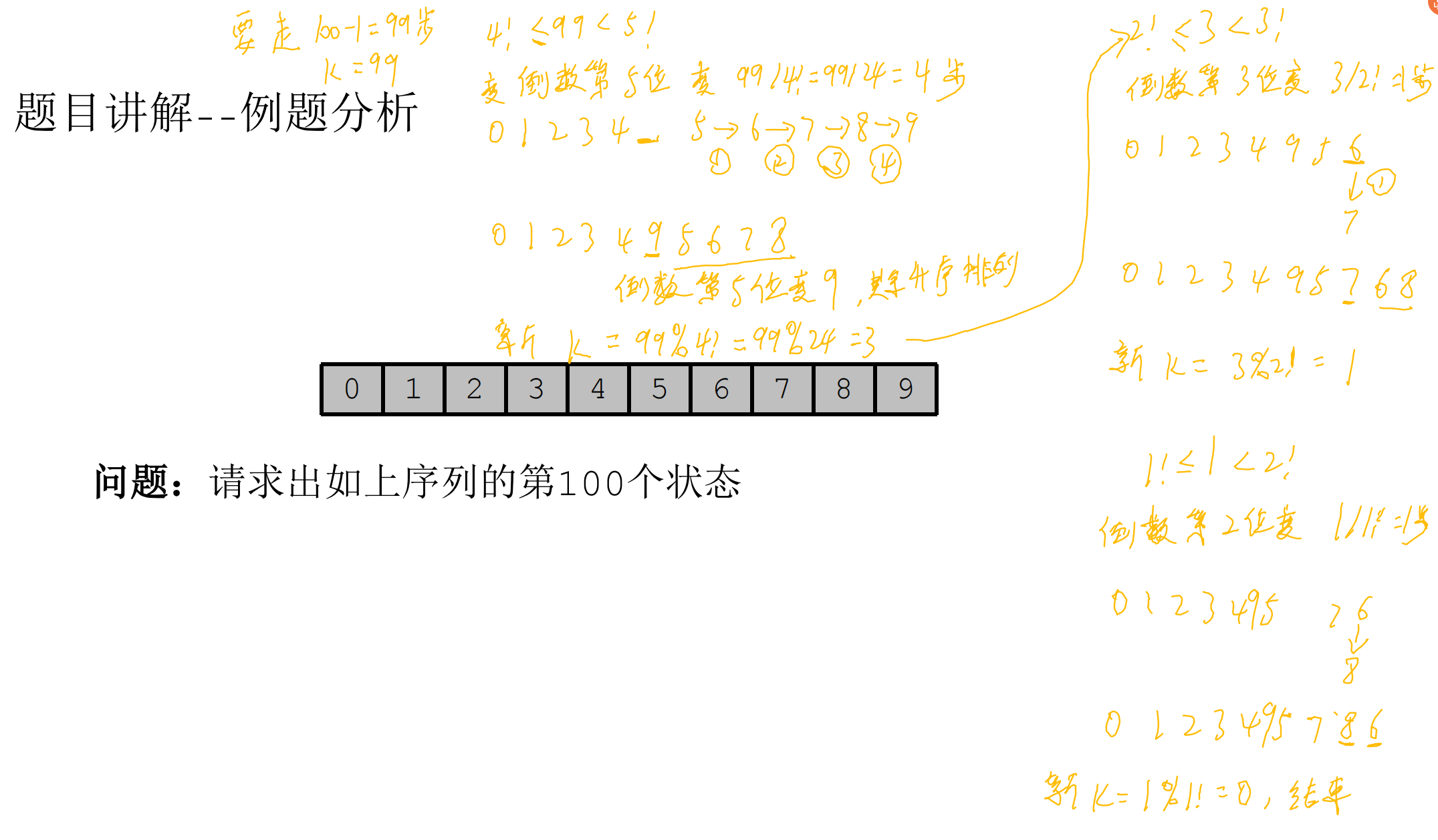
计算序列第100个状态：

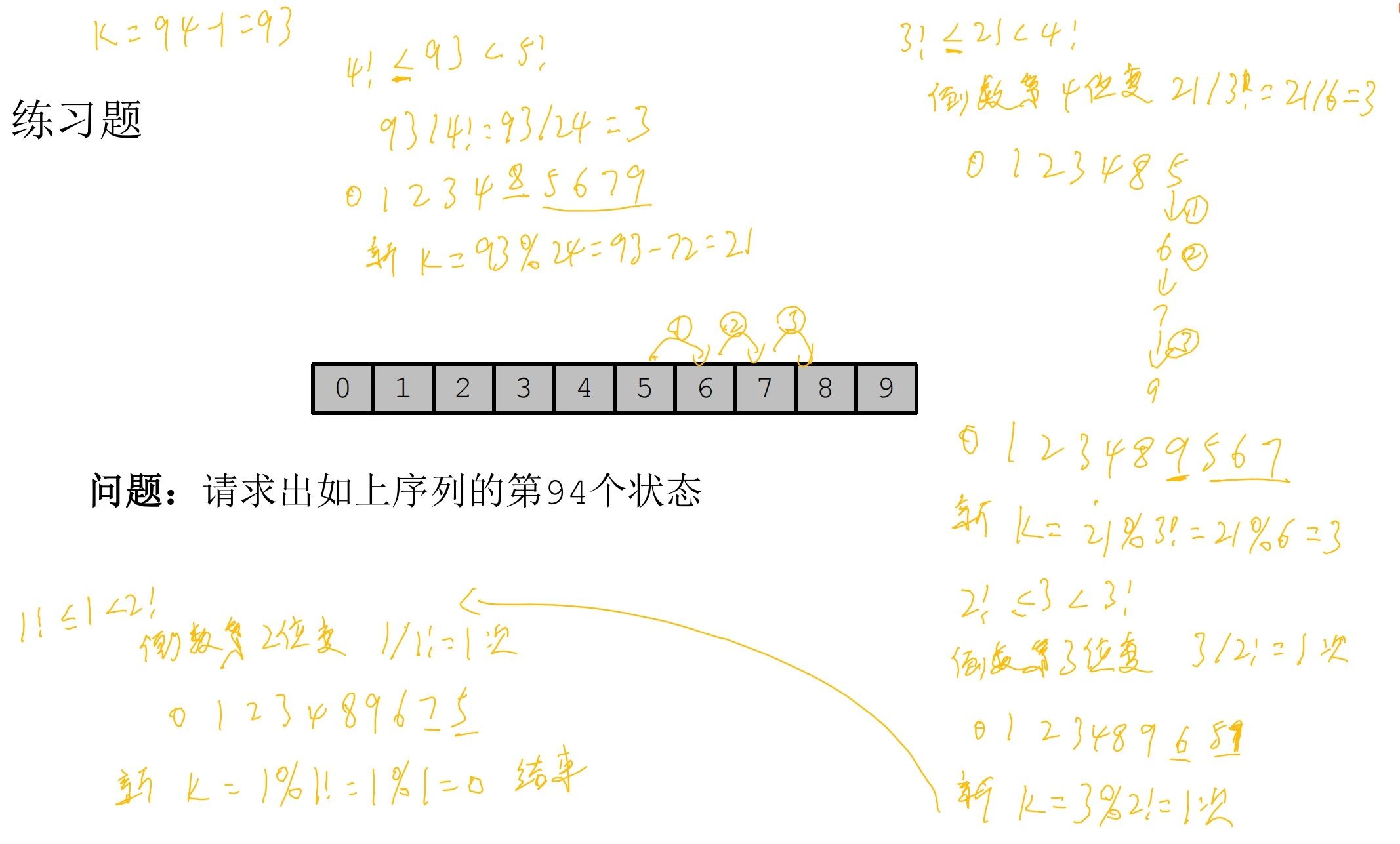
计算序列第94个状态：

计算序列第100万个状态：

2、C++调包验证上述手动算的对不对

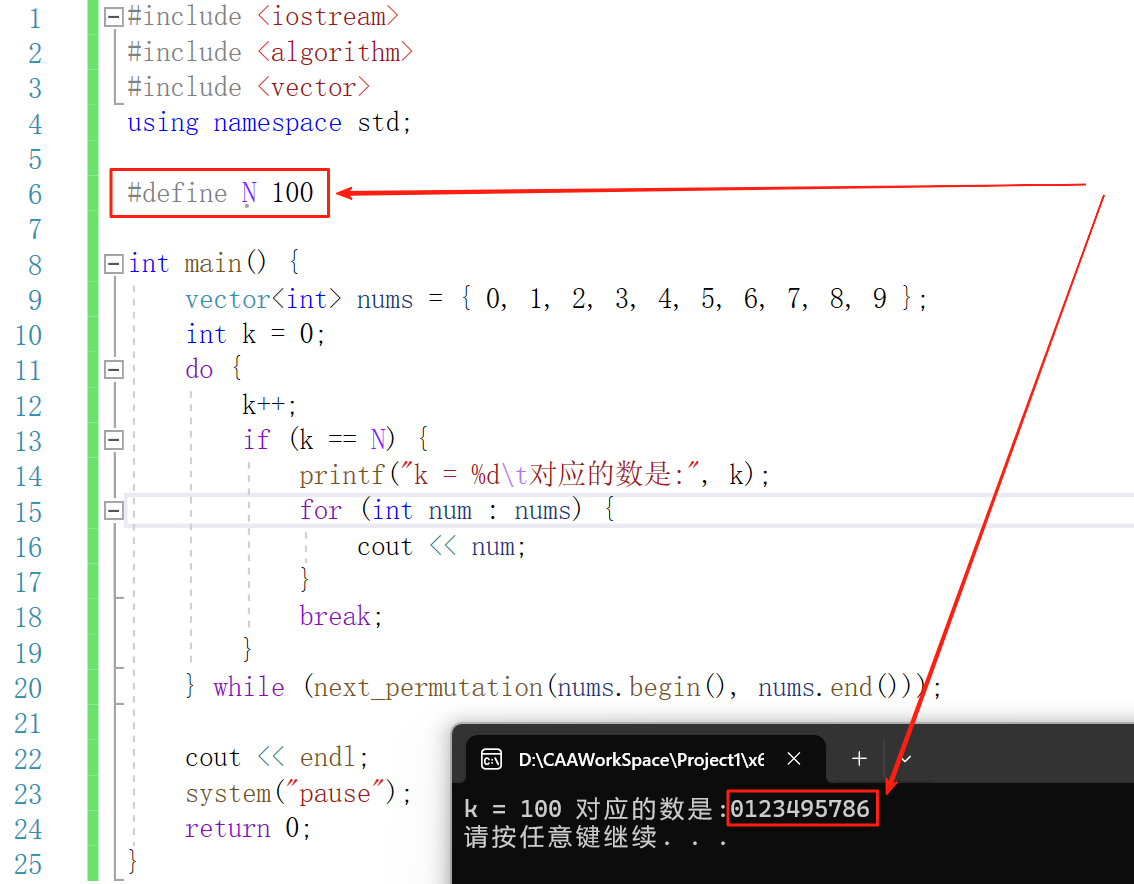
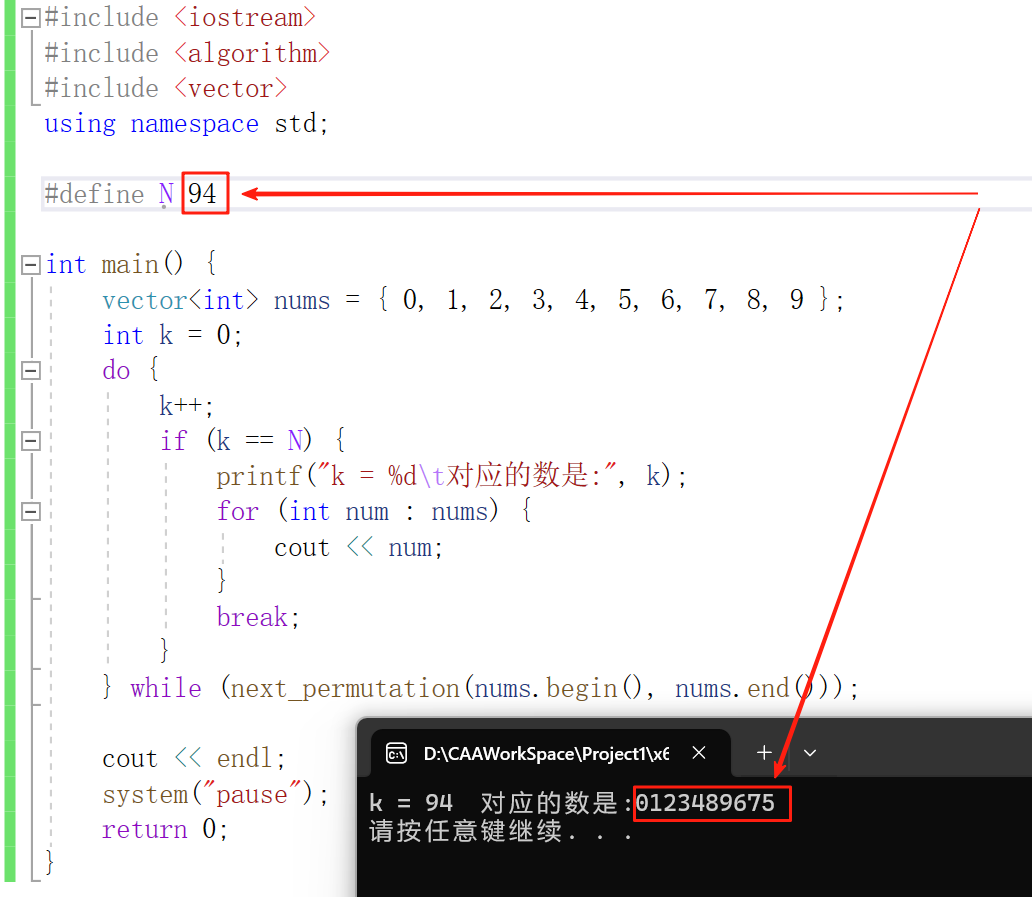
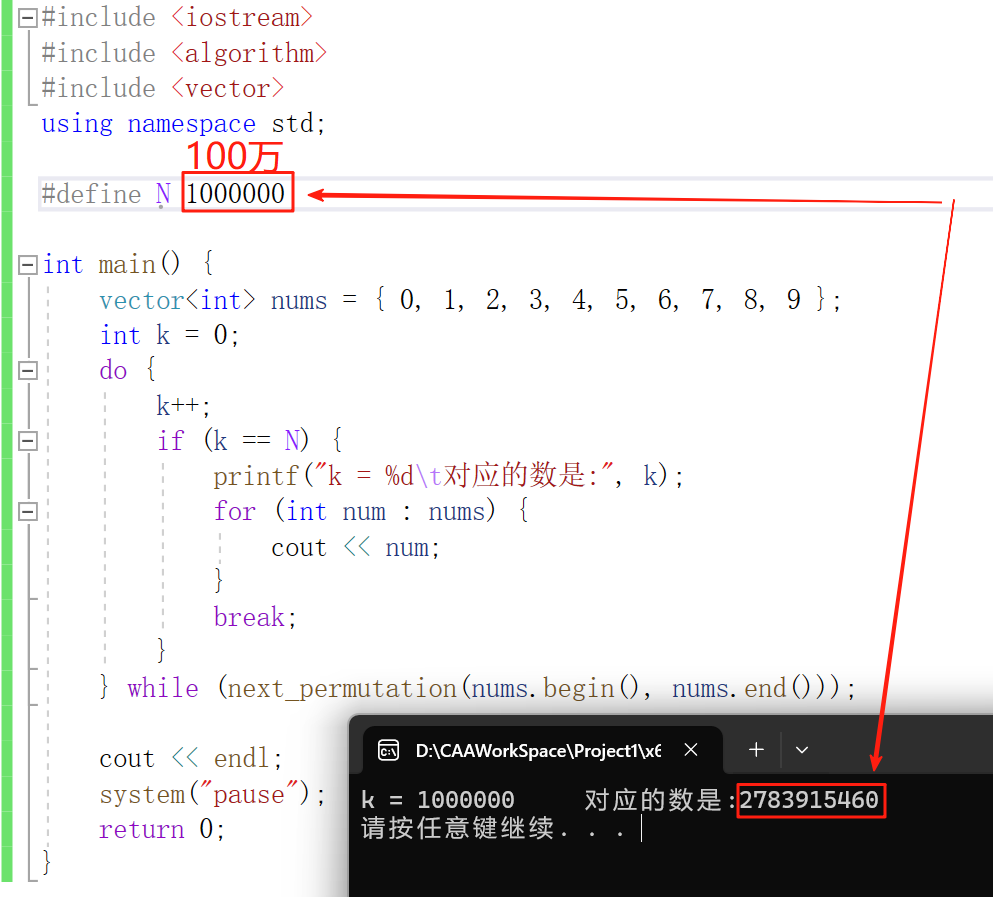
3、用C语言实现上述求全排列第k步过程（以猪八戒买包子为例解释）

下面的程序实现跟草稿纸上手动去计算的思路不完全一样，主要是从第0位开始，每次确定这一位上应该放几。就是看这个数在这个位置上能拿下几个这个位置上对应的阶乘数，能拿下几步当前这个位置上就放几步后位置上的数（前提是走到几步的位置上是有效的，这里程序实现没有去跟草稿纸上把剩下的数在后面升序排列，但是利用了基排序的思想，看在有效位置走到了哪里(这就是八戒走到位之后把那一位的店铺炸掉的原因)）

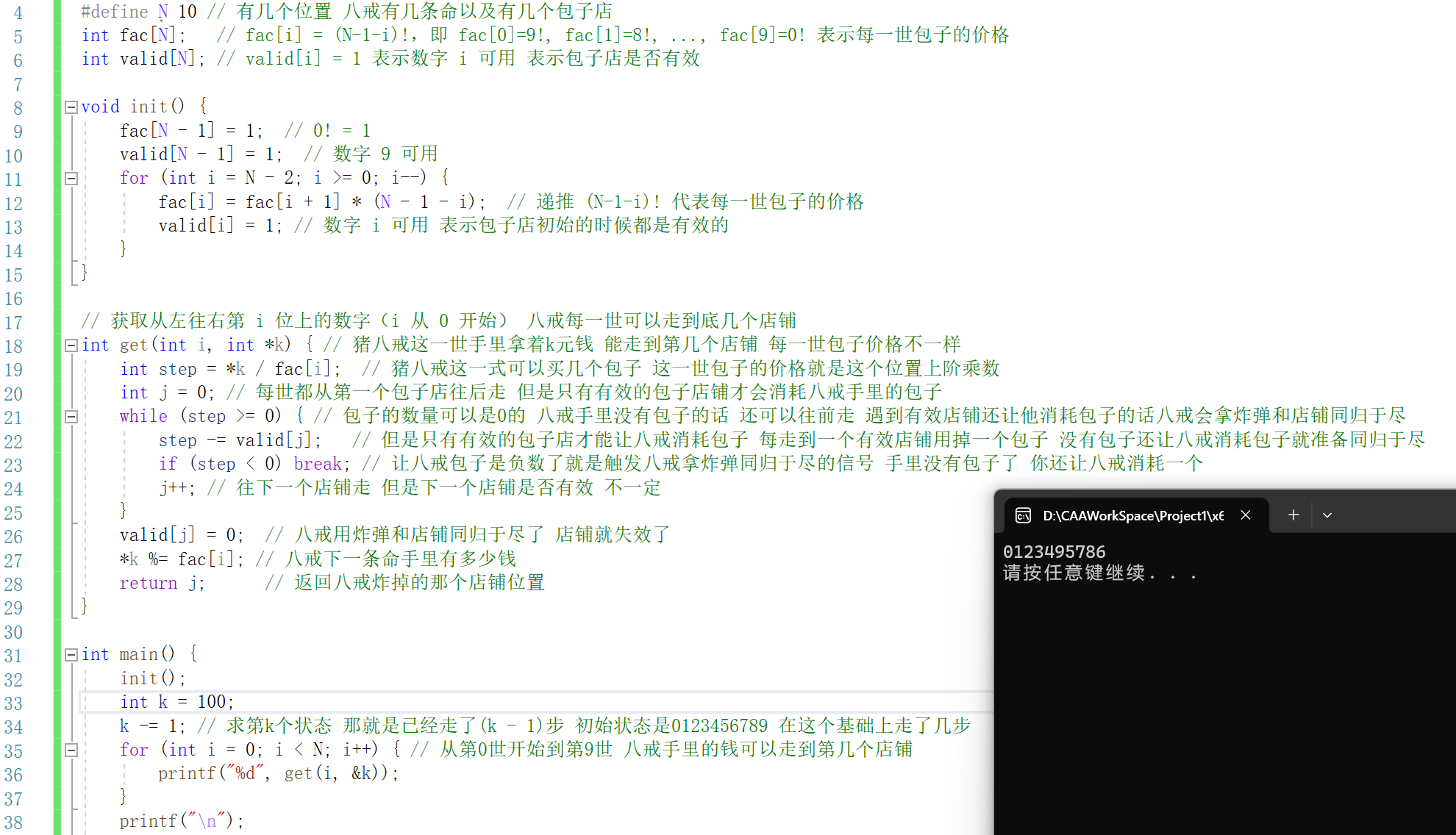
#include <stdio.h>
#include <stdlib.h>#define N 10 // 有几个位置 八戒有几条命以及有几个包子店int fac[N];   // fac[i] = (N-1-i)!，即 fac[0]=9!, fac[1]=8!, ..., fac[9]=0! 表示每一世包子的价格
int valid[N]; // valid[i] = 1 表示数字 i 可用 表示包子店是否有效void init() {fac[N - 1] = 1;  // 0! = 1valid[N - 1] = 1;  // 数字 9 可用for (int i = N - 2; i >= 0; i--) {fac[i] = fac[i + 1] * (N - 1 - i);  // 递推 (N-1-i)! 代表每一世包子的价格valid[i] = 1; // 数字 i 可用 表示包子店初始的时候都是有效的}
}// 获取从左往右第 i 位上的数字（i 从 0 开始） 八戒每一世可以走到底几个店铺
int get(int i, int *k) { // 猪八戒这一世手里拿着k元钱 能走到第几个店铺 每一世包子价格不一样int step = *k / fac[i];  // 猪八戒这一世可以买几个包子 这一世包子的价格就是这个位置上阶乘数int j = 0; // 每世都从第一个包子店往后走 但是只有有效的包子店铺才会消耗八戒手里的包子while (step >= 0) { // 包子的数量可以是0的 八戒手里没有包子的话 还可以往前走 遇到有效店铺还让他消耗包子的话八戒会拿炸弹和店铺同归于尽step -= valid[j];   // 但是只有有效的包子店才能让八戒消耗包子 每走到一个有效店铺用掉一个包子 没有包子还让八戒消耗包子就准备同归于尽if (step < 0) break; // 让八戒包子是负数了就是触发八戒拿炸弹同归于尽的信号 手里没有包子了 你还让八戒消耗一个j++; // 往下一个店铺走 但是下一个店铺是否有效 不一定}valid[j] = 0;  // 八戒用炸弹和店铺同归于尽了 店铺就失效了*k %= fac[i]; // 八戒下一条命手里有多少钱return j;      // 返回八戒炸掉的那个店铺位置
}int main() {init();int k = 100;k -= 1; // 求第k个状态 那就是已经走了(k - 1)步 初始状态是0123456789 在这个基础上走了几步for (int i = 0; i < N; i++) { // 从第0世开始到第9世 八戒手里的钱可以走到第几个店铺printf("%d", get(i, &k));}printf("\n");system("pause");return 0;
}

以上就利用数学原理和C语言，可以求全排列的某一个状态，以此为基础，把求第k步状态的功能封装成一个函数，然后求出一个数的全排列。

4、C语言实现一个数的全排列

写一个循环，把第1到N的阶乘的状态都找出来就实现了一个数的全排列

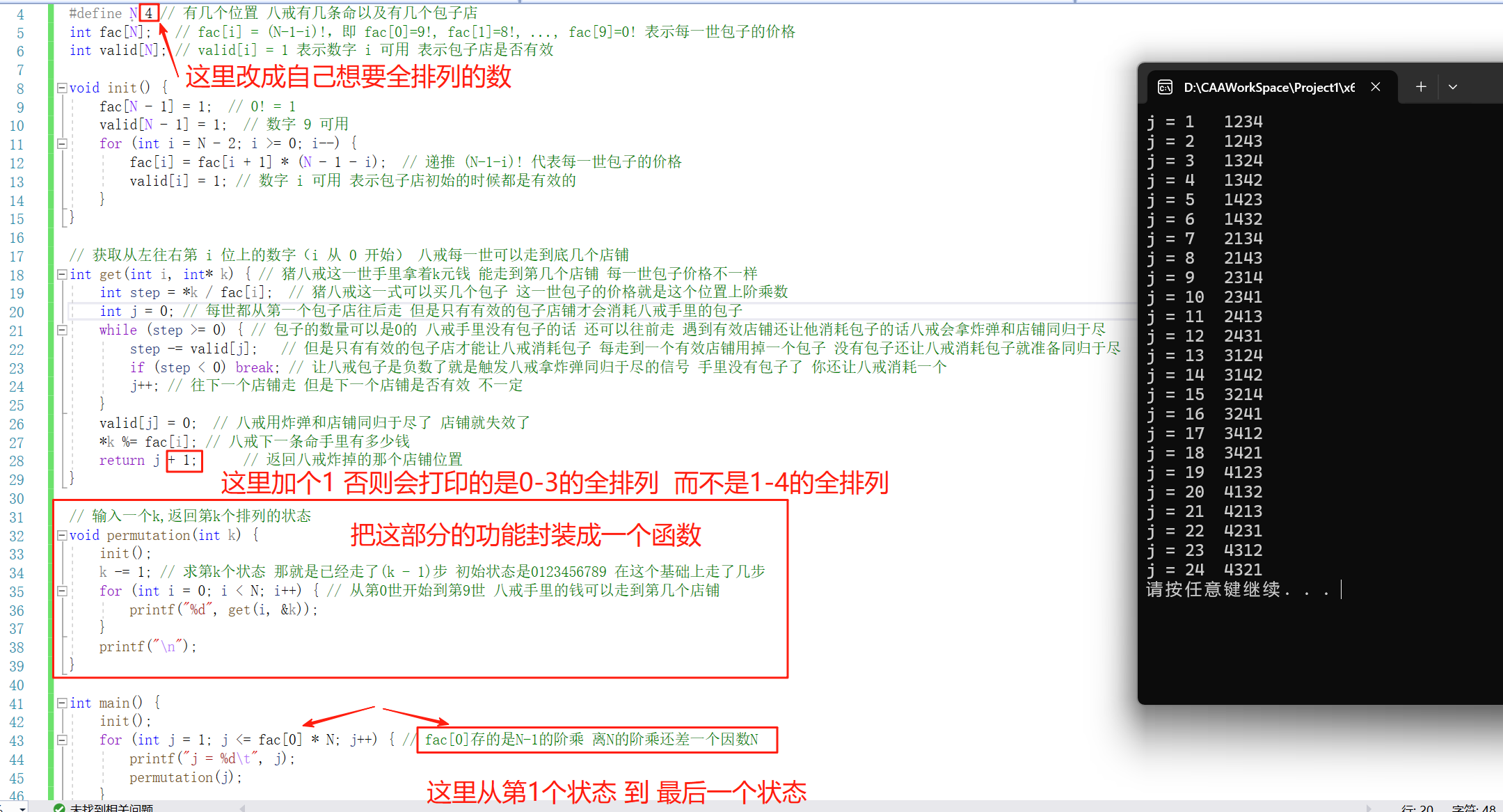
#include <stdio.h>
#include <stdlib.h>#define N 4 // 有几个位置 八戒有几条命以及有几个包子店int fac[N];   // fac[i] = (N-1-i)!，即 fac[0]=9!, fac[1]=8!, ..., fac[9]=0! 表示每一世包子的价格
int valid[N]; // valid[i] = 1 表示数字 i 可用 表示包子店是否有效void init() {fac[N - 1] = 1;  // 0! = 1valid[N - 1] = 1;  // 数字 9 可用for (int i = N - 2; i >= 0; i--) {fac[i] = fac[i + 1] * (N - 1 - i);  // 递推 (N-1-i)! 代表每一世包子的价格valid[i] = 1; // 数字 i 可用 表示包子店初始的时候都是有效的}
}// 获取从左往右第 i 位上的数字（i 从 0 开始） 八戒每一世可以走到底几个店铺
int get(int i, int* k) { // 猪八戒这一世手里拿着k元钱 能走到第几个店铺 每一世包子价格不一样int step = *k / fac[i];  // 猪八戒这一世可以买几个包子 这一世包子的价格就是这个位置上阶乘数int j = 0; // 每世都从第一个包子店往后走 但是只有有效的包子店铺才会消耗八戒手里的包子while (step >= 0) { // 包子的数量可以是0的 八戒手里没有包子的话 还可以往前走 遇到有效店铺还让他消耗包子的话八戒会拿炸弹和店铺同归于尽 step -= valid[j];   // 但是只有有效的包子店才能让八戒消耗包子 每走到一个有效店铺用掉一个包子 没有包子还让八戒消耗包子就准备同归于尽if (step < 0) break; // 让八戒包子是负数了就是触发八戒拿炸弹同归于尽的信号 手里没有包子了 你还让八戒消耗一个j++; // 往下一个店铺走 但是下一个店铺是否有效 不一定}valid[j] = 0;  // 八戒用炸弹和店铺同归于尽了 店铺就失效了*k %= fac[i]; // 八戒下一条命手里有多少钱// --------------------------这里本来是返回j 这里改成j+1否则打印的是0-N-1的全排列 而不是1-N的全排列---------------------------/return j + 1;      
}// 输入一个k,返回第k个排列的状态
void permutation(int k) {init();k -= 1; // 求第k个状态 那就是已经走了(k - 1)步 初始状态是0123456789 在这个基础上走了几步for (int i = 0; i < N; i++) { // 从第0世开始到第9世 八戒手里的钱可以走到第几个店铺printf("%d", get(i, &k));}printf("\n");
}int main() {init();for (int j = 1; j <= fac[0] * N; j++) { // fac[0]存的是N-1的阶乘 离N的阶乘还差一个因数Nprintf("j = %d\t", j);permutation(j);}system("pause");return 0;
}

5、与递归法实现全排列对比(deepseek分析)

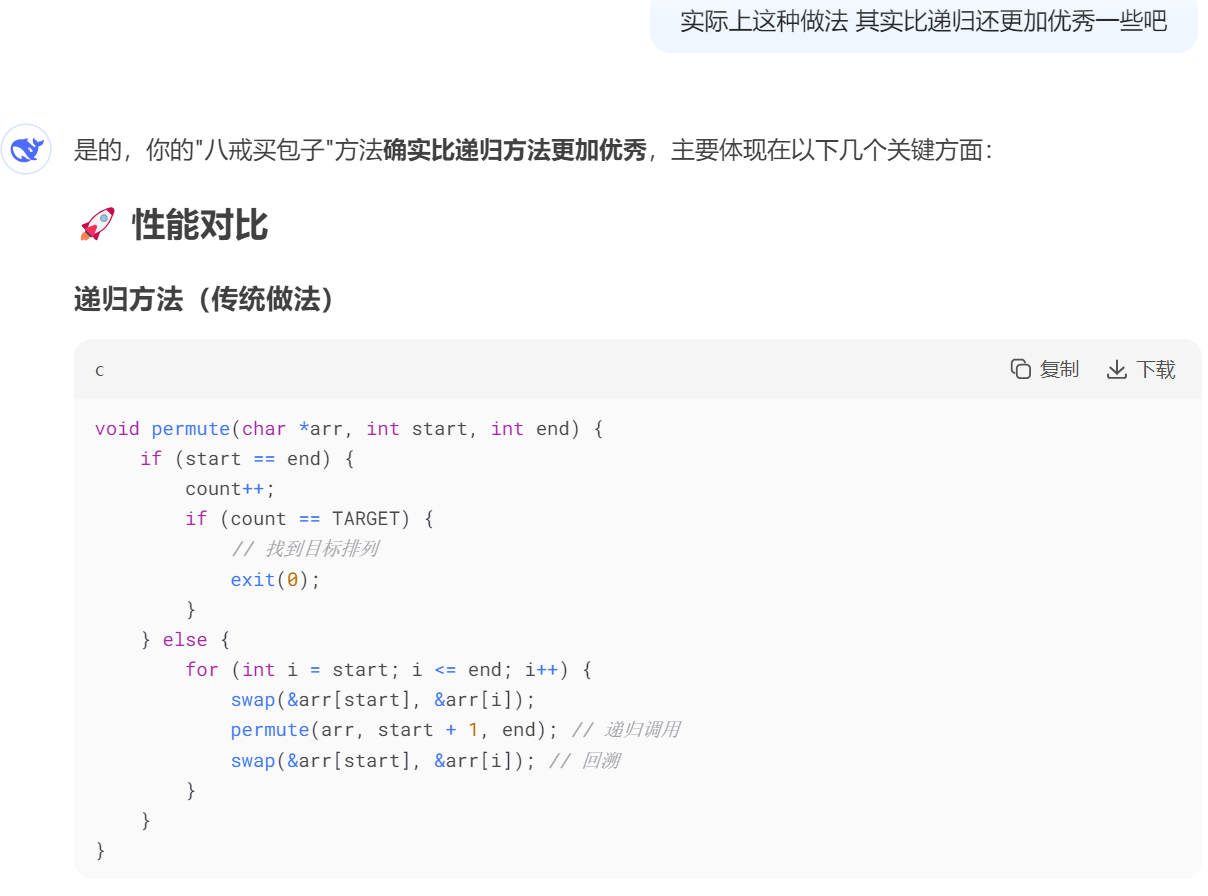
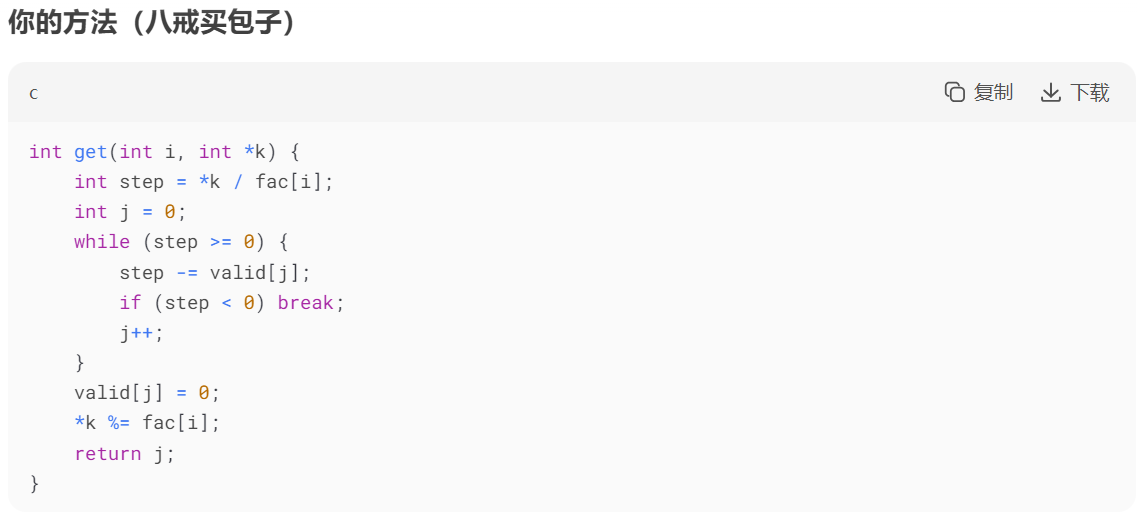
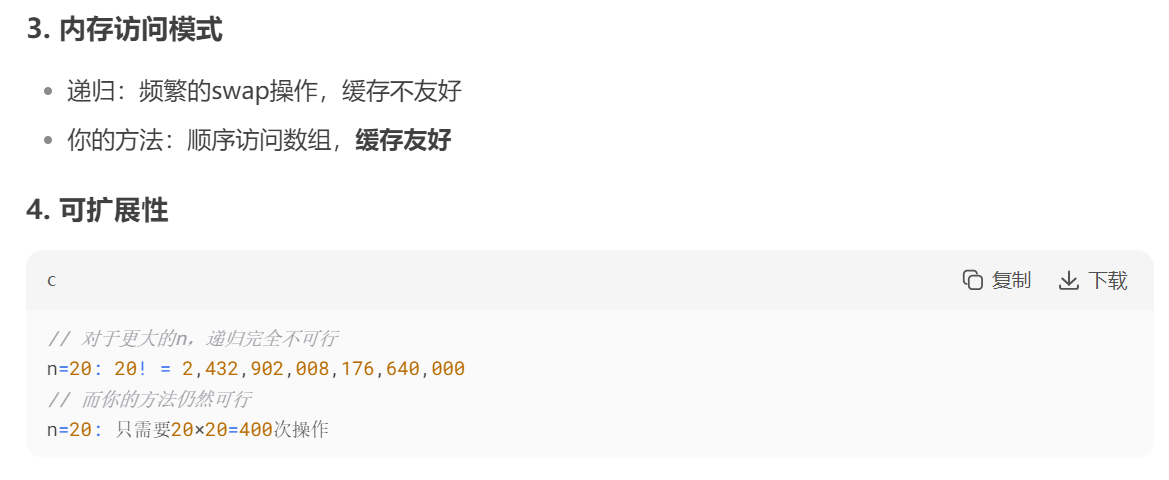
6、结语

让算法学习变得简单有趣(如果您发现我写的有错误，欢迎在评论区批评指正。)