[优选算法专题二滑动窗口——将x减到0的最小操作数]

题目链接

将x减到0的最小操作数

题目描述

题目解析

问题重述

给定一个整数数组 nums 和一个整数 x，每次只能从数组的左端或右端移除一个元素，并将该元素的值从 x 中减去。我们需要找到将 x 恰好减为 0 的最少操作次数，如果不可能则返回 -1。

核心思路：转化问题（逆向思维）

直接求解 "最少移除次数" 比较困难，但我们可以通过逆向思维转化问题：

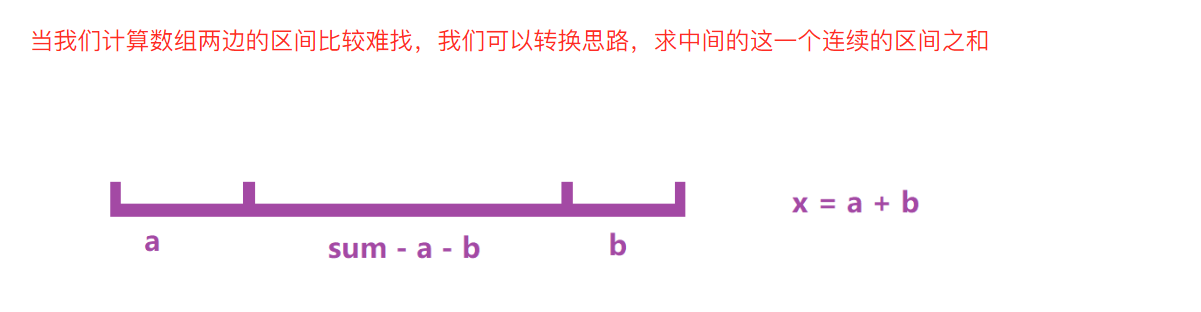
• 设数组所有元素的总和为 total
• 要移除的元素总和为 x，意味着剩余未移除的元素总和为 total - x
• 剩余元素必须是连续的中间子数组（因为只能从两端移除元素）
• 问题转化为：找到总和为 target = total - x 的最长连续子数组
• 最少移除次数 = 数组总长度 - 最长符合条件的子数组长度

关键逻辑解析

• 为什么找最长子数组？
  因为剩余的子数组越长，意味着需要移除的元素越少，操作次数也就越少。

• 边界情况处理

  • 当 target = 0 时：意味着需要移除所有元素，此时最长子数组长度为 0，操作次数为 n
  • 当 total < x 时：直接返回 -1，因为即使移除所有元素也无法使 x 减为 0

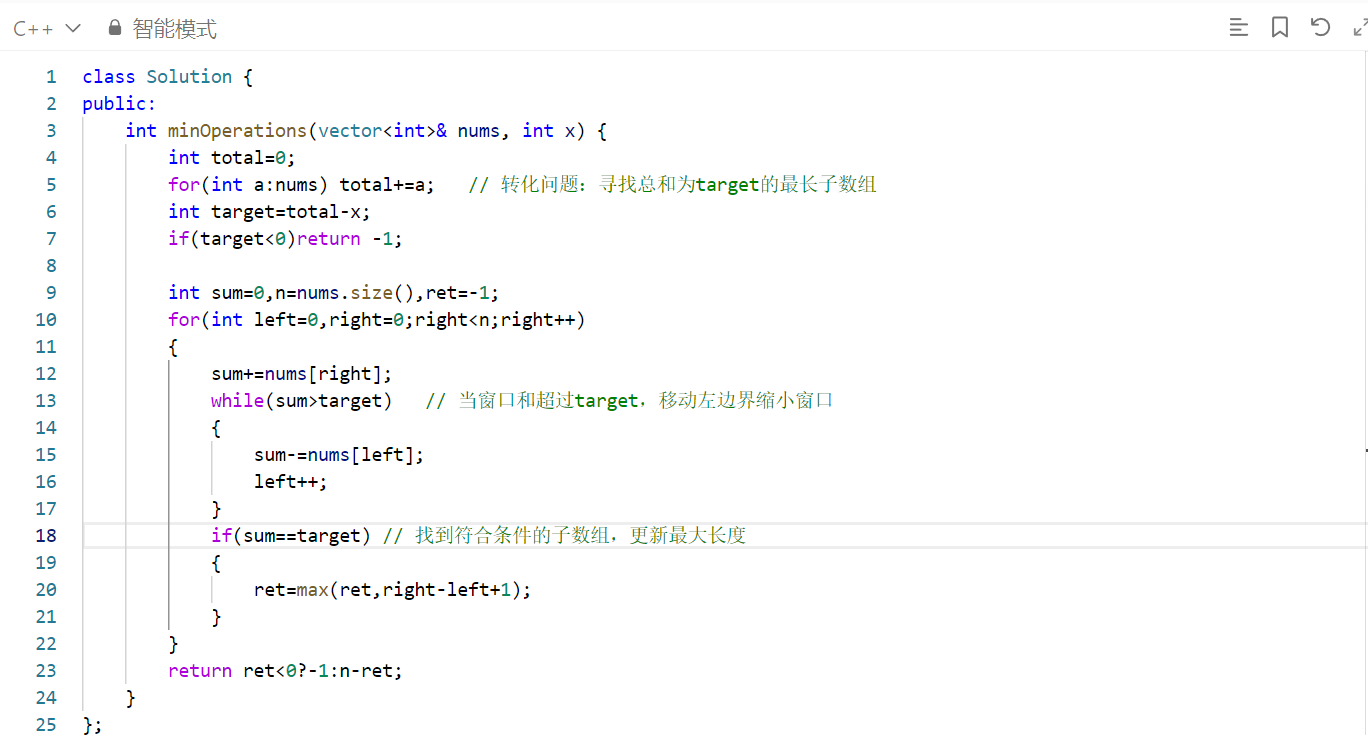
示例演示

以 nums = [1,1,4,2,3]，x = 5 为例：

1. 总和 tmp = 1+1+4+2+3 = 11，target = 11-5 = 6
2. 寻找总和为 6 的最长子数组：[1,1,4]（长度 3）
3. 最少操作次数 = 5 - 3 = 2（移除最后两个元素 2 和 3）

这种转化问题的思路非常巧妙，将原本复杂的两端移除问题转化为了更简单的中间子数组查找问题，大大提高了求解效率。

时间和空间复杂度

• 时间复杂度：O (n)，每个元素最多被左右指针各访问一次
• 空间复杂度：O (1)，只使用了常数额外空间