当前位置： 首页 > news >正文

掌握MATLAB三维可视化：从基础到实战技巧

news 2025/8/15 8:16:26

目录

1. 引言：三维可视化的重要性

2. 基础三维图形绘制

2.1 三维曲线图（plot3）

2.2 三维散点图（scatter3）

2.3 三维网格图（mesh）

2.4 三维曲面图（surf）

3. 参数曲面绘制

4. 三维等值面可视化

5. 高级三维可视化

5.1 矢量场可视化（quiver3）

5.2 三维流线图（streamline）

5.3 圆锥体图（coneplot）

6. 光照与材质处理

7. 交互式操作与视角控制

8. 三维可视化应用实例

8.1 分子结构可视化

8.2 地形可视化

9. 结语

1. 引言：三维可视化的重要性

在科学计算、工程分析和数据可视化领域，三维图形能够直观展示复杂数据的内在结构和空间关系。MATLAB作为科学计算领域的标准工具，提供了强大的三维可视化功能，可帮助研究人员和工程师：

  • 直观展示复杂数学模型和计算结果

  • 分析三维空间中的物理现象（如流体力学、电磁场）

  • 可视化医学成像数据（如CT、MRI扫描）

  • 创建高质量的科学出版物图表

  • 探索高维数据集的空间分布特征

本文将系统介绍MATLAB中各种三维可视化技术，并通过具体代码示例展示其应用。

2. 基础三维图形绘制

2.1 三维曲线图（plot3）

plot3函数是三维空间中绘制曲线的理想选择，类似于二维的plot函数。

% 绘制螺旋线
t = 0:pi/50:10*pi;
x = sin(t);
y = cos(t);
z = t;figure;
plot3(x, y, z, 'b-', 'LineWidth', 2);
grid on;
xlabel('X轴');
ylabel('Y轴');
zlabel('Z轴');
title('三维螺旋线');
view(30, 45); % 设置视角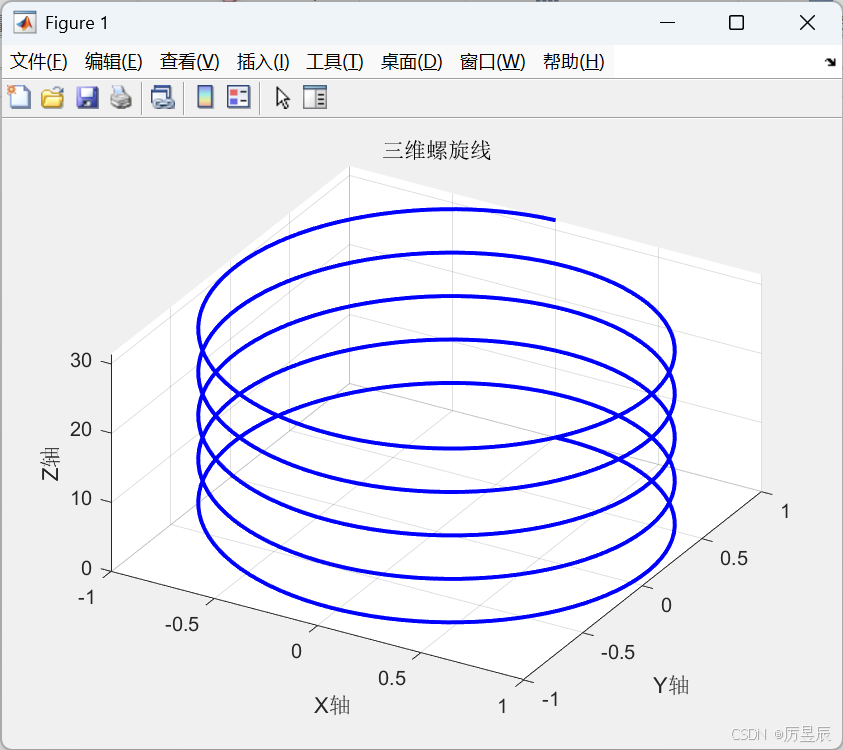

2.2 三维散点图（scatter3）

当需要可视化三维空间中的离散数据点时，scatter3是最佳选择。

% 生成随机三维散点数据
rng(42); % 设置随机种子保证可重复性
n = 300;
x = randn(n, 1);
y = randn(n, 1);
z = randn(n, 1);
c = sin(x) + cos(y) + tan(z); % 颜色数据% 绘制三维散点图
figure;
scatter3(x, y, z, 40, c, 'filled');
colormap('jet'); % 设置颜色映射
colorbar; % 添加颜色条
xlabel('X');
ylabel('Y');
zlabel('Z');
title('三维散点图（颜色表示函数值）');
view(-30, 25);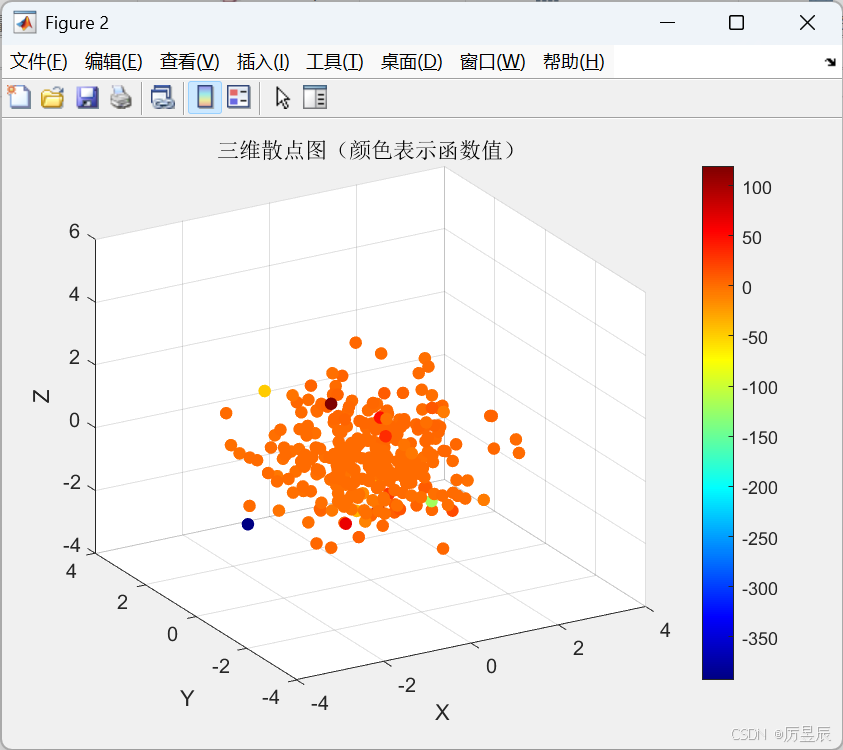

2.3 三维网格图（mesh）

网格图适用于可视化函数z=f(x,y)的曲面。

% 创建网格数据
[X, Y] = meshgrid(-3:0.1:3, -3:0.1:3);
Z = sin(X) .* cos(Y) .* exp(-(X.^2 + Y.^2)/5);% 绘制三维网格图
figure;
mesh(X, Y, Z);
xlabel('X');
ylabel('Y');
zlabel('Z');
title('函数 z = sin(x)cos(y)e^{-(x^2+y^2)/5} 的网格图');
colormap('cool');
colorbar;
view(40, 30);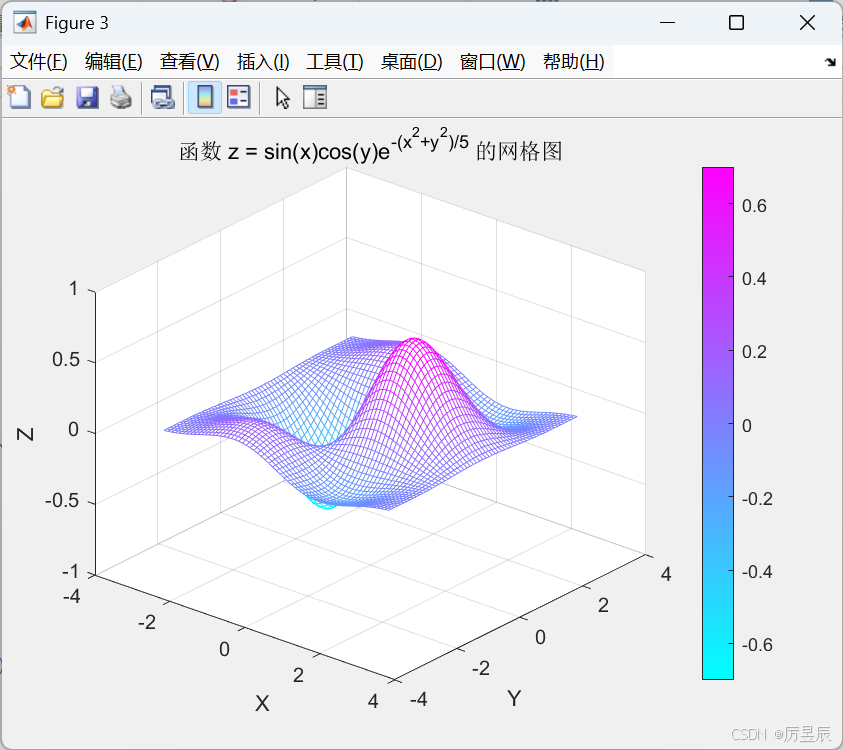

2.4 三维曲面图（surf）

曲面图与网格图类似，但表面被颜色填充，更易观察曲面特征。

% 创建曲面数据
[X, Y] = meshgrid(-2:0.1:2);
Z = X.*exp(-X.^2 - Y.^2);% 绘制三维曲面图
figure;
surf(X, Y, Z, 'EdgeColor', 'none'); % 移除网格线
shading interp; % 平滑着色
xlabel('X');
ylabel('Y');
zlabel('Z');
title('函数 z = x e^{-x^2-y^2} 的曲面图');
colormap('turbo');
colorbar;
light; % 添加光源
lighting gouraud; % 设置光照模式
material shiny; % 设置材质属性
view(-30, 50);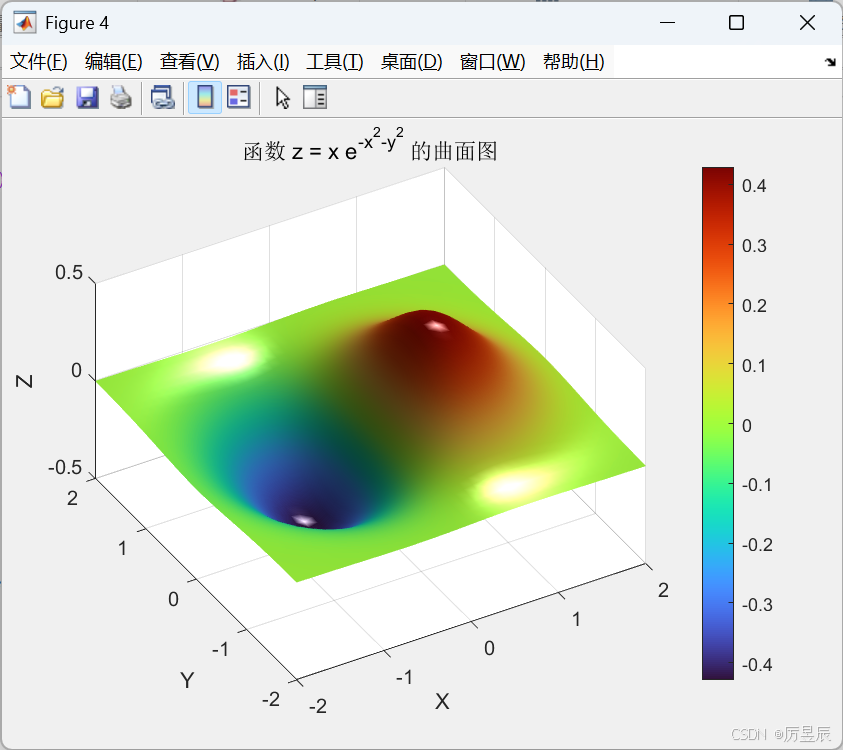

3. 参数曲面绘制

参数曲面通过参数方程定义，常用于绘制复杂几何形状。

% 绘制环面（torus）
theta = linspace(0, 2*pi, 50);
phi = linspace(0, 2*pi, 50);
[Theta, Phi] = meshgrid(theta, phi);R = 2; % 大半径
r = 0.5; % 小半径% 参数方程
x = (R + r*cos(Theta)) .* cos(Phi);
y = (R + r*cos(Theta)) .* sin(Phi);
z = r * sin(Theta);% 绘制环面
figure;
surf(x, y, z);
axis equal;
xlabel('X');
ylabel('Y');
zlabel('Z');
title('环面（Torus）');
colormap('parula');
shading interp;
light;
lighting gouraud;
view(30, 25);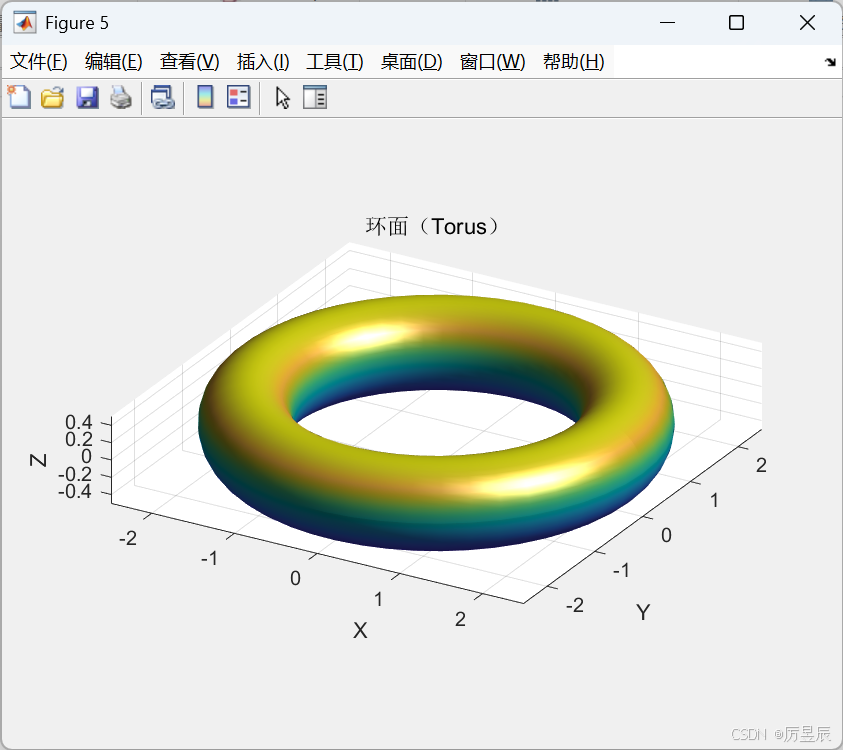

4. 三维等值面可视化

等值面是三维标量场中值相等的点构成的曲面，在科学可视化中极为重要。

% 创建三维网格
[x, y, z] = meshgrid(-2:0.2:2, -2:0.2:2, -2:0.2:2);% 定义三维函数
f = x.^2 + y.^2 + z.^2;% 绘制等值面
figure;
isovalue = 1.5;
p = patch(isosurface(x, y, z, f, isovalue));
isonormals(x, y, z, f, p);
set(p, 'FaceColor', 'red', 'EdgeColor', 'none');
daspect([1 1 1]); % 设置坐标轴比例
view(3); 
axis tight;
camlight; 
lighting gouraud;
xlabel('X');
ylabel('Y');
zlabel('Z');
title(sprintf('等值面: x^2 + y^2 + z^2 = %.1f', isovalue));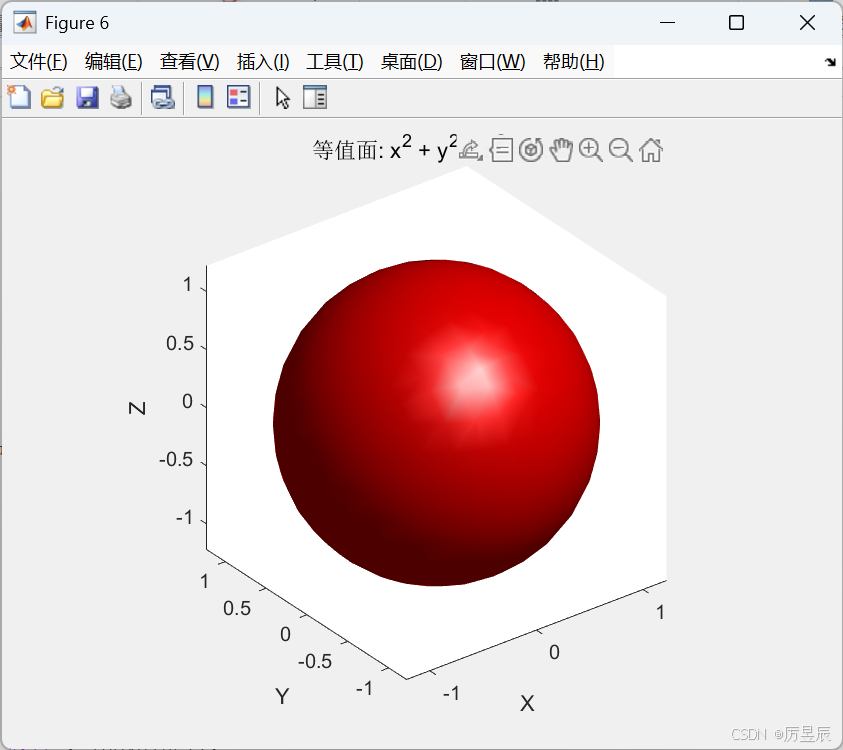

5. 高级三维可视化

5.1 矢量场可视化（quiver3）

quiver3函数用于可视化三维矢量场。

% 创建网格
[X, Y, Z] = meshgrid(-1.5:0.5:1.5);% 定义矢量场
U = Y; % x方向分量
V = -X; % y方向分量
W = Z/2; % z方向分量% 绘制三维矢量场
figure;
quiver3(X, Y, Z, U, V, W, 2, 'LineWidth', 1.5);
xlabel('X');
ylabel('Y');
zlabel('Z');
title('三维矢量场：旋转流');
axis equal;
view(25, 35);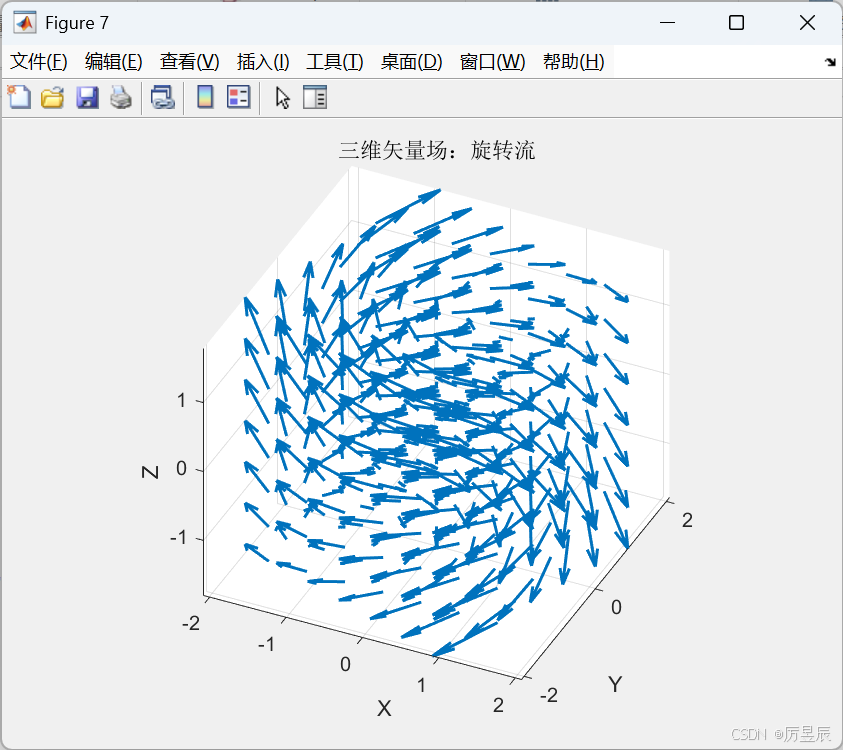

5.2 三维流线图（streamline）

流线图展示矢量场中的流动轨迹。

% 加载MATLAB自带的风场数据
load wind% 确定流线起点
[sx, sy, sz] = meshgrid(80, 20:10:50, 0:5:15);% 绘制三维流线
figure;
streamline(x, y, z, u, v, w, sx, sy, sz);
axis tight;
box on;
view(3);
xlabel('X');
ylabel('Y');
zlabel('Z');
title('三维风场流线图');
colormap('jet');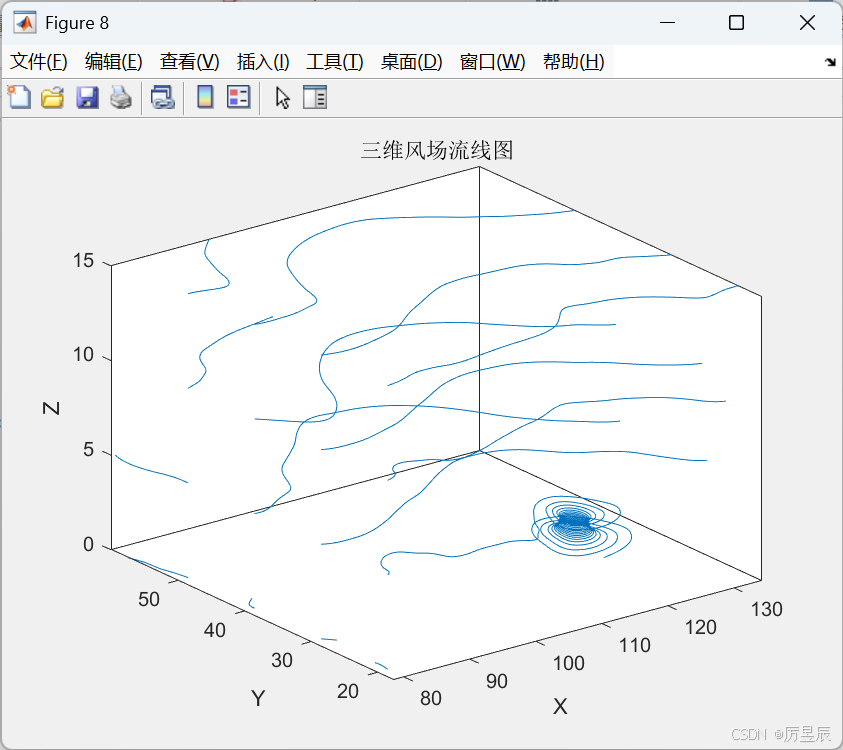

5.3 圆锥体图（coneplot）

圆锥体图以三维圆锥体表示矢量场，更直观展示矢量方向和大小。

% 继续使用风场数据
load wind% 选择圆锥位置
xrange = linspace(min(x(:)), max(x(:)), 6);
yrange = linspace(min(y(:)), max(y(:)), 6);
zrange = linspace(min(z(:)), max(z(:)), 6);
[cx, cy, cz] = meshgrid(xrange, yrange, zrange(1:3));% 绘制圆锥体图
figure;
h = coneplot(x, y, z, u, v, w, cx, cy, cz, 3);
set(h, 'FaceColor', 'red', 'EdgeColor', 'none');
axis tight;
box on;
view(3);
xlabel('X');
ylabel('Y');
zlabel('Z');
title('三维风场圆锥体图');
camlight; 
lighting gouraud;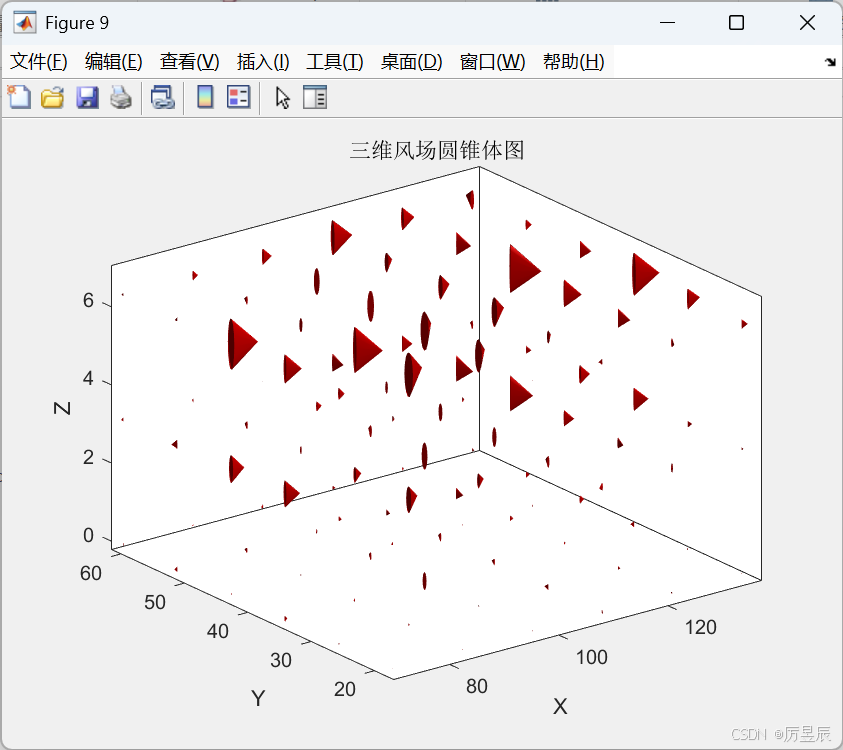

6. 光照与材质处理

光照和材质设置能显著增强三维图形的真实感和可读性。

% 创建一个复杂曲面
[X, Y] = meshgrid(-3:0.1:3);
Z = peaks(X, Y);% 绘制带光照的曲面
figure;
surf(X, Y, Z, 'FaceColor', 'interp', 'EdgeColor', 'none');
colormap('hot');
colorbar;% 设置光照
light1 = light('Position', [-1 -1 1], 'Style', 'infinite');
light2 = light('Position', [1 1 1], 'Style', 'infinite');% 设置材质
material([0.3 0.8 0.2 10 0.5]); % [ambient diffuse specular shine transparency]% 设置视角
view(30, 45);
title('带光照和材质处理的曲面');
xlabel('X');
ylabel('Y');
zlabel('Z');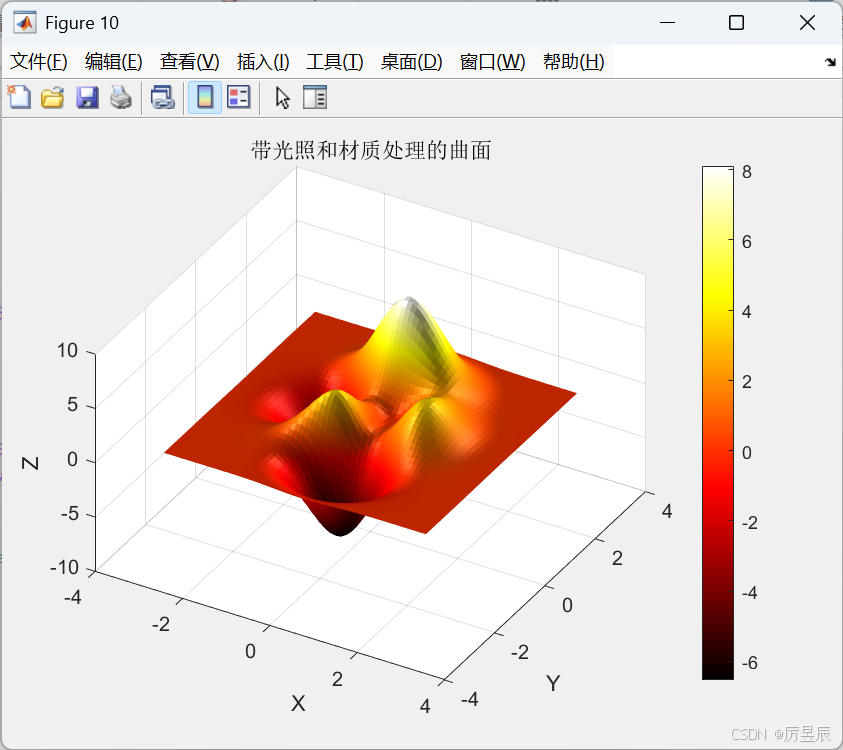

7. 交互式操作与视角控制

MATLAB提供强大的交互功能，让用户能够动态探索三维图形。

% 创建交互式三维图形
[X, Y] = meshgrid(-2:0.1:2);
Z = X.*exp(-X.^2 - Y.^2);figure;
h = surf(X, Y, Z);
shading interp;
colormap('jet');
colorbar;
title('交互式三维曲面');
xlabel('X');
ylabel('Y');
zlabel('Z');% 启用旋转
rotate3d on;% 添加视角控制按钮
uicontrol('Style', 'pushbutton', 'String', 'XY平面',...'Position', [20 20 80 30],...'Callback', 'view(0,90)');uicontrol('Style', 'pushbutton', 'String', 'XZ平面',...'Position', [120 20 80 30],...'Callback', 'view(0,0)');uicontrol('Style', 'pushbutton', 'String', '等轴视图',...'Position', [220 20 80 30],...'Callback', 'view(3); axis equal');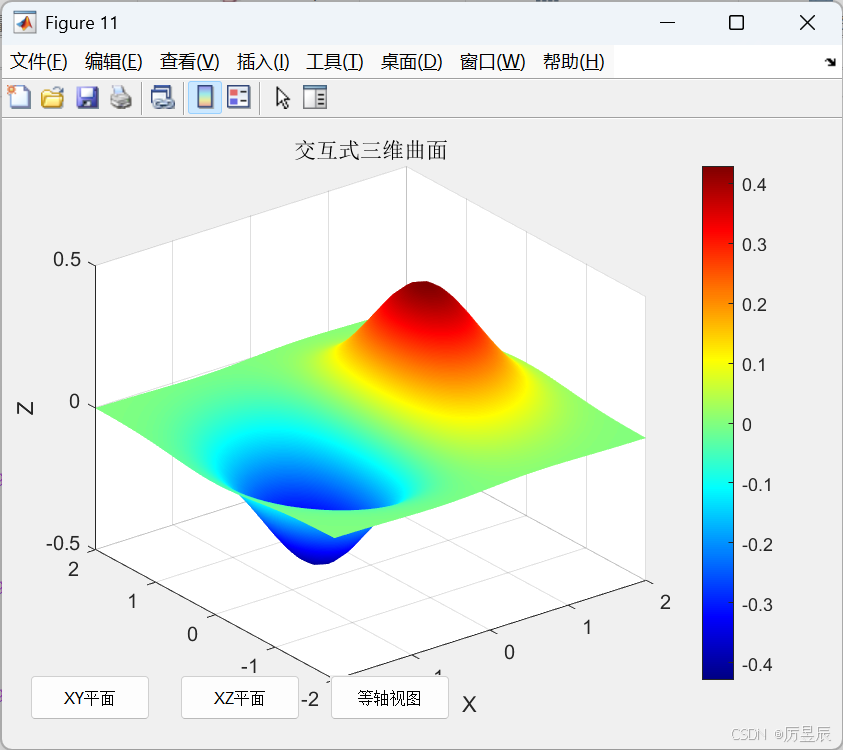

8. 三维可视化应用实例

8.1 分子结构可视化

% 模拟分子结构数据
atoms = {'C', [0, 0, 0], 12;   % 碳原子'O', [1.2, 0, 0], 16; % 氧原子'H', [0, 1, 0], 1;    % 氢原子'H', [0, 0, 1], 1;    % 氢原子'H', [0, -1, 0], 1;   % 氢原子
};% 绘制分子结构
figure;
hold on;% 绘制原子
colors = containers.Map({'C', 'O', 'H'}, {[0.5 0.5 0.5], [1 0 0], [0.8 0.8 1]});
sizes = containers.Map({'C', 'O', 'H'}, {40, 35, 20});for i = 1:size(atoms, 1)atom = atoms{i, 1};pos = atoms{i, 2};scatter3(pos(1), pos(2), pos(3), sizes(atom), colors(atom), 'filled');
end% 绘制键
bonds = [1, 2; % C-O1, 3; % C-H1, 4; % C-H1, 5; % C-H
];for i = 1:size(bonds, 1)a1 = atoms{bonds(i, 1), 2};a2 = atoms{bonds(i, 2), 2};plot3([a1(1), a2(1)], [a1(2), a2(2)], [a1(3), a2(3)], 'k-', 'LineWidth', 2);
end% 设置图形属性
title('甲醇分子结构');
axis equal;
grid on;
xlabel('X (Å)');
ylabel('Y (Å)');
zlabel('Z (Å)');
view(40, 25);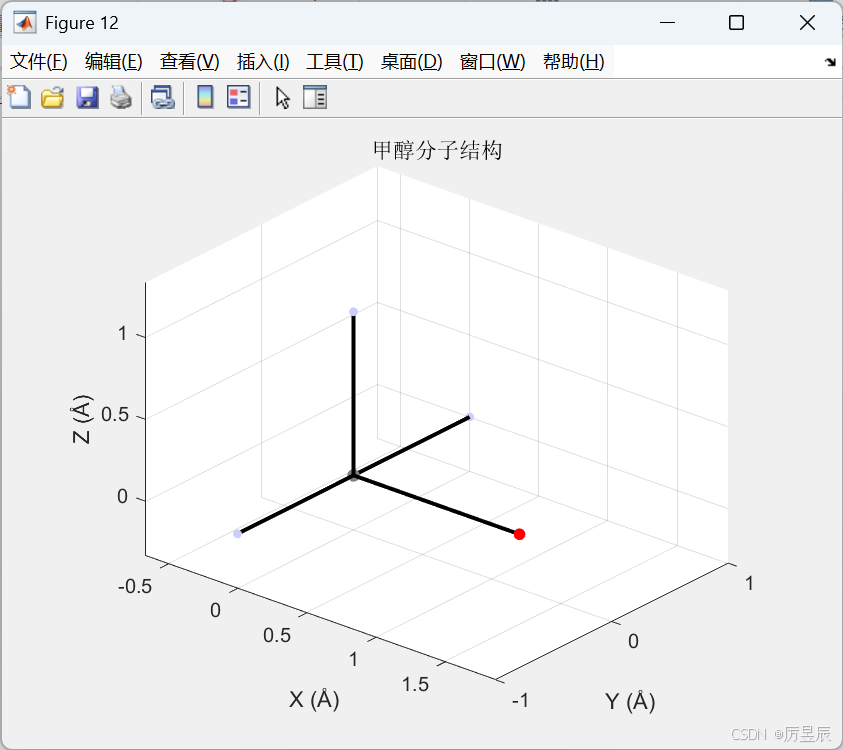

8.2 地形可视化

% 加载地形数据
load topo;% 创建地球表面
figure;
[x, y, z] = sphere(50);
h = surf(x, y, z, 'FaceColor', 'texturemap', 'CData', topo, 'EdgeColor', 'none');% 设置光照
light('Position', [1 1 1], 'Style', 'infinite');
lighting gouraud;
material dull;% 设置标题和坐标轴
title('地球地形图');
axis equal off;
rotate3d on;% 添加经纬度网格
hold on;
[lat, lon] = meshgrid(-90:30:90, -180:30:180);
[lat, lon, alt] = geodetic2ecef(lat, lon, zeros(size(lat)));
plot3(lat, lon, alt, 'k.', 'MarkerSize', 4);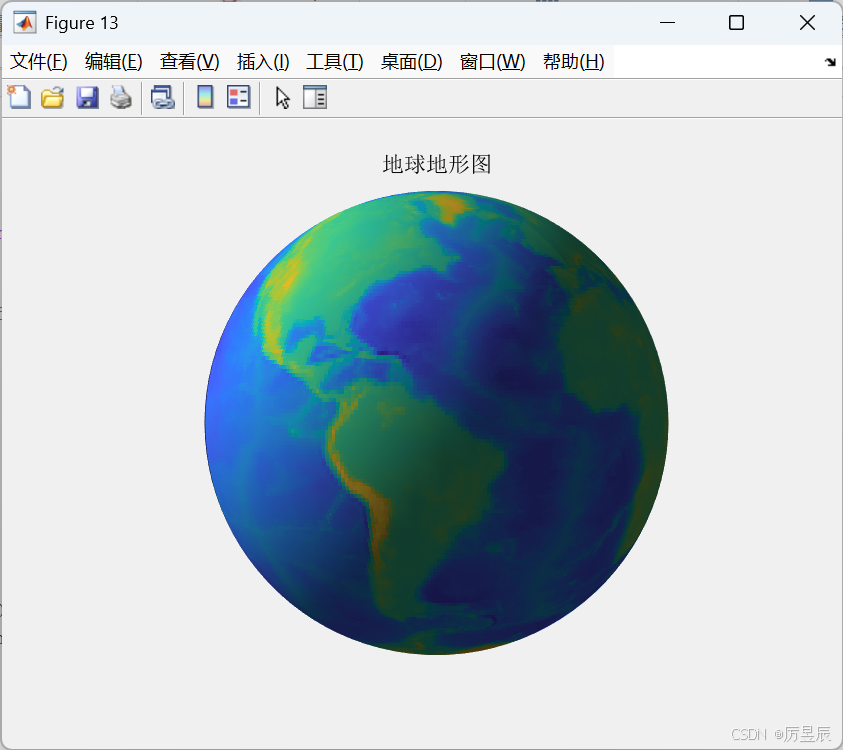

9. 结语

MATLAB提供了丰富而强大的三维可视化工具集，从基本的曲线、曲面绘制到高级的等值面、矢量场可视化，再到交互式操作和光照效果处理，能够满足科研和工程中的各种可视化需求。通过本文介绍的技巧和方法，您可以：

  1. 创建高质量的三维科学图表

  2. 直观展示复杂数据集的空间结构

  3. 动态探索三维模型的不同视角

  4. 增强图形的视觉表现力和信息传达效率

掌握MATLAB的三维可视化技能，将极大地提升您的数据分析和结果展示能力。建议读者在实际应用中多尝试不同的函数参数和组合，探索MATLAB三维可视化的更多可能性。

http://www.lryc.cn/news/620758.html

相关文章：

  • OpenCV Canny 边缘检测
  • 【js】让项目支持倾听和朗读AI技术
  • OpenCV图像平滑处理方法详解
  • tp5集成elasticsearch笔记
  • 开疆智能Ethernet转ModbusTCP网关连接UR机器人配置案例
  • ComfyUI工作流不动了？
  • OpenCV 形态学操作
  • Spring AI PagePdfDocumentReader 全解析：基于 Apache PdfBox 的按页 PDF 读取实战
  • COLMAP进行密集重建，三维重建的步骤
  • [机器学习]08-基于逻辑回归模型的鸢尾花数据集分类
  • AUTOSAR汽车电子嵌入式编程精讲300篇-【自动驾驶】硬件在环（HIL）（二）
  • 第四天～在CANFD或CAN2.0的ARXML文件中实现Multiplexor多路复用信号实战
  • 依托AR远程协助，沟通协作，高效流畅
  • 读From GPT-2 to gpt-oss: Analyzing the Architectural Advances
  • 第四天-创建一个Classic CAN（经典CAN2.0）/CANFD的系统描述ARXML文件
  • IDEA、Pycharm、DataGrip等激活破解冲突问题解决方案之一
  • 学习设计模式《二十二》——职责链模式
  • 深入了解linux系统—— 线程概念
  • 深入解析 Spring IOC 容器在 Web 环境中的启动机制
  • 嵌入式学习Day27
  • stm32项目（29）——基于stm32的智能眼镜设计
  • 【代码随想录day 20】 力扣 108.将有序数组转换为二叉搜索树
  • SwiftUI 页面弹窗操作
  • Linux网络编程：应用层自定义协议与序列化
  • Flutter sqflite插件
  • 支付域——账户系统设计
  • 支持pcm语音文件缓存顺序播放
  • 解剖HashMap的put ＜四＞ jdk1.8
  • OpenCv（二）——边界填充、阈值处理
  • Nacos 配置热更新：Spring Boot Bean 自动获取最新配置