LeetCode 刷题【41. 缺失的第一个正数】

41. 缺失的第一个正数

自己做

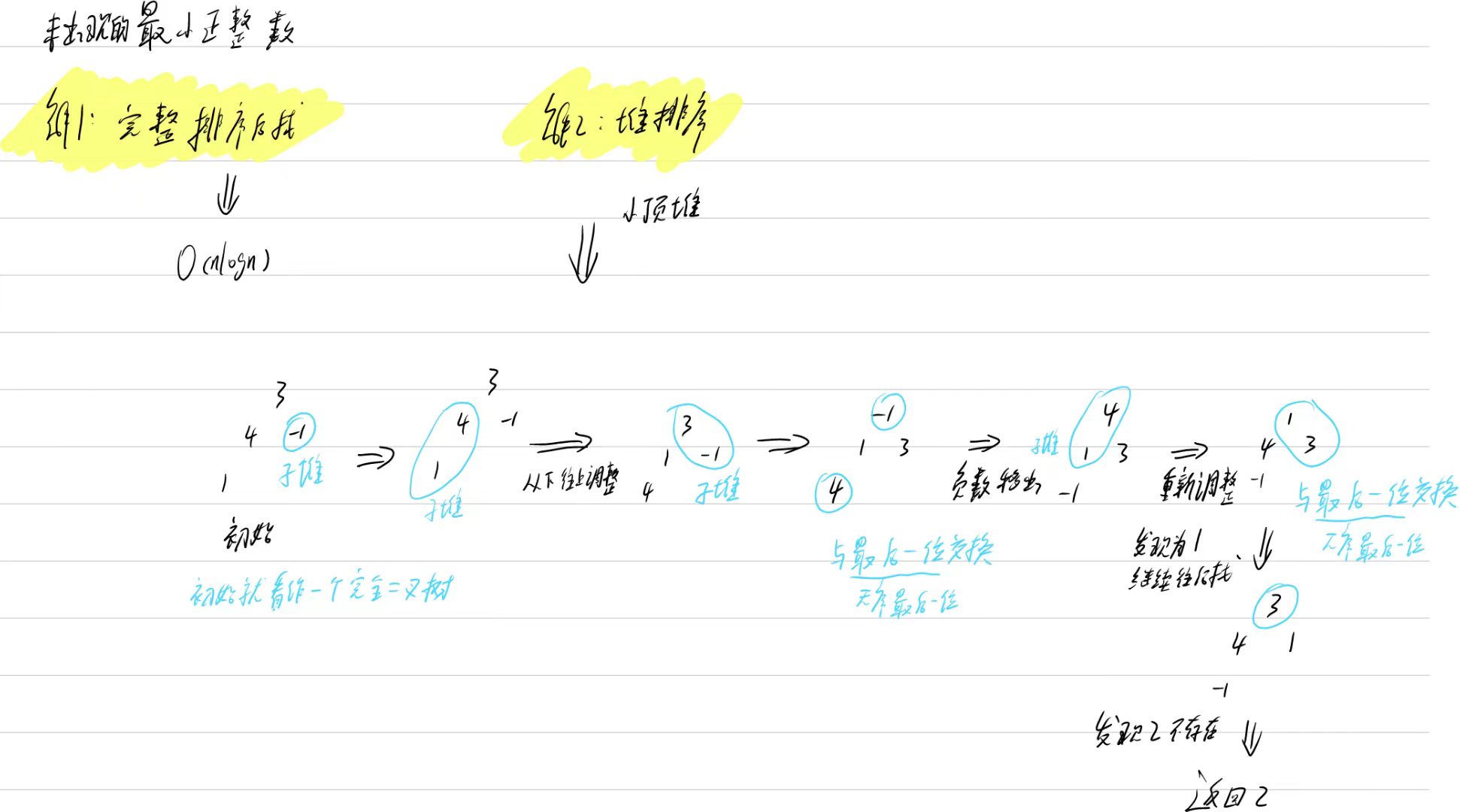
解1：完整排序

class Solution {
public:int firstMissingPositive(vector<int>& nums) {//排序sort(nums.begin(),nums.end());//找数int res = 1;for(int i = 0; i < nums.size(); i++){if(nums[i] > 0 && nums[i] == res)             //nums[i] == res表示该数存在res++;}return res;}
};

解2：堆排序

这里堆排序的代码实现忘了，边搜边做

class Solution {
public://堆排序//调整堆void Heapify(vector<int>& nums, int n, int idx) {          //n表示未排好序的部分【每出堆一个就表示排好一个元素，idx表示堆顶元素的索引下标】int min = idx;        //堆顶元素int left = 2 * idx + 1;    //左下元素int right = 2 * idx + 2;  //右下元素if (left < n && nums[left] < nums[min])     //left < n表示下标在合理范围， nums[left] < nums[min]表示左下更小min = left;if (right < n && nums[right] < nums[min])     //left < n表示下标在合理范围， nums[left] < nums[min]表示左下更小min = right;if (min != idx) {                           //如果发现了比堆顶更小的元素，将堆顶与其交换swap(nums[min], nums[idx]);Heapify(nums, n, min);        //nums[min]与nums[idx]交换后，对于min作为堆顶的子堆中可能会发生变化【比如调整后，其子堆就不是一个合规的子堆了，这就要继续调整】}}//弹出堆顶元素void heapSort(vector<int>& nums, int& res) {int n = nums.size();for (int i = n / 2; i >= 0; i--) {       //从最下面的堆开始调整（右下角最后一个子堆）Heapify(nums, n, i);}//弹出元素【小顶堆中每次调整后，最小元素会出现在索引为0的位置】for (int i = n - 1; i >= 0; i--) {if (nums[0] == res) {            //检查当前最小元素，如果相等则说明这个最小正数已经出现，res++并且继续往后找res++;swap(nums[0], nums[i]);Heapify(nums, i, 0);            //弹出元素后堆又乱了，重新调整}else if (nums[0] < res) {       //nums[0] < res表示现在还没有找到，继续找swap(nums[0], nums[i]);Heapify(nums, i, 0);            //弹出元素后堆又乱了，重新调整}else                        //nums[0] > res说明已经找完了，当前的res就是我们要的结果break;}}int firstMissingPositive(vector<int>& nums) {int res = 1;heapSort(nums, res);return res;}
};

看题解

解：哈希表

根据思路写

class Solution {
public:int firstMissingPositive(vector<int>& nums) {int n = nums.size();vector<bool> hash(n,false);       //哈希表for(int i = 0; i < n; i++){if(nums[i] > 0 && nums[i] <= n){  //在合理范围内就标记已存在hash[nums[i] - 1] = true;}}for(int i = 0; i < n; i++){if(hash[i] == false)return i + 1;}//如果上面全部找不到，说明这是按顺序存放的（从1到n），那么未出现的就是n+1return n + 1;}
};