当前位置：首页 > news >正文

《算法导论》第 23 章 - 最小生成树

news 2025/8/14 14:44:11

引言

大家好！今天我们来深入学习《算法导论》第 23 章的核心内容 ——最小生成树（Minimum Spanning Tree, MST）。无论是网络设计、路径规划还是数据分析，最小生成树都有着广泛的应用。本文将从基础概念出发，详解两种经典算法（Kruskal 和 Prim），并提供可直接运行的 C++ 代码，帮你快速掌握这一重要知识点。

23.1 最小生成树的形成

核心概念

要理解最小生成树的形成，我们需要先掌握几个关键术语：

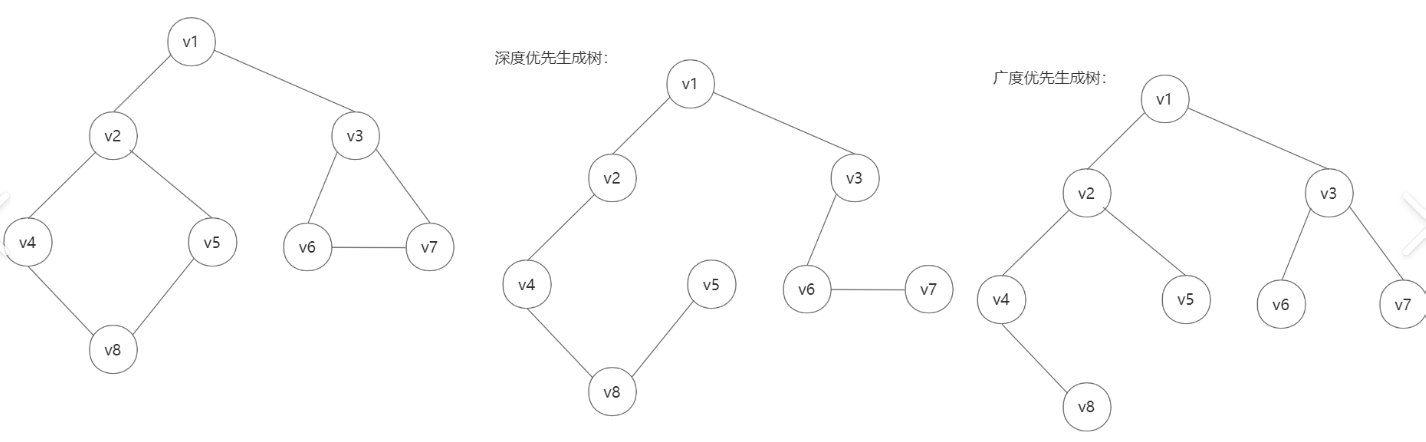
生成树：对于一个包含 n 个顶点的连通图，生成树是一个包含所有 n 个顶点且恰好有 n-1 条边的子图，且子图中无环（否则边数会超过 n-1）。
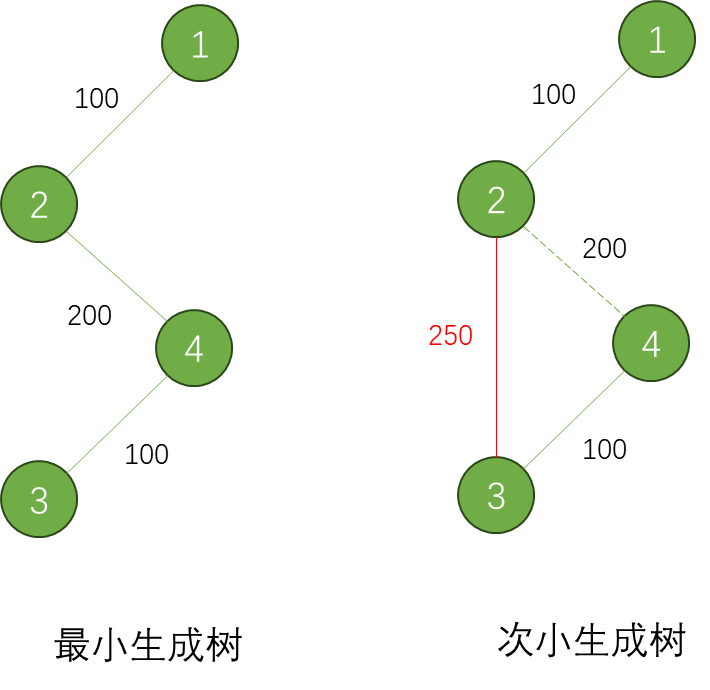
最小生成树：在所有可能的生成树中，边的权重之和最小的生成树。

割与安全边

最小生成树的形成依赖于割（Cut） 和安全边（Safe Edge） 的概念：

割：将图的顶点集划分为两个非空子集的划分方式。例如，将顶点集 V 分为 S 和 V-S（S 是 V 的子集且非空），这就是一个割。
跨边（Cross Edge）：连接割中两个子集（即一个端点在 S，另一个在 V-S）的边。
轻量级跨边（Light Edge）：在一个割的所有跨边中，权重最小的边。
安全边：若一条边加入当前生成树子集中后，不会形成环，且最终能构成最小生成树，则这条边是安全边。

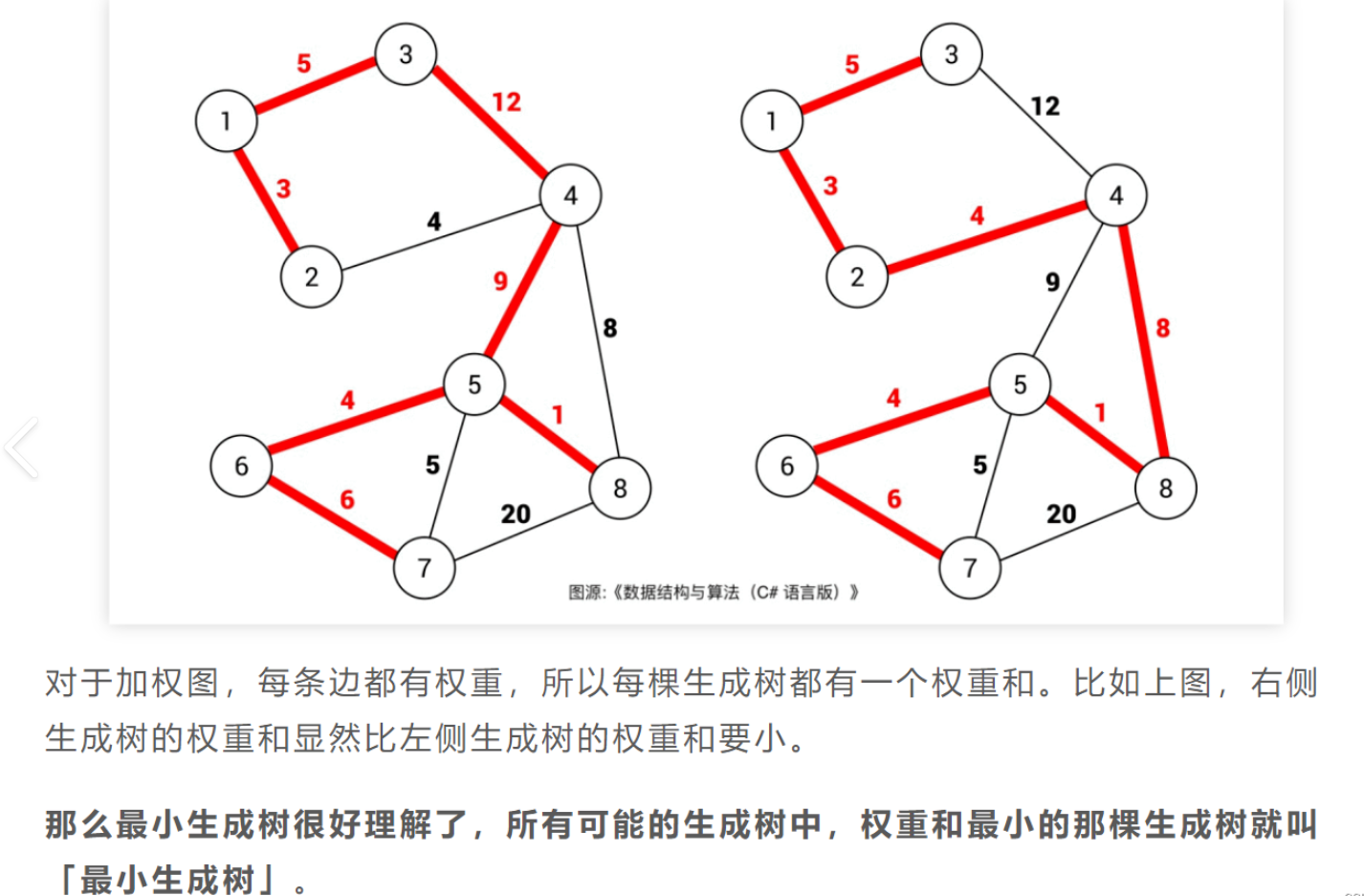
核心定理：对于任意一个割，若该割不包含生成树中的边，则该割的轻量级跨边是安全边。

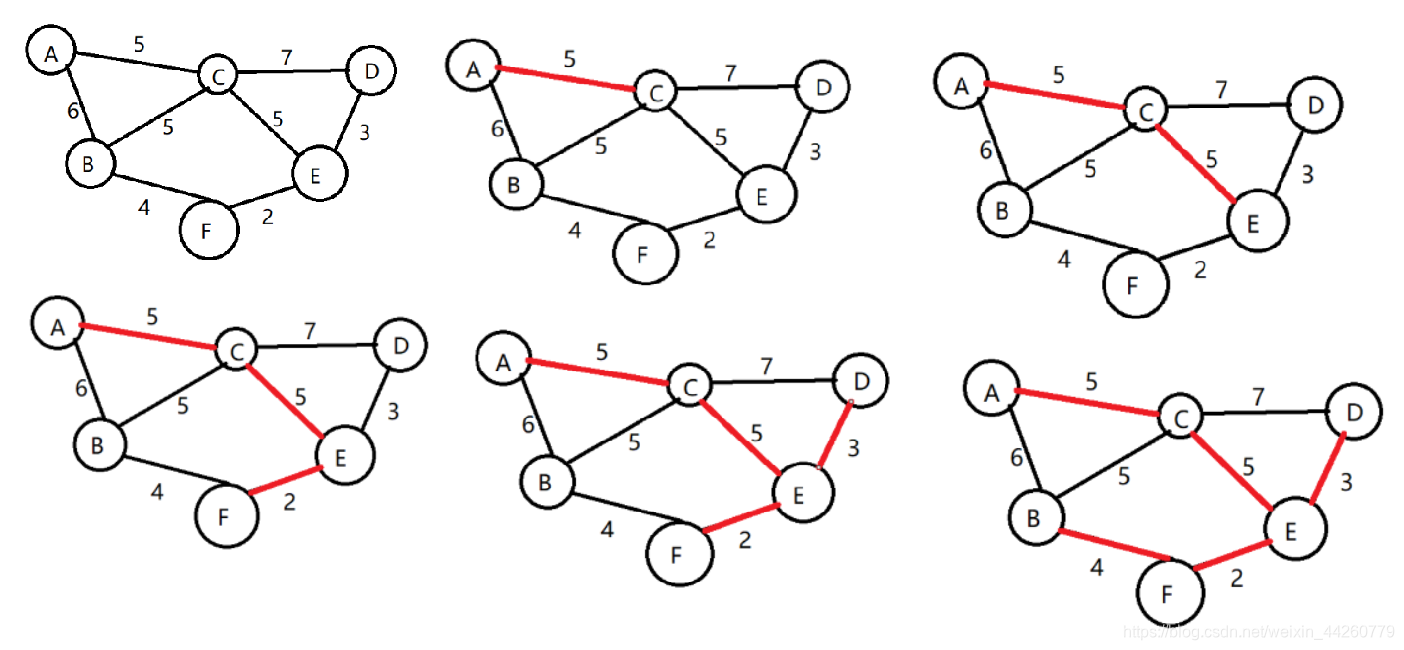
这个定理是 Kruskal 和 Prim 算法的核心理论基础 —— 通过不断选择安全边，最终形成最小生成树。

23.2 Kruskal 算法和 Prim 算法

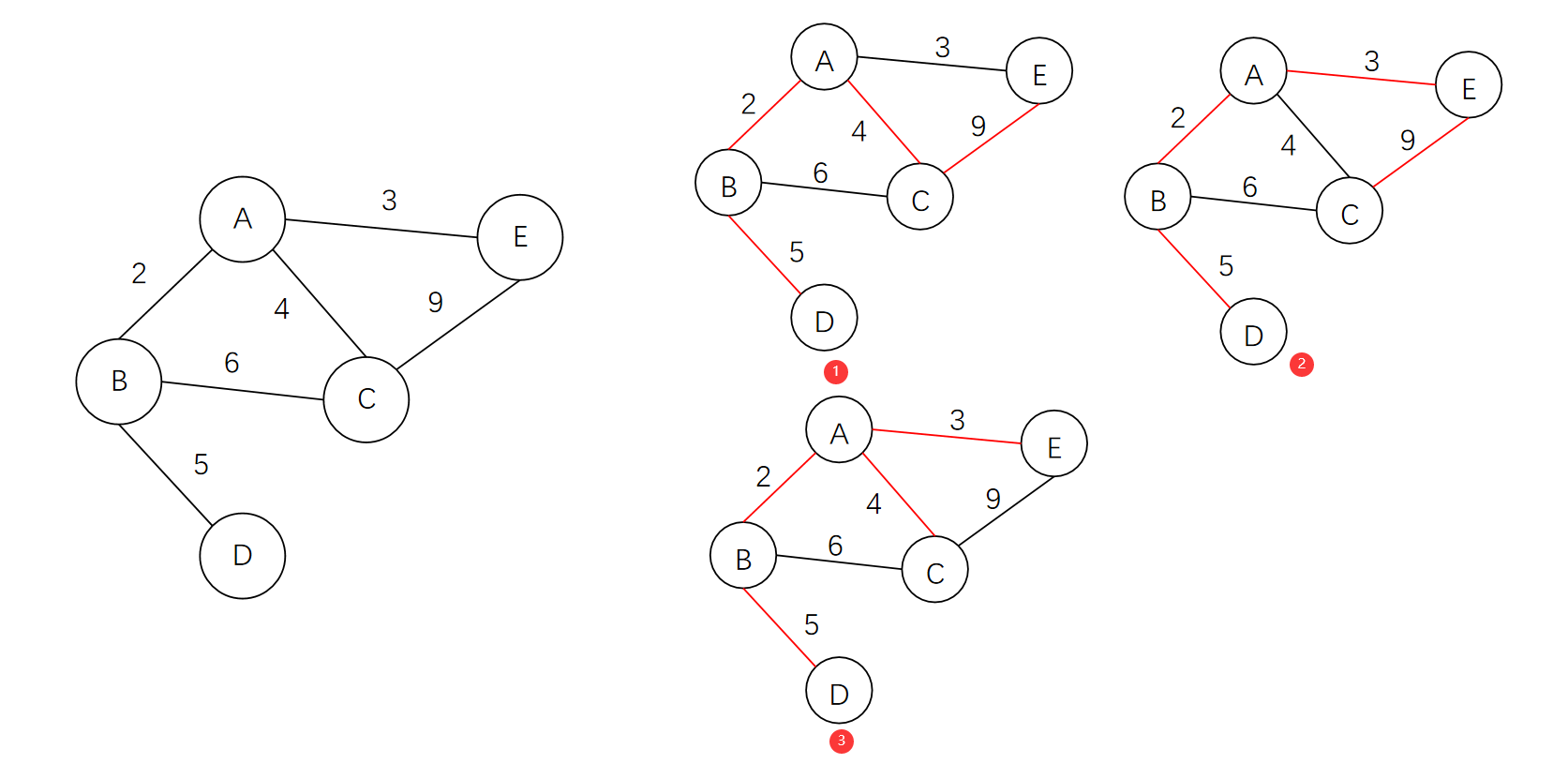
1. Kruskal 算法

算法思想

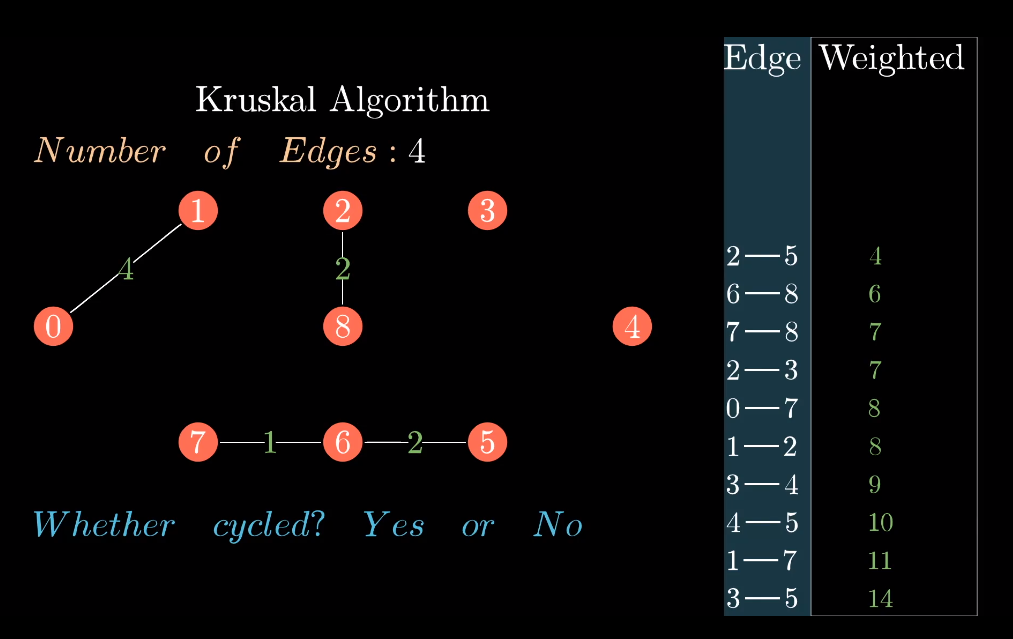
Kruskal 算法的核心是 **“选边避环”**：先将所有边按权重从小到大排序，然后依次选择边加入生成树，若加入的边会形成环则跳过，直到选够 n-1 条边（n 为顶点数）。

代码实现（C++）

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;// 边的结构体：起点、终点、权重
struct Edge {int u, v, weight;Edge(int u_, int v_, int w_) : u(u_), v(v_), weight(w_) {}
};// 并查集（Union-Find）数据结构，用于检测环
class UnionFind {
private:vector<int> parent; // 父节点数组vector<int> rank;   // 秩（用于路径压缩优化）
public:// 初始化：每个节点的父节点是自己，秩为0UnionFind(int n) {parent.resize(n);rank.resize(n, 0);for (int i = 0; i < n; ++i)parent[i] = i;}// 查找根节点（带路径压缩）int find(int x) {if (parent[x] != x)parent[x] = find(parent[x]); // 路径压缩：直接指向根节点return parent[x];}// 合并两个集合（按秩合并）void unite(int x, int y) {x = find(x);y = find(y);if (x == y) return; // 已在同一集合// 秩小的树合并到秩大的树if (rank[x] < rank[y])parent[x] = y;else {parent[y] = x;if (rank[x] == rank[y])rank[x]++;}}
};// Kruskal算法实现
void kruskal(int n, vector<Edge>& edges) {// 按权重从小到大排序边sort(edges.begin(), edges.end(), [](const Edge& a, const Edge& b) {return a.weight < b.weight;});UnionFind uf(n);vector<Edge> mst; // 存储最小生成树的边int totalWeight = 0;for (const Edge& e : edges) {// 若u和v不在同一集合，加入边并合并集合if (uf.find(e.u) != uf.find(e.v)) {mst.push_back(e);totalWeight += e.weight;uf.unite(e.u, e.v);// 生成树有n-1条边时停止if (mst.size() == n - 1)break;}}// 输出结果cout << "Kruskal算法生成的最小生成树边：" << endl;for (const Edge& e : mst) {cout << "(" << e.u << ", " << e.v << ") 权重：" << e.weight << endl;}cout << "总权重：" << totalWeight << endl;
}// 测试案例
int main() {/* 测试图（顶点0-4）：0-1(2), 0-3(6)1-2(3), 1-3(8), 1-4(5)2-4(7)3-4(9)*/int n = 5; // 5个顶点vector<Edge> edges;edges.emplace_back(0, 1, 2);edges.emplace_back(0, 3, 6);edges.emplace_back(1, 2, 3);edges.emplace_back(1, 3, 8);edges.emplace_back(1, 4, 5);edges.emplace_back(2, 4, 7);edges.emplace_back(3, 4, 9);kruskal(n, edges);return 0;
}

代码说明

并查集：核心作用是高效检测环（find操作）和合并集合（unite操作），通过路径压缩和按秩合并优化，时间复杂度接近 O (1)。
排序边：Kruskal 算法的时间瓶颈在排序，因此总复杂度为 O (E log E)（E 为边数）。
适用场景：稀疏图（边数少），因为排序边的成本较低。

2. Prim 算法

算法思想

Prim 算法的核心是 **“从顶点扩展”**：从任意顶点开始，逐步将顶点加入生成树，每次选择连接 “已加入集合” 和 “未加入集合” 的权重最小的边，直到所有顶点都加入。

代码实现（C++，邻接矩阵版）

#include <iostream>
#include <vector>
#include <climits> // 用于INT_MAX
using namespace std;// Prim算法（邻接矩阵实现，适合稠密图）
void prim(int n, const vector<vector<int>>& graph) {vector<int> key(n, INT_MAX);   // 顶点到生成树的最小边权重vector<int> parent(n, -1);     // 父节点数组vector<bool> inMST(n, false);  // 标记是否在生成树中int totalWeight = 0;           // 声明总权重变量（修复作用域问题）key[0] = 0; // 从顶点0开始，初始权重为0for (int count = 0; count < n; ++count) { // 迭代n次（加入所有顶点）// 步骤1：选key最小且不在MST中的顶点uint u = -1;for (int v = 0; v < n; ++v) {if (!inMST[v] && (u == -1 || key[v] < key[u]))u = v;}inMST[u] = true; // 将u加入生成树if (parent[u] != -1) // 累加权重（跳过起始顶点）totalWeight += graph[u][parent[u]];// 步骤2：更新u的邻接顶点的key值for (int v = 0; v < n; ++v) {// 若v不在MST，且存在边(u,v)，且权重小于当前key[v]if (graph[u][v] != 0 && !inMST[v] && graph[u][v] < key[v]) {key[v] = graph[u][v];parent[v] = u;}}}// 输出结果cout << "Prim算法生成的最小生成树边：" << endl;for (int i = 1; i < n; ++i) { // 从1开始（跳过起始顶点0）cout << "(" << parent[i] << ", " << i << ") 权重：" << graph[i][parent[i]] << endl;}cout << "总权重：" << totalWeight << endl;
}// 测试案例
int main() {/* 测试图（顶点0-4，邻接矩阵表示，0表示无直接边）：0: [0, 2, 0, 6, 0]1: [2, 0, 3, 8, 5]2: [0, 3, 0, 0, 7]3: [6, 8, 0, 0, 9]4: [0, 5, 7, 9, 0]*/int n = 5;vector<vector<int>> graph = {{0, 2, 0, 6, 0},{2, 0, 3, 8, 5},{0, 3, 0, 0, 7},{6, 8, 0, 0, 9},{0, 5, 7, 9, 0}};prim(n, graph);return 0;
}

代码说明

邻接矩阵：适合稠密图（边数多），时间复杂度为 O (V²)（V 为顶点数）。
优先队列优化版：若用优先队列（最小堆）存储顶点的 key 值，时间复杂度可优化为 O (E log V)，适合稀疏图（需用邻接表存储图）。
适用场景：稠密图（顶点数少、边数多），因为 O (V²) 在 V 小时效率高于 Kruskal 的 O (E log E)。

综合案例：城市光缆铺设

问题描述

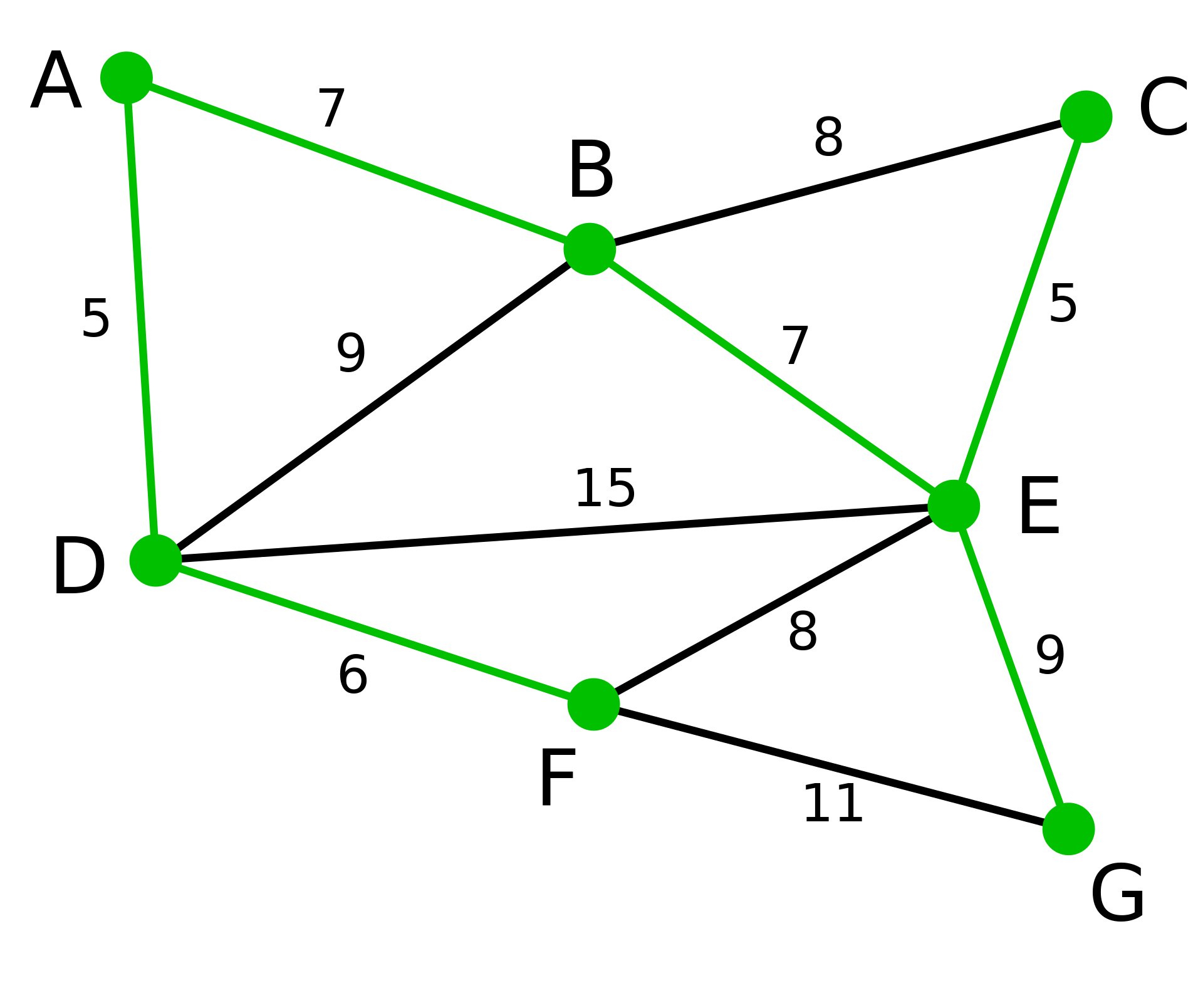
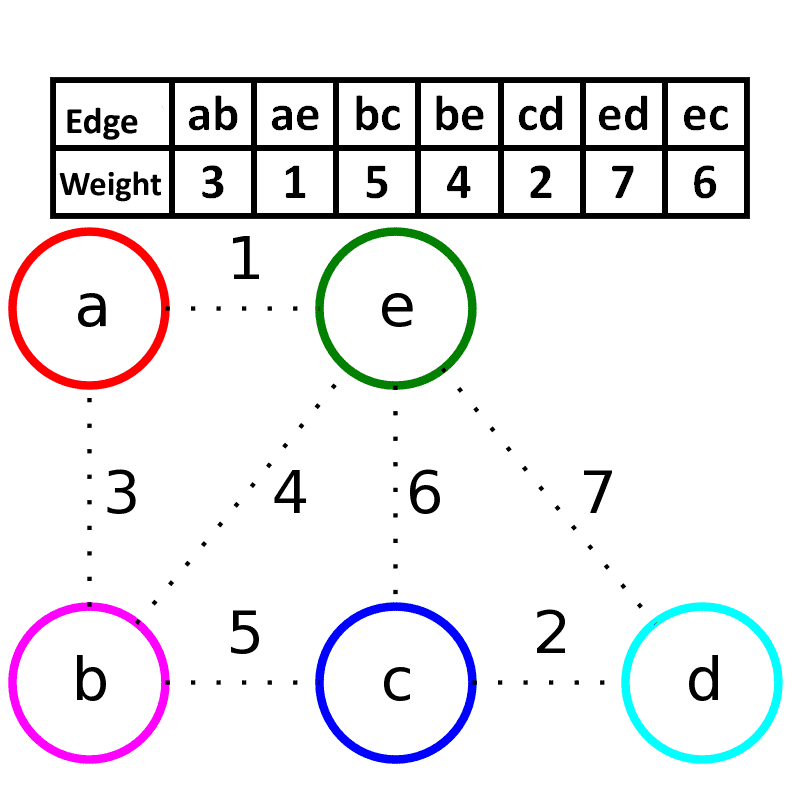
假设有 5 个城市（编号 0-4），需要铺设光缆连接所有城市，各城市间的光缆成本如下表。求最小总成本的铺设方案。

城市对	(0,1)	(0,3)	(1,2)	(1,3)	(1,4)	(2,4)	(3,4)
成本	2	6	3	8	5	7	9

解决方案

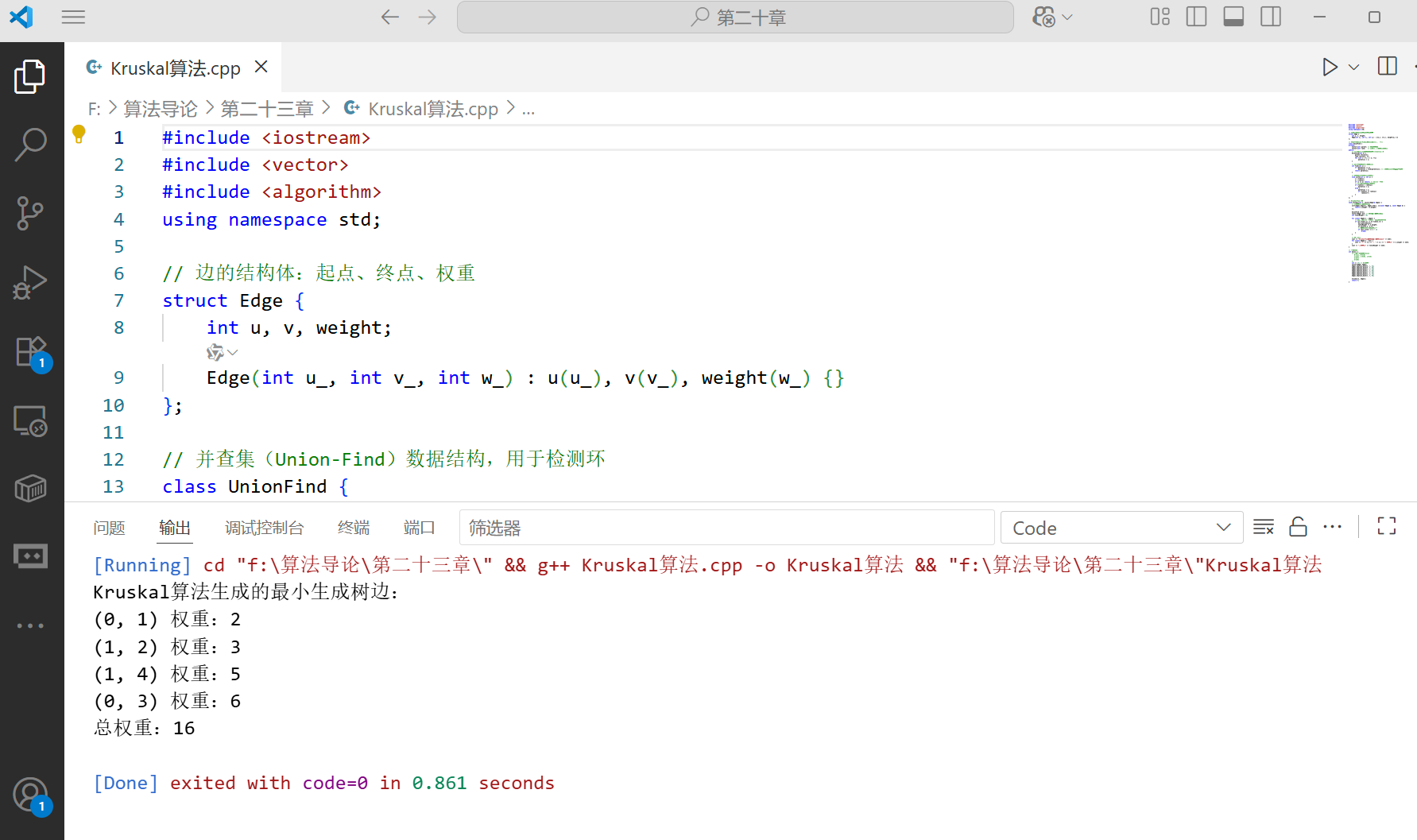
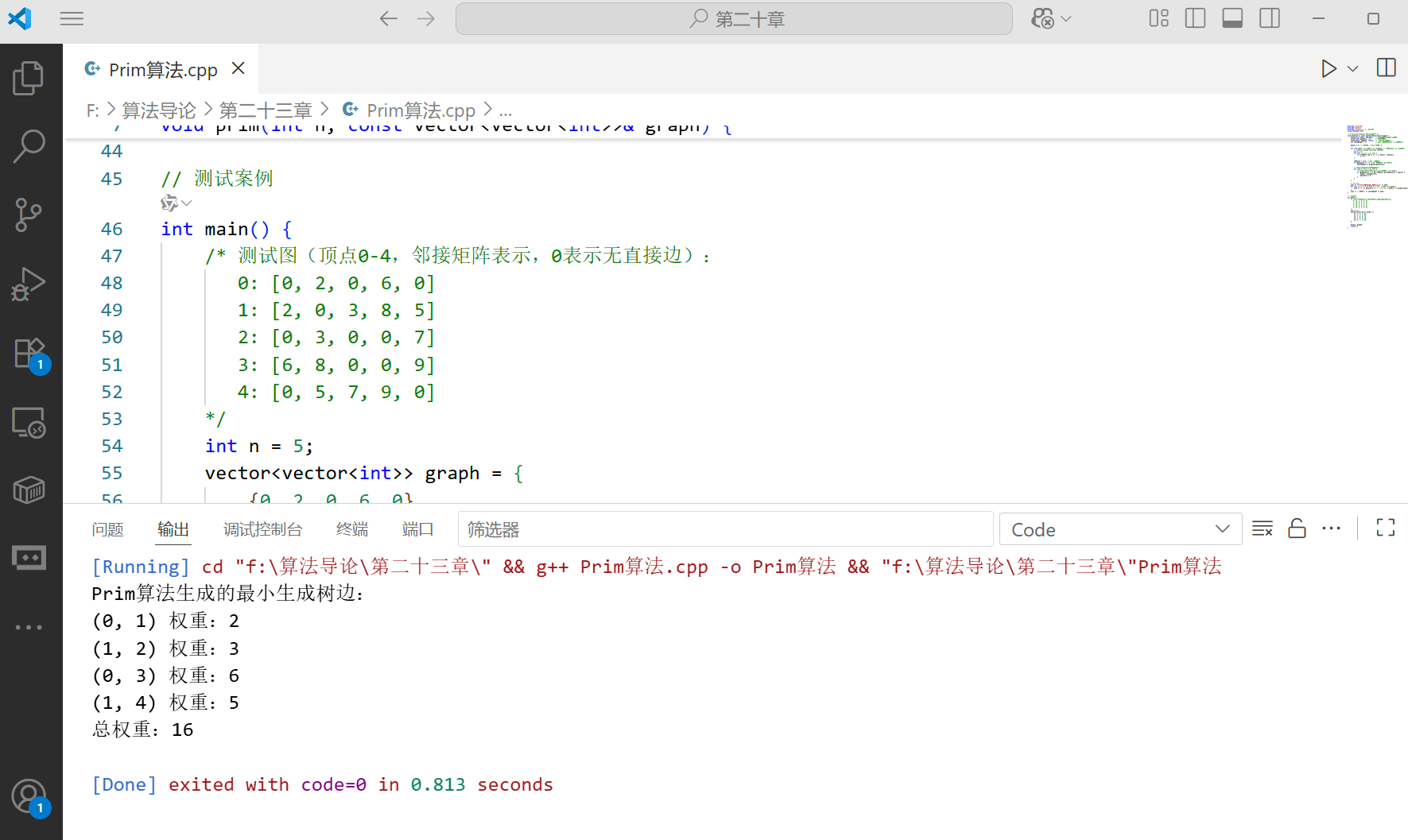
分别用 Kruskal 和 Prim 算法求解，代码已在上面给出，运行结果如下：

最小总成本：2+3+5+6=16（Kruskal）或相同结果（Prim）
铺设方案：(0,1)、(1,2)、(1,4)、(0,3)

思考题

次小生成树：如何求与最小生成树权重最接近的生成树？（提示：在 MST 中替换一条边为非 MST 边，找权重差最小的方案）
动态 MST：若图中某条边的权重发生变化，如何高效更新 MST？（提示：判断变化的边是否在 MST 中，再针对性调整）
非连通图：若图不连通，如何求 “最小生成森林”（每个连通分量的 MST 集合）？（提示：对每个连通分量分别跑 MST 算法）

本章注记

Kruskal 算法由 Joseph Kruskal 于 1956 年提出，Prim 算法由 Robert Prim 于 1957 年提出，两者均基于 “贪心思想”（每次选局部最优）。
另一种经典的 MST 算法是 Boruvka 算法（1926 年），时间复杂度为 O (E log V)，适合并行计算。
实际应用中，需根据图的稀疏程度选择算法：稠密图用 Prim（邻接矩阵版），稀疏图用 Kruskal 或 Prim（优先队列版）。