数据结构:队列(Queue)与循环队列(Circular Queue)
目录
理解核心需求——什么是队列?
最直观的实现方式——用数组试试?
操作入队操作 (Enqueue):
模拟出队操作 (Dequeue):
发现重大缺陷!
改进出队操作
发现新缺陷!
最终方案——循环队列
发现最后一个,也是最微妙的缺陷!
解决方案(两种主流方案):
牺牲一个数组单元
最终实现:构建完整的循环队列代码
第 1 步:最终的结构体和创建函数
第 2 步:核心判断逻辑
第 3 步:入队和出队函数
第 4 步:收尾工作(销毁队列)
理解核心需求——什么是队列?
想象一下在食堂排队打饭。每个人都得老老实实地排在队伍的末尾,而食堂师傅每次只给排在队伍最前面的人打饭。
这个生活中的场景,就完美地描述了“队列”的核心思想:
-
先进先出 (First-In, First-Out, FIFO):最早进入队列的元素,也最早离开队列。就像排队,先来的人先打到饭。
-
两个基本操作:
-
入队 (Enqueue):在队伍的末尾(队尾)加入一个新元素。
-
出队 (Dequeue):从队伍的开头(队头)取出一个元素。
-
所以,我们需要设计一个数据结构,它必须高效地支持在“尾部添加”和在“头部移除”这两个操作。

最直观的实现方式——用数组试试?
我们最先想到的、最简单的数据结构就是数组。我们来尝试用数组实现队列。
我们需要两个“指针”(这里先用数组下标代替)来标记队头和队尾。
-
front:指向队头元素。 -
rear:指向下一个可以插入新元素的位置(即队尾元素的下一个位置)。
我们定义一个结构体来表示这个队列:
// 使用C风格的struct,在C和C++中都适用
#define MAX_SIZE 5 // 为了演示,我们先假设队列最多能存5个元素struct ArrayQueue {int data[MAX_SIZE]; // 用数组存储数据int front; // 队头下标int rear; // 队尾下标
};// 初始化
// front=0, rear=-1 表示队列为空。为什么rear是-1?
// 因为这样第一个元素进来后,rear可以先++变成0,再赋值,逻辑比较统一。
// 我们就采用这种 front=0, rear=-1 的约定。操作入队操作 (Enqueue):
假设我们依次入队 11, 22, 33。
假设我们创建一个空队列,front = 0, rear = -1。
初始状态:
Queue: [ , , , , ... ]^front
(rear 在 -1, 看不见)入队 11:
rear 先加 1 变成 0,然后在 data[0] 放入 11。rear 现在指向了队尾元素。
Queue: [ 11, , , , ... ]^front, rear入队 22:
rear 加 1 变成 1,在 data[1] 放入 22。
Queue: [ 11, 22, , , ... ]^ ^front rear入队 33:
rear 加 1 变成 2,在 data[2] 放入 33。
Queue: [ 11, 22, 33, , ... ]^ ^front rear入队逻辑看起来很简单:
q->rear++;
q->data[q->rear] = value;模拟出队操作 (Dequeue):
根据先进先出的原则,队头元素 11 应该先出队。
取出 data[front] 的值后,front 之后的所有元素(22, 33)都必须向前移动一个位置,来填补 11 留下的空位。
出队前:
Queue: [ 11, 22, 33, , ... ]^ ^front rear取出 11 后,我们必须...
将 22 移动到下标 0
将 33 移动到下标 1
更新 rear 到 1出队后:
Queue: [ 22, 33, , , ... ]^ ^front rear发现重大缺陷!
这个出队操作太慢了!如果队列里有 N 个元素,出队一个元素就需要移动 N-1 个元素。
它的时间复杂度是 O(N)。这完全违背了我们希望操作尽可能快(O(1))的初衷。
所以,这个方案因为出队效率低下,被否决。
改进出队操作
我们必须让出队操作也变成 O(1)。怎么做?
核心思路:不出队时移动元素,而是移动
front指针!
让我们重新定义 front 和 rear 的含义,这非常重要:
-
front: 指向队头元素所在的下标。 -
rear: 指向下一个新元素应该被插入位置的下标。
// 还是那个结构体
typedef struct {int data[MAX_SIZE];int front;int rear;
} BetterQueue;// 初始化:
// 让 front 和 rear 都指向 0。
// 约定:当 front == rear 时,队列为空。新约定下的入队和出队
初始状态: front = 0, rear = 0
Queue: [ , , , , ... ]^front, rear入队 11: 在 data[rear] 处放值,然后 rear 后移。data[0]=11; rear=1;
Queue: [ 11, , , , ... ]^ ^front rear入队 22: data[1]=22; rear=2;
Queue: [ 11, 22, , , ... ]^ ^front rear出队: 从 data[front] 取值,然后 front 后移。
value = data[0]; front=1;
Queue: [ 11, 22, , , ... ] //11 所在的位置成了“僵尸数据”,我们不再关心^ ^front rear太棒了!现在入队和出队都只是移动一下下标,时间复杂度都是 O(1)。我们成功了吗?
发现新缺陷!
让我们继续操作。
继续入队: 一直入队,直到 rear 到达数组的末尾 MAX_SIZE。
Queue: [ xx, xx, 33, 44, 55, 66, 77, 88, 99, 100 ]^ ^front rear (rear=10)现在 rear 已经到了数组的尽头,我们无法再入队了。但是!
看数组的前面,front 已经向后移动了,下标 0 和 1 的位置其实是空闲的!
我们遇到了 “假溢出”。数组明明还有空间,但我们却认为它满了。
结论:这个方案虽然高效,但会浪费大量空间,有严重的设计缺陷。
最终方案——循环队列
如何解决“假溢出”?我们需要一种方法能重新利用数组前面被浪费掉的空间。
核心思路:把数组的头和尾“连接”起来,形成一个环。
当 rear 或 front 指针移动到数组末尾时,下一步就让它自动“绕”回数组的开头(下标0)。
这个“绕回”的魔术,用一个简单的数学运算就能实现:取模运算 (%)。
-
front前进一步的公式:front = (front + 1) % MAX_SIZE -
rear前进一步的公式:rear = (rear + 1) % MAX_SIZE
循环的威力
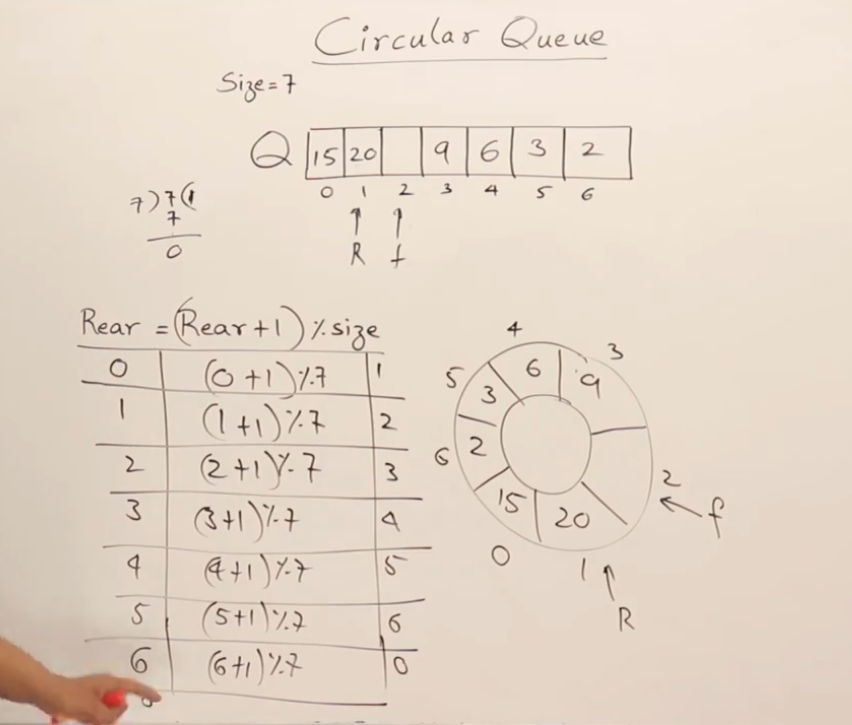
假设 MAX_SIZE 是 5,之前已经出队了两个,又入队了三个,rear 绕回了0
Queue: [ 33, 44, 55, , ]^ ^front(2) rear(0)入队 66: data[rear] = 66; rear = (rear + 1) % 5; => data[0] = 66; rear=1;
Queue: [ 66, 44, 55, , ]^ ^rear front(2)入队 77: data[rear] = 77; rear = (rear + 1) % 5; => data[1] = 77; rear=2;
Queue: [ 66, 77, 55, , ]^rear, front (都等于2)发现最后一个,也是最微妙的缺陷!
看上面的最后一步。我们入队 77 之后,rear 的下标变成了 2,此时 front 的下标也是 2。
front == rear
这和我们最初“队列为空”的约定 front == rear 完全一样了!我们现在无法区分队列是“满”还是“空”。
解决方案(两种主流方案):
-
牺牲一个存储单元:我们规定,当
rear的下一个位置是front时,队列就算满了。这样rear就永远不会真正追上front。-
判满条件:
(rear + 1) % MAX_SIZE == front -
判空条件:
front == rear -
这是最常用、最巧妙的实现方式。
-
-
增加一个计数器:用一个额外的变量
size来记录队列中元素的个数。-
判满条件:
size == MAX_SIZE -
判空条件:
size == 0 -
这种方式很直观,但需要额外维护一个变量。
-
我们采用第一种更经典的方法来构建我们的循环队列。
牺牲一个数组单元
-
重新定义“满” :我们不再认为“所有格子都占满”才叫满。我们换一个定义:
当队列中只剩下最后一个空闲位置时,我们就认为队列已经满了。我们不允许使用这最后一个位置。
这个“牺牲”掉的单元,就是用来区分“满”和“空”的关键。
-
想象“满”的状态
让我们在脑海里(或者纸上)构建这个新的“满”状态。假设
maxSize还是 5。front在下标f的位置。rear指向队尾元素的下一个位置。当队列按照新定义变“满”时,数组里应该有
maxSize - 1个元素,也就是 4 个元素。rear指针应该在哪里?看下图,
front在位置1。我们填入4个元素后,rear最终会停在0的位置。
寻找 front 和 rear 的数学关系
观察上图这个“满”的状态,front 在 1,rear 在 0。它们之间有什么关系?
-
rear好像在front的“前一个”位置。 -
换一种说法:从
rear的位置再向后走一步,就碰到了front。
这个“向后走一步”的操作,在循环队列里如何用数学表达?
-
如果
rear不是在数组末尾,那么就是rear + 1。 -
如果
rear恰好在数组末尾(比如maxSize - 1),下一步就要回到0。
这两个情况可以用一个统一的数学公式来表示:取模运算(Modulo)。 rear 的下一个位置是:(rear + 1) % maxSize
形成判满公式
我们把第2步的观察和第3步的数学表达结合起来。
当队列“满”的时候(按我们的新定义),rear 的下一个位置恰好就是 front 所在的位置。
所以,判满条件就是: rear 的下一个位置 == front
翻译成代码和公式就是:
(rear + 1) % capacity == front
验证这个方案是否解决了矛盾
-
判空条件:我们没有改变它,依然是
front == rear。 -
判满条件:现在是
(rear + 1) % maxSize == front。
在这套新规则下,rear 永远不会追上 front(因为一旦 rear 的下一个位置是 front,就不再允许入队了)。
所以 front == rear 这个状态只可能在一种情况下出现:队列为空。
核心矛盾被完美解决。
这也意味着,一个容量为 k 的队列,其实需要一个大小为 k+1 的数组。
最终实现:构建完整的循环队列代码
现在,我们把所有正确的思想碎片拼接到一起,形成最终的代码。
第 1 步:最终的结构体和创建函数
为了灵活,我们不再用宏定义 MAX_SIZE,而是在创建时动态指定容量。
#include <stdio.h>
#include <stdlib.h> // for malloc and free// 最终版循环队列结构
typedef struct {int* data; // 指向数据数组的指针int capacity; // 数组的总容量 (是我们想存的元素数 k + 1)int front; // 队头指针int rear; // 队尾指针
} CircularQueue;// 创建队列
CircularQueue* createQueue(int k) {CircularQueue* q = (CircularQueue*)malloc(sizeof(CircularQueue));if (!q) return NULL;q->capacity = k + 1; // 牺牲一个单元,所以容量要 k+1q->data = (int*)malloc(q->capacity * sizeof(int));if (!q->data) {free(q);return NULL;}q->front = 0;q->rear = 0;return q;
}
第 2 步:核心判断逻辑
// 判空
int isEmpty(CircularQueue* q) {// 公式: q->front == q->rearreturn q->front == q->rear;
}// 判满
int isFull(CircularQueue* q) {// 公式: (q->rear + 1) % q->capacity == q->frontreturn (q->rear + 1) % q->capacity == q->front;
}第 3 步:入队和出队函数
// 入队
int enqueue(CircularQueue* q, int value) {if (isFull(q)) {printf("Error: 队列已满,无法入队。\n");return 0; // 0 代表失败}q->data[q->rear] = value;q->rear = (q->rear + 1) % q->capacity; // rear 指针使用取模运算前进return 1; // 1 代表成功
}// 出队
int dequeue(CircularQueue* q, int* pValue) { // 用指针传出值if (isEmpty(q)) {printf("Error: 队列为空,无法出队。\n");return 0;}*pValue = q->data[q->front];q->front = (q->front + 1) % q->capacity; // front 指针使用取模运算前进return 1;
}第 4 步:收尾工作(销毁队列)
void destroyQueue(CircularQueue* q) {if (q) {free(q->data); // 先释放数组free(q); // 再释放结构体}
}通过这个从“直觉”到“缺陷”再到“完善”的推导过程,我们就从第一性原理出发,构建了一个健壮、高效的基于数组的循环队列。每一步代码的演进都是为了解决上一步遇到的问题,这正是数据结构设计的精髓所在。
