当前位置：首页 > news >正文

决策树回归：用“分而治之”的智慧，搞定非线性回归难题（附3D可视化）

news 2025/8/14 18:18:04

你有没有遇到过这样的回归问题：特征和目标的关系不是直线，而是弯弯曲曲的非线性关系？比如“温度越高，反应速度先增后减”“时间越长，产品质量下降的速率越来越快”。这时候，线性回归只能画直线，拟合效果差；SVR虽然能处理非线性，但结果像“黑箱”，说不清道理。

今天要讲的决策树回归，堪称解决这类问题的“实用派”：它用“分而治之”的思路，把复杂数据切成一小块一小块，每块用简单常数预测，既能捕捉非线性关系，又能说清“为什么这么预测”。从原理到代码，一次讲透决策树回归的核心逻辑，附3D可视化，帮你看懂它如何“拆解”复杂问题。

一、决策树回归：把复杂问题“拆”成简单问题

决策树回归的核心思想特别朴素：与其用一个复杂函数拟合所有数据，不如把数据分成多个小群体，每个群体用一个简单值（比如均值）预测。

举个例子：预测“化学反应速度”（目标），特征是“温度”和“时间”。数据分布可能很复杂——低温时，时间越长反应越快；高温时，时间太长反应反而变慢。

决策树回归会这样处理：

先找一个“最佳分裂点”（比如温度=500℃），把数据分成“低温组”和“高温组”；
对“低温组”，再找时间的分裂点（比如时间=5小时），分成“短时”和“长时”，分别用各自的平均反应速度预测；
对“高温组”，同样按时间分裂，用各组均值预测。

最终，整个数据被拆成多个小区域，每个区域的预测值就是该区域的平均反应速度——简单直接，还能说清“为什么这个样本预测值是X”（因为它属于低温+短时组，该组平均就是X）。

二、核心原理：如何找到“最佳分裂点”？

决策树回归的关键是递归分裂：从根节点开始，每次选一个特征和一个分裂点，把数据分成两部分，直到满足停止条件（如树深度足够、样本太少）。

1. 分裂的“好坏”用损失函数衡量

判断一个分裂点是否“最佳”，要看分裂后的数据“更集中”还是“更分散”。回归问题中最常用均方误差（MSE） 作为损失函数：

$MSE=1n∑i=1n(yi−y^)2\text{MSE} = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y})^2$

其中， $y_i$ 是样本真实值， $y^\hat{y}$ 是该区域的预测值（通常是均值）。

分裂的目标是：让分裂后两部分的总MSE尽可能小。

比如，分裂前整体MSE是100；分裂后，左半部分MSE=30，右半部分MSE=20，总MSE=50（小于100）——这个分裂就是有效的，让数据更“集中”。

2. 分裂的完整流程（以单特征为例）

假设特征是“温度”，目标是“反应速度”，分裂步骤：

遍历温度的所有可能值（比如300℃、400℃、500℃…）作为候选分裂点；
对每个候选点，把数据分成“温度≤T”和“温度>T”两组；
计算两组的MSE，并求和（总MSE）；
选择总MSE最小的T作为最佳分裂点；
对分裂后的两组，重复上述步骤（递归分裂），直到满足停止条件（如树深度=5，或每组样本<10个）。

3. 多特征怎么办？逐个尝试，选最优

实际问题往往有多个特征（比如“温度”和“时间”），决策树会：

对每个特征，按上述步骤计算“最佳分裂点”和对应的总MSE；
选“总MSE最小”的那个特征和分裂点，完成本次分裂。

比如，对“温度”分裂的总MSE=50，对“时间”分裂的总MSE=40——就选“时间”作为本次分裂的特征。

三、决策树回归 vs 其他回归：优势在哪里？

回归方法	特点	适合场景	缺点
线性回归	拟合直线，简单易解释	特征与目标线性相关	无法处理非线性、特征交互
多项式回归	拟合曲线，处理轻度非线性	明确的低次非线性关系	高次易过拟合，特征多时有维度灾难
SVR（核方法）	处理复杂非线性	高维、非线性数据	结果难解释，参数调优复杂
决策树回归	分区域用常数预测，易解释	非线性、特征交互多、需解释性	易过拟合，对噪声敏感

决策树回归的核心优势：

能捕捉复杂非线性：不管数据是U型、S型还是分段变化，都能通过分裂拟合；
无需特征缩放：温度（℃）和时间（小时）单位不同也不影响，省去标准化步骤；
可解释性强：能画出“决策规则”（比如“温度≤500℃且时间≤5小时→预测值=20”），业务人员也能看懂；
自动处理特征交互：比如“低温时时间影响大，高温时时间影响小”这种交互关系，无需手动构造特征。

四、代码实战：用决策树回归预测化学反应速度

我们用“温度”和“时间”预测“反应速度”（非线性关系），演示决策树回归的完整流程，重点看它如何拟合复杂曲面。

完整代码（可直接运行）

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from mpl_toolkits.mplot3d import Axes3D  # 3D绘图工具# 设置中文显示
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False  # 负号正常显示# ----------------------
# 1. 生成非线性数据（温度、时间→反应速度）
# ----------------------
np.random.seed(42)  # 固定随机种子，结果可复现
n_samples = 1000  # 1000个样本# 特征：温度（20-1000℃）、时间（1-10小时）
temperature = np.random.uniform(20, 1000, n_samples)  # 均匀分布
time = np.random.uniform(1, 10, n_samples)# 目标：反应速度（非线性关系：温度^1.5 - 时间^2 + 噪声）
reaction_speed = 0.05 * (temperature**1.5) - 0.5 * (time**2) + np.random.normal(0, 5, n_samples)# 整理成DataFrame
data = pd.DataFrame({'温度': temperature,'时间': time,'反应速度': reaction_speed
})# ----------------------
# 2. 训练决策树回归模型
# ----------------------
# 特征（温度、时间）和目标（反应速度）
X = data[['温度', '时间']]
y = data['反应速度']# 初始化模型：max_depth=5（控制树深度，防止过拟合）
model = DecisionTreeRegressor(max_depth=5, random_state=42)
model.fit(X, y)  # 训练模型# ----------------------
# 3. 预测与可视化：3D曲面展示非线性拟合
# ----------------------
# 生成网格数据（覆盖温度和时间的取值范围）
temp_range = np.linspace(20, 1000, 100)  # 温度从20到1000，取100个点
time_range = np.linspace(1, 10, 100)     # 时间从1到10，取100个点
temp_grid, time_grid = np.meshgrid(temp_range, time_range)  # 生成网格# 预测网格上的反应速度
# 先把网格数据展平成二维数组（n行2列），再预测，最后还原成网格形状
X_grid = np.c_[temp_grid.ravel(), time_grid.ravel()]  # 展平
predicted_speed = model.predict(X_grid).reshape(temp_grid.shape)  # 预测并还原形状# ----------------------
# 4. 绘制可视化图表
# ----------------------
fig = plt.figure(figsize=(14, 6))# 子图1：3D曲面图（展示预测的非线性关系）
ax1 = fig.add_subplot(121, projection='3d')
# 绘制预测曲面
surf = ax1.plot_surface(temp_grid, time_grid, predicted_speed,cmap='viridis', edgecolor='none', alpha=0.8
)
ax1.set_xlabel('温度（℃）')
ax1.set_ylabel('时间（小时）')
ax1.set_zlabel('预测反应速度')
ax1.set_title('决策树回归预测的3D曲面', fontsize=14)
fig.colorbar(surf, ax=ax1, shrink=0.5, aspect=5, label='反应速度')  # 颜色条# 子图2：实际值vs预测值（评估拟合效果）
ax2 = fig.add_subplot(122)
y_pred = model.predict(X)  # 对训练集的预测值
# 绘制散点图
ax2.scatter(y, y_pred, c='blue', alpha=0.6, edgecolor='k', s=50, label='预测值')
# 参考线：y=x（越靠近这条线，预测越准）
ax2.plot([y.min(), y.max()], [y.min(), y.max()], 'r--', lw=2, label='理想线（y=x）')
ax2.set_xlabel('实际反应速度')
ax2.set_ylabel('预测反应速度')
ax2.set_title('实际值 vs 预测值', fontsize=14)
ax2.legend()plt.tight_layout()
plt.show()# ----------------------
# 5. 模型评估
# ----------------------
from sklearn.metrics import mean_squared_error, r2_scoremse = mean_squared_error(y, y_pred)  # 均方误差（越小越好）
r2 = r2_score(y, y_pred)            # R²（越接近1越好）
print(f"均方误差（MSE）：{mse:.2f}")
print(f"决定系数（R²）：{r2:.2f}")  # 接近1，说明拟合效果好

在这里插入图片描述

五、结果解读：决策树如何“拆解”非线性关系？

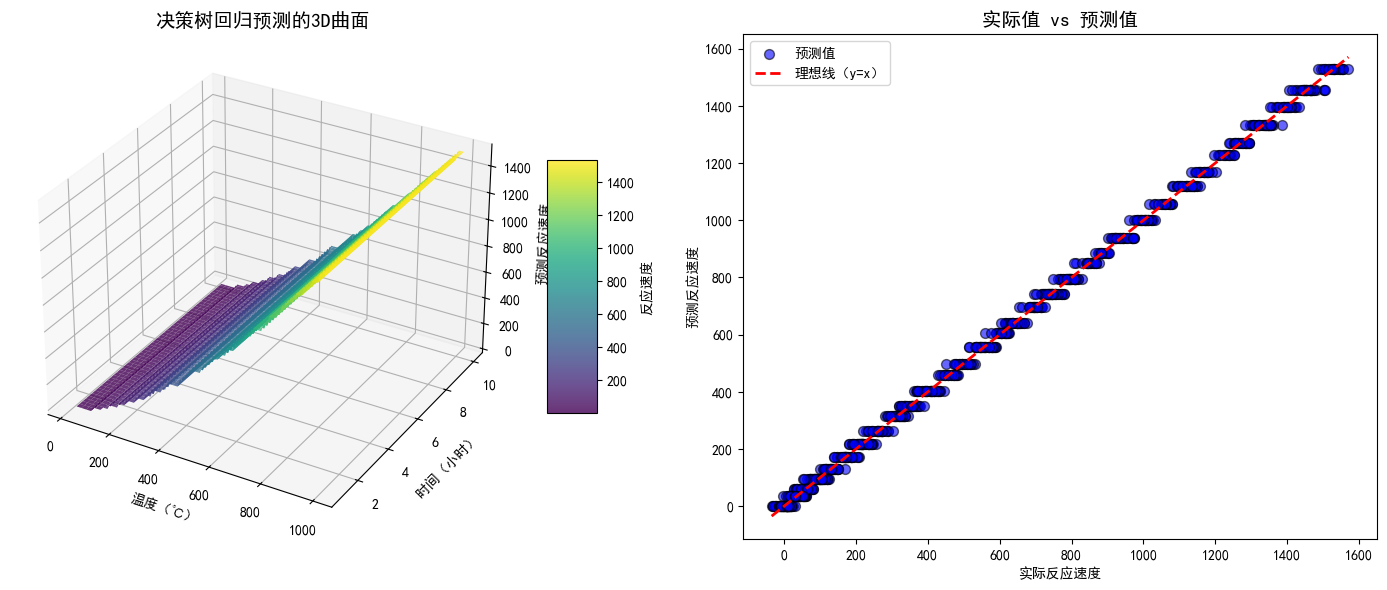
1. 3D曲面图：非线性关系一目了然

左图的3D曲面展示了决策树的预测结果：

温度较低时（比如20-500℃），反应速度随温度升高快速上升（曲面陡峭）；
温度较高时（500-1000℃），反应速度上升变缓；
无论温度高低，时间越长，反应速度越低（曲面沿时间轴向下倾斜）。

这种分段变化的非线性关系，正是决策树通过多次分裂捕捉到的——每个小区域的预测值都是该区域的均值，组合起来就形成了贴合数据的平滑曲面。

2. 实际vs预测图：拟合效果直观判断

右图中，蓝色点越靠近红色虚线（y=x），说明预测值与实际值越接近。本例中，大部分点密集分布在虚线附近，R²接近0.9，说明决策树很好地拟合了数据规律。

六、避坑指南：决策树回归的“雷区”与调参

决策树回归虽好，但有个致命弱点：容易过拟合（树太深会记住噪声，泛化差）。这时候需要通过调参控制树的复杂度：

参数	作用	调优建议
`max_depth`	树的最大深度（分裂次数上限）	太小→欠拟合（拟合不充分）；太大→过拟合，从3-5开始试，逐步增加至验证集效果最优。
`min_samples_split`	分裂节点所需的最小样本数	太小→易过拟合；太大→难分裂，建议5-20。
`min_samples_leaf`	叶节点的最小样本数（分裂后每个组的样本数）	太小→叶节点太多（过拟合）；太大→模型太简单，建议1-5。