数据分析小白训练营:基于python编程语言的Numpy库介绍(第三方库)(下篇)
衔接上篇文章:数据分析小白训练营:基于python编程语言的Numpy库介绍(第三方库)(上篇)
(十一)数组的组合
核心功能:
一、生成基数组
np.arange().reshape() + 基础运算
功能:创建初始数组并进行数值变换
- 示例:
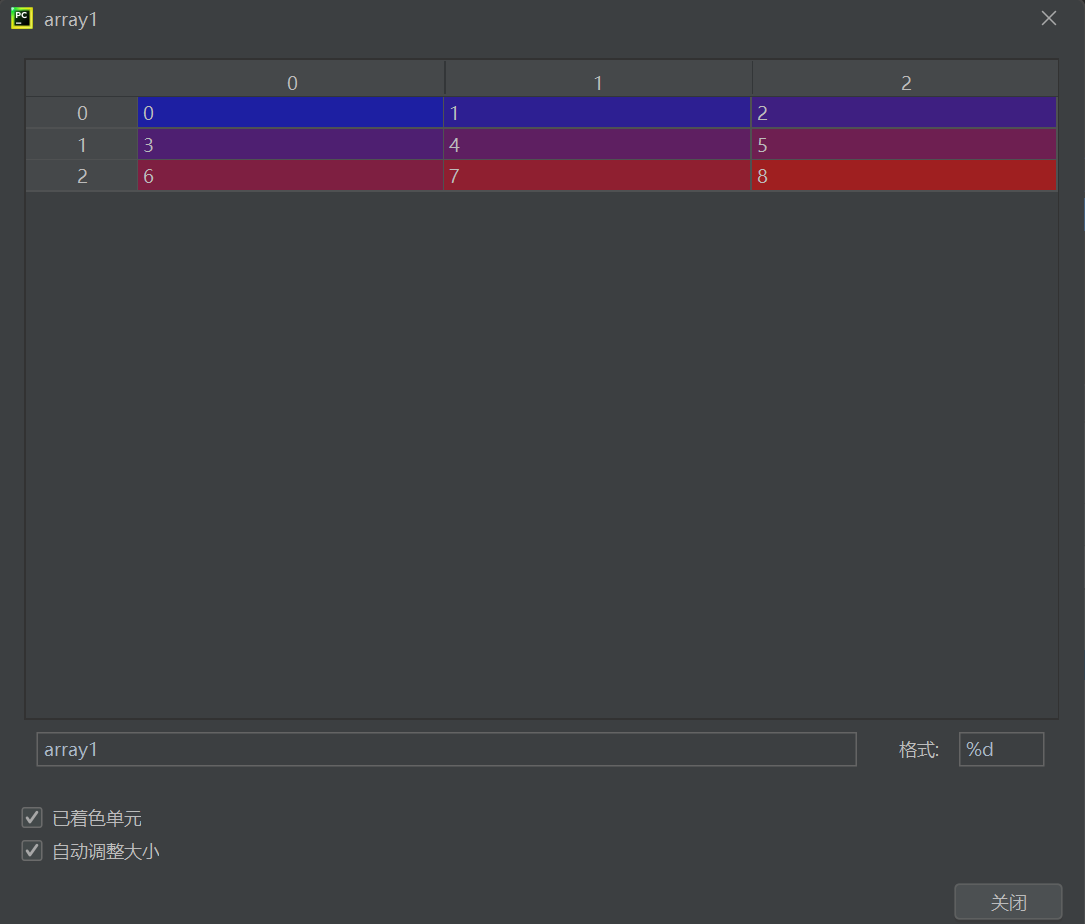
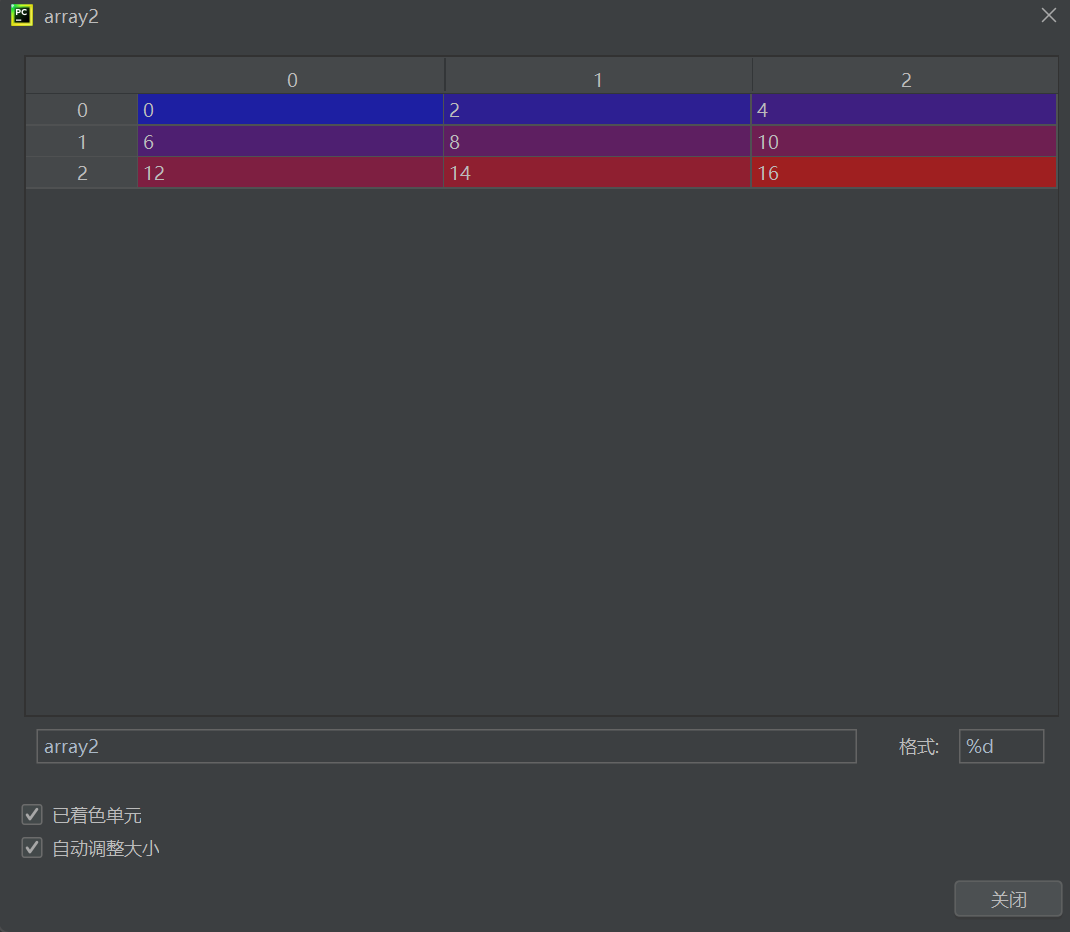
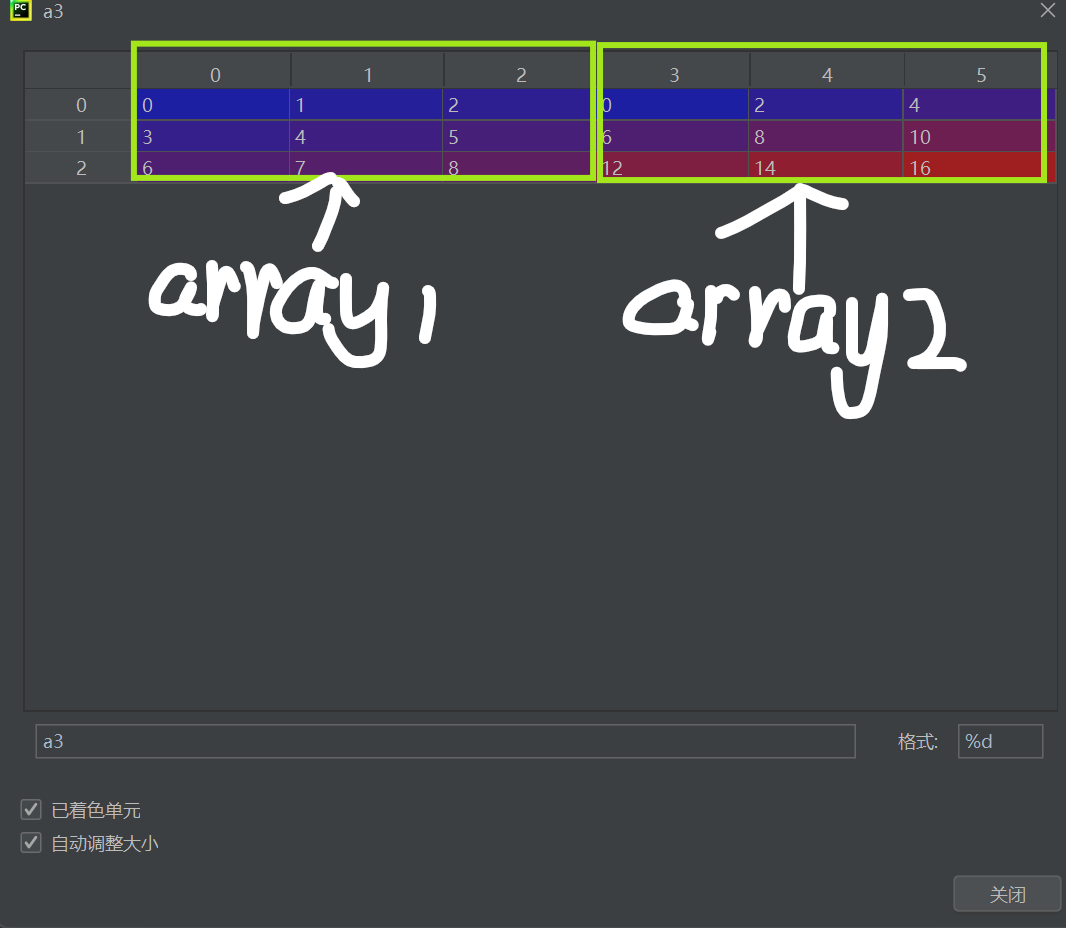
array1 = np.arange(9).reshape(3,3) # 生成3x3矩阵 [[0,1,2],[3,4,5],[6,7,8]] array2 = 2 * array1 # 逐元素乘以2 → [[0,2,4],[6,8,10],[12,14,16]] 关键操作:
np.arange(9):生成0~8的一维数组.reshape(3,3):重塑为3行3列的二维数组2 * array1:利用广播机制对每个元素进行标量乘法
二、水平组合(横向拼接)
np.hstack() 与 np.concatenate(axis=1)
功能:将多个数组沿列方向(水平)拼接
示例:
a3 = np.hstack((array1, array2)) # 拼接后形状: 3x6 a4 = np.hstack((array2, array1)) # 交换顺序拼接 a5 = np.hstack((array1, array2, array1)) # 连续拼接三个数组 a6 = np.concatenate((array1, array2), axis=1) # 等价于hstack特点:
hstack:专门用于水平拼接,自动按列对齐concatenate(axis=1):通过指定轴实现相同效果,灵活性更高
三、垂直组合(纵向拼接)
np.vstack() 与 np.concatenate(axis=0)
功能:将多个数组沿行方向(垂直)拼接
- 示例:
a7 = np.vstack((array2, array1)) # 拼接后形状: 6x3 a8 = np.concatenate((array1, array2), axis=0) # 等价于vstack 特点:
vstack:专门用于垂直拼接,自动按行对齐concatenate(axis=0):通过指定轴实现相同效果,适用于多数组拼接
关键区别总结:
| 操作类型 | 语法示例 | 拼接方向 | 维度变化 | 适用场景 |
|---|---|---|---|---|
np.hstack() | hstack((A, B)) | 水平 | 列数相加 | 合并同类特征的不同样本 |
concatenate(axis=1) | concatenate((A,B), axis=1) | 水平 | 同上 | 更灵活的多数组拼接 |
np.vstack() | vstack((A, B)) | 垂直 | 行数相加 | 堆叠不同样本的数据 |
concatenate(axis=0) | concatenate((A,B), axis=0) | 垂直 | 同上 | 更灵活的多数组拼接 |
示例代码:
import numpy as np#生成基数组
array1 = np.arange(9).reshape(3,3)
array2 = 2*array1
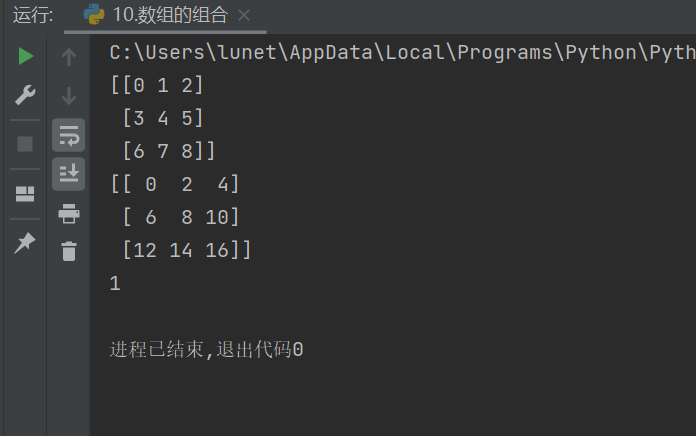
print(array1)
print(array2)#水平组合
a3 = np.hstack((array1,array2))#水平方向变长
a4 = np.hstack((array2,array1))
a5 = np.hstack((array1,array2,array1))a6 = np.concatenate((array1,array2),axis=1)#1为水平组合,0为垂直组合#垂直组合
a7 = np.vstack((array2,array1))a8 = np.concatenate((array1,array2),axis=0)
print(1)
(十二)numpy内数组元素的切割
核心功能:
一、创建基础数组
np.arange().reshape()
功能:生成连续数值并重塑为指定形状的二维数组
示例:
array1 = np.arange(16).reshape(4,4) # 生成4x4矩阵 [[0,1,2,3],[4,5,6,7],...] print(array1)关键点:
np.arange(16)生成0~15的一维数组,.reshape(4,4)将其重塑为4行4列的二维数组
二、等分切割(严格均分)
1. 水平切割(沿列方向)
方法1:
np.hsplit(array, n)功能:将数组沿水平方向(列)均分为
n等份示例:
a = np.hsplit(array1, 2)→ 将4列均分为2份,每份2列,返回两个形状为(4,2)的子数组
方法2:
np.split(array, n, axis=1)功能:与
hsplit等价,通过axis=1明确指定列方向示例:
b = np.split(array1, 2, axis=1)→ 结果同a
2. 垂直切割(沿行方向)
方法1:
np.vsplit(array, n)功能:将数组沿垂直方向(行)均分为
n等份示例:
c = np.vsplit(array1, 2)→ 将4行均分为2份,每份2行,返回两个形状为(2,4)的子数组
方法2:
np.split(array, n, axis=0)功能:与
vsplit等价,通过axis=0明确指定行方向示例:
d = np.split(array1, 2, axis=0)→ 结果同c
三、强制切割(允许不等分)
1. 水平强制切割
函数:
np.array_split(array, n, axis=1)功能:将数组沿水平方向(列)强制分为
n份,允许不等分示例:
e = np.array_split(array1, 3, axis=1)→ 将4列分为3份,前两份各2列,最后一份0列(实际为2列,因余数分配)特点:若无法均分,余数会分配到前面的块中
2. 垂直强制切割
函数:
np.array_split(array, n, axis=0)功能:将数组沿垂直方向(行)强制分为
n份,允许不等分示例:
f = np.array_split(array1, 3, axis=0)→ 将4行分为3份,前两块各2行,最后一块0行(实际为0行,但此处无意义)
四、非均匀数组的强制切割
示例:5x5数组的切割
代码:
array1 = np.arange(25).reshape(5,5) # 5x5矩阵 g = np.array_split(array1, 3, axis=1) # 水平切分为3份 h = np.array_split(array1, 3, axis=0) # 垂直切分为3份特点:
水平切割:5列分为3份 → 前两块各2列,最后一块1列
垂直切割:5行分为3份 → 前两块各2行,最后一块1行
关键区别总结:
| 函数 | 是否允许不等分 | 切割方向 | 适用场景 |
|---|---|---|---|
np.hsplit() | 否 | 水平 | 严格均分列 |
np.vsplit() | 否 | 垂直 | 严格均分行 |
np.split(axis=1) | 否 | 水平 | 同 hsplit |
np.split(axis=0) | 否 | 垂直 | 同 vsplit |
np.array_split() | 是 | 任意 | 需处理不等分场景(如数据不足) |
代码示例:
import numpy as nparray1 = np.arange(16).reshape(4,4)
print(array1)#水平切割
a = np.hsplit(array1,2)#其中第二个参数2,表示将矩阵array1进行2等份的切分
print(a)b = np.split(array1,2,axis=1)#垂直切割
c = np.vsplit(array1,2)
d = np.split(array1,2,axis=0)#强制切割
#水平切割
e = np.array_split(array1,3,axis=1)#垂直切割
f = np.array_split(array1,3,axis=0)###########################################
array1 = np.arange(25).reshape(5,5)
print(array1)g = np.array_split(array1,3,axis=1)h = np.array_split(array1,3,axis=0)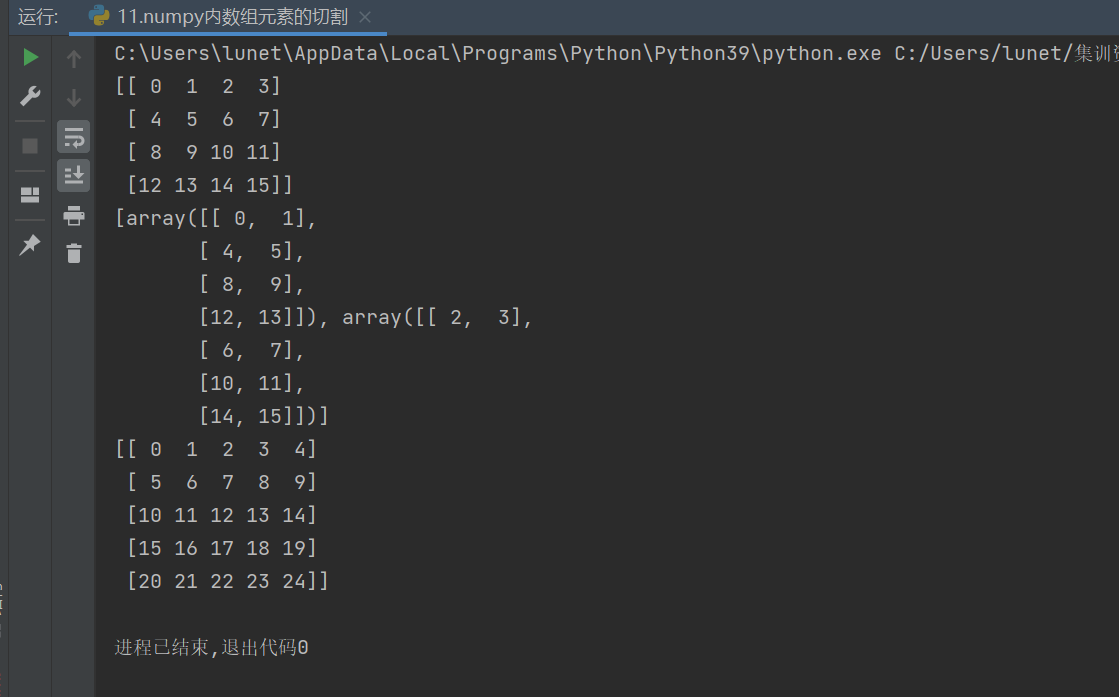
(十三)数组的算数运算
核心功能:
一、创建基础数组
np.arange().reshape()
功能:生成指定范围内的等差数列并重塑为指定形状的数组
示例:
array1 = np.arange(1,5,1).reshape(2,2) # 生成 [[1,2],[3,4]]关键参数:
np.arange(1,5,1):起始值=1,终止值=5(不含),步长=1 → 生成[1,2,3,4].reshape(2,2):将一维数组重塑为2行2列的二维数组
标量乘法生成新数组
功能:通过标量乘法快速生成关联数组
示例:
array2 = 2 * array1 # 每个元素乘以2 → [[2,4],[6,8]]特点:利用 NumPy 的广播机制,标量自动扩展至与数组同形
二、逐元素数学运算
1. 加法 +
功能:对应位置元素相加
示例:
print(array1 + array2) # 输出: [[3,6],[9,12]]计算逻辑:
1+2=3,2+4=6,3+6=9,4+8=12
2. 减法 -
功能:对应位置元素相减
示例:
print(array1 - array2) # 输出: [[-1,-2],[-3,-4]]计算逻辑:
1-2=-1,2-4=-2,3-6=-3,4-8=-4
3. 乘法 *
功能:对应位置元素相乘
示例:
print(array1 * array2) # 输出: [[2,8],[18,32]]计算逻辑:
1×2=2,2×4=8,3×6=18,4×8=32
4. 除法 /
功能:对应位置元素相除
示例:
print(array1 / array2) # 输出: [[0.5,0.5],[0.5,0.5]]计算逻辑:
1/2=0.5,2/4=0.5,3/6=0.5,4/8=0.5
5. 取余 %
功能:对应位置元素取余数
示例:
print(array2 % array1) # 输出: [[0,0],[0,0]]计算逻辑:
2%1=0,4%2=0,6%3=0,8%4=0
6. 整除 //
功能:对应位置元素整除(向下取整)
示例:
print(array1 // array2) # 输出: [[0,0],[0,0]]计算逻辑:
1//2=0,2//4=0,3//6=0,4//8=0
示例代码:
import numpy as nparray1 = np.arange(1,5,1).reshape(2,2)
array2 = 2*array1
print(array1)
print(array2)#数组的加法【对应位置的元素求和】
print(array1 + array2)#数组的减法[对应位置元素相减]
print(array1 - array2)#数组的乘法【对应位置相乘】
print(array1 * array2)#数组的除法[对应位置相除]
print(array1 / array2)#数组的取余(%)
print(array2 % array1)#数组的取整
print(array1 // array2)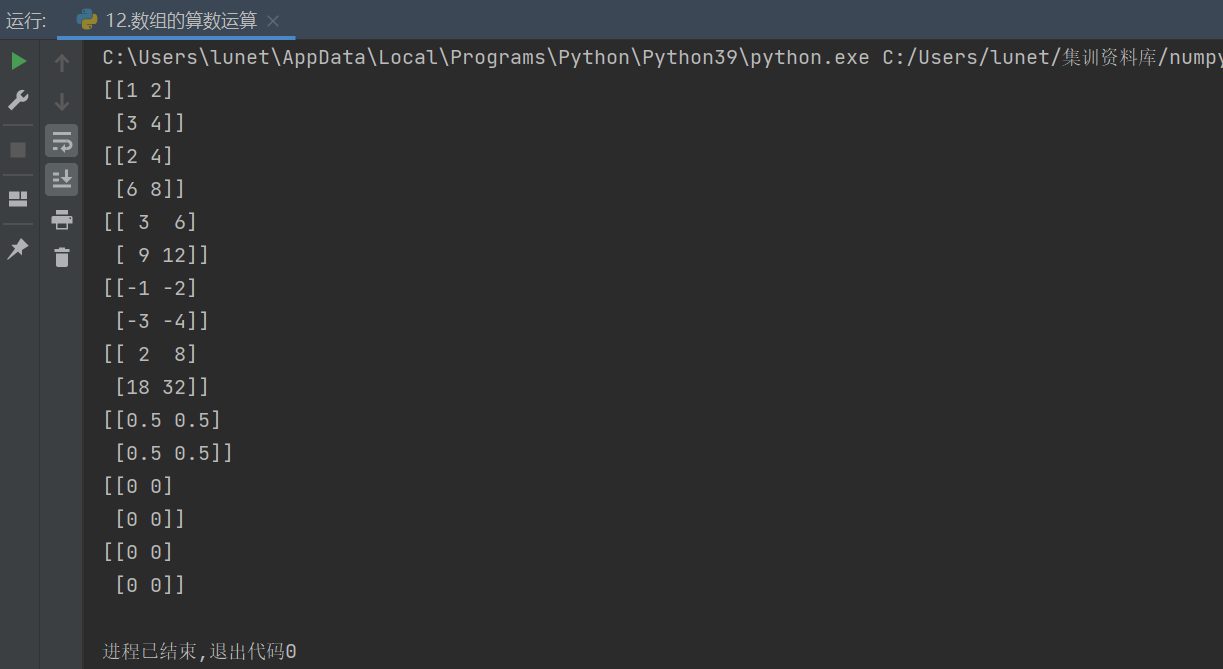
(十四)数组的深拷贝与浅拷贝
NumPy 中浅拷贝与深拷贝的本质区别:
- 浅拷贝:通过直接赋值实现,新旧数组共享内存,修改其一会影响另一者。
- 深拷贝:通过
.copy()方法创建独立副本,修改副本不影响原数组
核心功能:
1. 创建原始数组
array1 = np.array([1,2,3]) # 创建一维数组 [1,2,3]
- 作用:初始化一个包含
[1,2,3]的 NumPy 数组
2. 浅拷贝(引用赋值)
array2 = array1 # 浅拷贝:仅传递引用
- 本质:
array2和array1共享同一块内存,修改任一变量会影响另一个 - 验证:
array2[0] = 100 # 修改 array2 的第一个元素 print(array2) # 输出: [100, 2, 3] print(array1) # 输出: [100, 2, 3] ← 原数组也被修改! - 结论:浅拷贝不安全,对副本的修改会直接影响原数组
3. 深拷贝(独立副本)
array3 = array1.copy() # 深拷贝:创建独立副本
- 本质:
array3是array1的完全独立副本,拥有独立内存空间 - 验证:
array3[0] = 10 # 修改 array3 的第一个元素 print(array3) # 输出: [10, 2, 3] print(array1) # 输出: [1, 2, 3] ← 原数组未被修改! - 结论:深拷贝安全,对副本的修改不影响原数组
关键区别总结:
| 操作 | 内存机制 | 修改影响 | 适用场景 |
|---|---|---|---|
| 浅拷贝 | 共享原数组内存 | 修改副本 → 影响原数组 | 无需保留原数据时(需谨慎使用) |
| 深拷贝 | 创建独立内存 | 修改副本 → 不影响原数组 | 需保留原数据时(推荐使用) |
示例代码:
import numpy as nparray1 = np.array([1,2,3])
#浅拷贝
array2 = array1#更改array2的元素的值
array2[0] = 100
print(array2)
print("#####################")
print(array1)#深拷贝
array3 = array1.copy()
array3[0] = 10
print(array3)
print("##################")
print(array1)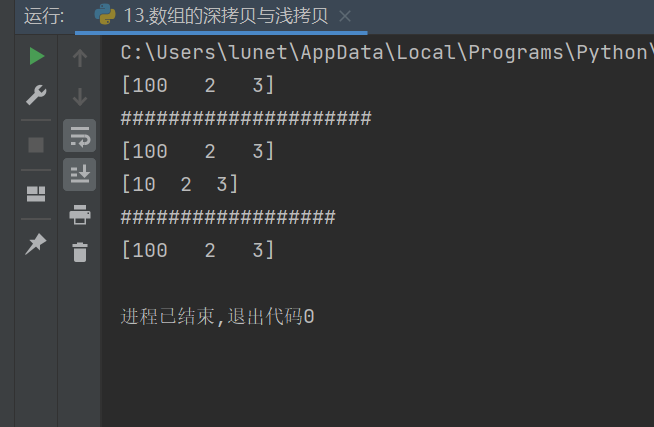
(十五)numpy内的随机模块儿(一)
核心功能:
1. 导入依赖库
import numpy as np
import matplotlib.pyplot as plt
作用:引入 NumPy(高效数值计算)和 Matplotlib(数据可视化)库
2. 设置随机种子
np.random.seed(1000) # 固定随机种子以保证结果可复现
关键作用:锁定随机数生成器的初始状态,使后续所有随机操作的结果在多次运行中保持一致(便于调试和验证)
3. 生成单个随机整数
r1 = np.random.randint(0, 10) # 左闭右开区间 [0, 10)
print(r1)
功能:从
[0, 10)的左闭右开区间内随机抽取一个整数示例输出:若种子为1000,则固定输出
8(可通过多次运行验证)
4. 生成随机数组
a = []
for i in range(10):a0 = np.random.randint(0, 10) # 每次独立生成一个随机整数a.append(a0)
print(a)
功能:循环10次,每次生成一个
[0, 10)范围内的随机整数,存入列表a特点:由于已设置随机种子,即使重启程序,只要种子不变,生成的序列也完全相同
示例输出:
[8, 7, 9, 5, 8, 7, 6, 8, 5, 7](种子1000下的固定结果)
5. 绘制直方图
a = []
for i in range(10):a0 = np.random.randint(0, 10) # 每次独立生成一个随机整数a.append(a0)
print(a)
功能:统计列表
a中各数值的出现频率,并以柱状图形式可视化参数说明:
color='r':设置柱子颜色为红色plt.show():渲染并显示图像窗口
预期效果:展示10个随机数在
[0, 10)区间内的分布情况(因样本量较小,可能呈现非完美均匀分布)
示例代码:
import numpy as np
import matplotlib.pyplot as plt
"""
randint(start,end):
产生一个随机整数
(0,10) ->左闭右开的区间
"""
#随机种子
np.random.seed(1000)#矩阵类型随机
r1 = np.random.randint(0,10)
print(r1)#
a = []
for i in range(10):a0 = np.random.randint(0,10)a.append(a0)
print(a)
plt.hist(a,color='r')
plt.show()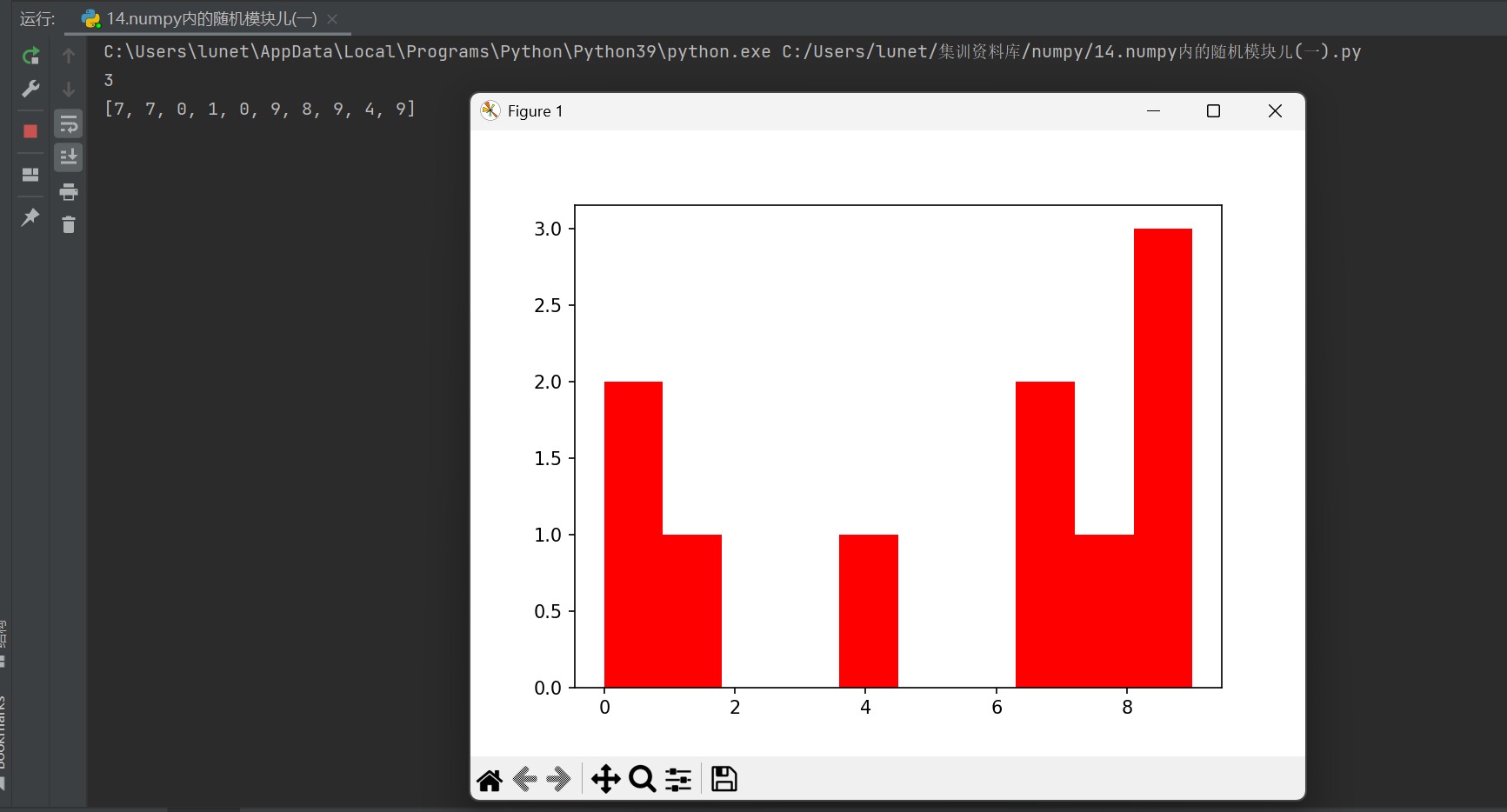
(十六)numpy内的随机模块儿(二)
核心功能:
1. 单次随机浮点数 np.random.rand()
r1 = np.random.rand() # 生成 [0,1) 区间内的随机浮点数
print(r1)功能:返回一个服从 均匀分布 的随机浮点数,取值范围
[0, 1)特点:无参数,适用于简单随机采样场景
示例输出:如
0.7892(每次运行不同)
2. 标准正态分布随机数 np.random.normal()
r1 = np.random.rand() # 生成 [0,1) 区间内的随机浮点数
print(r1)
功能:从 标准正态分布(均值 μ=0,标准差 σ=1)中抽取一个样本
扩展性:可通过参数调整均值和标准差(见后续示例)
示例输出:如
1.2345(可能为负值)
3. 生成随机整数矩阵 np.random.randint()
r3 = np.random.randint(0, 10, size=(5,5)) # 生成 5x5 的 [0,10) 区间内随机整数矩阵
print(r3)
功能:创建指定形状的整数矩阵,元素取自
[low, high)区间关键参数:
low=0,high=10:左闭右开区间size=(5,5):输出形状为 5 行 5 列
示例输出:
[[3 7 9 1 5][8 2 6 4 0]...]
4. 生成均匀分布浮点矩阵 np.random.rand()
r4 = np.random.rand(5,5) # 生成 5x5 的 [0,1) 区间内随机浮点矩阵
print(r4)
功能:创建指定形状的浮点数矩阵,元素服从
[0,1)均匀分布优势:比循环更高效,直接生成多维数组
示例输出:全为
0~1之间的浮点数
5. 生成自定义正态分布矩阵 np.random.normal()
r5 = np.random.normal(5, 10, size=(5,5)) # 生成均值 μ=5,标准差 σ=10 的正态分布矩阵
print(r5)
功能:创建指定形状的正态分布矩阵,可自定义均值和标准差
参数说明:
loc=5:均值 μscale=10:标准差 σsize=(5,5):输出形状
示例输出:大部分值集中在
5 ± 3×10范围内(约-25 ~ 35)
关键区别总结:
| 函数 | 分布类型 | 取值范围 | 典型用途 |
|---|---|---|---|
np.random.rand() | 均匀分布 | [0, 1) | 简单随机采样、初始化权重 |
np.random.normal() | 正态分布 | (-∞, +∞) | 模拟自然现象、噪声添加 |
np.random.randint() | 离散均匀分布 | [low, high) | 生成随机索引、分类标签 |
np.random.rand() | 连续均匀分布 | [0, 1) | 快速生成多维随机浮点矩阵 |
np.random.normal() | 自定义正态分布 | (μ - kσ, μ + kσ) | 数据增强、蒙特卡洛模拟 |
示例代码:
import numpy as np"""
rand() ->(0,1)之间的随机浮点数
"""
#np.random.seed(100)
r1 = np.random.rand()
print(r1)"""
normal() ->生成一些符合正态分布的数据
N~(0,1)
"""
r2 = np.random.normal()
print(r2)
#################################
#生成随机数矩阵r3 = np.random.randint(0,10,size=(5,5))
print(r3)r4 = np.random.rand(5,5)
print(r4)r5 = np.random.normal(5,10,size=(5,5))
print(r5)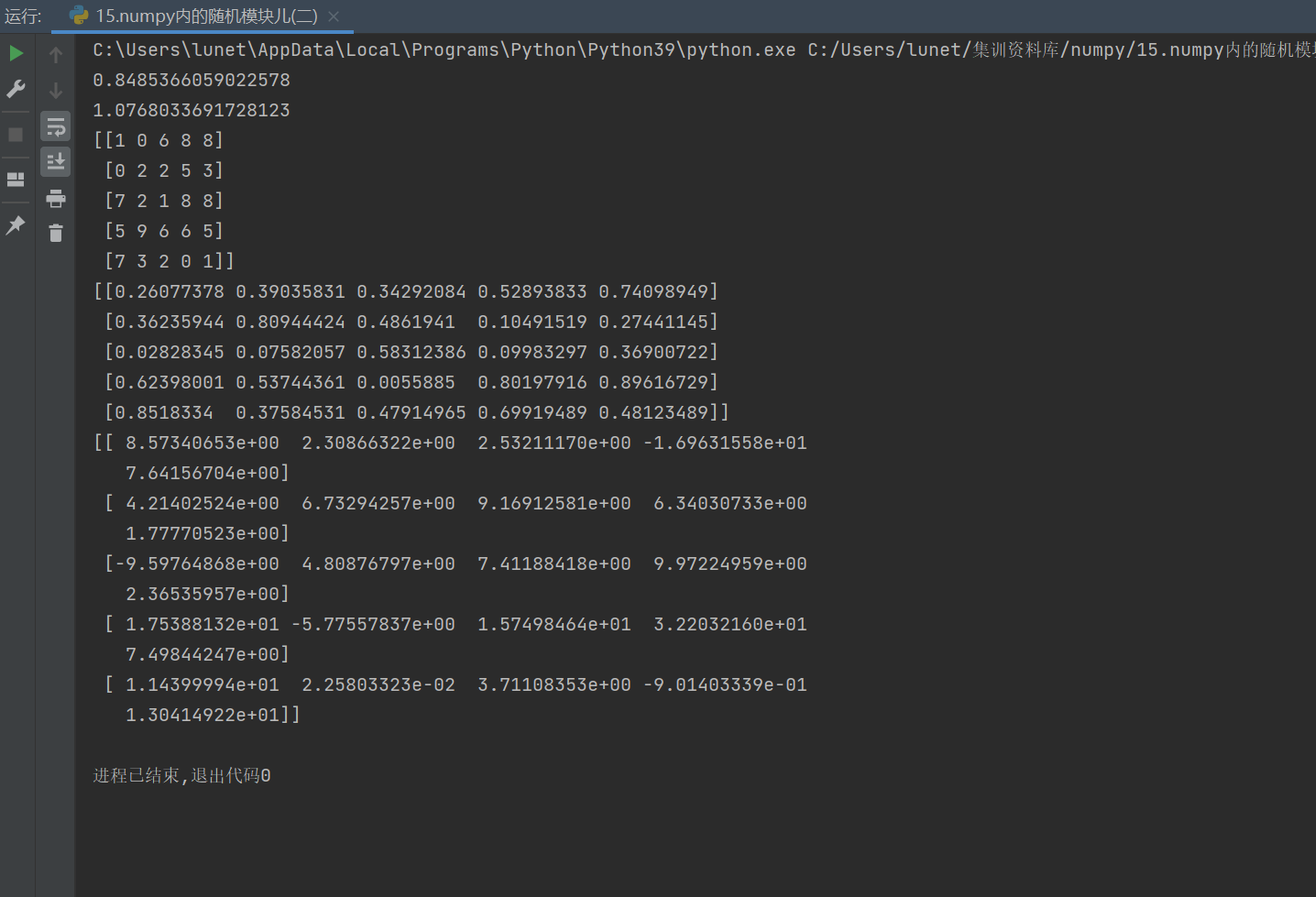
(十七)numpy内一些函数的使用
核心功能:
1. 生成正态分布随机矩阵
array1 = np.random.normal(size=(3,3)) # 生成3x3的正态分布随机矩阵
print(array1)
功能:创建一个形状为
(3,3)的二维数组,其中每个元素独立采样自标准正态分布(默认均值 μ=0,标准差 σ=1)特点:无需显式指定均值和标准差时,默认使用标准正态分布;若需自定义参数可添加
loc(均值)和scale(标准差)参数示例输出:类似如下结构(具体数值因随机性不同):
[[ 0.4967 1.5292 -0.0769][ 0.2784 0.8655 1.2064][-0.4052 0.1763 0.7658]]
2. 基础统计量计算
# 求方差
print(array1.var()) # 全局方差(所有元素的方差)# 求标准差
a = array1.std() # 全局标准差# 求均值
b = array1.mean() # 全局均值# 求和
c = array1.sum() # 所有元素的总和# 求中位数
d = np.median(array1) # 全局中位数
关键函数:
var():计算数组所有元素的方差(衡量数据离散程度)std():计算标准差(方差的平方根,更直观反映波动幅度)mean():计算算术平均值(数据的中心趋势)sum():对所有元素求和np.median():计算中位数(排序后中间值,抗异常值干扰)
注意:直接调用
array1.median()会报错,需使用np.median(array1)
3. 按行/列求和
# 对矩阵的行求和(axis=1)
e = array1.sum(axis=1) # 每行元素相加,结果为长度为3的一维数组# 对矩阵的列进行求和(axis=0)
f = array1.sum(axis=0) # 每列元素相加,结果为长度为3的一维数组
axis参数含义:axis=1:沿行方向求和(压缩行维度,保留列维度)axis=0:沿列方向求和(压缩列维度,保留行维度)
示例输出:
e:每行的总和,如[1.9489, 2.2793, 0.5369]f:每列的总和,如[0.3699, 2.5710, 1.8953]
关键概念总结:
| 操作 | 功能描述 | 返回值类型 | 典型用途 |
|---|---|---|---|
np.random.normal() | 生成正态分布随机数 | ndarray | 模拟自然现象、初始化权重 |
var() | 计算全局方差 | float | 评估数据离散程度 |
std() | 计算全局标准差 | float | 衡量数据波动范围 |
mean() | 计算全局均值 | float | 获取数据平均水平 |
sum() | 所有元素求和 | float | 快速累加总和 |
np.median() | 计算全局中位数 | float | 避免极端值影响的中心度量 |
sum(axis=1) | 按行求和 | 1D array | 分析每行数据的总效应 |
sum(axis=0) | 按列求和 | 1D array | 分析每列数据的总效应 |
代码示例:
import numpy as nparray1 = np.random.normal(size = (3,3))
print(array1)#一些函数
#求方差
print(array1.var())#求标准差
a = array1.std()#求均值
b = array1.mean()#求和
c = array1.sum()#求中位数
#array1.median()
d = np.median(array1)#求和运算
#对矩阵的行求和
e = array1.sum(axis=1)
#对矩阵的列进行求和
f = array1.sum(axis=0)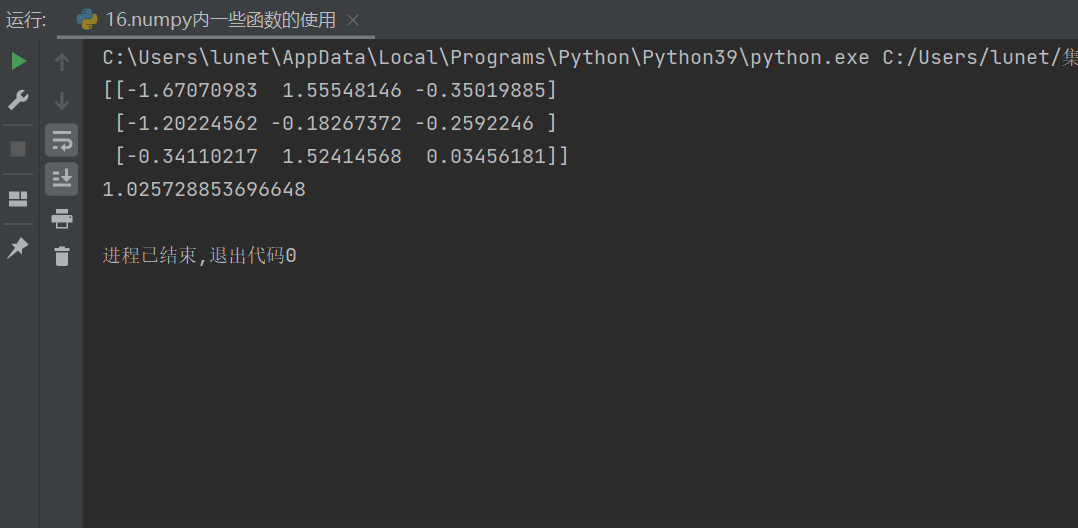
(十八)矩阵的运算
核心功能:
1. 生成基数组
a = np.arange(4).reshape(2,2) # 创建2x2矩阵 [[0,1],[2,3]]
b = a.copy() # 深拷贝生成独立副本
np.arange(4):生成一维数组[0,1,2,3].reshape(2,2):将一维数组重塑为 2 行 2 列的二维矩阵copy():创建深拷贝,确保b与a独立(修改b不影响a)
2. 矩阵乘法
a1 = a.dot(b) # 方法1:通过 .dot() 计算矩阵乘积
a2 = np.dot(a, b) # 方法2:通过 np.dot() 计算矩阵乘积
功能:计算两个 2x2 矩阵的标准矩阵乘积(行列对应相乘再求和)
等价性:两种方法结果相同,均返回新的 2x2 矩阵
数学公式:若
A=[[a,b],[c,d]],B=[[e,f],[g,h]],则AB=[[ae+bg, af+bh], [ce+dg, cf+dh]]
3. 矩阵求逆
a3 = np.linalg.inv(a) # 计算矩阵 a 的逆矩阵
前提:仅当矩阵满秩且行列式不为零时存在逆矩阵
作用:若
a可逆,则a @ a3 == I(单位矩阵),用于求解线性方程组或反转变换风险提示:若矩阵不可逆(如奇异矩阵),会抛出
LinAlgError
4. 自定义矩阵乘法
a4 = a.dot([[-1.5, 0.5], [1. , 0. ]]) # 手动指定第二个矩阵进行乘法
print(a4)
功能:将原始矩阵
a与预定义的 2x2 矩阵相乘,模拟线性变换应用场景:此类操作常见于图像处理(仿射变换)、机器学习特征转换等场景
输出示例:假设
a=[[0,1],[2,3]],则计算过程为:第一行:
0*(-1.5)+1*1=1,0*0.5+1*0=0→[1, 0]第二行:
2*(-1.5)+3*1=-3+3=0,2*0.5+3*0=1→[0, 1]最终结果:
[[1, 0], [0, 1]](单位矩阵)
关键概念总结:
| 操作 | 功能描述 | 注意事项 |
|---|---|---|
np.arange().reshape() | 创建指定形状的初始化矩阵 | 默认按行优先填充数据 |
.copy() | 生成深拷贝,避免共享内存 | 修改副本不影响原数组 |
.dot() / np.dot() | 计算矩阵乘积 | 要求矩阵维度匹配(前导矩阵列数=后继行数) |
np.linalg.inv() | 计算矩阵的逆 | 仅适用于非奇异矩阵(行列式≠0) |
| 自定义矩阵乘法 | 实现线性变换或复合操作 | 可用于验证变换效果或设计特定算法 |
示例代码:
import numpy as np#生成两个基数组
a = np.arange(4).reshape(2,2)
b = a.copy()#矩阵的运算
#加减乘除(求逆)
#加减 ->对应元素加减#矩阵的乘法【点乘】
#a * b
a1 = a.dot(b)
a2 = np.dot(a,b)#矩阵求逆
"""
inv():
并不是所有的矩阵都有逆;
即使你没有逆,给你一个逆【伪逆】
"""
a3 = np.linalg.inv(a)a4 = a.dot([[-1.5, 0.5],[ 1. , 0. ]])
print(a4)
(十九)读取文件
核心功能:
一、np.loadtxt() - 从文本文件加载数据
核心功能
高效读取结构化文本数据:将纯文本文件中的数值数据快速转换为 NumPy 数组
灵活处理分隔符:支持通过 delimiter 参数自定义列分隔符(如 \t、,、空格等)
自动适配行列结构:假设文件中每一行的数值数量相同,按顺序填充到数组的行与列中
代码示例 & 关键参数
data = np.loadtxt('文件读取.txt', delimiter='\t') # 若为CSV文件则用 delimiter=','
print(data)
delimiter: 定义字段分隔符(默认为任意空白字符)- 适用场景:读取传感器日志、CSV/TSV格式数据、科学计算输入文件等
典型应用
# 假设文件内容如下(制表符分隔):
# 1 2 3
# 4 5 6
# 7 8 9# 执行后 data 变为:
array([[1, 2, 3],[4, 5, 6],[7, 8, 9]])
二、np.savetxt() - 将数组保存到文本文件
核心功能
反向操作:将 NumPy 数组以纯文本形式持久化存储
人性化输出:默认以固定宽度排版,便于阅读;可通过 fmt 参数定制数值格式
跨平台兼容:生成标准文本文件,无需依赖特定二进制格式
代码示例 & 关键参数
array = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
np.savetxt('array.txt', array) # 默认用空白分隔
- 扩展性:可添加
fmt='%d'(整数)、delimiter=', '(逗号分隔)等参数 - 适用场景:导出模型预测结果、调试中间变量、与其他工具交换数据
典型输出文件内容
1.00000000e+00 2.00000000e+00 3.00000000e+00
4.00000000e+00 5.00000000e+00 6.00000000e+00
7.00000000e+00 8.00000000e+00 9.00000000e+00对比总结:
| 功能 | np.loadtxt() | np.savetxt() |
|---|---|---|
| 方向 | 文件 → 内存(读取) | 内存 → 文件(写入) |
| 核心用途 | 加载结构化文本数据 | 导出数组为文本文件 |
| 关键参数 | delimiter(解析分隔符) | fmt(控制输出格式) |
| 数据类型限制 | 仅支持数值型数据 | 自动处理浮点数精度 |
| 典型场景 | 数据分析前序步骤 | 结果可视化/长期存档 |
示例代码:
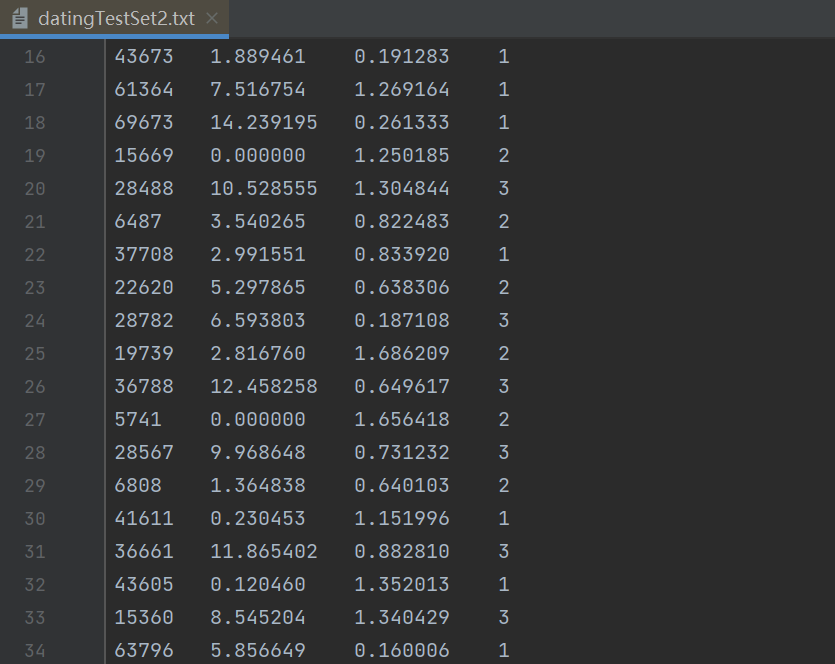
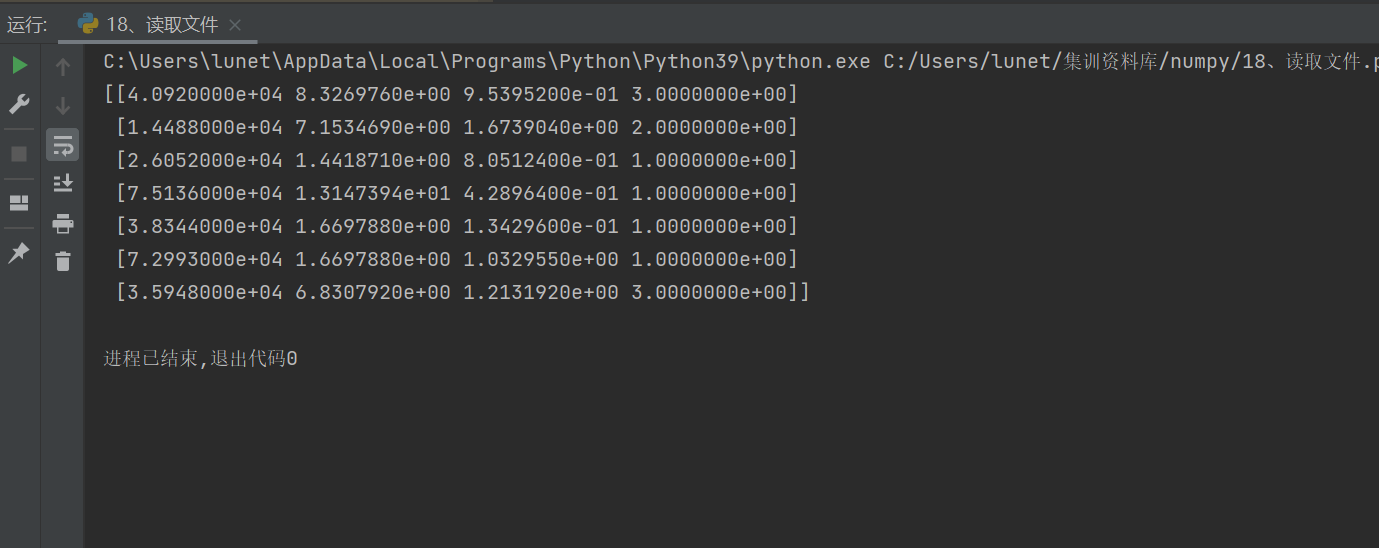
# numpy.loadtxt():从文本文件中加载数据。这个函数假定文件中的每一行都有相同数量的值,并将这些值分隔开。
# 你可以使用 delimiter 参数指定分隔符,如逗号、制表符等。例如:系统的简单介绍这段代码的核心功能
data = np.loadtxt('文件读取.txt', delimiter='\t')#csv格式的文件delimiter=','
print(data)#将数组保存到txt文件中
import numpy as np
array = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])# 创建一个 NumPy 数组
np.savetxt('array.txt', array)# 使用 savetxt() 将数组保存到文本文件中