[优选算法专题一双指针——四数之和]
题目链接
四数之和
题目描述

这道题和三数之和类似,有不懂的可以先看之前的博客:
三数之和
题目解析
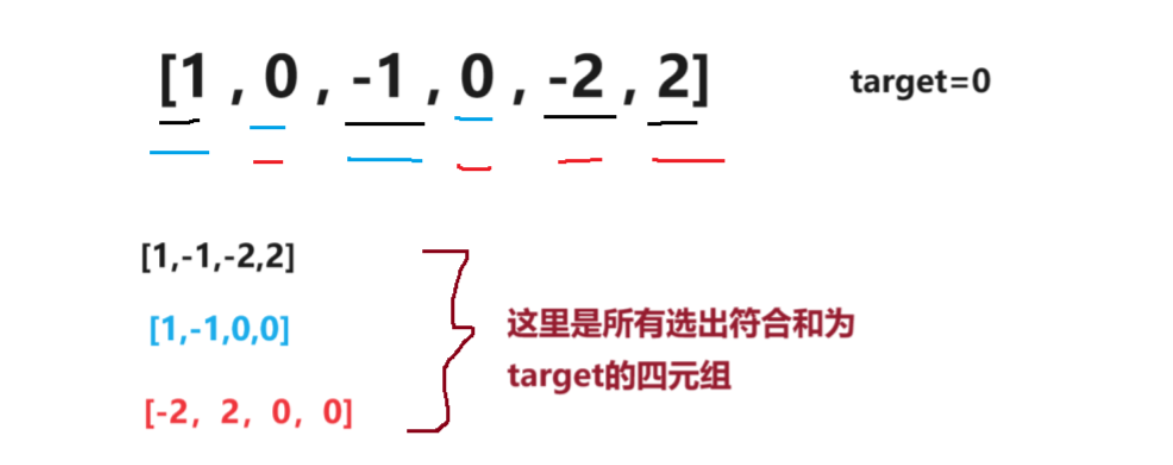
四数之和问题是 LeetCode 中经典的数组类题目,要求在数组中找到所有不重复的四元组,使它们的和等于目标值。这个问题可以看作是两数之和、三数之和的延伸,核心思路是通过排序和双指针技术优化时间复杂度。
解题思路
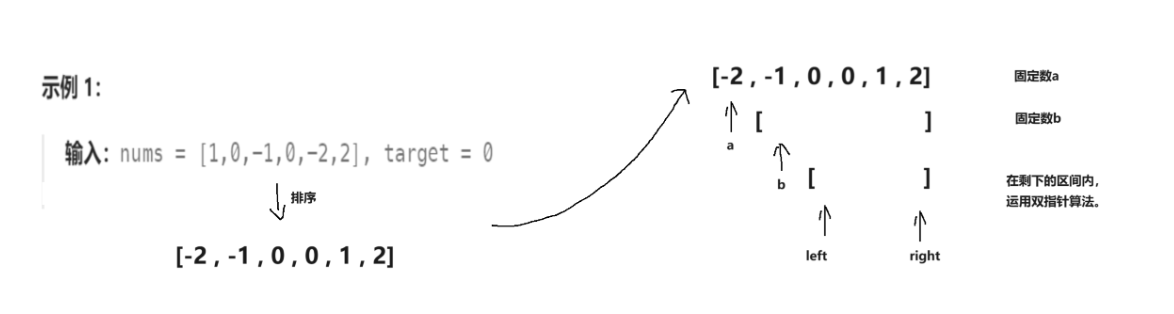
- 排序数组:先对数组进行排序,为后续的去重和双指针操作奠定基础
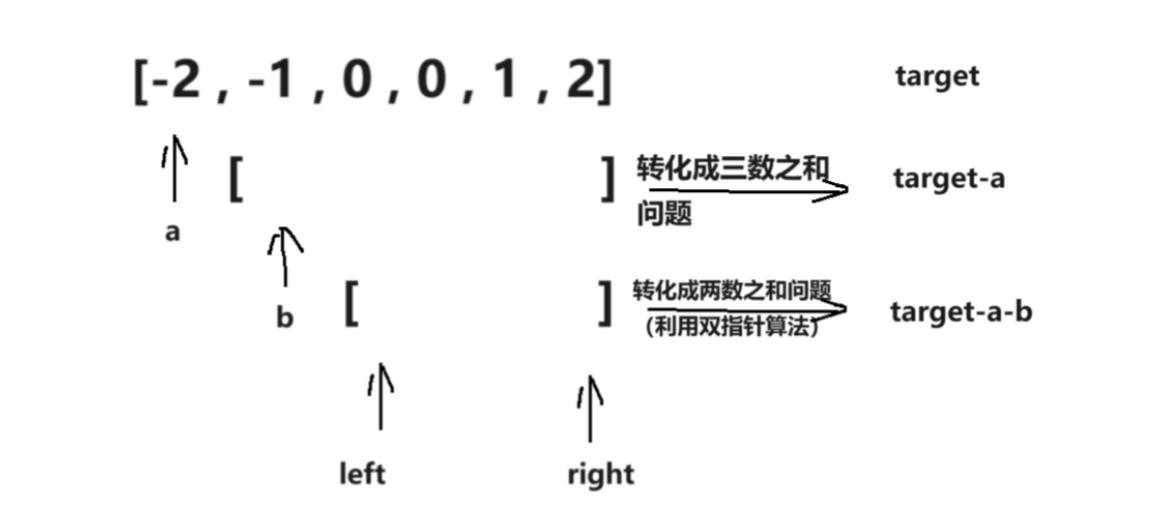
- 固定双指针:使用两层循环固定前两个数
- 移动双指针:用两个指针寻找后两个数,通过调整指针位置使四数之和等于目标值
- 去重处理:在各个环节都要进行去重操作,避免出现重复的四元组
关键技术点解析
1. 排序的作用
- 使相同的元素聚集在一起,便于去重操作
- 可以通过移动指针来调整总和大小(左移减小总和,右移增大总和)
2.去重策略
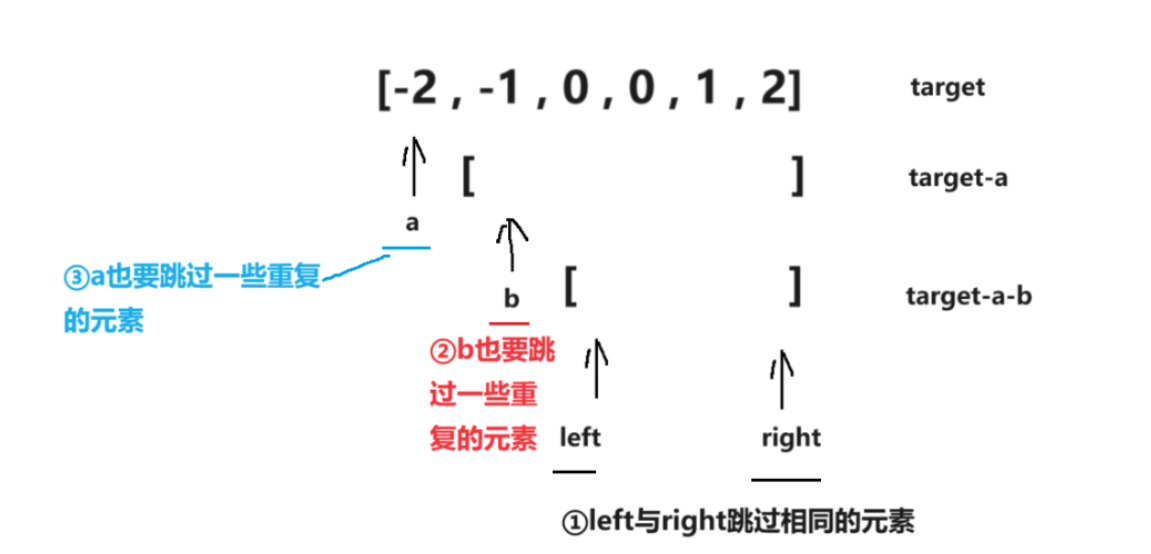
- 第一个数去重:当
nums[i] == nums[i-1]时跳过,避免重复的四元组以相同的第一个数开始 - 第二个数去重:当
nums[j] == nums[j-1]时跳过,避免重复的四元组以相同的前两个数开始 - 第三、四个数去重:找到符合条件的组合后,移动指针并跳过相同值
3. 双指针技巧
- 固定前两个数后,用两个指针从两端向中间移动
- 当总和小于目标值时,左指针右移(增大总和)
- 当总和大于目标值时,右指针左移(减小总和)
- 这种方法将原本 O (n²) 的内层循环优化为 O (n)
4. 溢出处理
完整代码
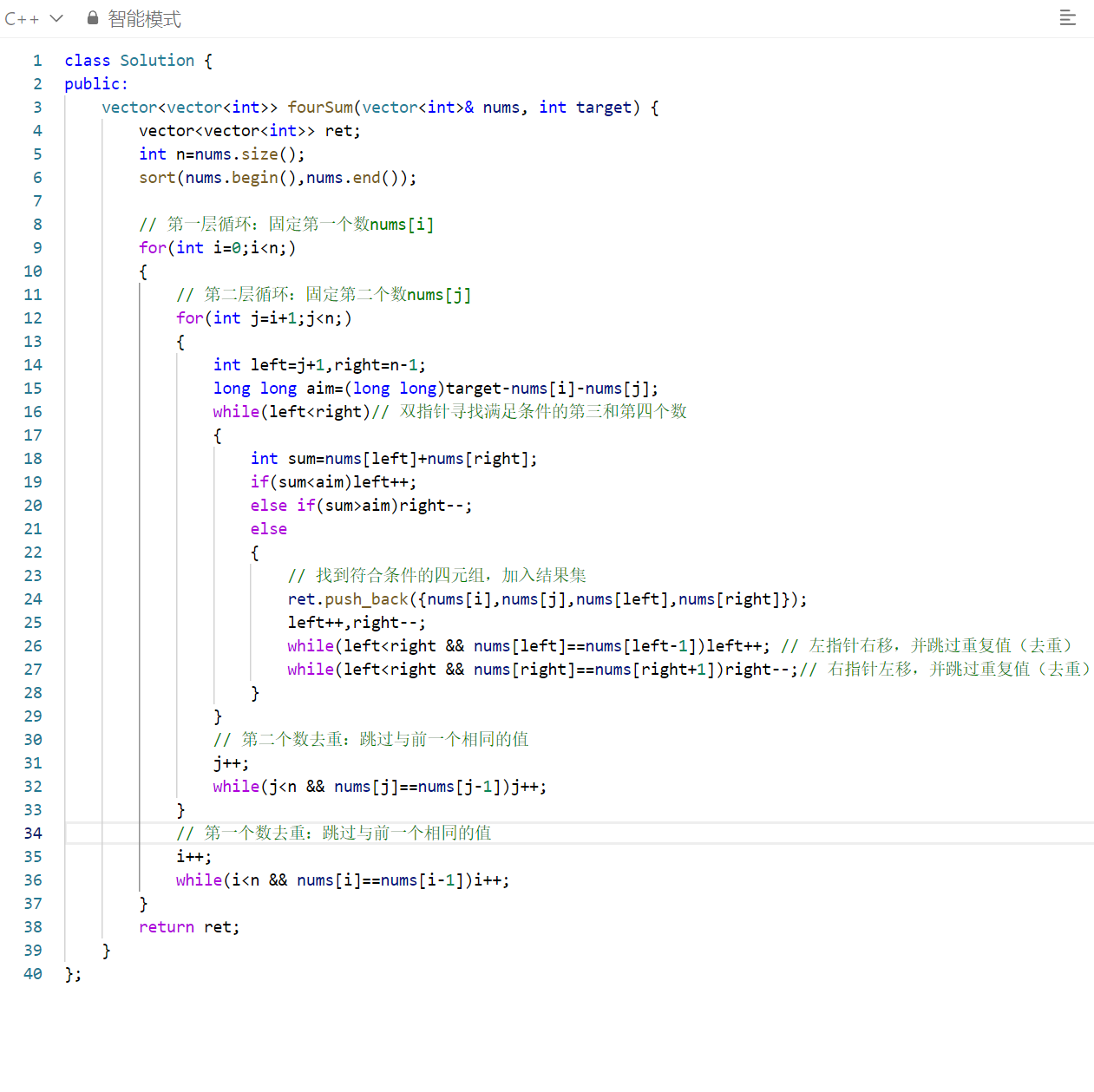
- 使用
long long类型存储四数之和,避免因整数过大导致的溢出错误 - 特别是当数组中存在较大的正数或较小的负数时,这个处理尤为重要
时间和空间复杂度
-
时间复杂度:O(n³)
- 排序:O (n log n)
- 两层外层循环:O (n²)
- 内层双指针循环:O (n)
- 总体由主导项 O (n³) 决定
-
空间复杂度:O (log n) 或 O (n)
- 取决于排序算法的实现,一般为 O (log n)
- 如果考虑存储结果的空间,则为 O (n)
