数据标准化与归一化的区别与应用场景
哈喽,我是我不是小upper!~
今儿和大家聊一个简单的话题:数据标准化与归一化的区别与应用场景。
好像很简单,但是为了更加的清晰,从各方面和大家详细的聊聊~
一、数据标准化(Standardization)
定义:通过线性变换将原始数据转换为均值为 0、标准差为 1 的分布,也称为 “Z - 分数标准化”(Z-Score Normalization)。
数学公式: 其中:
- x 是原始数据;
是该特征的均值(
);
是该特征的标准差(
)。
操作结果:
- 转换后的数据均值为 0,标准差为 1,分布形态与原始数据一致(仅位置和尺度变化);
- 数据范围通常落在[-3, 3]之间(因正态分布中约 99.7% 的数据在均值 ±3 倍标准差内),但无严格上下限;
- 保留了原始数据的分布特征(如偏态、峰值)和异常值的相对位置。
二、数据归一化(Normalization)
定义:通过线性变换将原始数据按比例缩放到指定的固定区间(最常用为[0, 1],少数场景为[-1, 1]),也称为 “Min-Max 缩放”。
数学公式(缩放至[0, 1]): 其中:
是该特征的最小值;
是该特征的最大值;
- 分母为数据的 “极差”(Range),反映数据的分布范围。
操作结果:
- 转换后的数据严格落在[0, 1]区间内,数值大小直接反映其在原始数据中的相对位置(如 x'=0.8表示该值处于原始范围的 80% 位置);
- 数据的比例关系被保留(如原始数据中a是b的 2 倍,归一化后仍保持 2 倍关系);
- 缩放范围由数据的最值决定,若存在极端值,大部分数据可能被压缩在狭小区间内。
三、标准化与归一化的核心对比
| 对比项 | 标准化(Standardization) | 归一化(Normalization) |
|---|---|---|
| 核心目标 | 将数据转换为均值 0、标准差 1 的分布,消除量纲影响 | 将数据缩放到固定区间(如\([0,1]\)),统一数值范围 |
| 公式参数 | 依赖均值( | 依赖最小值( |
| 结果分布 | 分布形态与原始数据一致,无严格上下限 | 强制落在固定区间,分布形态可能被压缩 |
| 量纲保留 | 失去原始物理意义(如 “温度” 转换后无单位) | 保留相对比例关系(如原始数据的 “倍数” 关系) |
四、适用场景与算法适配
特征缩放的选择需结合数据特性和算法原理,以下是具体场景的适配建议:
1. 优先选择标准化的场景
基于分布假设的算法:
- 主成分分析(PCA):依赖数据的协方差矩阵,标准化后各特征方差均为 1,避免方差大的特征主导主成分(如 “收入” 方差远大于 “年龄” 时,未标准化的 PCA 可能主要反映收入变化);
- 线性回归、逻辑回归:模型参数更新依赖梯度下降,标准化可使不同特征的梯度量级一致,加速收敛;同时,标准化后系数大小可直接反映特征重要性(因量纲统一)。
基于距离度量的算法:
- K 近邻(KNN)、K-Means:距离计算(如欧氏距离)对数值范围敏感,标准化可平衡不同量纲特征的权重(如 “身高(厘米)” 和 “体重(千克)” 需统一尺度后再计算距离);
- 支持向量机(SVM):核函数基于样本间相似度,标准化可避免数值大的特征(如 “收入”)对相似度计算的主导。
存在异常值的数据: 标准化对异常值更稳健(因标准差受异常值影响小于极差)。例如,包含极端高收入的数据集,标准化后大部分数据仍能保持分散,而归一化可能因极端值将多数数据压缩至接近 0 的区间。
2. 优先选择归一化的场景
对数值范围敏感的算法:
- 神经网络:输入层神经元的激活函数(如 Sigmoid)在[0,1] 区间内梯度更稳定,归一化可避免因输入值过大导致的梯度消失;
- 决策树以外的树模型:如梯度提升树(GBDT),虽然单棵树对量纲不敏感,但归一化可使特征的分裂阈值更易比较,提升集成效率。
需要保留相对比例的场景:
- 图像处理:像素值天然在 [0,255] 区间,归一化至[0,1]可保留像素的明暗比例,便于卷积操作;
- 推荐系统:用户评分(如 1-5 星)归一化后,可直接反映 “偏好强度” 的相对大小。
数据分布未知或非正态分布: 当数据不服从正态分布(如指数分布、均匀分布)时,归一化的固定区间更便于模型处理(如聚类时避免数据分布差异导致的簇偏移)。
五、优缺点分析
数据标准化的优缺点
优点:
- 对异常值稳健:相比归一化,受极端值影响更小(标准差对异常值的敏感度低于极差);
- 适配多数统计模型:满足 PCA、回归等算法对分布的假设,提升模型解释性(如标准化后的回归系数可直接比较);
- 保留数据分布特征:转换后的数据仍能反映原始数据的偏态、峰值等特性,适合需要分析分布规律的场景。
缺点:
- 失去物理意义:转换后的数据无实际单位(如 “年龄” 转换后的值无法对应具体岁数),不便于业务解读;
- 对非高斯分布效果有限:若原始数据是高度偏态分布(如收入数据),标准化后仍无法满足正态假设,可能影响依赖分布的算法(如线性回归)。
数据归一化的优缺点
优点:
- 数值范围明确:固定区间(如[0,1])便于调试模型参数(如神经网络的学习率);
- 保留相对比例:适合需要 “相对大小” 的场景(如推荐系统中用户对物品的偏好程度比较);
- 计算简单:仅需极值即可完成转换,无需遍历所有数据计算均值和标准差。
缺点:
- 对异常值敏感:极差受极端值影响大,如数据中存在一个极大值,多数样本可能被压缩至接近 0 的区间(如[0, 1000]中的数据,因一个值为 10000,归一化后多数数据接近 0);
- 适配场景有限:不适合依赖分布假设的算法(如 PCA),也不适合需要距离公平性的场景(如 KNN)。
完整案例
我们使用一个示例数据集,包含两个特征范围差异明显的列。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler, MinMaxScaler# 创建数据集
np.random.seed(42)
data = {"Feature1": np.random.randint(1, 100, 50), # 范围较大"Feature2": np.random.rand(50) * 10, # 范围较小
}
df = pd.DataFrame(data)# 原始数据分布
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.hist(df["Feature1"], bins=10, alpha=0.7, label="Feature1")
plt.hist(df["Feature2"], bins=10, alpha=0.7, label="Feature2")
plt.title("Original Data Distribution")
plt.legend()plt.subplot(1, 2, 2)
plt.boxplot([df["Feature1"], df["Feature2"]], labels=["Feature1", "Feature2"])
plt.title("Original Data Boxplot")
plt.show()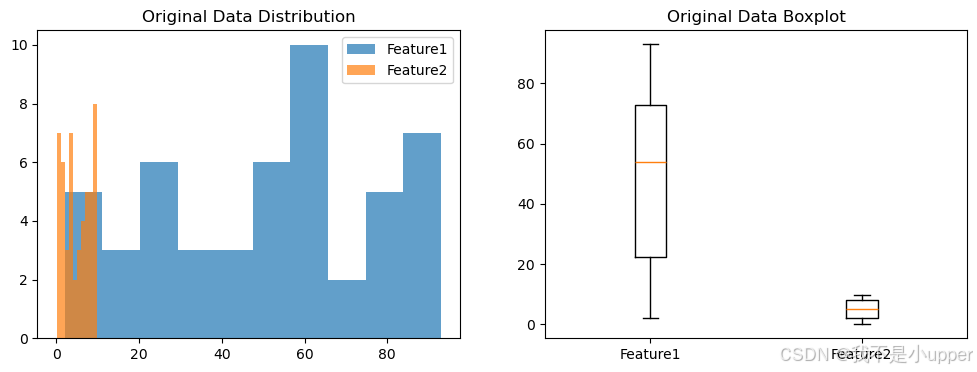
标准化与归一化实现
# 标准化
scaler_std = StandardScaler()
df_std = pd.DataFrame(scaler_std.fit_transform(df), columns=["Feature1", "Feature2"])# 归一化
scaler_norm = MinMaxScaler()
df_norm = pd.DataFrame(scaler_norm.fit_transform(df), columns=["Feature1", "Feature2"])# 可视化比较
plt.figure(figsize=(12, 6))# 标准化后的分布
plt.subplot(2, 2, 1)
plt.hist(df_std["Feature1"], bins=10, alpha=0.7, label="Feature1")
plt.hist(df_std["Feature2"], bins=10, alpha=0.7, label="Feature2")
plt.title("Standardized Data Distribution")
plt.legend()# 归一化后的分布
plt.subplot(2, 2, 2)
plt.hist(df_norm["Feature1"], bins=10, alpha=0.7, label="Feature1")
plt.hist(df_norm["Feature2"], bins=10, alpha=0.7, label="Feature2")
plt.title("Normalized Data Distribution")
plt.legend()# 标准化后的箱线图
plt.subplot(2, 2, 3)
plt.boxplot([df_std["Feature1"], df_std["Feature2"]], labels=["Feature1", "Feature2"])
plt.title("Standardized Data Boxplot")# 归一化后的箱线图
plt.subplot(2, 2, 4)
plt.boxplot([df_norm["Feature1"], df_norm["Feature2"]], labels=["Feature1", "Feature2"])
plt.title("Normalized Data Boxplot")
plt.show()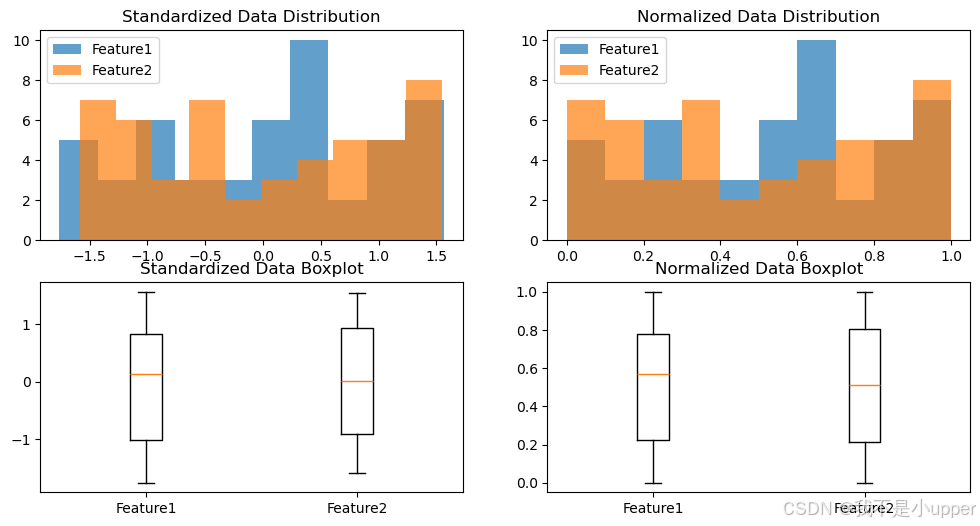
原始数据分布显示了两个特征的范围差异。
标准化后,数据呈现均值为 0,标准差为 1 的分布;归一化后,数据被压缩到 [0,1] 的区间。
总结一下:
异同点
共同点:两者都解决了不同量纲特征之间的权重不均问题。
不同点:标准化基于均值和标准差调整分布;归一化基于最大值和最小值调整范围。
选择建议
标准化:当算法对分布敏感或需要标准正态分布时(如 PCA、SVM、回归分析)。
归一化:当特征范围差异大,且需要固定区间范围时(如神经网络、梯度下降优化)。
