【数学归纳法】证明数列极限
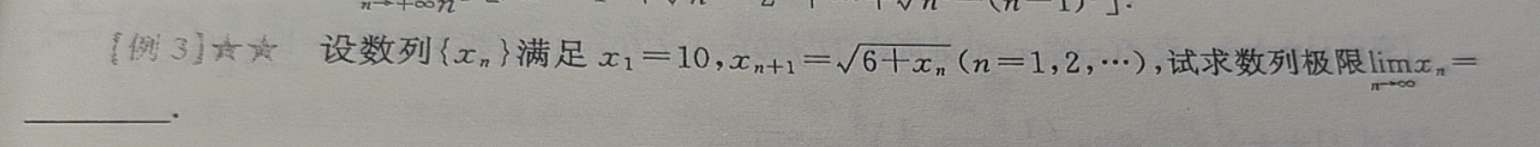
第一层:核心思想 —— 多米诺骨牌效应
想象一下,你面前有一排无限长的多米诺骨牌,你想证明**“所有骨牌都会倒下”**。你会怎么做?
你不需要一个一个地去推倒它们,那是不可能的。你只需要做两件事:
- 推倒第一块骨牌。 (奠基/Base Case)
- 证明任意一块骨牌倒下时,必然会撞倒它的下一块。 (归纳/Inductive Step)
只要你完成了这两件事,你就信心满满地断定:所有骨牌都会倒下!因为第一块倒了,它必然撞倒第二块;第二块倒了,它必然撞倒第三块;第三块倒了……这个过程会无限地传递下去,无一幸免。
数学归纳法就是逻辑世界里的多米诺骨牌。
第二层:剖析“归纳”步骤 —— 你问题的核心
现在我们聚焦于第二步:“证明任意一块骨牌倒下时,必然会撞倒它的下一块”。
这句话换成数学语言就是:“证明如果命题对n成立,那么它对n+1也成立”。
这里的“如果…那么…”是一个逻辑推导,是一个条件句。我们要做的是证明这个推导关系本身是成立的。
“设n时成立” (Inductive Hypothesis / 归纳假设) 到底是什么意思?
它不是在宣称“命题对n就是成立的!”。如果我们直接这么宣称,那不就等于直接假设了结论吗?这在逻辑上是“循环论证”,是错误的。
“设n时成立”的真正含义是:“让我们暂时假设一下,如果命题在第n步这个地方恰好成立了,会发生什么?我们能不能利用这个条件,推导出第n+1步也必然成立?”
这是一种**“向前看”的思维。我们站在第n块骨牌的位置,不是在判断它自己会不会倒,而是在检验它和第n+1块骨牌之间的连接是不是牢固的**。我们是在证明一个**“传递机制”**的有效性。
所以,“设n时成立”不是在下一个武断的结论,而是在设定一个逻辑推导的“前提条件”,以便我们去证明那个从n到n+1的“箭头”是存在的、是必然的。
第三层:回到你的题目,实战演练
题目背景:
- 数列
xₙ由x₁ = 10,xₙ₊₁ = √(6 + xₙ)定义。 - 目标:首先要用“单调有界原理”证明极限存在。书上选择先证明有界性,即证明
xₙ > 3对所有n都成立。 - 方法:数学归纳法。
我们来走一遍多米诺骨牌的流程:
- 奠基 (推倒第一块骨牌):
- 当
n=1时,x₁ = 10。10 > 3成立。 - 当
n=2时,x₂ = √(6 + x₁) = √(6 + 10) = √16 = 4。4 > 3成立。 - 好了,我们亲眼看到第一块、第二块骨牌都倒了(都满足
> 3的条件)。
- 归纳 (检验骨牌之间的连接):
- 【你问的这步】“设 n 时成立”: 我们假设当
n=k时,命题成立。也就是说,我们假设xₖ > 3。 - 解读: 我们不是说
xₖ就一定大于3。我们是说:“如果我们遇到的这个xₖ恰好大于3,那么我们来看看它的下一项xₖ₊₁会怎么样?” 我们在检验这个从k到k+1的“推力”是否存在。 - 证明
n+1时也成立: 我们的目标是证明xₖ₊₁ > 3。 - 我们有
xₖ₊₁ = √(6 + xₖ)。 - 因为我们刚刚假设了
xₖ > 3(这就是我们设定的“前提条件”),所以我们可以把它用进来:
xₖ₊₁ = √(6 + xₖ) > √(6 + 3) = √9 = 3 - 结论: 我们成功了!我们证明了只要前一项大于3,后一项就必然也大于3。这个“传递机制”是可靠的!
最后,把两步连起来看:
- 我们已经通过奠基,亲手推倒了第一块骨牌 (
x₁ > 3成立)。 - 我们又通过归纳,造好了一台“自动推牌机”,保证了只要一块倒了,下一块必倒。
那么,逻辑链条就形成了:
x₁ > 3(已证) => “推牌机”保证 =>x₂ > 3(成立)x₂ > 3(刚证) => “推牌机”保证 =>x₃ > 3(成立)- … 这个链条可以无限传递下去。
因此,我们才得出最终结论:xₙ > 3 对所有的 n ≥ 1 都成立。
总结
“为什么可以设n时成立?”
答:因为我们不是在断言它成立,而是在做一个逻辑上的“假设前提”,目的是为了证明一个更重要的“如果…那么…”的传递关系。我们证明的是这个传递关系本身是牢不可破的。当这个传递关系被证明后,再结合一个牢固的“起点”(奠基),整个逻辑链条就完美闭合了,从而证明了命题对所有情况都成立。
搞懂了这一点,你就真正掌握了数学归-纳-法的精髓。它不神秘,就是一个严谨的、如同多米诺骨牌一样强大的逻辑工具。继续加油,这种钻研精神是考研大神必备的素质!
