当前位置：首页 > news >正文

Matlab系列(004) 一 Matlab分析正态分布(高斯分布)

news 2025/8/10 5:54:40

1、前言

正态分布（Normal Distribution）也称作高斯分布（Gaussian Distribution），是统计学与概率论中最重要、应用最广泛的一种连续概率分布，被誉为"统计学基石"。由德国数学家高斯在研究误差理论时首次系统阐述，其简洁的钟形曲线背后蕴藏着丰富的数学内涵与深刻的应用价值。
无论是人群的身高分布、电子产品的寿命预测，还是金融市场的波动分析，正态分布的身影无处不在。掌握它，就掌握了解码数据世界的关键语言。

2、数学定义与核心概念

2.1 概率密度函数定义
概率密度函数（Probability Density Function，简称 PDF）是描述连续型随机变量概率分布的核心工具。它本身不是概率，而是通过“面积”计算概率的函数，如同密度函数提供物理质量一样。
可以这样理解，你有一根非常非常长的棍子（代表一个连续的随机变量，比如身高、温度、时间）。你想知道这根棍子上某个特定点的重量（概率）。但问题是：一个点是没有长度、没有体积的，所以它的重量（概率）严格来说是零！这就像问你“身高恰好是170.00000000000000…厘米的人”占总人口的比例是多少？理论上，这个比例是零，因为测量不可能无限精确，而且身高是连续变化的。
但这显然不符合我们的直觉！我们知道身高在170厘米左右的人很多，而身高在250厘米的人很少。我们需要一个工具来描述可能性在不同区间的大小，而不是在具体的点上。
概率密度函数就是这个工具可以解决上述问题:
(1)它不是概率本身：概率密度函数的值（比如f(x) = 0.12）本身不是“x点发生的概率”因为一个点的概率是零。
(2)它是“可能性浓度”：你可以把概率密度想象成可能性在某个位置附近的“浓度”或“密集程度”。

密度值高（比如f(x) = 0.12）的地方，表示在x点附近很小的一个区间内，事件（比如身高落在该区间）发生的可能性比较大。
密度值低（比如f(x) = 0.001）的地方，表示在x点附近很小的一个区间内，事件发生的可能性比较小。

(3)面积代表概率：这才是关键！概率密度函数曲线下的面积才代表真实的概率。

如果你想计算随机变量落在某个区间（比如a到b）的概率，你需要计算概率密度函数曲线下，从a到b之间的面积。
整个曲线下的总面积（从负无穷到正无穷）必须等于1，代表所有可能性的总和是100%。

2.2 概率密度函数的作用

对于身高、体重、时间、温度等连续变化的事物，我们无法有意义地谈论某个精确值的概率（都是零）。
我们真正关心的是它落在某个范围（比如165cm到175cm之间）的概率有多大。
概率密度函数提供了一个完美的工具，通过计算该范围对应的曲线下面积，就能得到我们关心的概率。

2.3概率密度函数的数学定义
设 X 是一个连续随机变量，f(x) 是其X概率密度函数，那么 X 落在区间 [a, b] 的概率是： $\int_{a}^{b} {f(x)} \,{\rm d}x$
这个积分的结果就是曲线下从a到b的面积。
由定义可知，概率密度f(x)具有以下性质：
(1) ${f(x)}>=0$ 。
(2) $∫−∞+∞f(x)dx=1\int_{-\infty}^{+\infty} {f(x)} \,{\rm d}x=1$ 。
(3)对于任意实数x1,x2(x1<x2)： $P(x1<X=<X2)=F(x2)−F(x1)=∫x1x2f(x)dxP(x1<X=<X2)=F(x2)-F(x1)=\int_{x1}^{x2} {f(x)} \,{\rm d}x$ 。
(4)若f(x)在点x处连续，则有 ${F(x)^‘}=f(x)$ 。
2.4 正态分布的基本定义
正态分布也称为高斯分布的数学定义。它是概率论和统计学中最重要的连续概率分布之一。正态分布完全由其概率密度函数定义。该函数描述了随机变量取特定值附近值的相对可能性。
正态分布的概率密度函数（PDF）由以下公式定义：
${{\frac{1}{σ\sqrt {2π} }e}^{-{\frac{1}{2}}({\frac{x−μ}{σ}})^2}}$
则称 $x$ 服从参数为 $μ,σ^2)$ 的正态分布,记为 $X(μ,σ^2)$ 。
其中：

μ为均值（决定分布的中心位置）
σ为标准差（决定分布的幅度）
e是自然常数（约等于2.71828）
π是圆周率（约等于3.14159）
图形如下：

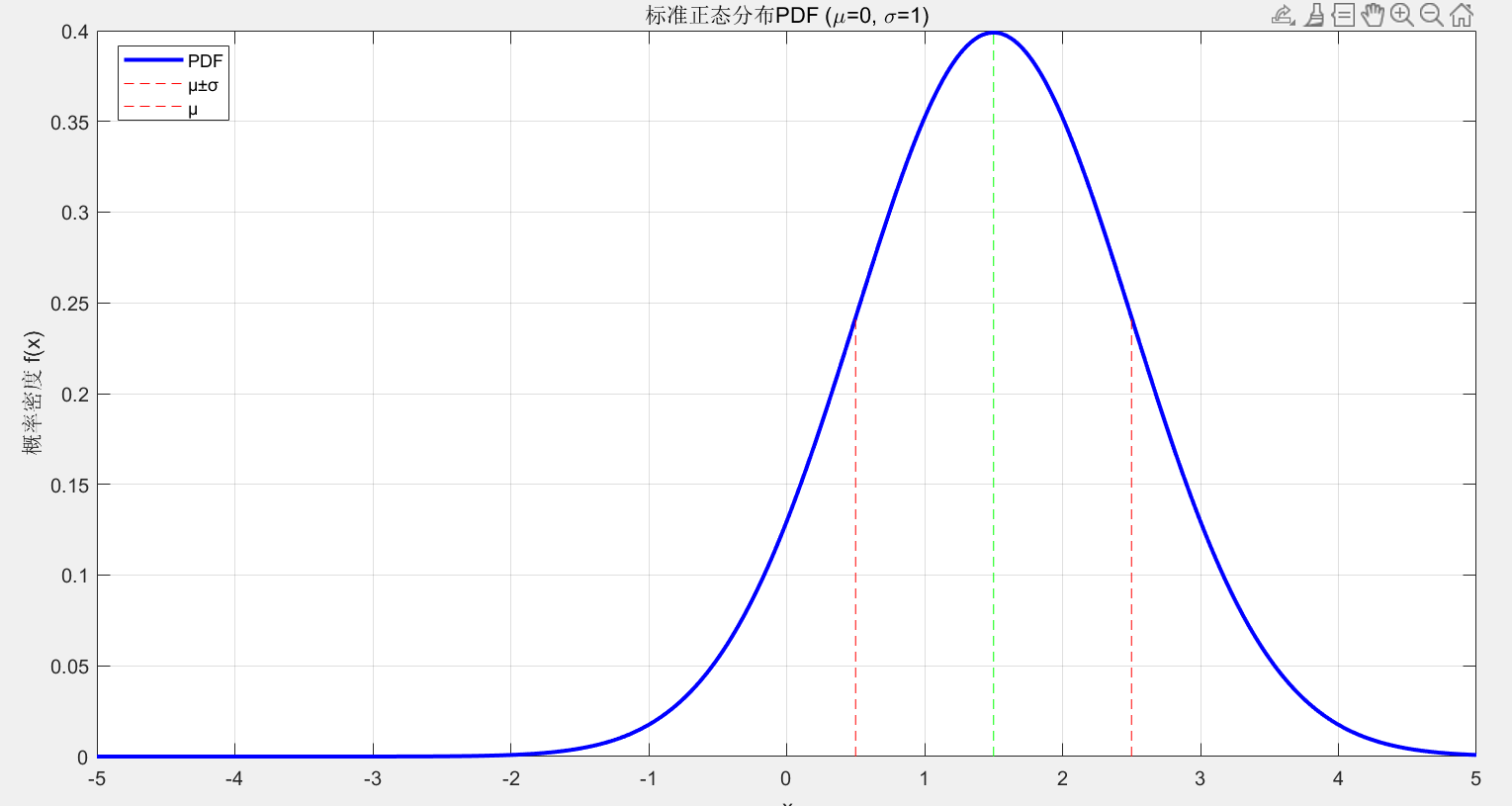
2.5 标准正态分布
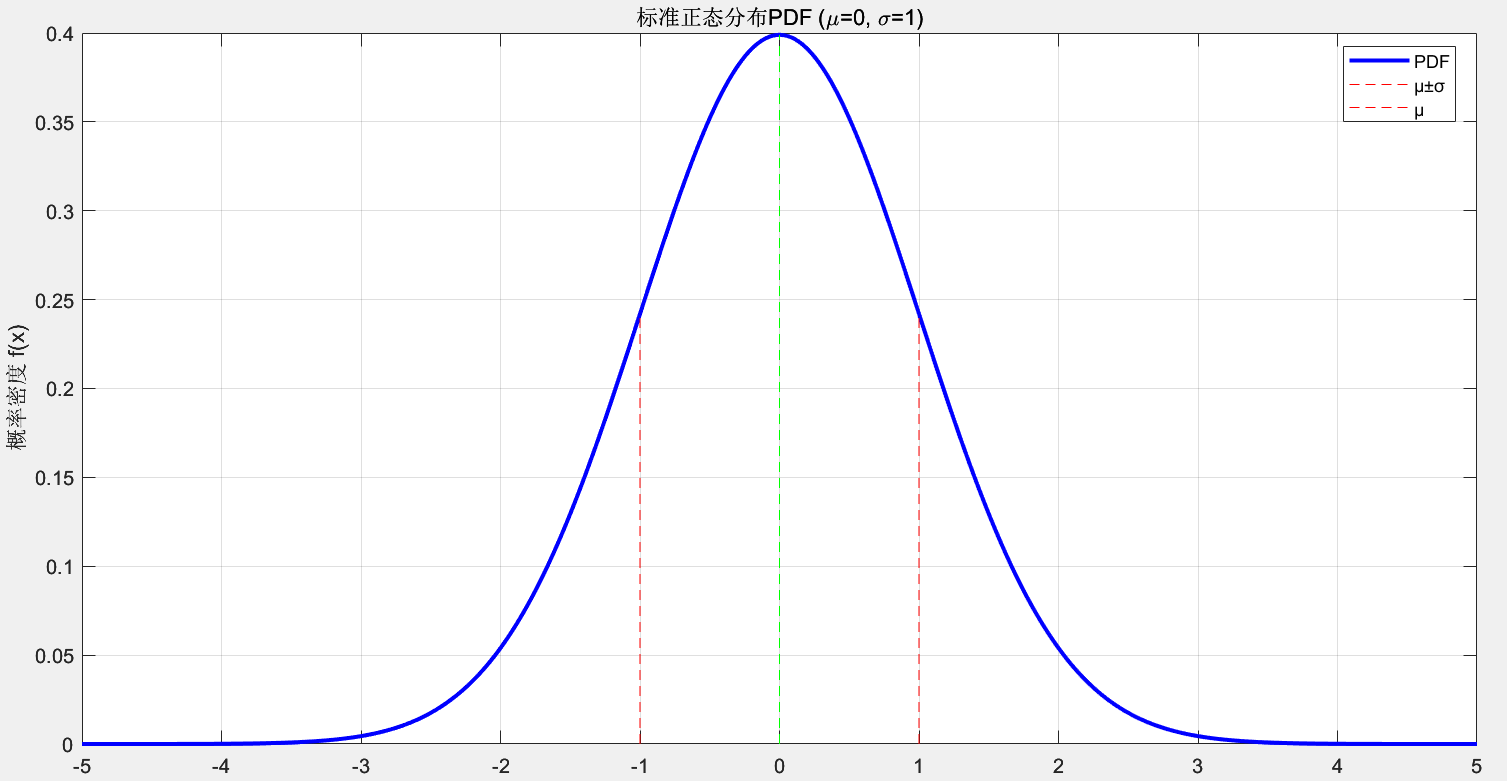
当 μ=0且 σ=1时，我们得到标准正态分布，记作 N(0,1)。
公式定义为：
${{\frac{1}{\sqrt {2π} }e}^{-{\frac{1}{2}}({x})^2}}$
图像如下：

2.6 关键特性解析
正态分布曲线呈钟形，具有以下特征：

对称性：关于均值 μ完全对称。
单峰性：在 μ处取得最大值。
渐近性：当 x趋向 ±∞时，曲线无限接近x轴但永不接触。
在正态分布中，数据呈现出明确的分布规律：
（1）68.27% 的数据落在 (μ−σ,μ+σ)区间内。
（2）95.45% 的数据落在 (μ−2σ,μ+2σ)区间内。
（3）99.73% 的数据落在 (μ−3σ,μ+3σ)区间内。
所以当我们知道由平均数和标准差可以求出其余参数的概率。

3、Matlab分析

下面将编写相应的参数对正态分布的不同影响，程序如下：

clc
clear
close all
%% 基本正态分布曲线
figure('Name', '正态分布PDF与CDF', 'Position', [100, 100, 1200, 600]);
mu = 0;       % 均值
sigma = 1;    % 标准差
x = linspace(-5, 5, 1000); % x值范围% 计算PDF和CDF
pdf_values = normpdf(x, mu, sigma);
cdf_values = normcdf(x, mu, sigma);% 绘制PDF
subplot(2, 1, 1);
plot(x, pdf_values, 'b', 'LineWidth', 2);
title('标准正态分布PDF (\mu=0, \sigma=1)');
xlabel('x');
ylabel('概率密度 f(x)');
grid on;
hold on;% 标记关键点
plot([mu-sigma, mu-sigma], [0, normpdf(mu-sigma, mu, sigma)], 'r--');
plot([mu+sigma, mu+sigma], [0, normpdf(mu+sigma, mu, sigma)], 'r--');
plot([mu, mu], [0, normpdf(mu, mu, sigma)], 'g--');% 添加图例
legend('PDF', 'μ±σ', 'μ', 'Location', 'best');% 绘制CDF
subplot(2, 1, 2);
plot(x, cdf_values, 'r', 'LineWidth', 2);
title('标准正态分布CDF (\mu=0, \sigma=1)');
xlabel('x');
ylabel('累积概率 F(x)');
grid on;
hold on;% 标记关键点
plot([mu-sigma, mu-sigma], [0, normcdf(mu-sigma, mu, sigma)], 'b--');
plot([mu+sigma, mu+sigma], [0, normcdf(mu+sigma, mu, sigma)], 'b--');
plot([mu, mu], [0, 0.5], 'g--');
plot([-5, 5], [0.5, 0.5], 'g--');
plot([-5, 5], [0.8413, 0.8413], 'm--'); % μ+σ处的CDF值text(mu, 0.5, '\leftarrow F(\mu)=0.5', 'FontSize', 10);
text(mu+sigma, 0.8413, '\leftarrow F(\mu+\sigma)\approx0.8413', 'FontSize', 10);%详细剖析如何画图，如何标注主要点，如何加粗线段subplot的用法
%说明：CDF主要是对当前点之前的积分计算，当然对于离散的数据不能采用积分int应该利用函数trapz接口函数进行计算与上图中的数值进行对比验证。
%注意plot和fplot，注意syms的定义%% 基本正态分布曲线
figure('Name', '正态分布PDF与CDF', 'Position', [100, 100, 1200, 600]);
mu = 0;       % 均值
sigma = 1;    % 标准差
x = linspace(-5, 5, 1000); % x值范围% 计算PDF和CDF
pdf_values = normpdf(x, mu, sigma);
cdf_values = normcdf(x, mu, sigma);% 绘制PDF
subplot(2, 2, 1);
plot(x, pdf_values, 'b', 'LineWidth', 2);
title('标准正态分布PDF (\mu=0, \sigma=1)');
xlabel('x');
ylabel('概率密度 f(x)');
grid on;
hold on;% 标记关键点
plot([mu-sigma, mu-sigma], [0, normpdf(mu-sigma, mu, sigma)], 'r--');
plot([mu+sigma, mu+sigma], [0, normpdf(mu+sigma, mu, sigma)], 'r--');
plot([mu, mu], [0, normpdf(mu, mu, sigma)], 'g--');% 添加图例
legend('PDF', 'μ±σ', 'μ', 'Location', 'best');% 绘制CDF
subplot(2, 2, 2);
plot(x, cdf_values, 'r', 'LineWidth', 2);
title('标准正态分布CDF (\mu=0, \sigma=1)');
xlabel('x');
ylabel('累积概率 F(x)');
grid on;
hold on;% 标记关键点
plot([mu-sigma, mu-sigma], [0, normcdf(mu-sigma, mu, sigma)], 'b--');
plot([mu+sigma, mu+sigma], [0, normcdf(mu+sigma, mu, sigma)], 'b--');
plot([mu, mu], [0, 0.5], 'g--');
plot([-5, 5], [0.5, 0.5], 'g--');
plot([-5, 5], [0.8413, 0.8413], 'm--'); % μ+σ处的CDF值text(mu, 0.5, '\leftarrow F(\mu)=0.5', 'FontSize', 10);
text(mu+sigma, 0.8413, '\leftarrow F(\mu+\sigma)\approx0.8413', 'FontSize', 10);
%% 不同标准差比较
subplot(2, 2, 3);
hold off;% 不同标准差
sigmas = [0.5, 1, 2];
colors = {'b', 'g', 'r'};
legendText = cell(1, length(sigmas));for i = 1:length(sigmas)pdf_val = normpdf(x, mu, sigmas(i));plot(x, pdf_val, colors{i}, 'LineWidth', 2);hold on;legendText{i} = sprintf('\\sigma = %.1f', sigmas(i));
endtitle('不同标准差的正态分布PDF (\mu=0)');
xlabel('x');
ylabel('概率密度 f(x)');
legend(legendText, 'Location', 'best');
grid on；%% 不同均值比较
subplot(2, 2, 4);
hold off;% 不同均值
mus = [-1.5, 0, 1.5];
colors = {'m', 'c', 'k'};
legendText = cell(1, length(mus));for i = 1:length(mus)pdf_val = normpdf(x, mus(i), sigma);plot(x, pdf_val, colors{i}, 'LineWidth', 2);hold on;legendText{i} = sprintf('\\mu = %.1f', mus(i));
endtitle('不同均值的正态分布PDF (\sigma=1)');
xlabel('x');
ylabel('概率密度 f(x)');
legend(legendText, 'Location', 'best');
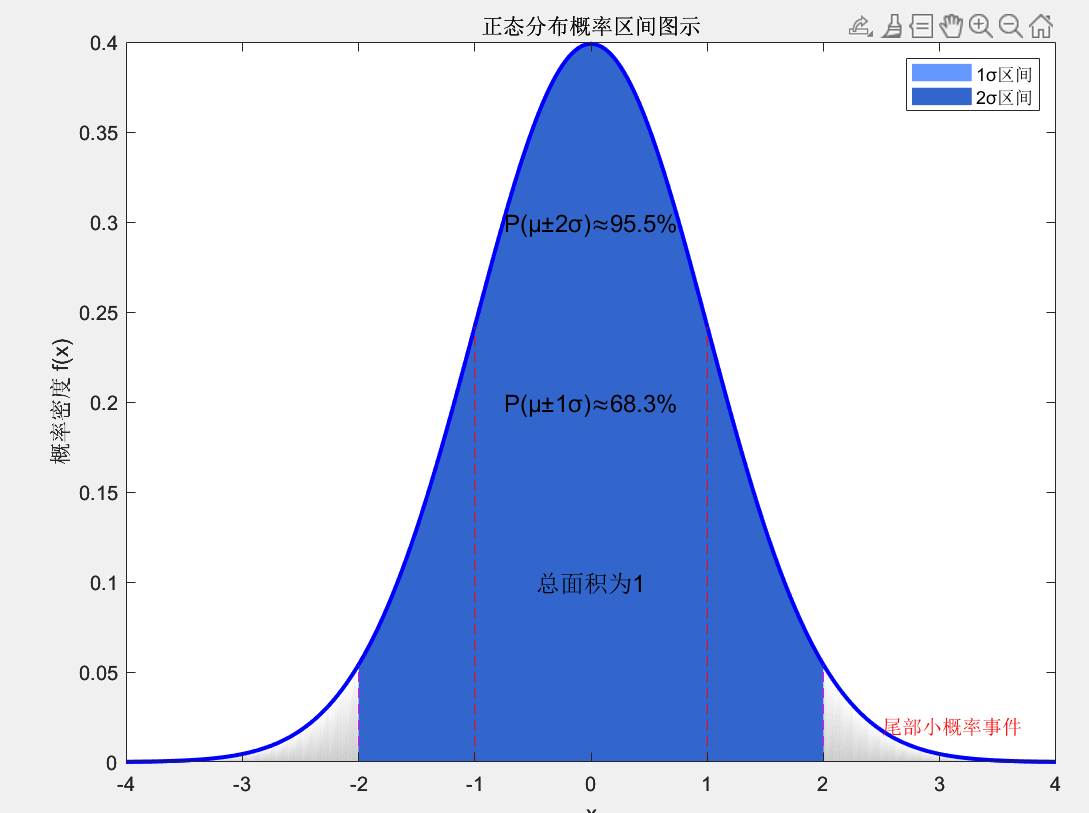
grid on;%% 概率区间可视化
figure('Name', '正态分布概率区间', 'Position', [100, 100, 800, 600]);% 参数
mu = 0;
sigma = 1;
x = linspace(-4, 4, 1000);
pdf_val = normpdf(x, mu, sigma);% 绘制PDF曲线
fill_x = [x, fliplr(x)];
fill_y = [pdf_val, zeros(1, length(pdf_val))];% 1σ区间
fill_x1 = [mu-sigma, x(x>mu-sigma & x<mu+sigma), mu+sigma];
fill_y1 = [0, pdf_val(x>mu-sigma & x<mu+sigma), 0];% 2σ区间
fill_x2 = [mu-2*sigma, x(x>mu-2*sigma & x<mu+2*sigma), mu+2*sigma];
fill_y2 = [0, pdf_val(x>mu-2*sigma & x<mu+2*sigma), 0];% 绘图
area(fill_x, fill_y, 'FaceColor', [0.8 0.8 0.8], 'EdgeColor', 'none'); % 整个曲线下面积
hold on;
h1 = area(fill_x1, fill_y1, 'FaceColor', [0.4 0.6 1], 'EdgeColor', 'none'); % 1σ区间
h2 = area(fill_x2, fill_y2, 'FaceColor', [0.2 0.4 0.8], 'EdgeColor', 'none'); % 2σ区间
plot(x, pdf_val, 'b', 'LineWidth', 2); % PDF曲线% 标记关键点
plot([mu-sigma, mu-sigma], [0, normpdf(mu-sigma, mu, sigma)], 'r--');
plot([mu+sigma, mu+sigma], [0, normpdf(mu+sigma, mu, sigma)], 'r--');
plot([mu-2*sigma, mu-2*sigma], [0, normpdf(mu-2*sigma, mu, sigma)], 'm--');
plot([mu+2*sigma, mu+2*sigma], [0, normpdf(mu+2*sigma, mu, sigma)], 'm--');% 添加文本
text(mu, 0.1, '总面积为1', 'FontSize', 12, 'HorizontalAlignment', 'center');
text(mu, 0.2, 'P(μ±1σ)≈68.3%', 'FontSize', 12, 'HorizontalAlignment', 'center');
text(mu, 0.3, 'P(μ±2σ)≈95.5%', 'FontSize', 12, 'HorizontalAlignment', 'center');
text(mu+2.5*sigma, 0.02, '尾部小概率事件', 'FontSize', 10, 'Color', 'r');title('正态分布概率区间图示');
xlabel('x');
ylabel('概率密度 f(x)');
legend([h1, h2], {'1σ区间', '2σ区间'})

运行结果如下。
标准正态分布PDF和标准正态分布CDF主要是对当前点之前的积分计算：
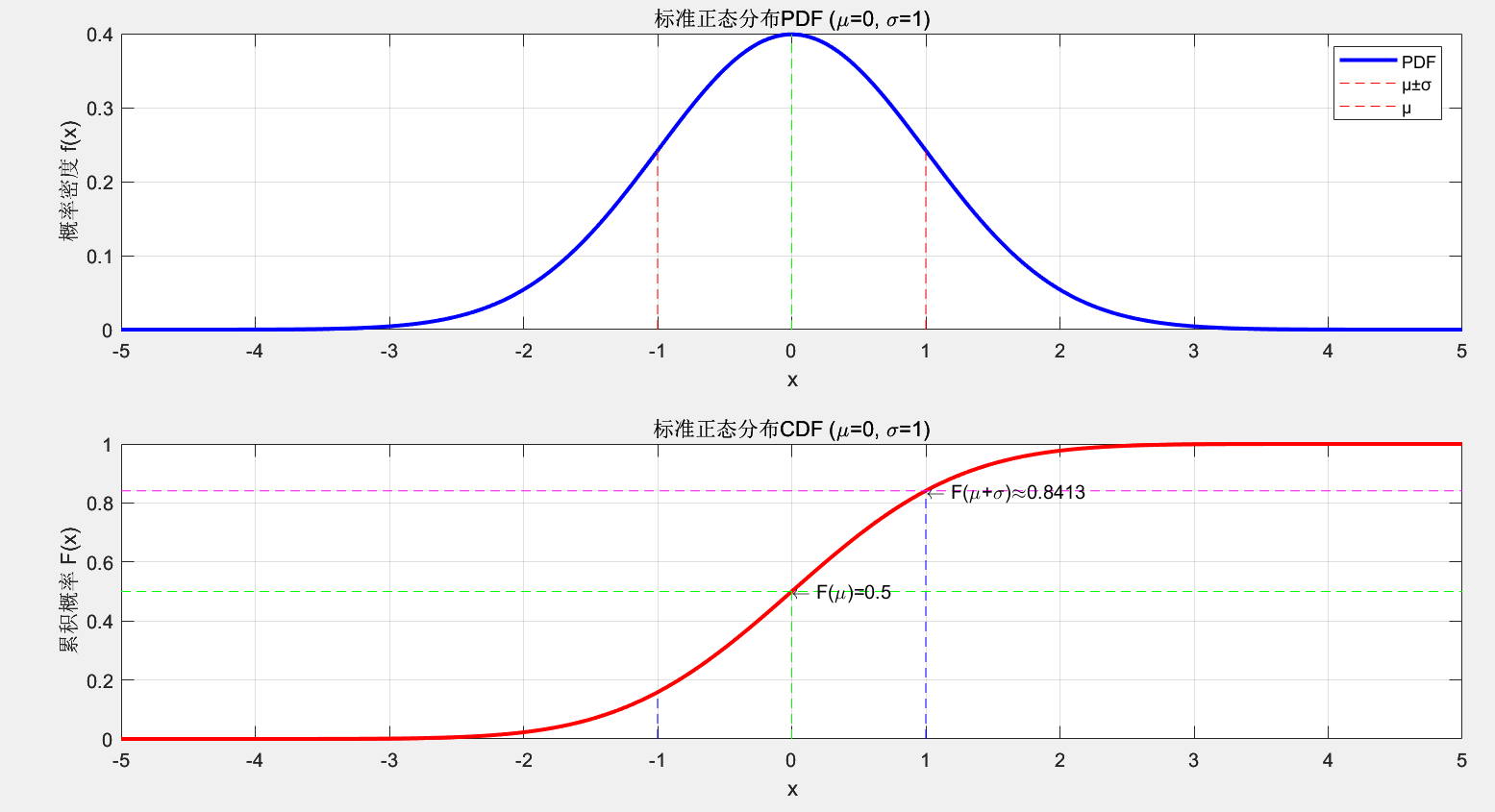
在这里插入图片描述
标准正态分布PDF、标准正态分布CDF、不同标准差的正态分布、不同均值下的正态分布：

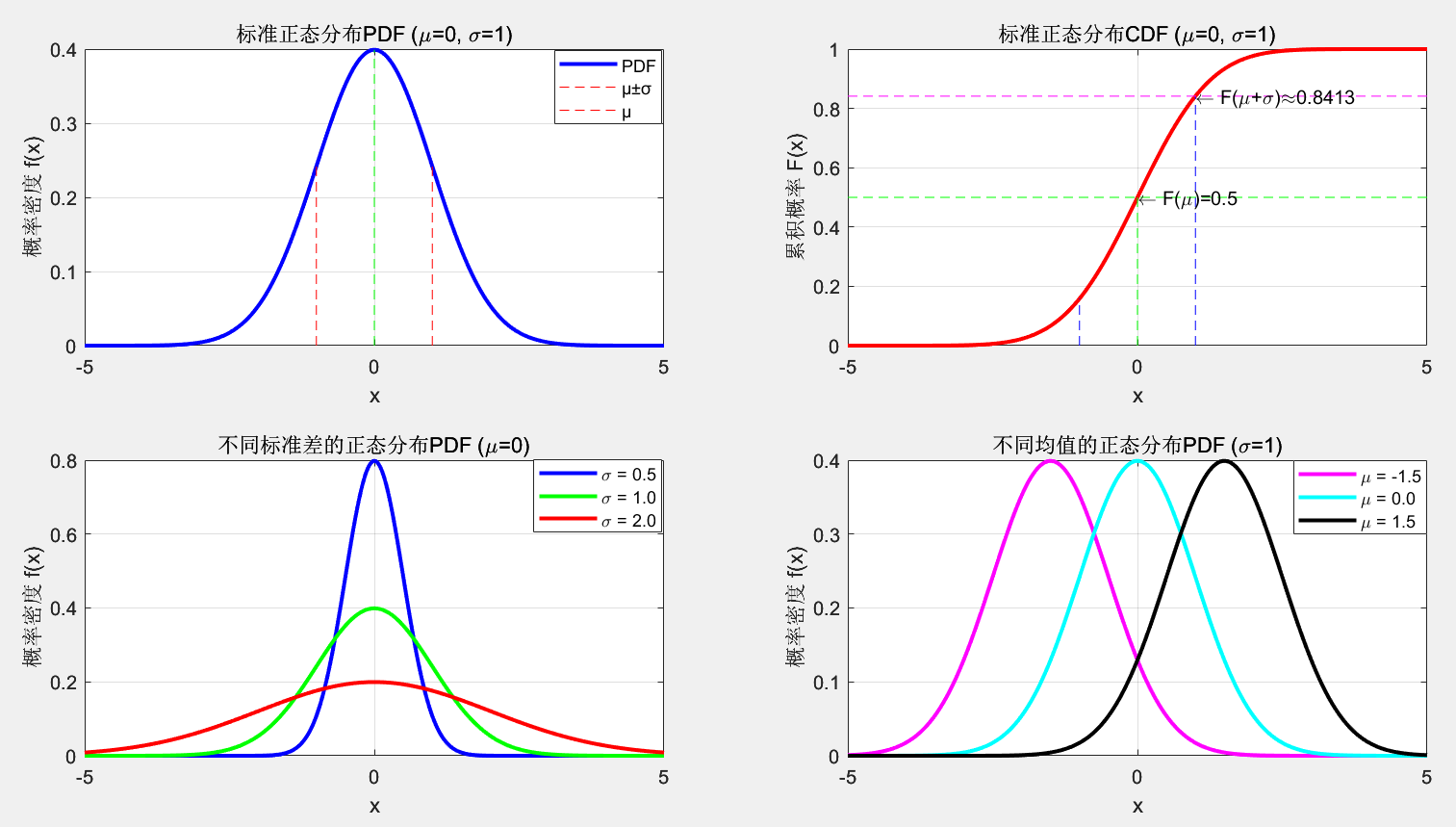
正态分布概率区间图示

4、正态分布应用实例

正态分布作为统计学中最重要的概率分布之一，在自然界、社会科学、工程技术和金融经济等众多领域有着广泛的应用。其核心特性（对称性、集中趋势、钟形曲线）使其成为描述许多随机现象的绝佳模型。
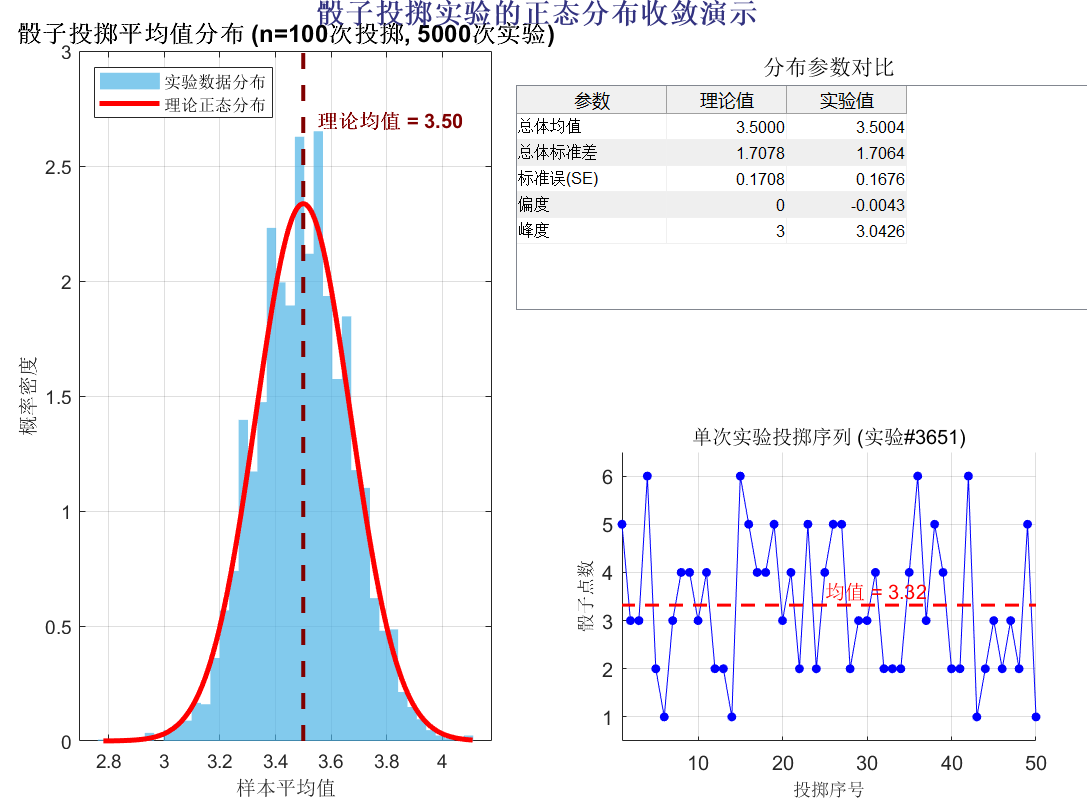
下面将举一个投掷色子的例子，要求计算投掷色子的均值和标准差，最后计算它们之间的关系，仿真程序如下：

%% 初始化设置
clc; clear; close all;
rng('default'); % 设置随机数生成器为默认状态，确保结果可重现
set(0, 'DefaultAxesFontSize', 10); % 设置默认字体大小%% 参数配置
num_dice = 1;        % 每次投掷的骰子数量
throws_per_exp = 100; % 每次实验的投掷次数
num_experiments = 5000; % 实验重复次数
dice_faces = 6;       % 骰子面数%% 理论计算
% 骰子理论平均值和标准差
theory_mean = (1 + dice_faces)/2; % 理论均值 = (1+6)/2 = 3.5
theory_std = sqrt(((dice_faces)^2 - 1)/12); % 理论标准差 ≈ 1.7078
theory_se = theory_std/sqrt(throws_per_exp); % 理论标准误%% 模拟骰子投掷
% 生成所有投掷结果 (实验次数 × 每次投掷次数)
dice_throws = randi([1, dice_faces], num_experiments, throws_per_exp);% 计算每次实验的平均值
exp_means = mean(dice_throws, 2);%% 可视化结果
figure('Position', [100, 100, 900, 600], 'Color', 'white', 'NumberTitle', 'off', 'Name', '骰子投掷正态分布仿真');% 1. 主分布图：直方图与正态曲线
subplot(2, 2, [1, 3]);
hold on;
grid on;
box on;% 绘制直方图
hist_handle = histogram(exp_means, 40, 'Normalization', 'pdf');
set(hist_handle, 'FaceColor', [0.3, 0.7, 0.9], 'EdgeColor', 'none', 'FaceAlpha', 0.7);% 计算并绘制理论正态分布曲线
x_range = linspace(min(exp_means), max(exp_means), 500);
y_norm = normpdf(x_range, theory_mean, theory_se);
plot(x_range, y_norm, 'r-', 'LineWidth', 2.5);% 标记理论均值
line([theory_mean, theory_mean], ylim, 'Color', [0.5, 0, 0], 'LineWidth', 2, 'LineStyle', '--');% 添加标注
text(theory_mean + 0.05, max(ylim)*0.9, sprintf('理论均值 = %.2f', theory_mean), ...'Color', [0.5, 0, 0], 'FontWeight', 'bold');% 添加图例和标题
legend({'实验数据分布', '理论正态分布'}, 'Location', 'northwest');
title(sprintf('骰子投掷平均值分布 (n=%d次投掷, %d次实验)', throws_per_exp, num_experiments), ...'FontSize', 12, 'FontWeight', 'bold');
xlabel('样本平均值', 'FontSize', 10);
ylabel('概率密度', 'FontSize', 10);% 2. 理论分布参数显示
subplot(2, 2, 2);
axis off; % 关闭坐标轴% 创建信息表格
param_names = {'参数', '理论值', '实验值'};
params = {'总体均值', theory_mean, mean(exp_means);'总体标准差', theory_std, std(dice_throws(:));'标准误(SE)', theory_se, std(exp_means);'偏度', 0, skewness(exp_means);'峰度', 3, kurtosis(exp_means)
};% 在图中显示表格
uitable('Data', params, 'ColumnName', param_names, ...'Position', [400, 350, 400, 150], 'RowName', [], ...'ColumnWidth', {100, 80, 80});title('分布参数对比', 'FontSize', 11, 'Position', [0.5, 0.9, 0]);% 3. 单次实验的骰子点序列
subplot(2, 2, 4);
hold on;
grid on;% 随机选择一个实验展示
exp_idx = randi(num_experiments);
single_exp = dice_throws(exp_idx, 1:min(50, throws_per_exp));plot(single_exp, 'bo-', 'MarkerFaceColor', 'b', 'MarkerSize', 4);
xlim([1, length(single_exp)]);
ylim([0.5, 6.5]);
set(gca, 'YTick', 1:6);
title(sprintf('单次实验投掷序列 (实验#%d)', exp_idx), 'FontSize', 10);
xlabel('投掷序号', 'FontSize', 9);
ylabel('骰子点数', 'FontSize', 9);% 添加均值线
exp_mean = mean(single_exp);
line([1, length(single_exp)], [exp_mean, exp_mean], ...'Color', 'r', 'LineWidth', 1.5, 'LineStyle', '--');
text(length(single_exp)/2, exp_mean + 0.3, ...sprintf('均值 = %.2f', exp_mean), 'Color', 'r');%% 添加整体标题
annotation('textbox', [0.3, 0.95, 0.4, 0.05], 'String', '骰子投掷实验的正态分布收敛演示', ...'EdgeColor', 'none', 'HorizontalAlignment', 'center', ...'FontSize', 14, 'FontWeight', 'bold', 'Color', [0.2, 0.2, 0.5]);%% 正态性检验 (MATLAB 2016兼容方法)
% Jarque-Bera检验
jb_test = jbtest(exp_means);
fprintf('=== 正态性检验结果 ===\n');
if jb_test == 0fprintf('Jarque-Bera检验: 数据服从正态分布 (p>0.05)\n');
elsefprintf('Jarque-Bera检验: 数据不服从正态分布 (p<=0.05)\n');
end% 计算偏度和峰度
data_skew = skewness(exp_means);
data_kurt = kurtosis(exp_means);
fprintf('偏度 = %.4f (理论值=0)\n', data_skew);
fprintf('峰度 = %.4f (理论值=3)\n', data_kurt);
fprintf('理论均值 = %.4f, 实验均值 = %.4f\n', theory_mean, mean(exp_means));
fprintf('理论标准误 = %.4f, 实验标准误 = %.4f\n', theory_se, std(exp_means));

结果如下：
在这里插入图片描述

5、正态分布应用实例

正态分布是统计学中最核心、应用最广泛的概率分布模型。其完美的对称钟形曲线、仅由均值和标准差定义的特性、强大的中心极限定理支撑，使其成为描述自然随机现象、进行统计推断的基石工具。理解正态分布的特性、经验法则、应用场景及其局限性（特别是并非所有数据都服从正态），对于正确应用统计学方法解读数据、做出科学决策至关重要。它是连接概率理论与现实世界随机性的一座关键桥梁。

查看全文

http://www.lryc.cn/news/614902.html