当前位置：首页 > news >正文

代码随想录算法训练营 Day20

news 2025/8/8 15:10:20

LeetCode 39. 组合总和

链接：39. 组合总和 - 力扣（LeetCode）

思路：

回溯法：先把回溯法的模板写出来，再一步步考虑终止条件和剪枝。回溯的终止比较好想：当路径和（pathSum）等于target时和路径和大于target（并非所有路径和都等于target，题目已经说明每个元素都大于0），路径和等于target时将path加入到结果数组result中。时间复杂度为： $O(N * 2^{N})$ ，空间复杂度为 $O(N)$ 。

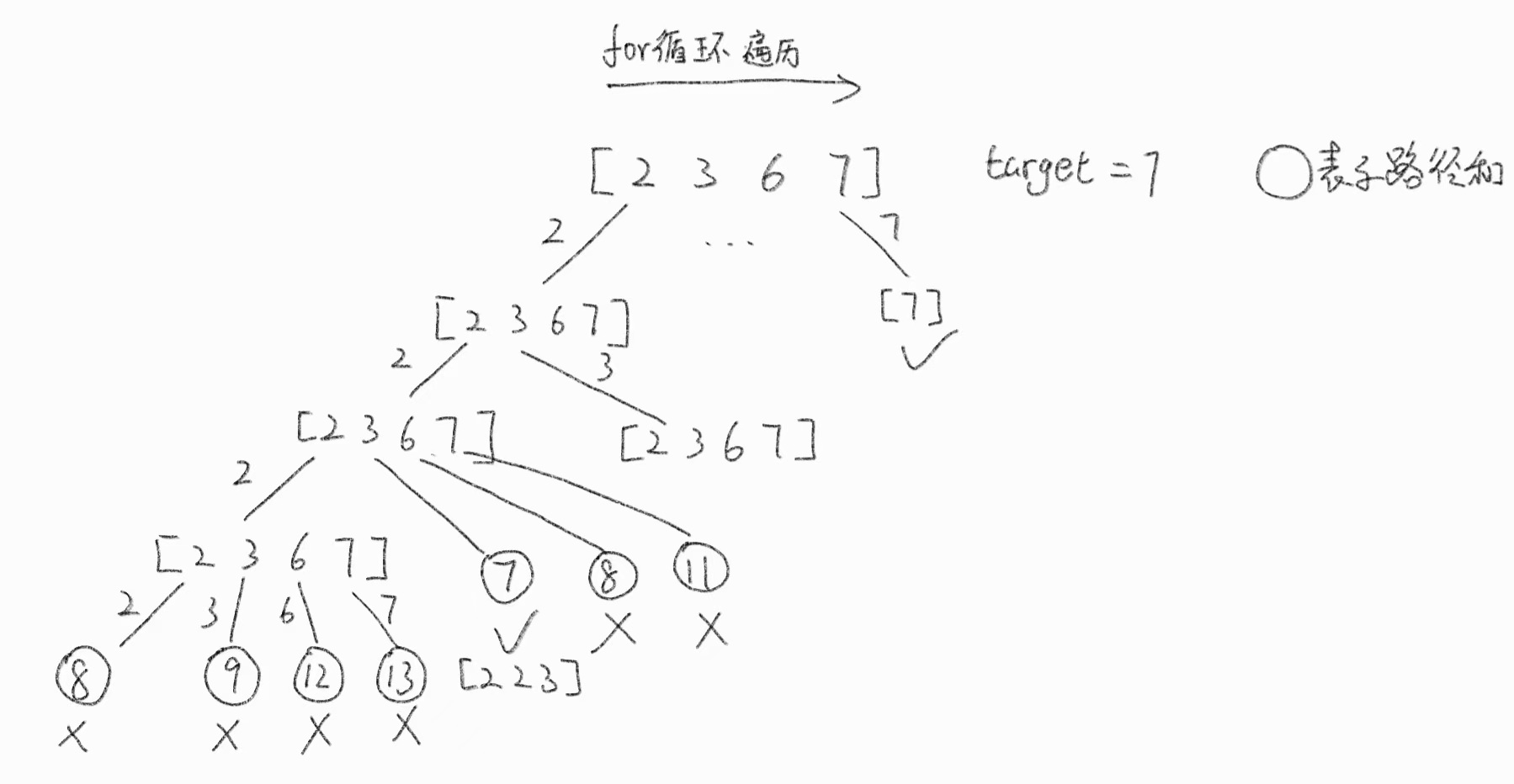
剪枝优化：先将candidates数组进行排序（先选择比target小得多的元素进行组合，大于或等于target的元素直接剪枝），再进行回溯，在for循环中再添加一个if判断：当pathSum + candidates[posIdx] > target时直接break退出循环，因为这个部分的组合已经不可能在组合成等于target的组合了。

代码：

回溯法：

class Solution {
public:vector<vector<int>> result;vector<int> path;int pathSum = 0;void backtracking(vector<int> &candidates, int posIdx, int target){if(pathSum == target){result.push_back(path);return;} else if(pathSum > target){return;}for(int idx = posIdx; idx < candidates.size(); idx++){path.push_back(candidates[idx]);pathSum += candidates[idx];backtracking(candidates, idx, target);int popVal = path.back();path.pop_back();pathSum -= popVal;}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {backtracking(candidates, 0, target);return result;}
};

剪枝优化：

class Solution {
public:vector<vector<int>> result;vector<int> path;int pathSum = 0;void backtracking(vector<int> &candidates, int posIdx, int target){if(pathSum == target){result.push_back(path);return;} else if(pathSum > target){return;}for(int idx = posIdx; idx < candidates.size(); idx++){if(pathSum + candidates[idx] > target) break;path.push_back(candidates[idx]);pathSum += candidates[idx];backtracking(candidates, idx, target);int popVal = path.back();path.pop_back();pathSum -= popVal;}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {sort(candidates.begin(), candidates.end());backtracking(candidates, 0, target);return result;}
};

LeetCode 40. 组合总和II

链接：40. 组合总和 II - 力扣（LeetCode）

思路：

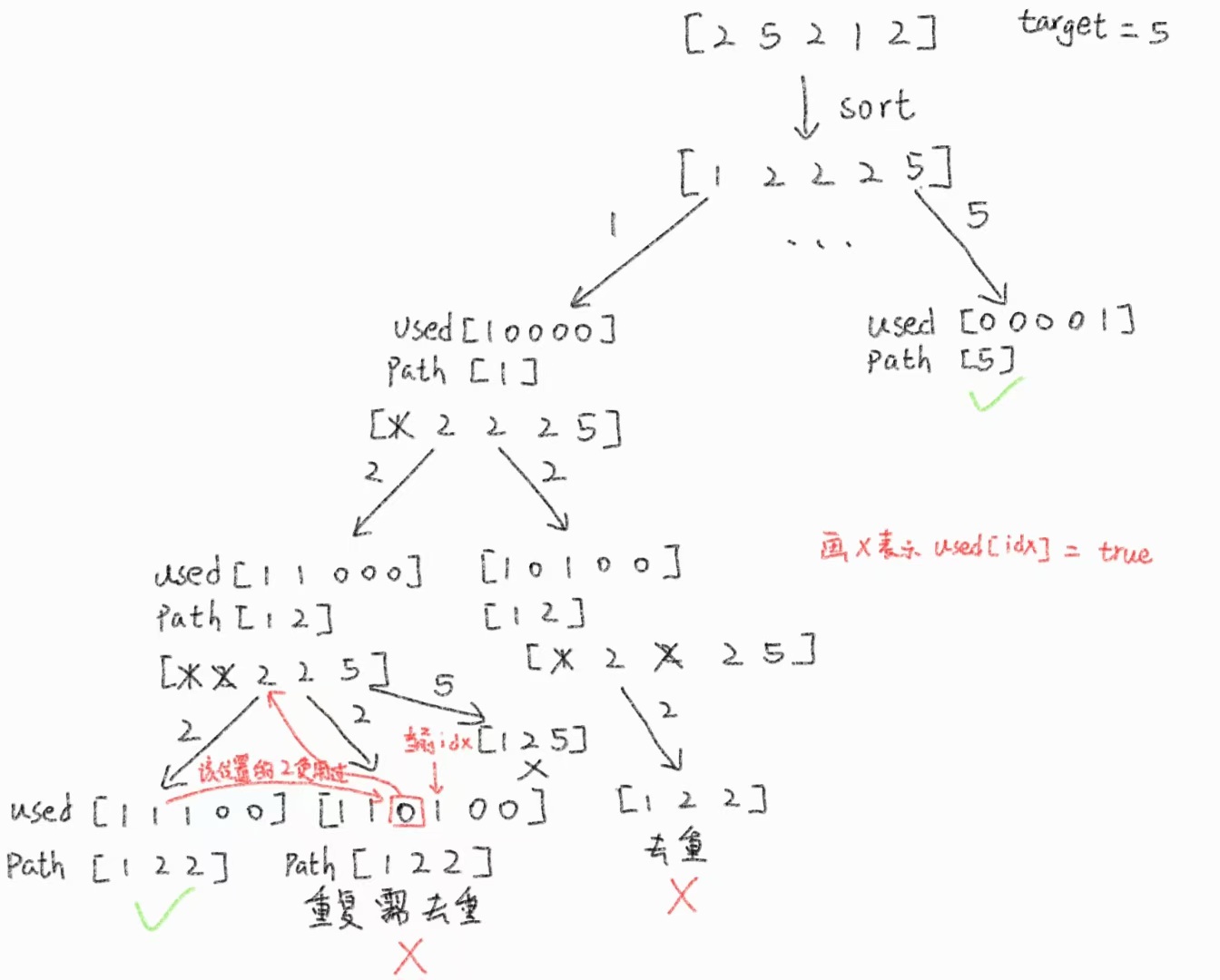
回溯法：思路和39题大致上相同，回溯终止的条件和39题一样，区别就是39题是允许元素的位置重复（即这个位置的元素使用过后还可用继续使用）的，本题的组合是不允许元素位置重复的，那么回溯中的for循环遍历就需要重新修改。因为元素位置不允许重复，所有可以设置一个数组来记录对应元素下标位置的使用情况，再往下层递归时，used数组是用于回溯for循环遍历中树的一层中需要跳过的下标（并不是向下递归需要跳过的下标，因为本题的回溯递归的开始位置每次都会加1，不会出现重复使用上一层使用过的位置），可以这样来理解：将初始传入数组排完序后，尽量在数组靠前部分找出所有的符合的组合，每个不同元素的第一个出现的元素开始组合，其后相同于第一个元素的元素再进行组合时必定会和第一个元素的组合结果重复，所以需要去重：candidates[idx] == candidates[i - 1] && used[idx - 1] = false 这一句表示的是在同一树层上的相同元素存在使用过的元素（使用过的元素再进行使用组合必定会重复）。时间复杂度为 $O(N * 2^{N})$ ，空间复杂度为 $O(N)$ 。

代码：

class Solution {
public:vector<int> path;vector<vector<int>> result;void backtracking(vector<int>& candidates, int target, int sum, int startIdx, vector<bool>used){if(sum == target){result.push_back(path);return;} else if(sum > target){return;}for(int idx = startIdx; idx < candidates.size(); idx++){if(idx > 0 && candidates[idx - 1] == candidates [idx] && used[idx - 1] == false){continue;}path.push_back(candidates[idx]);sum += candidates[idx];used[idx] = true;backtracking(candidates, target, sum, idx + 1, used);path.pop_back();sum -= candidates[idx];used[idx] = false;}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(), candidates.end());vector<bool>used(candidates.size(), false);int sum = 0;backtracking(candidates, target, sum, 0, used);return result;}
};

LeetCode 131. 分割回文串

链接：131. 分割回文串 - 力扣（LeetCode）

思路：

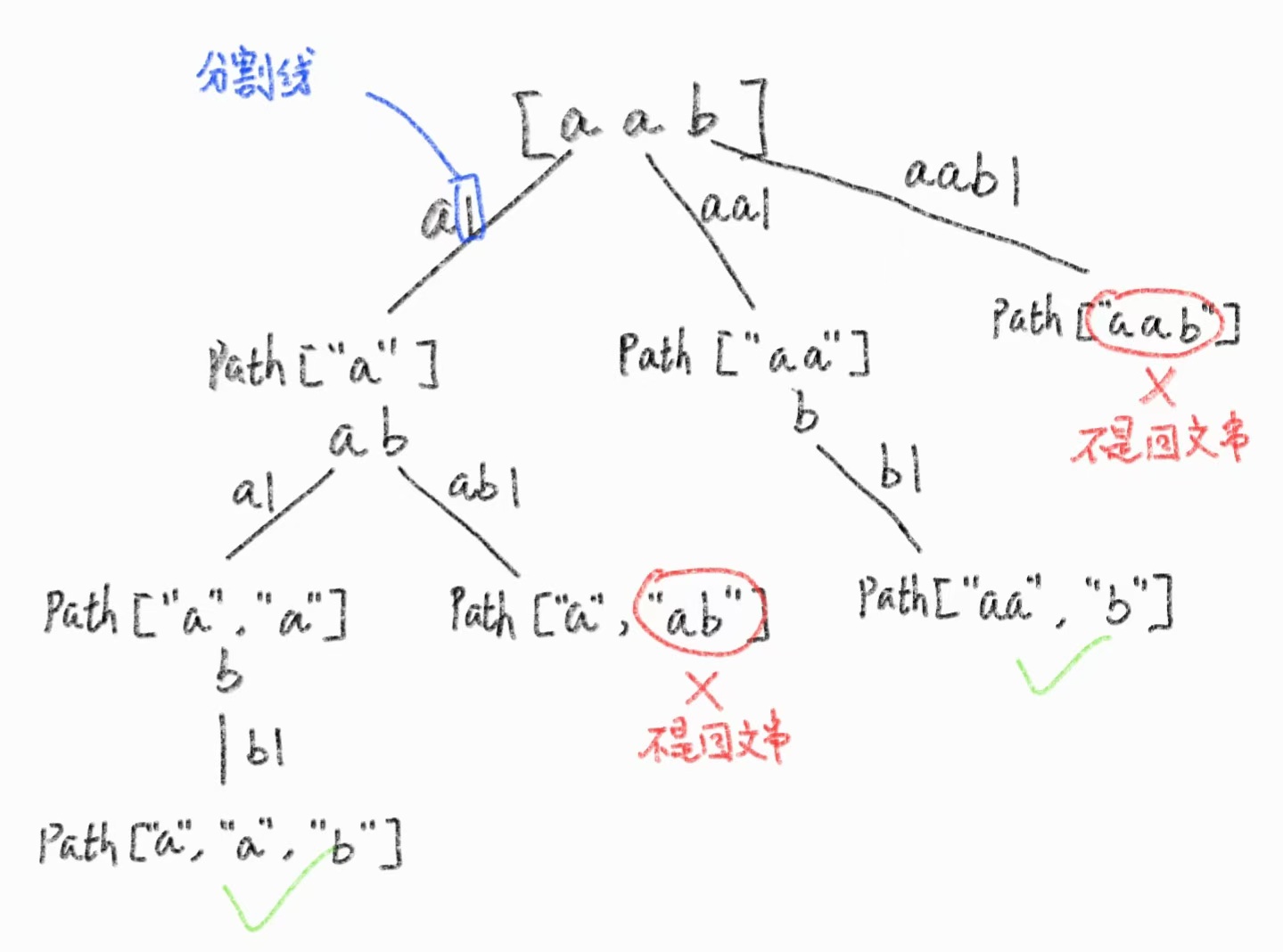
回溯法：这题使用回溯法和以往几题有所不同，本题是选取分割线的位置进行分割子串，并判断该子串是否是回文串（从前往后和从后往前的元素全部一致），将符合条件的这些子串加入到结果数组中。关键就是如何划分分割线形成一个子串：请参考下图。很明显下标区间就是对应分割线划分的子串，比如：下标0划分的子串就是a，下标0到1划分的子串就是aa，下标0到2划分的子串就是aab。因此代码就不难写了，在回溯for循环中先判断本次传入子串是否满足回文，若满足，则将该子串加入到路径path中继续递归，若不满足则继续开始下一个位置划分；当当前path的长度已经等于candidates主串的长度说明形成一组满足要求划分的子串，将其加入到结果数组中，继续递归直至找出所有满足的子串。时间复杂度为 $O(N * 2^{N})$ ，空间复杂度为 $O(N^{2})$ 。

代码：

回溯法：

class Solution {
public:vector<vector<string>> result;vector<string> path;bool isPalindrome(string &s, int begin, int end){while(begin < end){if(s[begin] != s[end]) return false;begin++;end--;}return true;}void backtracking(string &s, int startIdx){if(startIdx == s.size()){result.push_back(path);return;}for(int idx = startIdx; idx < s.size(); idx++){if(isPalindrome(s, startIdx, idx)){path.push_back(s.substr(startIdx, idx - startIdx + 1));backtracking(s, idx + 1);path.pop_back();} else {continue;}}}vector<vector<string>> partition(string s) {backtracking(s, 0);return result;}
};

查看全文

http://www.lryc.cn/news/613558.html