力扣137:只出现一次的数字Ⅱ

题目

给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。

思路

这道题目第一眼就能想到哈希表，所以可以直接秒了？不，看题目的要求时间复杂度要O(n)空间复杂度要O(1)。如果使用哈希表那么空间复杂度就不符合题目了。
所以我们需要换一个思路，一个整型有32个bit位每个bit位不是1就是0所以如果这个数字出现了三次并且将每一位的值相加，那么最后这32位不是0就是3所以我们可以把这32位依次取模3，出现三次的数字就直接归零了只有出现一次的数字才可以幸免遇难。但是这种方法需要在外层再遍历第0~31个二进制位，所以时间复杂度就变成了O(nlogC)其中n是数组的长度，C是数据的范围也就是整数的二进制位数。
虽然这个方法没法用了但是这个思想我们可以保留，我们没法对32位进行循环但是32位每一位都是一样的那么我们使用一位来进行判断不也可以吗。当我们对3进行取模后最后的值只有0，1，2所以我们把这三个值当作三个状态，并且这三个状态之间是可以进行变化的。变化过程我们可以用一张图来说明

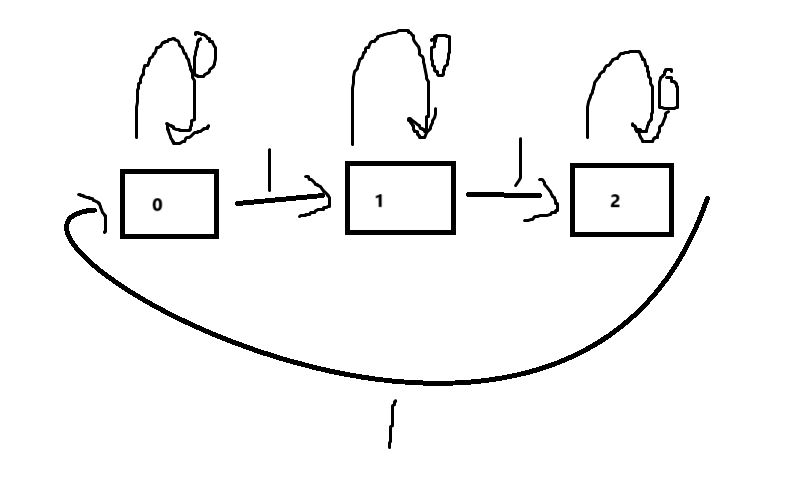
我们来解释一下这张图，对于一个二进制来说只有0和1两个值所以在输入二进制位1后就会进行状态变化，变化的过程就是：0->1->2->0->…，在输入二进制位0后就不会变化。
不好理解的话大家可以想一下上面说的对数组中每个元素的32二进制位进行相加，出现三次的元素的二进制位不就是从0变成1变成2变成3。但是我们最后又要对3进行取模所以3就是0那么最后的二进制位变化过程不就是从0变成1变成2再变成0吗。这就是三种状态的转换。
既然是对二进制位进行状态的模拟那么肯定不能出现2所以我们使用两位二进制来代表三个状态如下图。

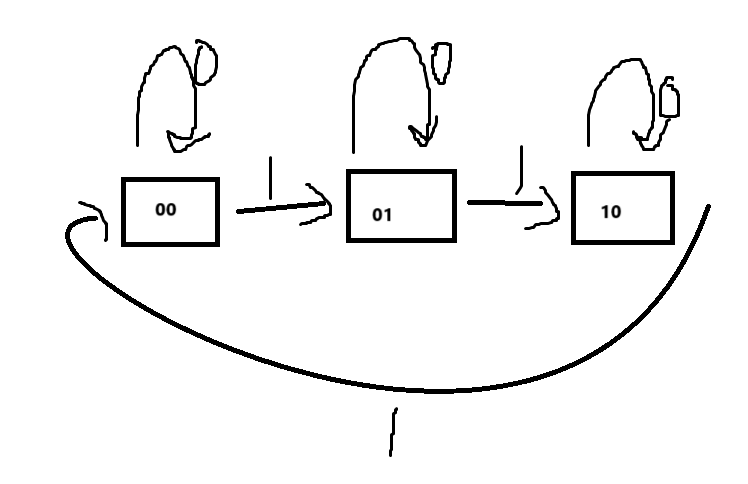
在变成了两位二进制位来表达状态后我们就需要来计算这两位的值分别都是怎么变化的了，也就是他们的状态变化方程。我们把这两位分别叫做two和one，每次输入的值叫做n

• 对于one来说：
  我们首先要对two的值进行判断，当two等于1时无论n是0还是1最后one都是0，当two等于0时我们就需要再对n进行判断，如果n是1那么one = ~one，如果n是0那么one=one。我们可以用一点伪代码来表示

if two == 0if n == 0one = oneif n == 1one = ~one
if two == 1one = 0//n为0，one就是本身。n为1，one就要取反。
//这不就是将one和n进行异或计算吗，所以可以简化
if two == 0one = one ^ n
if two == 1one = 0//two为1，one就为0。two为0，one就可以有值
//这不是很与运算很像吗，所以还可以简化
one = one ^ n & ~two

所以one的计算方式最终就是为one = one ^ n & two。

• 对于two来说：
  那么two要如何运算呢？相同的，我们可以把two和one进行交换也可以反过来看two就是反过来的one，one就是反过来的two。所以two的计算方式就是two = two ^ n & ~one。

在了解了这两个位置的计算方式我们就可以直接遍历数组了，那么最后的返回值是什么呢？数组中一共只有两种数字，出现一次的和出现三次的。出现一次的只会有一次输入的二进制位为1所以状态就是01，而出现三次的元素一共有三次输入二进制位为1所以最后的状态也就是00。所以我们最后只需要返回one就可以了。
注意我们模拟的只是一个二进制位的状态转变过程，但是一个整数有32个二进制位所以最后one的值就是元素本身的值！！！
这种办法我们的时间复杂度为O(n)，空间复杂度为O(1)。

代码

class Solution {
public:int singleNumber(vector<int>& nums) {int two = 0,one = 0;//题目说了只有一个数出现了一次，其他的数都是三次！！！for(auto ch : nums){one = one^ch & ~two;two = two^ch & ~one;}return one;}
};