当前位置：首页 > news >正文

解析图像几何变换：从欧式到仿射再到透视

news 2025/8/6 9:21:06

什么是图像几何变换？

图像几何变换，简单来说，就是通过一系列数学运算，对图像的空间位置进行“重新安排”。它不涉及颜色或像素值的改变，而是改变像素在图像中的位置。我们可以把它理解为：把图像绘制到带有弹性的橡皮上，通过旋转、平移、拉伸、扭曲等方式，重新塑造这图像的形状和角度。

为什么我们需要几何变换？因为在实际应用中，图像往往不是理想状态：

在某些应用中，我们可能需要调整图像的拍摄角度。如我们在扫描二维码时，不管什么角度都可以正确识别，这是因为在进行二维码识别前进行了图像几何变换的校正；
当拍照的文档歪了、扭曲了，想要变成“正面”图，我们可以通过透视变换对其进行矫正；
在训练神经网络，通过对原始图像做进行一些几何变换来扩展数据集，从而提高模型的鲁棒性。

根据变换的复杂程度和变换后保留的几何特性，几何变换大致可以分为以下几类：

欧式变换（Euclidean transform）：只包括旋转和平移，保持距离和角度不变；
仿射变换（Affine transform）：在线性基础上增加缩放、剪切等操作，保持直线和比例；
透视变换（Perspective transform）：模拟真实世界中的远近变化，可以进行更复杂的三维感变形。

欧式变换：保持形状的基础变换

欧式变换（Euclidean Transform），也称为刚体变换（rigid transform），是最基础的一种图像几何变换。它包括旋转（rotation）与平移（translation）两种操作，不涉及缩放、拉伸或形变。我认为称为刚体变换更加容易理解：我们可以想象对于一个坚硬的物体来说，我们唯二能做的事情就是将其平移到某个位置或者对其进行角度旋转。很显然，在变换过程中保持图像中物体的距离、角度、形状与面积不变。

接下来我们使用数学表达式描述二维空间的欧式变换，使用 $\begin{bmatrix} x\\ y \end{bmatrix}$ 表示变化前坐标，使用 $\begin{bmatrix} x^{'}\\y^{'} \end{bmatrix}$ 表示变换后的坐标。

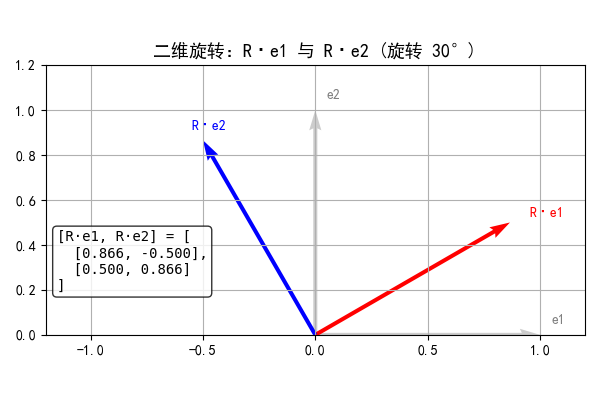
对物体平移 $\begin{bmatrix} t_{x}\\ t_{y} \end{bmatrix}$ ，我们可以自然的表达为： $\begin{bmatrix} x^{'}\\y^{'} \end{bmatrix}=\begin{bmatrix} x\\y \end{bmatrix}+\begin{bmatrix} t_{x}\\t_{y} \end{bmatrix}$ 。

对物体旋转某一角度 $\theta$ ，我们使用变换 $T$ 表示。对于向量 $\begin{bmatrix} x\\ y \end{bmatrix}$ ，我们可以将其拆分为 $x$ 与 $y$ 轴上基向量的和： $\begin{bmatrix} x\\ y \end{bmatrix}=x\begin{bmatrix} 1\\ 0 \end{bmatrix}+y\begin{bmatrix} 0\\ 1 \end{bmatrix}$ 。这样的拆分看起来有些冗余，实际上会很有益处。

接下来对向量 $\begin{bmatrix} x\\ y \end{bmatrix}$ 施加旋转变换 $T$ 可表示为： $T\begin{bmatrix} x\\ y \end{bmatrix}=x(T\begin{bmatrix} 1\\ 0 \end{bmatrix})+y(T\begin{bmatrix} 0\\ 1 \end{bmatrix})$ ，该表达是线性运算的基本性质，我们这里不予以证明。该表达式可理解为：对于任意向量 $\begin{bmatrix} x\\ y \end{bmatrix}$ 施加旋转变换 $T$ ，等价于分别对其基向量（如 $\begin{bmatrix} 1\\ 0 \end{bmatrix},\begin{bmatrix} 0\\ 1 \end{bmatrix}$ ）施加变换 $T$ ，然后再进行线性组合。因此，我们这里将问题转换为计算 $T\begin{bmatrix} 1\\ 0 \end{bmatrix}$ 和 $T\begin{bmatrix} 0\\ 1 \end{bmatrix}$ 的结果。根据三角函数相关知识，对 $\begin{bmatrix} 1\\ 0 \end{bmatrix}$ 绕原点逆时针旋转 $\theta$ 得到坐标为 $\begin{bmatrix} cos\theta\\ sin\theta \end{bmatrix}$ ，对 $\begin{bmatrix} 0\\ 1 \end{bmatrix}$ 绕原点逆时针旋转 $\theta$ 得到坐标为 $\begin{bmatrix} -sin\theta\\ cos\theta \end{bmatrix}$ 。

有了基向量的变换结果，代入原公式可得： $T\begin{bmatrix} x\\y \end{bmatrix}=x\begin{bmatrix} cos\theta\\ sin\theta \end{bmatrix}+y\begin{bmatrix} -sin\theta\\ cos\theta \end{bmatrix}$ ，进一步整理矩阵得： $T\begin{bmatrix} x\\ y \end{bmatrix}=\begin{bmatrix} cos\theta &-sin\theta \\ sin\theta& cos\theta \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}$ 。

到此，我们得到： $\begin{bmatrix} x^{'}\\ y^{'} \end{bmatrix}=\begin{bmatrix} cos\theta & -sin\theta\\ sin\theta & cos\theta \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}$ ，实现了绕原点逆时针旋转 $\theta$ 的变换。这里需要注意的是：旋转定义是绕原点旋转，且为逆时针旋转，这是关于旋转定义的默认规则！

仿射变换：保持平行性

仿射变换（Affine Transformation）在欧式变换（旋转 + 平移）的基础上引入了缩放、剪等更加广泛的线性变换，仿射变换保持线段间的平行性不被改变，但不再具备欧式变换中保持角度的性质。更加准确的说，仿射变换是任意线性变换叠加一个平移操作，而欧式变换对线性变换部分做了限制，即欧式变换将线性变换部分限制在旋转矩阵这种特殊类型的线性变换中 (所有旋转矩阵构成了一个李群，多视图几何中相机位姿的估计就会利用李群概念)。

根据仿射变换的定义，我们可以将其写作 $\begin{bmatrix} x^{'}\\y^{'} \end{bmatrix}=\begin{bmatrix} a &b \\ c & d \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}+\begin{bmatrix} t_{x}\\ t_{y} \end{bmatrix}$ ，这里线性变换部分 $\begin{bmatrix} a & b\\ c & d \end{bmatrix}$ 不再是旋转矩阵，它可能是更加广泛的任意线性变换。但如果 $\begin{bmatrix} a & b\\ c & d \end{bmatrix}$ 的行列式为0(即不可逆)，我们认为这不是一个有效的仿射变换。因为不可逆矩阵的线性变换将二维平面上的点压缩为一条直线上的点，这样就丢失了图像中的信息。所以，我们考虑的仿射变换要求线性变换部分应该是可逆的。

对于欧式变换来说，旋转与平移不改变物体的形状，这个形状我们可以很直观的感受到。但对于仿射变换保持平行性的性质，我们需要一些推导才能够豁然开朗。

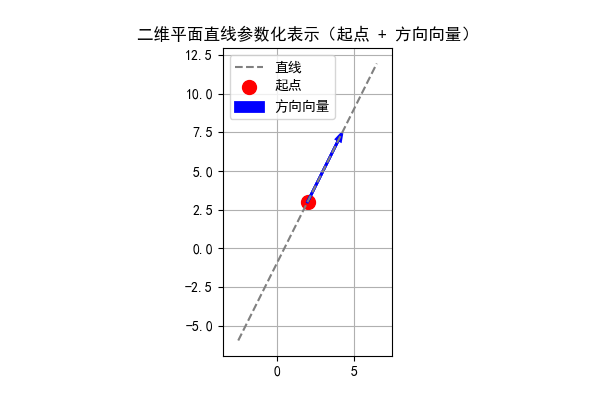
直线的定义可以这样表示：二维平面上有一个点 $p$ 表示直线的起点，在起点上有一个方向向量 $\vec{d}$ 表示该直线的方向，则直线上任意点的坐标可使用参数方程表示为： $l(t)=p+t\vec{k}$ ，其中 $k$ 为任意实数。

从直线的参数方程 $l(t)=p+t\vec{k}$ 表达来看，直线是 $p$ 与 $\vec{k}$ 的线性组合，对直线的仿射变换等价于对 $p$ 与 $\vec{k}$ 的仿射变换后的线性组合，即 $T(l(t))=T(p)+tT(\vec{k})$ ，整理得：

$(\begin{bmatrix} a & b\\ c &d \end{bmatrix}p+(1+t)\begin{bmatrix} t_{x}\\t_{y} \end{bmatrix})+t(\begin{bmatrix} a & b\\ c& d \end{bmatrix}\vec{k})$ ，

令 $p^{'}=(\begin{bmatrix} a & b\\ c &d \end{bmatrix}p+(1+t)\begin{bmatrix} t_{x}\\t_{y} \end{bmatrix})$ ， $\vec{k^{'}}=(\begin{bmatrix} a & b\\ c& d \end{bmatrix}\vec{k})$ ，

我们得到仿射变换后的直线参数方程： $l^{'}(t)=p^{'}+t{\vec{k^{'}}}$ 。

对于两条平行线，参数方程的定义起点不一致，但必须满足两条直线的方向一致(都为 $\vec{k}$ )，那么经过同一仿射变换后的直线方向都为 $\vec{k^{'}}$ 。因此，经过仿射变换后原本平行的直线仍旧保持平行。

透视变换：仅保持直线性

透视变换（Perspective Transformation）也称为射影变换（Projective Transformation），是一种强大而灵活的几何变换方式。它模拟的是现实中由于相机投影模型引起的图像失真，例如：建筑物的近大远小、道路的汇聚等。透视变换不仅可以处理平移、旋转、缩放和剪切等仿射变换，还能描述“视角改变”带来的变形。

二维空间中，透视变换使用一个 3×3 的非奇异矩阵 $H$ 来表示： $\begin{bmatrix} x^{'}\\y^{'} \\ w^{'} \end{bmatrix}=\begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix}\begin{bmatrix} x\\ y \\ 1 \end{bmatrix}$ ，正如上面所诉，该模型描述了相机投影过程，因此我们可以通过研究相机成像模型推导出3D空间到2D平面的透视投影矩阵，这是一个4*3的投影矩阵。那么，对于2D到2D的透视变换，则可类似使用3*3的矩阵表示。

变换前后的坐标均为齐次坐标，引入齐次坐标的目的是将非线性运算转换为线性运算。因此，要得到最终的图像坐标，需要进行齐次坐标到图像坐标的转换，具体如下：

$\left\{\begin{matrix} x^{'}=h_{11}x+h_{12}y+h_{13}\\ y^{'}=h_{21}x+h_{22}y+h_{23}\\ w^{'}=h_{31}x+h_{32}y+h_{33} \end{matrix}\right.$ ，为透视变换后得到的齐次坐标；

$\left\{\begin{matrix} x^{''}=\frac{x^{'}}{w^{'}} \\ y^{''}=\frac{y^{'}}{w^{'}} \end{matrix}\right.$ ，获得具体的欧式坐标。

我们发现对透视变换矩阵 $H$ 乘以任意一个系数，其变换后的欧式坐标都是一致的。因此，透视矩阵仅有8个自由度，我们可以通过不共线的对应点唯一确定一个透视矩阵。同时，由于透视矩阵的可逆性，使得透视变换具有一对一变换的特性，即存在一个逆变换对变换后数据进行恢复。

透视变换能够保持的几何性质不多，最主要的性质就是保持直线性。我们给出简单证明：

令直线表示为 $l^{T}\vec{x}=0$ ，其中： $l=\begin{bmatrix} a\\ b \\ c \end{bmatrix}$ 为直线方程的系数， $\vec{x}=\begin{bmatrix} x\\ y \\ 1 \end{bmatrix}$ 为直线上任意点的齐次坐标，很显然， $l^{T}\vec{x}=\begin{bmatrix} a& b & c \end{bmatrix}\begin{bmatrix} x\\ y \\ 1 \end{bmatrix}=ax+by+c=0$ ；

对直线上任意点 $\vec{x}$ 进行透视变换得到 $\vec{x^{'}}=H\vec{x}$ ，代入直线方程有： $l^{T}(H^{-1}\vec{x^{'}})=0$ ，

整理得： $(H^{-T}l)^{T}\vec{x^{'}}=0$ ，因此任意变换后点 $\vec{x^{'}}$ 仍旧位于一条直线上。

OpenCV提供的接口解析

OpenCV对图像几何变换提供了一系列函数，主要包括两类：

仿射变换接口
透视变换接口

为什么没有提供欧式变换接口呢？其实仿射变换与欧式变换的变换矩阵基本一致，都为 $\begin{bmatrix} a &b&t_{x} \\ c&d &t_{y}\\ 0 & 0&1 \end{bmatrix}$ ，欧式变换仅在线性变换部分存在一些约束。因此，OpenCV将欧式变换作为仿射变换的子集包含在一个接口中。

cv::warpAffine

函数cv::warpAffine提供了仿射变换与欧式变换的具体变换实现。通过传入变换矩阵 $M$ 以执行不同类型的仿射变换，因此变换矩阵 $M$ 的生成至关重要。有两个函数可以生成适合cv::warpAffine的变换矩阵，包括：

cv::getRotationMatrix2D(Point2f center, double angle, double scale)
cv::getAffineTransform(InputArray src, InputArray dst)

cv::getRotationMatrix2D获得一个旋转变换矩阵，定义为绕中心点center逆时针旋转anlge角度。因此，我们需要传入旋转中心点以及旋转角度。注意，这里的旋转角度需要传入角度值而非弧度值。另外，scale参数引入了尺度变化（此类旋转变换上放大或者缩小图像被称作相似变换），如scale为1时表示尺度不变，大于1则放大图像，小于1则缩小图像。

我们注意到cv::getRotationMatrix2D获得的矩阵表示绕某个中心旋转某个角度，它并没有添加平移信息。如果我们的需求是绕某个中心旋转某个角度后再平移一定数量，我们应该如何实现呢？我们可以首先通过cv::getRotationMatrix2D获得旋转矩阵 $R$ ，然后再构造一个平移矩阵 $T=\begin{bmatrix} 1 & 0 &t_{x} \\ 0 & 1& t_{y}\\ 0 & 0& 1 \end{bmatrix}$ ，最终的变换可以通过矩阵乘法表示 $M=TR$ 。我们将 $M$ 作为参数传给cv::warpAffine即可实现旋转加平移操作。

cv::getAffineTransform获得一个仿射变换矩阵，仿射变换矩阵难以像旋转变换矩阵那样直观描述，如旋转多少度等语言。我们可以通过三个不共线的对应顶点对来求解仿射变换矩阵，也就是说：三个不共线的对应顶点对唯一确定一个仿射变换。想象一下，对于一个矩形施加仿射变换后，矩形的四个顶点的坐标显然会发生变化，通过记录变化前后的点对坐标，即可求解一个唯一的仿射变换。那么，对于一个矩形来说，我们只需要知道三个顶点的坐标即可构造仿射变换，理由是仿射变换保持平行性，矩形的平行性使得我们通过变换后的三个点即可恢复变换后的平行四边形。

cv::getAffineTransform的src参数输入变换前的三个不共线点坐标，dst参数表示变换前三个不共线点经过仿射变换后的坐标（一般情况下，变换后的坐标也不会共线）。cv::getAffineTransform函数根据src与dst即可计算出仿射变换矩阵。

到目前为止，我们基本理清了仿射变换相关的核心接口函数。另外有两个补充函数可以为我们的应用提供便利。

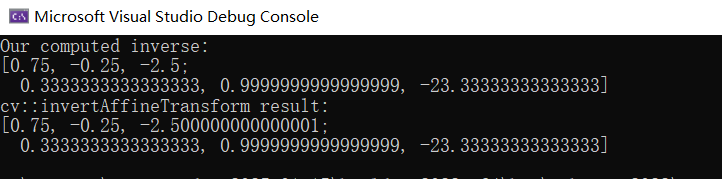
cv::invertAffineTransform提供了仿射变换的逆变换接口。由于仿射变换是一对一的，我们可以通过该函数求解仿射变换的逆变换。其实，如果我们将2*3的仿射变换拓展到3*3维度，如： $\begin{bmatrix} a & b& t_{x}\\ c& c & t_{y} \end{bmatrix}$ ---> $\begin{bmatrix} a & b& t_{x}\\ c& c & t_{y}\\ 0& 0 & 1 \end{bmatrix}$ ，该函数等价于求解3*3矩阵的逆矩阵，然后取前两行构成2*3的仿射变换矩阵。以下代码证明两者等价：

void compare_directInvertMatrix_invertAffineTransform()
{// 构造一个仿射变换矩阵cv::Mat M = (cv::Mat_<double>(2, 3) << 1.2, 0.3, 10, -0.4, 0.9, 20);// 扩展为 3x3cv::Mat M33 = cv::Mat::eye(3, 3, CV_64F);M.copyTo(M33(cv::Rect(0, 0, 3, 2)));// 求逆cv::Mat M33_inv = M33.inv();// 提取前两行cv::Mat M_inv = M33_inv(cv::Rect(0, 0, 3, 2));// OpenCV 的结果cv::Mat M_cv_inv;cv::invertAffineTransform(M, M_cv_inv);// 对比std::cout << "Our computed inverse:\n" << M_inv << std::endl;std::cout << "cv::invertAffineTransform result:\n" << M_cv_inv << std::endl;
}

在某些情形下，我们可能不会对图像上所有点进行仿射变换。也就是说，我们可能仅需要对一些稀疏的离散点进行仿射变换，如对特征提取产生的点进行仿射变换。cv::transform接口就提供了我们所期望的功能，对于变换点的矩阵参数cv::InputArray src，cv::InputArray dst，每一行代表一个点。例如，我们需要对100个二维点进行仿射变换，src的维度为100*1(100行1列)，每一个元素下为两通道的数据点构成。dst亦为如此结构。

cv::warpPerspective

有了cv::warpAffine仿射变换的知识，我们就很容易理解透视变换的接口函数了。同样的，我们首先需要生成透视变换矩阵。对于透视变换矩阵，我们没有办法像欧式变换一样直观描述。在透视变换的理论讲解中，我们知道二维平面的透视变换有8个自由度，因此，我们可以传入4个不共线的点来计算出对应的透视变换。cv::getPerspectiveTransform函数提供了透视变换矩阵生成的功能，我们会在代码中给出使用示例。

和仿射变换类似，我们也有需要对一些稀疏点进行透视变换，cv::perspectiveTransform函数为我们提供了该功能的实现。

使用OpenCV进行图像几何变换

绕图像中心旋转45度

void roateByImageCenter()
{cv::Mat src = cv::imread("1_src.bmp", cv::IMREAD_COLOR);if (src.empty()) return;  // 检查是否成功读取图像// 绕图像中心旋转45度，执行如下步骤：// 1 将图像中心center平移到原点(-cx,-cy)// 2 施加旋转// 3 平移回原坐标(+cx,+cy)// 以上构成了绕中心旋转矩阵cv::Point2f center(src.cols / 2.0f, src.rows / 2.0f);// 参数scale表示缩放系数，大于1时放大图像，小于1时缩小图像// 这里使用scale=1保持图像尺寸（即仅欧式变换）cv::Mat M = cv::getRotationMatrix2D(center, 45, 1.);std::cout << "rotate 45 around image center:\n" << M << std::endl;cv::Mat dst;// 使用旋转矩阵M进行仿射变换// 参数flags表示几何变换时的插值仿射，我们使用默认双线性插值。如果期望更好效果，可根据实际需求修改。cv::warpAffine(src, dst, M, src.size());cv::imwrite("2_affine1.bmp", dst);// 通过变换后图像2_affine1.bmp，发现旋转后图像有截取，我们需要改变目标图像尺寸以容纳旋转后图像// 图像最宽处为对角线位置，当旋转到某个角度后对角线就变成了图像的宽或者高，因此变换后最大图像宽高为对角线！int diagonal = sqrt((double)(src.cols * src.cols + src.rows * src.rows));diagonal = (diagonal + 3) / 4 * 4;cv::warpAffine(src, dst, M, cv::Size(diagonal, diagonal));cv::imwrite("3_affine2.bmp", dst);// 通过变换后图像2_affine2.bmp，发现右下角的图像无截取，左上角仍旧存在截取！// (w,0)旋转acot(w/对角线)后在y轴上形成最小负数，(0,0)旋转acot(h/对角线)后在x轴上形成最小负数// y溢出：对角线*0.5-h*0.5，x溢出：对角线*0.5-w*0.5// 因此，旋转产生了负数坐标，而图像坐标都为正数，我们需要通过平移避免负数坐标！int offset_x = (diagonal - src.rows + 1) / 2;int offset_y = (diagonal - src.cols + 1) / 2;M.at<double>(0, 2) += offset_x;  M.at<double>(1, 2) += offset_y;  cv::warpAffine(src, dst, M, cv::Size(diagonal, diagonal));cv::imwrite("4_affine3.bmp", dst);// 到目前为止，变换后图像2_affine3.bmp基本达到了我们的预期效果:// 实现了绕图像中心旋转45度，同时确保旋转后图像没有有效数据的丢失！}

以上代码实现了绕图像中心点旋转45度的效果，代码通过启发式的思考引导我们一步一步实现我们的目标。首先，我们需要构造一个绕图像中心的旋转矩阵，然后我们需要调整变换后图像尺寸以避免数据溢出，最后我们发现需要处理旋转后负坐标问题才能够达到完美的预期效果。

关于构造绕图像中心的旋转矩阵，OpenCV给出了一个接口cv::getRotationMatrix2D，通过传入旋转中心以及旋转角度即可获得旋转矩阵。这里我们想更进一步理解它到底如何实现：它包含了三个关键操作。

将图像中心center平移到原点(-cx,-cy)
在新坐标下对图像旋转45度
反向平移(+cx,+cy)，以抵消平移产生的影响

以上每一个操作都可以表示为3*3的齐次矩阵，依次将他们进行乘法运算就得到了最终的结果（绕图像中心旋转45度），最后我们取前两行即为期望的矩阵。

下面为代码产生的图像序列：

任意仿射变换与透视变换

void affineAndPerspective()
{cv::Mat src = cv::imread("1_src.bmp", cv::IMREAD_COLOR);if (src.empty()) return;  // 检查是否成功读取图像// 使用getAffineTransform获取仿射变换矩阵// 需要3对点确定变换矩阵！cv::Point2f srcTri[] = {cv::Point2f(0, 0),cv::Point2f(src.cols - 1, 0),cv::Point2f(0, src.rows - 1)};cv::Point2f dstTri[] = {cv::Point2f(src.cols * 0.f, src.rows * .3f),cv::Point2f(src.cols * .9f, src.rows * .2f),cv::Point2f(src.cols * .15f, src.rows * .8f)};cv::Mat M = cv::getAffineTransform(srcTri, dstTri);cv::Mat dst;cv::warpAffine(src, dst, M, src.size(), cv::INTER_CUBIC);cv::imwrite("2_affine.bmp", dst);// 使用getPerspectiveTransform获取透视变换矩阵// 需要4对点确定变换矩阵！cv::Point2f srcTri2[] = {cv::Point2f(0, 0),cv::Point2f(src.cols - 1, 0),cv::Point2f(0, src.rows - 1),cv::Point2f(src.cols - 1, src.rows - 1)};cv::Point2f dstTri2[] = {cv::Point2f(src.cols * 0.f, src.rows * .3f),cv::Point2f(src.cols * .9f, src.rows * .2f),cv::Point2f(src.cols * .15f, src.rows * .8f),cv::Point2f(src.cols * .7f, src.rows * .7f)};cv::Mat M2 = cv::getPerspectiveTransform(srcTri2, dstTri2);cv::Mat dst2;cv::warpPerspective(src, dst2, M2, src.size(), cv::INTER_CUBIC);cv::imwrite("3_perspective.bmp", dst2);
}

以上代码实现了任意仿射变换与任意透视变换。首先我们需要根据一些数据获取变换矩阵，然后再基于变换矩阵对所有数据施加通过一个变换。在实际应用中，获取变换矩阵是一个关键步骤。我们可能有以下方式获取变换矩阵：

通过手动标记不同图像上的对应点对获得变换矩阵
通过特征点提取的方式获取匹配点对，从而获取对应的变换矩阵

以下是仿射变换与透视变换的效果图像：

总结

本文首先讲解了图像几何变换的基本性质，包括：欧式变换（旋转和平移）、仿射变换（增加缩放和剪切）、透视变换（模拟三维远近效果）。然后对OpenCV提供cv::warpAffine和cv::warpPerspective等接口进行了深度剖析。在函数剖析中，我们并没有机械的说明每个参数的含义，而是着重讲解一些重点参数的使用。最后，通过代码示例展示了图像几何变换的基本应用，使得大家可以在项目中真正使用相关功能。

查看全文

http://www.lryc.cn/news/610837.html