向量魔法：Embedding如何赋能大模型理解世界

一、引言

在人工智能的浪潮中，大模型（Large Models）以其卓越的性能和广泛的应用场景，成为了科技领域最受关注的焦点之一。从自然语言处理（NLP）到计算机视觉（CV），再到推荐系统，大模型正在以前所未有的方式改变着我们与世界的互动。然而，这些看似“智能”的模型背后，离不开一个核心且基础的技术支撑——Embedding（嵌入）。

Embedding，作为一种将高维、离散的数据（如文字、图像、声音等）映射到低维连续向量空间的技术，极大地提升了计算机理解和处理复杂数据的能力。它不仅解决了传统机器学习方法在处理海量非结构化数据时面临的“维度灾难”问题，更重要的是，它赋予了数据以“语义”和“上下文”信息，使得计算机能够像人类一样，理解数据之间的深层联系和相似性。

本文将深入探讨大模型中Embedding的奥秘，从其基本定义、核心原理，到不同类型及其在各大领域的广泛应用，并通过图表、示例、伪代码和公式，力求为读者揭示Embedding如何成为大模型智能的基石。

二、什么是Embedding？

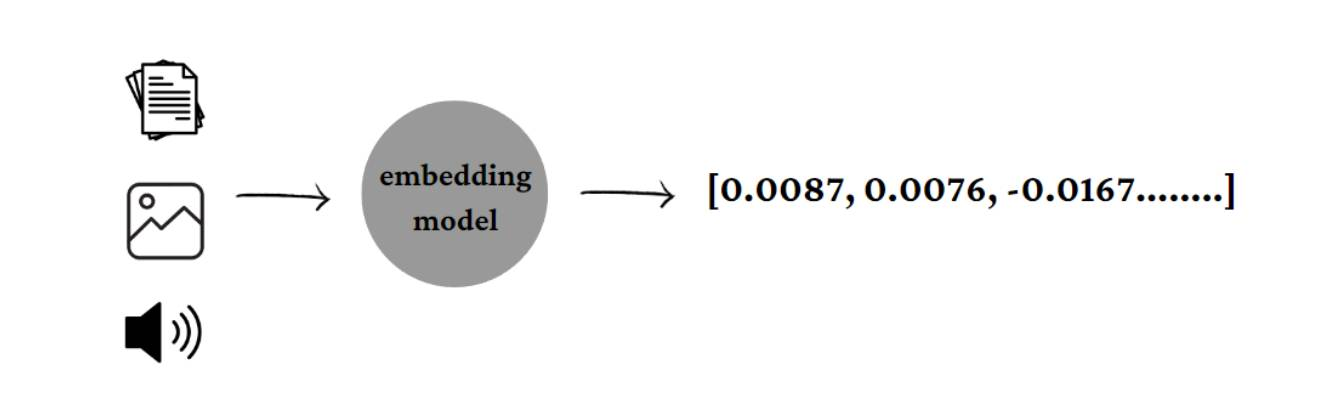
简单来说，Embedding是一种将现实世界中复杂、高维的数据（例如单词、句子、图像、用户ID、商品ID等）转换成低维、连续的数值向量的技术。这些向量通常被称为“嵌入向量”或“稠密向量”。

2.1 定义与目的

• 定义：Embedding是将离散的、通常是高维度的数据（如独热编码的词汇）映射到一个低维连续向量空间的过程。在这个向量空间中，每个数据点都被表示为一个实数向量。

• 目的：

  • 捕捉语义和上下文关系：Embedding的核心思想是，在向量空间中，语义或功能上相似的数据点（例如，在自然语言处理中，意思相近的词语）会彼此靠近，即它们的向量距离会很小。这使得计算机能够“理解”数据之间的相似性和关联性。
  • 解决维度灾难：在处理文本数据时，如果使用独热编码（One-Hot Encoding）来表示词汇，词汇量越大，向量维度就越高，这会导致“维度灾难”问题，即数据稀疏、计算量大、模型难以泛化。Embedding通过将高维稀疏向量映射到低维稠密向量，有效缓解了这一问题。
  • 使计算机理解非结构化数据：文本、图像、音频等非结构化数据无法直接被计算机理解和处理。Embedding提供了一种将这些数据转化为计算机可理解的数值形式的方法，为后续的机器学习任务（如分类、聚类、推荐等）奠定基础。

2.2 为什么需要Embedding？

想象一下，如果你想让计算机理解“苹果”和“香蕉”都是水果，并且它们之间有某种相似性。如果仅仅用简单的ID（比如苹果=1，香蕉=2）来表示，计算机无法得知它们之间的任何关系。而通过Embedding，我们可以将“苹果”和“香蕉”映射到向量空间中相近的位置，而将“国王”映射到较远的位置，这样计算机就能通过向量之间的距离来判断它们的相似性。

此外，对于大规模数据集，例如一个包含百万词汇的词典，如果使用独热编码，每个词都需要一个百万维的向量，其中只有一个位置是1，其余都是0，这不仅浪费存储空间，也使得计算效率低下。Embedding则可以将这些词映射到几百维的稠密向量，大大提高了效率和表达能力。

三、Embedding的原理

Embedding的核心原理是**“相似的事物在向量空间中距离相近”**。这意味着，如果两个词语在语义上相似，或者两个图像在内容上相似，那么它们对应的Embedding向量在向量空间中的距离（例如欧氏距离或余弦相似度）就会很小。反之，不相似的事物则会相距较远。

3.1 核心思想：相似性度量

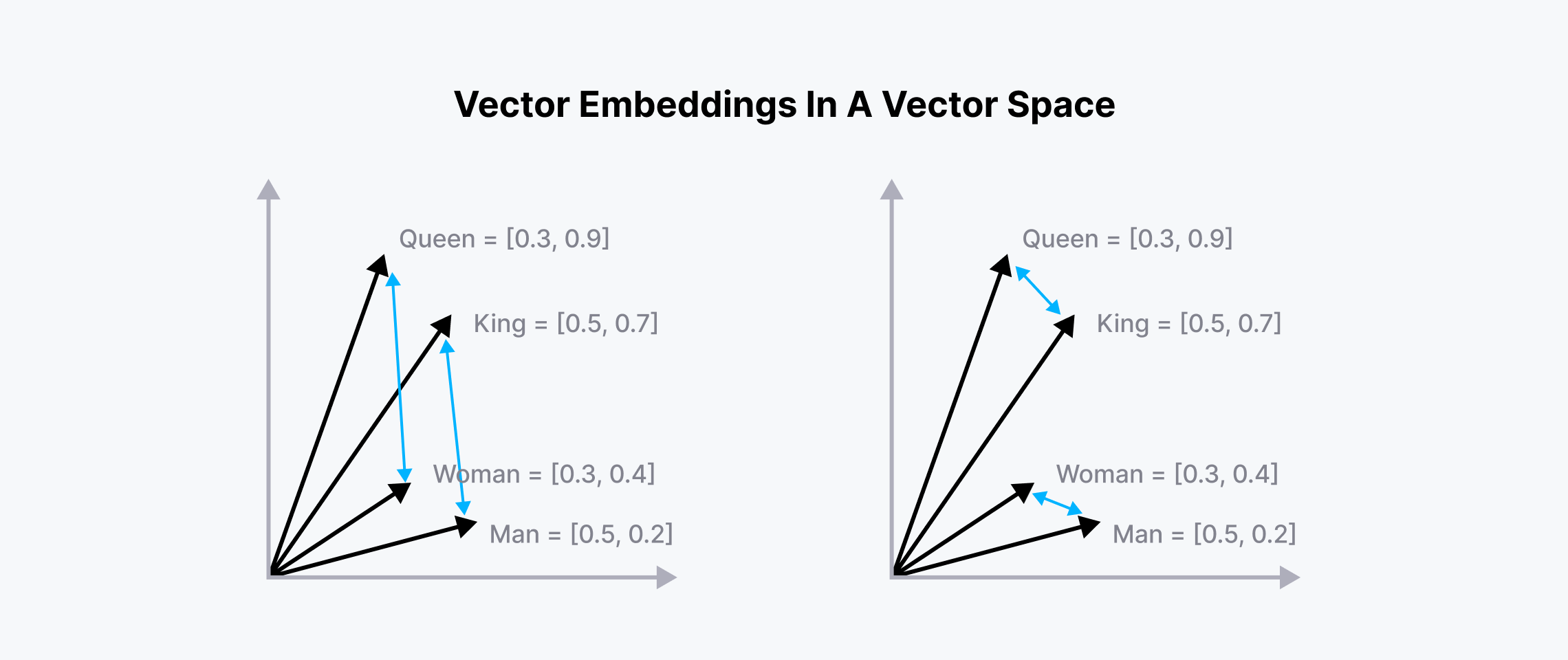
这种相似性度量是Embedding能够捕捉数据内在关系的关键。例如，在词嵌入中，“国王”和“女王”的Embedding向量会比“国王”和“汽车”的向量更接近。更进一步，词嵌入甚至能捕捉到复杂的语义关系，例如著名的“国王 - 男人 + 女人 = 女王”的类比关系，这在向量空间中表现为向量的加减运算。

3.2 如何学习Embedding：神经网络训练

Embedding向量通常不是人为设计的，而是通过机器学习模型（特别是神经网络）从大量数据中自动学习得到的。这个学习过程通常是无监督或半监督的，模型通过预测上下文、重构输入等任务来优化Embedding向量，使其能够更好地表示数据的内在特征。

以词嵌入为例，早期的Word2Vec模型通过两种架构来学习词向量：

• CBOW (Continuous Bag-of-Words)：根据上下文词语预测目标词语。
• Skip-gram：根据目标词语预测上下文词语。

无论哪种架构，其核心都是通过神经网络的训练，使得具有相似上下文的词语拥有相似的Embedding向量。在训练过程中，Embedding层（通常是一个查找表或一个全连接层）的权重会不断调整，直到模型能够很好地完成预测任务。

3.3 伪代码示例

以下是一个简化的伪代码示例，展示了如何通过神经网络学习词嵌入的基本概念：

# 假设我们有一个词汇表和对应的独热编码
vocabulary = {"我": 0, "爱": 1, "北京": 2, "天安门": 3, ...}# 假设Embedding维度为D
embedding_dim = 100# 初始化Embedding矩阵 (随机初始化)
# Embedding_Matrix 的形状是 (词汇表大小, embedding_dim)
Embedding_Matrix = initialize_random_matrix(len(vocabulary), embedding_dim)# 训练数据示例 (简化版：(上下文词, 目标词))
training_data = [("我", "爱"), ("爱", "北京"), ("北京", "天安门"), ...]# 训练过程 (简化)
for epoch in range(num_epochs):for context_word, target_word in training_data:# 获取上下文词的独热编码context_one_hot = one_hot_encode(context_word, vocabulary)# 通过Embedding层查找上下文词的Embedding向量# 实际上是矩阵乘法或查表操作context_embedding = dot_product(context_one_hot, Embedding_Matrix)# 使用神经网络预测目标词predicted_target_probabilities = neural_network(context_embedding)# 获取目标词的独热编码target_one_hot = one_hot_encode(target_word, vocabulary)# 计算损失 (例如交叉熵损失)loss = calculate_loss(predicted_target_probabilities, target_one_hot)# 反向传播和更新Embedding矩阵的权重Embedding_Matrix = update_weights_with_backpropagation(loss, Embedding_Matrix)# 训练完成后，Embedding_Matrix中的每一行就是一个词的Embedding向量
# 例如：embedding_of_我 = Embedding_Matrix[vocabulary["我"]]

在这个伪代码中，Embedding_Matrix就是我们最终学习到的Embedding。通过不断地调整这个矩阵的权重，模型使得语义相关的词语在向量空间中靠得更近。

四、常见的Embedding类型

随着人工智能技术的发展，Embedding的应用范围不断扩大，针对不同类型的数据和任务，也衍生出了多种Embedding类型。

4.1 Word Embedding (词嵌入)

词嵌入是最早也是最广泛应用的Embedding类型之一，它将文本中的每一个词语映射到一个低维向量。这些向量能够捕捉词语的语义和语法信息。

• Word2Vec：由Google在2013年提出，包括CBOW和Skip-gram两种模型，是词嵌入领域的里程碑式工作。它通过预测上下文或被上下文预测来学习词向量。
• GloVe (Global Vectors for Word Representation)：结合了全局矩阵分解和局部上下文窗口的方法，旨在捕捉词语的全局统计信息。
• FastText：由Facebook提出，与Word2Vec类似，但它将词语分解为字符级别的n-gram，因此能够处理未登录词（OOV）问题，并且在形态丰富的语言中表现更好。

4.2 Sentence Embedding (句嵌入)

句嵌入旨在将整个句子或段落映射到一个单一的向量，这个向量能够代表整个文本的语义信息。与词嵌入不同，句嵌入需要考虑词语之间的顺序和相互作用。

• 基于平均词向量：最简单的方法是将句子中所有词的词嵌入向量进行平均。然而，这种方法往往无法捕捉到词序和复杂的语义关系。
• 基于深度学习模型：BERT、ELMo、GPT等大型预训练语言模型（Large Language Models, LLMs）能够生成高质量的上下文相关Embedding。这些模型通过复杂的神经网络结构（如Transformer）学习词语在不同上下文中的表示，然后聚合得到句子的Embedding。例如，BERT的[CLS] token的输出向量常被用作句子的Embedding。

4.3 Image Embedding (图像嵌入)

图像嵌入是将图像数据转换为低维向量表示的技术。在向量空间中，内容相似的图像会具有相近的Embedding向量。

• 卷积神经网络 (CNN)：在图像识别任务中，通常使用预训练的CNN模型（如ResNet, VGG）的某个中间层的输出作为图像的Embedding。这些Embedding捕捉了图像的视觉特征。
• CLIP (Contrastive Language-Image Pre-training)：由OpenAI提出，它通过对比学习的方式，将图像和文本映射到同一个Embedding空间中。这使得模型能够理解图像和文本之间的语义关联，从而实现跨模态搜索和零样本学习。

4.4 Other Embeddings (其他类型)

Embedding的概念远不止于文本和图像，它可以应用于任何需要将离散实体转换为连续向量表示的场景，以便于机器学习模型处理。

• User Embedding (用户嵌入)：在推荐系统中，将用户的行为（如浏览、购买历史）映射为向量，以捕捉用户的兴趣和偏好。
• Item Embedding (物品嵌入)：将商品、电影、音乐等物品映射为向量，以捕捉物品的特征和属性。
• Graph Embedding (图嵌入)：将图结构数据（如社交网络、知识图谱）中的节点和边映射为向量，以保留图的结构信息和节点之间的关系。

这些不同类型的Embedding共同构成了大模型理解和处理多模态数据的基石，极大地扩展了AI的应用边界。

五、Embedding在大模型中的应用

Embedding技术是现代大模型能够实现各种复杂任务的基石。它将不同模态的数据统一表示为向量，使得模型能够高效地进行计算、比较和推理。以下是Embedding在大模型中的几个主要应用场景：

5.1 自然语言处理 (NLP)

在NLP领域，Embedding的应用无处不在，极大地提升了各种任务的性能：

• 语义搜索：通过将查询语句和文档内容都转换为Embedding向量，然后计算它们之间的相似度，可以实现比传统关键词匹配更智能的语义搜索，返回与查询意图更相关的结果。
• 问答系统：将问题和候选答案转换为Embedding，通过比较向量相似度来找到最佳答案。大模型如BERT、GPT等生成的上下文Embedding使得问答系统能够理解复杂的问题和语境。
• 文本分类：将文本（如新闻文章、用户评论）转换为Embedding向量，然后输入到分类器中，实现情感分析、垃圾邮件识别、主题分类等任务。
• 机器翻译：在神经机器翻译中，源语言的词语和句子被编码为Embedding，然后解码器利用这些Embedding生成目标语言的翻译。Embedding能够捕捉不同语言之间的语义对应关系。

5.2 推荐系统

推荐系统是Embedding的另一个重要应用领域。通过将用户和物品都表示为Embedding向量，可以高效地进行个性化推荐：

• 用户-物品匹配：将用户的历史行为（如购买、点击、浏览）和物品的特征（如类别、标签）分别转换为用户Embedding和物品Embedding。在向量空间中，用户Embedding与他们可能感兴趣的物品Embedding会非常接近。推荐系统通过计算用户Embedding与所有物品Embedding的相似度，来预测用户对未接触物品的偏好。
• 冷启动问题：对于新用户或新物品，由于缺乏历史数据，传统方法难以进行有效推荐。通过利用用户的注册信息或物品的元数据生成初始Embedding，可以缓解冷启动问题。

5.3 计算机视觉 (CV)

在计算机视觉领域，Embedding同样发挥着关键作用，尤其是在图像检索和识别方面：

• 图像检索：将图像转换为Embedding向量，构建图像数据库的向量索引。当用户上传一张图片进行搜索时，系统会计算查询图片的Embedding，然后在数据库中查找与其最相似的图像Embedding，从而实现“以图搜图”的功能。
• 图像识别：在图像分类、目标检测等任务中，图像的Embedding作为特征表示输入到后续的模型层，帮助模型识别图像中的内容。

5.4 跨模态学习

Embedding的强大之处还在于它能够实现不同模态数据之间的连接，即跨模态学习：

• 文本-图像关联：如CLIP模型所示，通过将文本和图像映射到同一个共享的Embedding空间，模型可以理解“猫”这个词语和猫的图片之间的关系。这使得可以实现文本描述生成图像、图像内容描述等任务。
• 多模态搜索：用户可以使用文本查询来搜索图像或视频，反之亦然。Embedding作为不同模态之间的桥梁，使得这种灵活的搜索成为可能。

六、Embedding的数学表示与计算

Embedding的本质是将离散的实体（如词语、图像）映射到连续的向量空间中。在这个空间里，我们可以利用数学工具来衡量实体之间的关系。

6.1 向量空间与距离度量

一个Embedding向量可以表示为一个n维实数向量：

$$\mathbf{v}=[v_1,v_2,\dots ,v_n]$$

其中，$n$ 是Embedding的维度。在向量空间中，衡量两个Embedding向量之间相似性的常用方法是计算它们之间的距离或相似度。

6.1.1 余弦相似度 (Cosine Similarity)

余弦相似度衡量的是两个向量在方向上的相似性，而不考虑它们的大小。它的值介于-1和1之间，1表示方向完全相同，-1表示方向完全相反，0表示相互正交（不相关）。

对于两个向量 $\mathbf{A}$ 和 $\mathbf{B}$，它们的余弦相似度定义为：

$$\text{cosine\_similarity}(\mathbf{A},\mathbf{B})=\frac{\mathbf{A}\cdot \mathbf{B}}{|\mathbf{A}|\cdot |\mathbf{B}|}=\frac{{\sum }_{i=1}^n{A}_i{B}_i}{\sqrt{{\sum }_{i=1}^n{A}_i^2}\sqrt{{\sum }_{i=1}^n{B}_i^2}}$$

其中，$\mathbf{A}\cdot \mathbf{B}$ 是向量的点积，$|\mathbf{A}|$ 和 $|\mathbf{B}|$ 分别是向量的欧几里得范数（或称L2范数）。

6.1.2 欧氏距离 (Euclidean Distance)

欧氏距离衡量的是两个向量在空间中的直线距离。距离越小，表示两个向量越接近。

对于两个向量 $\mathbf{A}$ 和 $\mathbf{B}$，它们的欧氏距离定义为：

$$\text{euclidean\_distance}(\mathbf{A},\mathbf{B})=\sqrt{\sum _{i=1}^n(A_i-B_i{)}^2}$$

6.2 举例说明

假设我们有三个词的2维Embedding向量：

• 猫：${\mathbf{v}}_{猫}=[0.8,0.6]$
• 狗：${\mathbf{v}}_{狗}=[0.7,0.7]$
• 汽车：${\mathbf{v}}_{汽车}=[-0.5,0.9]$

我们可以计算“猫”和“狗”之间的余弦相似度：

$$\text{cosine\_similarity}({\mathbf{v}}_{猫},{\mathbf{v}}_{狗})=\frac{(0.8)(0.7)+(0.6)(0.7)}{\sqrt{0.8^2+0.6^2}\sqrt{0.7^2+0.7^2}}=\frac{0.56+0.42}{\sqrt{0.64+0.36}\sqrt{0.49+0.49}}=\frac{0.98}{\sqrt{1}\sqrt{0.98}}=\frac{0.98}{1\cdot 0.9899}\approx 0.99$$

这个值非常接近1，表明“猫”和“狗”在语义上非常相似，这符合我们的直觉。

再计算“猫”和“汽车”之间的余弦相似度：

$$\text{cosine\_similarity}({\mathbf{v}}_{猫},{\mathbf{v}}_{汽车})=\frac{(0.8)(-0.5)+(0.6)(0.9)}{\sqrt{0.8^2+0.6^2}\sqrt{(-0.5{)}^2+0.9^2}}=\frac{-0.40+0.54}{\sqrt{1}\sqrt{0.25+0.81}}=\frac{0.14}{1\cdot \sqrt{1.06}}=\frac{0.14}{1.0295}\approx 0.136$$

这个值接近0，表明“猫”和“汽车”在语义上不相关，这也符合我们的直觉。

通过这些数学计算，Embedding成功地将抽象的语义关系转化为了可量化的数值关系，为机器学习模型提供了强大的特征表示。

七、总结与展望

Embedding技术是现代人工智能，特别是大模型领域不可或缺的基石。它通过将高维、离散的数据映射到低维、连续的向量空间，有效地解决了传统方法在处理非结构化数据时面临的挑战，并赋予了机器理解数据深层语义和上下文关系的能力。从最初的词嵌入到如今多模态、上下文相关的Embedding，这一技术的发展极大地推动了自然语言处理、计算机视觉、推荐系统以及跨模态学习等领域的进步。

随着数据模态的日益丰富和模型规模的不断扩大，如何学习到更高效、更具泛化能力、更能捕捉复杂关系的Embedding，将是未来的重要研究方向。例如，如何更好地融合不同模态的信息以生成统一的跨模态Embedding，如何处理长文本和复杂场景下的上下文依赖，以及如何提升Embedding的可解释性和鲁棒性，都将是值得探索的课题。可以预见，Embedding技术将继续在大模型的发展中扮演核心角色，驱动人工智能迈向新的高度。