当前位置：首页 > news >正文

06 基于sklearn的机械学习-欠拟合、过拟合、正则化、逻辑回归、k-means算法

news 2025/8/5 20:46:49

欠拟合、过拟合

欠拟合

过拟合

正则化

岭回归（Ridge Regression）：L2 正则化

拉索回归（Lasso Regression）：L1 正则化

逻辑回归

Sigmoid 函数

损失函数：交叉熵

K-means算法

聚类算法与分类算法

k-means算法

欠拟合、过拟合

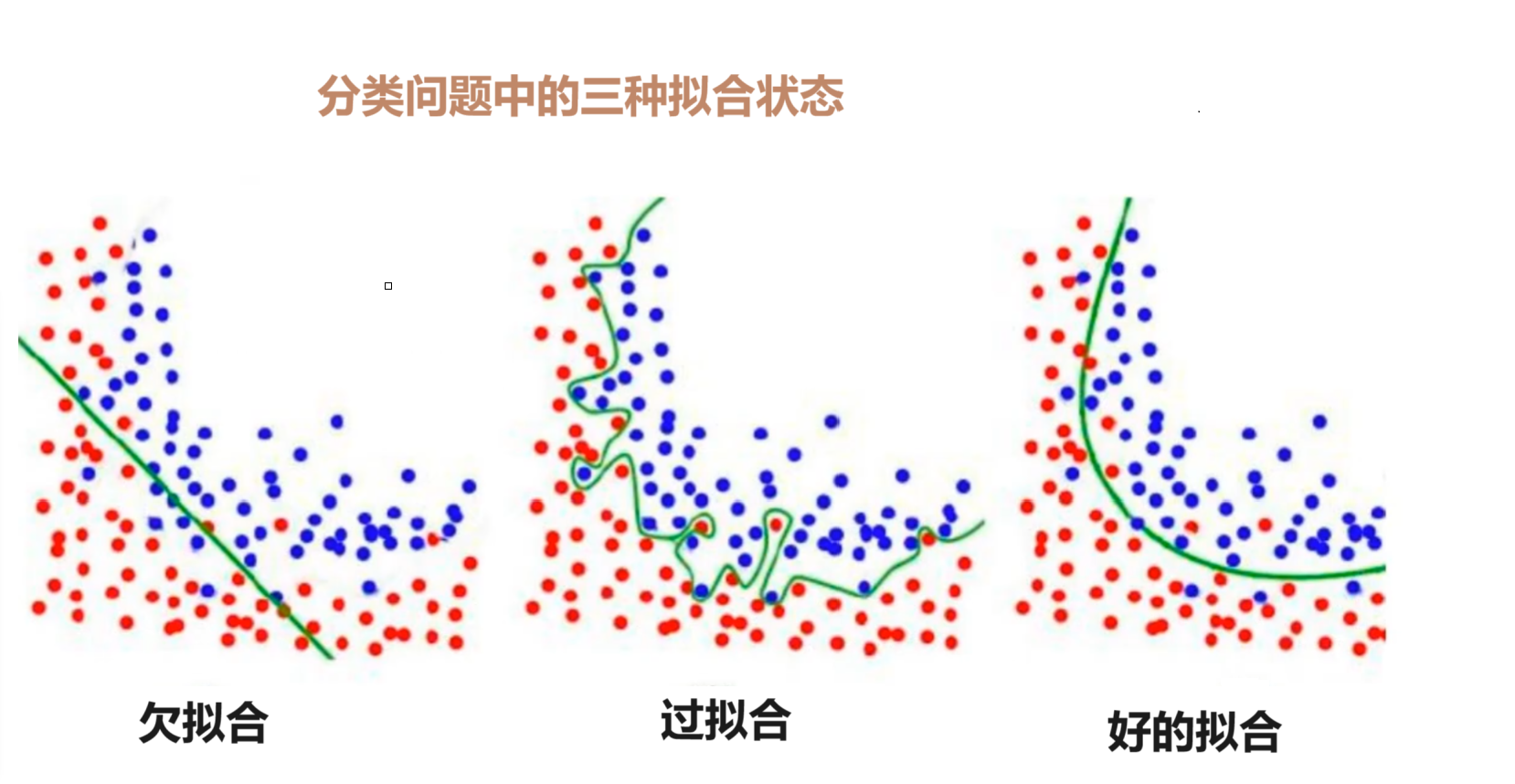
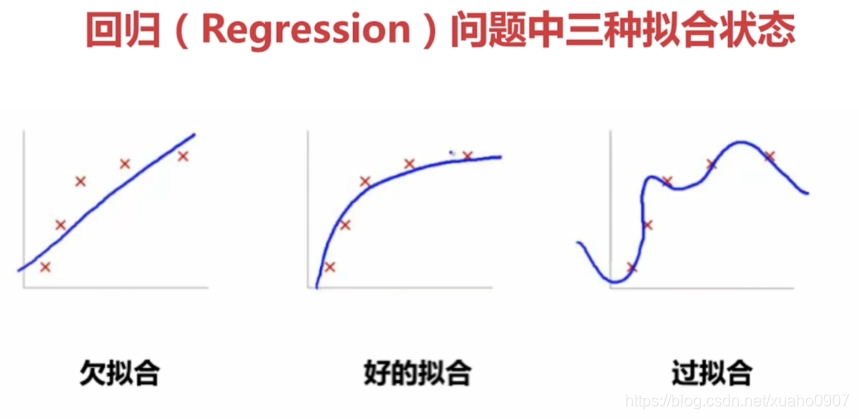
欠拟合

模型无法捕捉训练数据中的潜在模式和规律，导致在训练集和测试集上表现都很差（误差都很高）。

产生原因

模型过于简单：例如用线性模型拟合非线性关系（如房价与面积的关系可能是二次曲线，但用一次函数拟合）。
特征不足：输入特征太少，无法描述数据的关键规律（如预测房价只考虑面积，忽略地段、楼层等重要特征）。
正则化过度：对模型参数的惩罚太强，导致模型被过度简化。

过拟合

模型过度学习训练数据中的细节（包括噪声和随机波动），导致在训练集上表现极好，但测试集上表现很差（泛化能力差）。

产生原因

模型过于复杂：例如用 10 次多项式拟合本应是线性分布的数据。
训练数据不足或有噪声：样本量少，模型容易记住每个样本的细节（包括噪声）；数据中噪声多，模型会学习这些 “错误信息”。
特征过多：特征维度远大于样本量，模型容易找到巧合的特征组合拟合训练数据。

正则化

在机器学习中，模型训练的目标是 “既拟合训练数据，又能泛化到新数据”。但当模型复杂度过高时，容易出现过拟合（Overfitting）：

模型在训练集上表现极好（损失极低），但在测试集上表现很差（损失骤升）；
本质原因是模型 “记住” 了训练数据中的噪声和细节，而不是学习到通用规律。

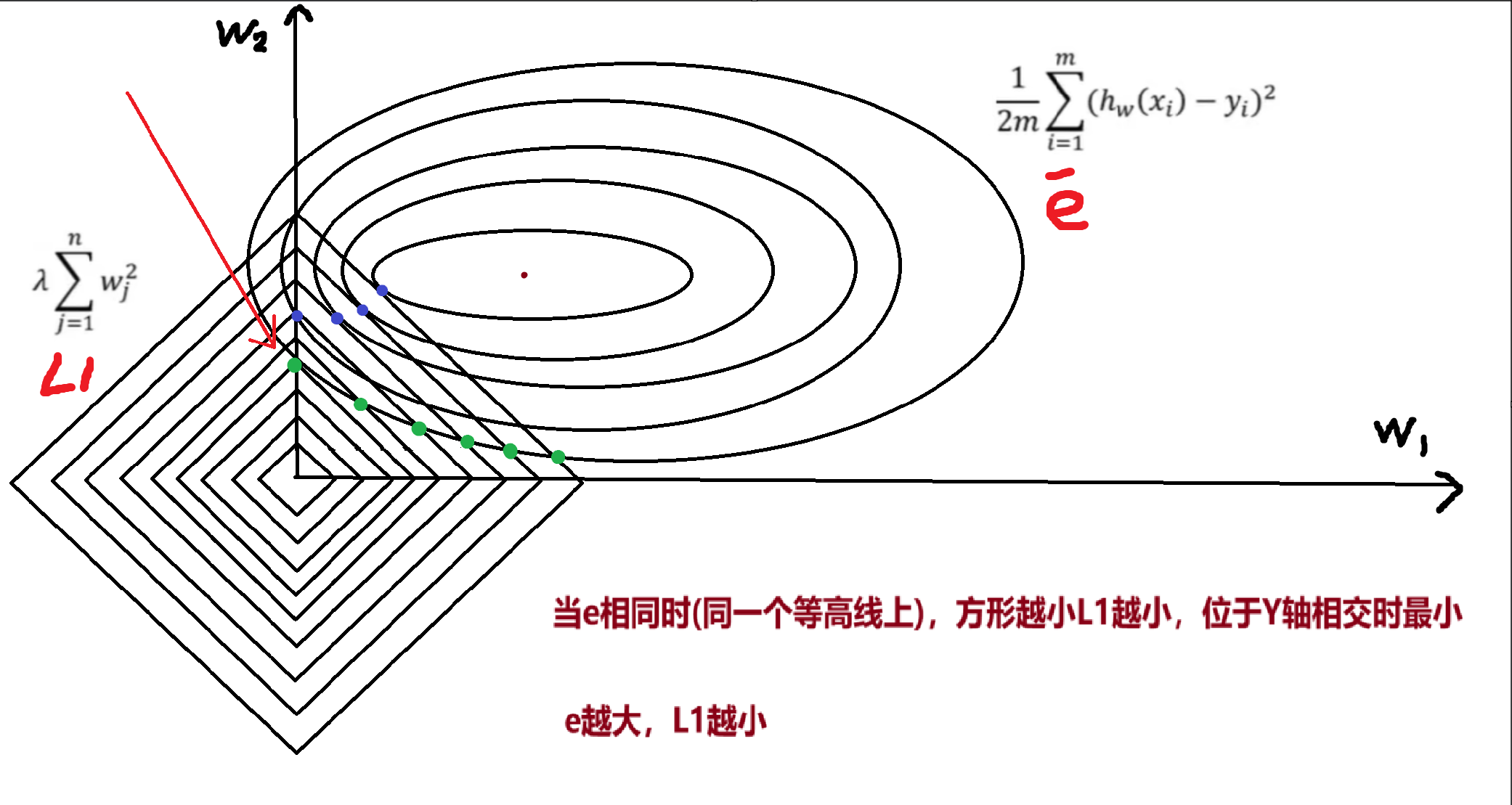
正则化的核心作用：通过在损失函数中加入 “参数惩罚项”，限制参数的取值范围（避免过大），降低模型复杂度，强制模型学习更简单、更稳定的规律，从而缓解过拟合。

正则化的数学本质是修改损失函数，在原始损失（如均方误差 MSE、交叉熵）的基础上，增加一个 “惩罚项”，形式如下：

正则化损失 = 原始损失 + $\lambda$ $\times$ 惩罚项

其中：

λ（正则化强度）：控制惩罚力度。λ=0时无正则化（可能过拟合）； λ越大，惩罚越强（参数被限制得越严格，模型越简单，可能欠拟合）。
惩罚项：根据形式不同，分为 L1 正则化和 L2 正则化（对应拉索回归和岭回归）。

岭回归（Ridge Regression）：L2 正则化

岭回归是线性回归的改进版本，通过引入L2 正则化解决过拟合问题，适用于特征间存在相关性的场景。

核心思想：在线性回归的损失函数中加入参数平方和的惩罚项，限制参数的 “大小”，避免参数因过度拟合噪声而变得过大。

$L2=||w||_2=\textstyle\sqrt[p]{\sum_{i=1}^{n}x^p_i,X=(x_1,x_2,...x_n)}$ 对应欧氏距离

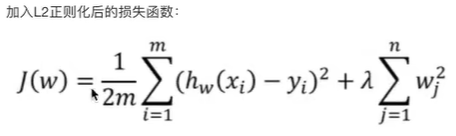
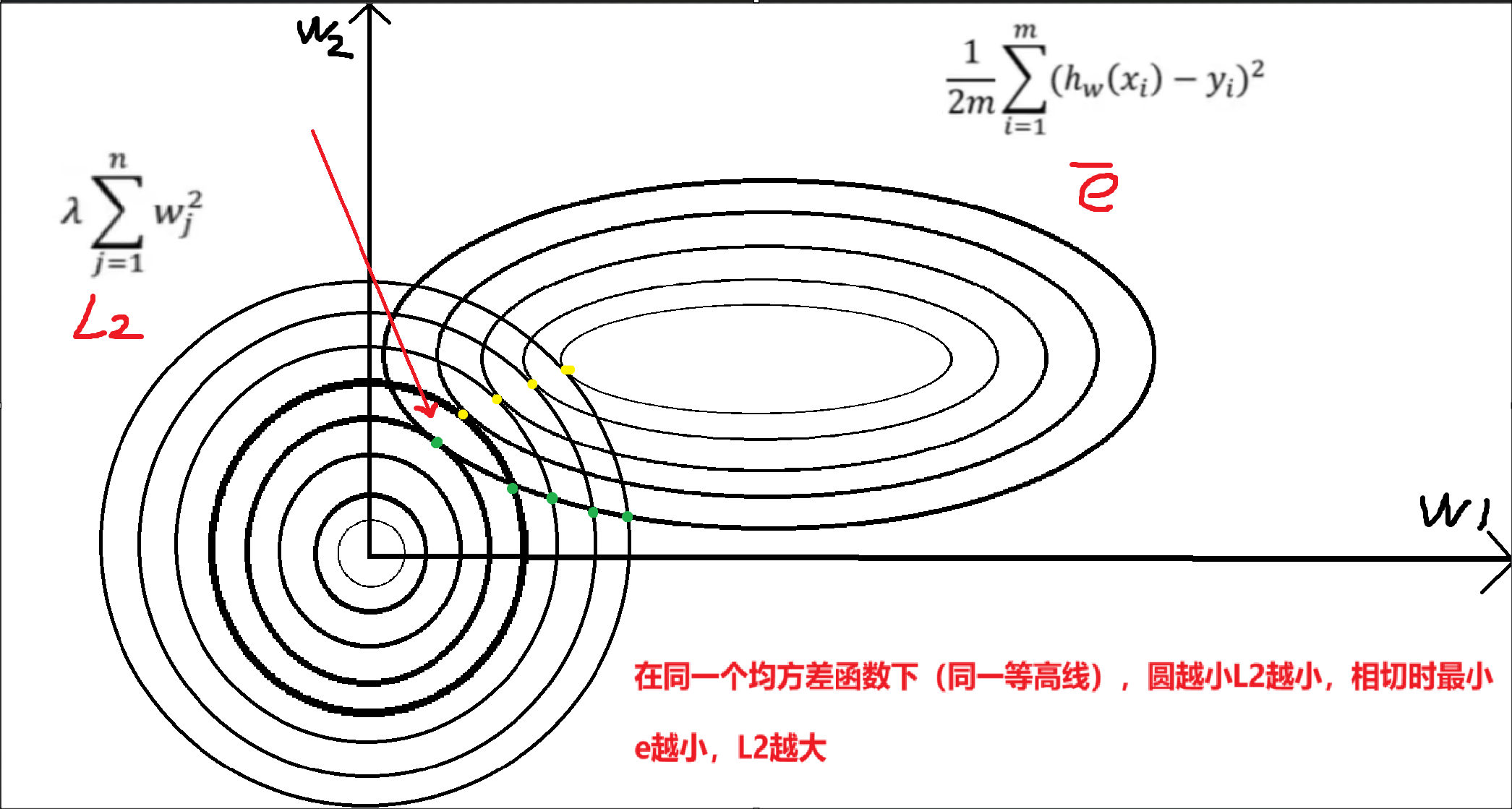
当λ增大时，为了使总损失最小，w的值变小（但不会变为 0）。
参数变小后，特征对预测结果的影响更温和，避免了个别特征的微小波动导致预测结果剧烈变化（模型更稳定）；
对于共线性特征（如高度相关的两个特征），L2 会让它们的权重 “平均分配”，避免某一个特征的权重过大。

适用场景

特征间存在较强相关性（如多重共线性问题）。
需要保留所有特征（不希望任何特征被完全剔除）。
样本量较少或特征维度较高的场景。

API

sklearn.linear_model.Ridge

alpha：正则化强度（λ），值越大惩罚越强。默认 1.0
fit_intercept：是否计算截距（w₀）。默认 True
max_iter：迭代最大次数
tol：收敛阈值，损失下降小于该值时停止。
属性：
- coef_：模型权重（w₁, w₂, ..., wₖ）
- intercept_：截距（w₀）

from sklearn.linear_model import Ridge
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error

X, y = fetch_california_housing(return_X_y=True,data_home = '../src')
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
scaler =  StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# 岭回归
# tol: 设置停止迭代的阈值
model = Ridge(alpha=0.1,max_iter=1000,fit_intercept=True,tol=0.1)
model.fit(X_train, y_train)

y_hat = model.predict(X_test)
print('w:',model.coef_)
print('b:',model.intercept_)
print('loss:',mean_squared_error(y_test, y_hat))

拉索回归（Lasso Regression）：L1 正则化

岭回归是线性回归的改进版本，通过引入L2 正则化解决过拟合问题，适用于特征间存在相关性的场景。

核心思想：在线性回归的损失函数中加入参数绝对值和的惩罚项，不仅限制参数大小，还会将不重要特征的参数 “压缩为 0”，实现特征选择。

$L1=||w||_1=\textstyle\sum_{i=1}^{n}|w_i|$ 对应曼哈顿距离

Lasso回归的目标是最小化以下损失函数：

$\text{J(w)}= \frac{1}{2n}\sum_{i=1}^n (h_w(x_i)-y_i)^2 + \lambda \sum_{j=1}^p |w_j|$

L1 惩罚项的特殊性质是会使部分参数变为 0（稀疏性）
当λ足够大时，不重要的特征的权重会被压缩到 0，相当于模型自动 “剔除” 了这些特征；
剩余的非零参数对应更重要的特征，模型复杂度显著降低（特征更少），从而缓解过拟合。

适用场景

高维稀疏数据（特征数量远大于样本量，如文本分类中的词袋特征）。
需要自动筛选特征（减少特征维度，简化模型）。
特征间相关性较低的场景（若特征高度相关，L1 可能随机剔除其中一个）。

API

sklearn.linear_model.Lasso

max_iter：迭代次数（L1 收敛较慢，通常需要更大值）
warm_start：是否利用上一次训练结果加速本次训练。默认 False
alpha：正则化强度，值越大惩罚越强
属性：
- coef_：模型权重（含 0 值，实现特征选择）
- intercept_：截距

from sklearn.linear_model import Lasso
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error

X, y = fetch_california_housing(return_X_y=True,data_home = '../src')
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
scaler =  StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# 岭回归
# tol: 设置停止迭代的阈值
model = Lasso(alpha=0.1,max_iter=1000,fit_intercept=True,tol=0.1)
model.fit(X_train, y_train)

y_hat = model.predict(X_test)
print('w:',model.coef_)
print('b:',model.intercept_)
print('loss:',mean_squared_error(y_test, y_hat))

逻辑回归

逻辑回归（Logistic Regression）是一种广泛应用于分类问题的统计学习方法，多用于解决二分类（或多分类）问题。它通过 Sigmoid 函数将线性回归的输出映射到 [0,1] 区间，从而表示样本属于某一类别的概率。

线性回归: $h(w)=w_1x_1+w_2x_2+....+b$

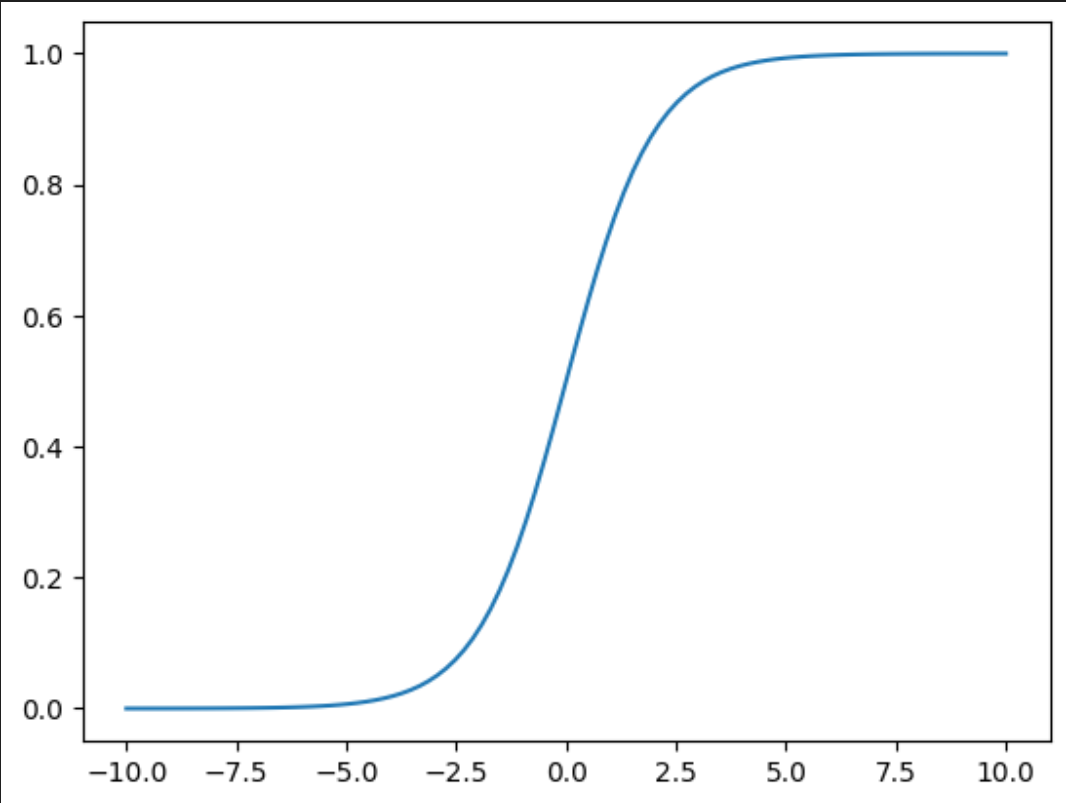
Sigmoid 函数

将线性回归的输出映射到 [0,1] 区间，从而表示样本属于某一类别的概率。

sigmoid激活函数 : $f(x)=\frac{1}{1+e^{-x}}$

把上面的h(w) 线性的输出再输入到sigmoid函数当中 $f(w)=\frac{1}{1+e^{-h(w)}}$

若f(w)> 0.5，预测为正类（1）
若f(w)< 0.5，预测为负类（0）

损失函数：交叉熵

逻辑回归不使用 MSE 作为损失函数（非凸函数，易陷入局部最优），而是使用交叉熵损失：

对于二分类问题，损失函数:

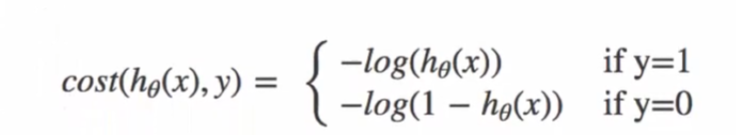
损失函数图:

当y=1时:

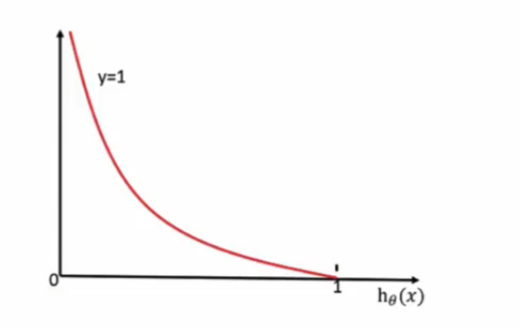
通过损失函数图像,我们知道:

当y=1时,我们希望 $h\theta(x)$ 值越大越好

当y=0时,我们希望 $h\theta(x)$ 值越小越好

综合0和1的损失函数:

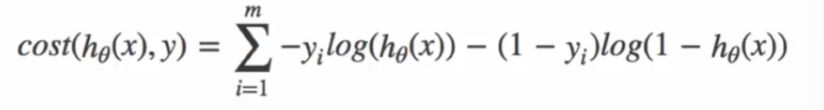
若 $y_i=1$ ，损失简化为−log(y^i)，y_hat 越接近 1，损失越小
若 $y_i$ =0，损失简化为 -log(1-y^i_hat))：y_hat 越接近 0，损失越小

手动算一下下:

API

sklearn.linear_model.LogisticRegression

penalty：正则化类型：'l2'（默认）、'l1'、'elasticnet'（L1+L2）、'none'
C ：正则化强度的倒数 C = 1/ λ ，值越小正则化越强。默认 1.0
max_iter：最大迭代次数（确保收敛）
属性：
- coef_：特征权重
- intercept_：截距
- predict_proba(X)：返回每个样本的类别概率

from sklearn.preprocessing import StandardScaler
from sklearn.feature_extraction import DictVectorizer
from sklearn.linear_model import LogisticRegression
import pandas as pd
from sklearn.model_selection import train_test_split


data = pd.read_csv('../src/titanic/titanic.csv')
print(data.to_numpy().shape)
# 列
# print(data.columns)

# 加载泰坦尼克号数据集，提取了三个特征：船舱等级 (pclass)、年龄 (age) 和性别 (sex)
y = data['survived'].values
x = data[['pclass', 'age', 'sex']]
# print(x.shape)
# print(x.head())



# 缺失值处理
# 对年龄中的缺失值使用平均值进行填充
x['age'].fillna(x['age'].mean(), inplace=True)
# 转换为字典格式，便于特征向量化
x = x.to_dict(orient='records')
# 字典向量化 转为矩阵
#sparse=False: 转为稠密矩阵
dicter = DictVectorizer(sparse=False)
x = dicter.fit_transform(x)
print("特征名称:", dicter.get_feature_names_out())
print("前10条处理后的特征:\n", x[:10])



scaler = StandardScaler()
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2,random_state=0)
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)
# 逻辑回归
model = LogisticRegression(max_iter=1000,fit_intercept=True)

# 训练
model.fit(x_train,y_train)

# 准确率
score = model.score(x_test,y_test)
print('score:',score)

(1313, 11)
特征名称: ['age' 'pclass=1st' 'pclass=2nd' 'pclass=3rd' 'sex=female' 'sex=male']
前10条处理后的特征:[[29.      1.      0.      0.      1.      0.    ][ 2.      1.      0.      0.      1.      0.    ][30.      1.      0.      0.      0.      1.    ][25.      1.      0.      0.      1.      0.    ][ 0.9167  1.      0.      0.      0.      1.    ][47.      1.      0.      0.      0.      1.    ][63.      1.      0.      0.      1.      0.    ][39.      1.      0.      0.      0.      1.    ][58.      1.      0.      0.      1.      0.    ][71.      1.      0.      0.      0.      1.    ]]
score: 0.8365019011406845

K-means算法

聚类算法与分类算法

在机器学习中，聚类算法（如 K-means）和分类算法是两类重要但本质不同的算法，核心区别在于是否依赖带标签的数据（监督 vs 无监督）。

分类算法：基于已有标签的训练数据，学习输入特征到输出类别的映射关系，新样本到来时直接应用该映射预测类别。

聚类算法：无需标签，仅根据样本间的相似度（如距离）自动划分成若干簇，使簇内样本相似、簇间样本差异大。

维度	聚类算法（如 K-MEANS）	分类算法
学习方式	无监督学习（数据无标签，无需人工标注）	监督学习（数据有标签，需已知类别）
目标	发现数据中隐藏的自然分组（簇），使组内相似度高、组间差异大	学习标签与特征的映射关系，预测新数据的类别
数据要求	仅需特征数据（X）	需特征数据（X）+ 标签（y）
典型应用	客户分群、异常检测、基因聚类	垃圾邮件识别、疾病诊断、图像分类

k-means算法

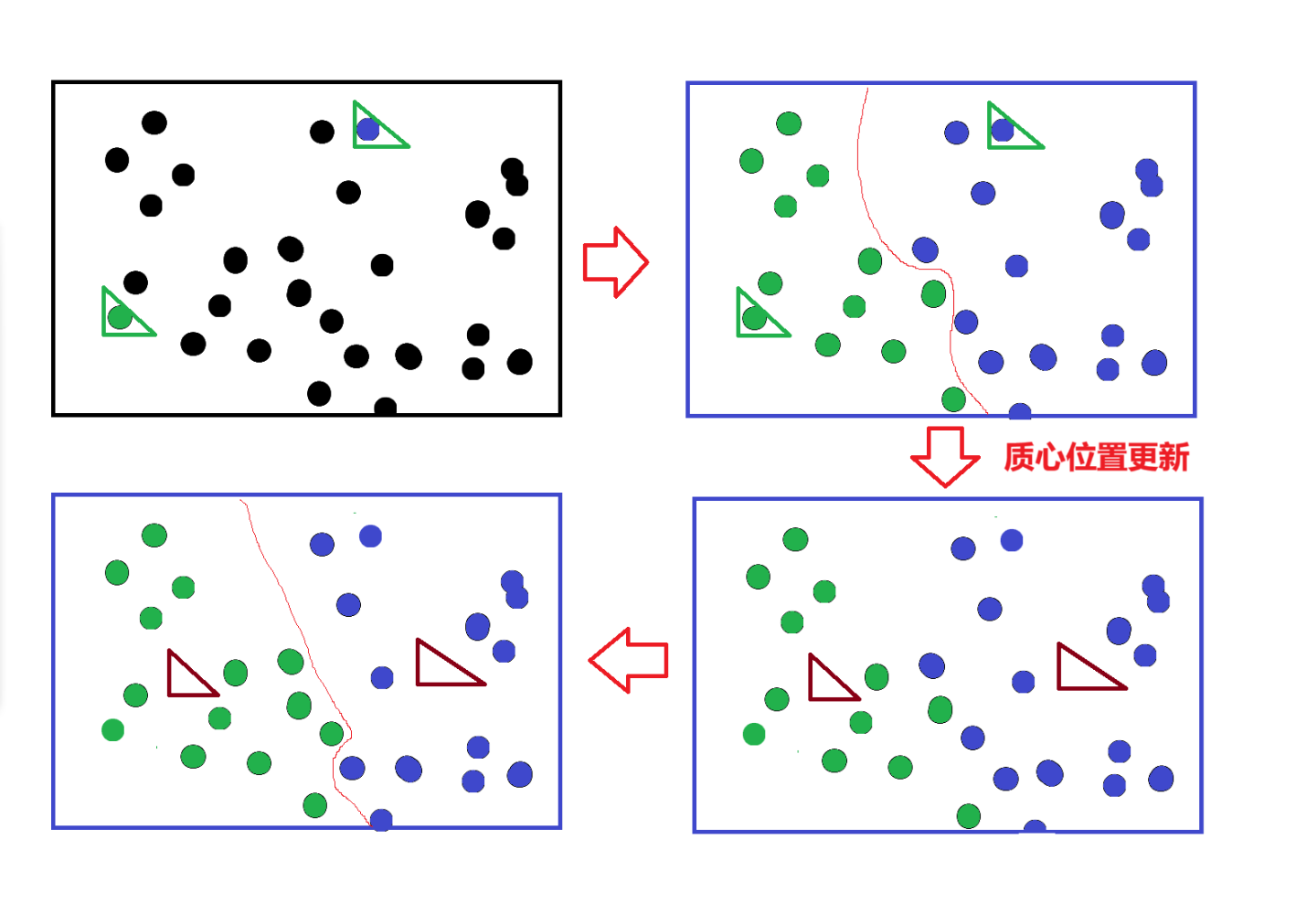
K-means 是一种无监督学习算法，用于将数据集划分为K个不同的簇（cluster）。其核心思想是：通过迭代寻找K个簇的 "中心"（质心），使每个样本点都属于与其最近的质心所在的簇，最终实现 "簇内相似度高、簇间相似度低" 的聚类效果。

K-means 中的 "K" 代表预设的簇数量（需要人工指定），"means" 指每个簇的质心是该簇内所有样本的均值。

K-means 的工作流程可概括为以下 4 个步骤，通过迭代优化直至收敛：

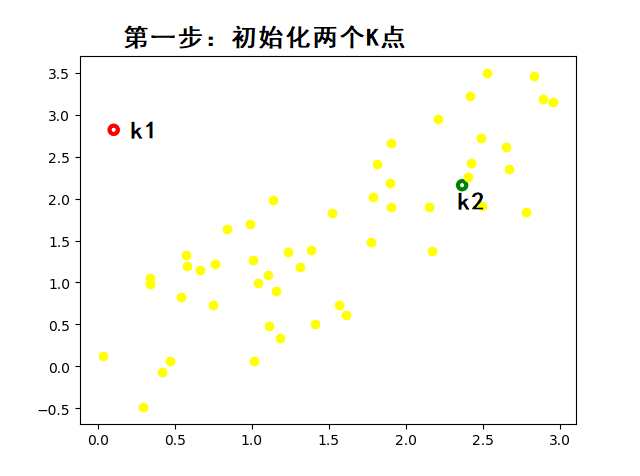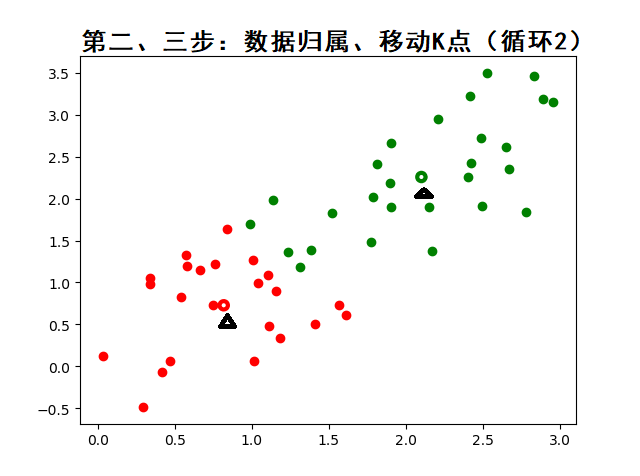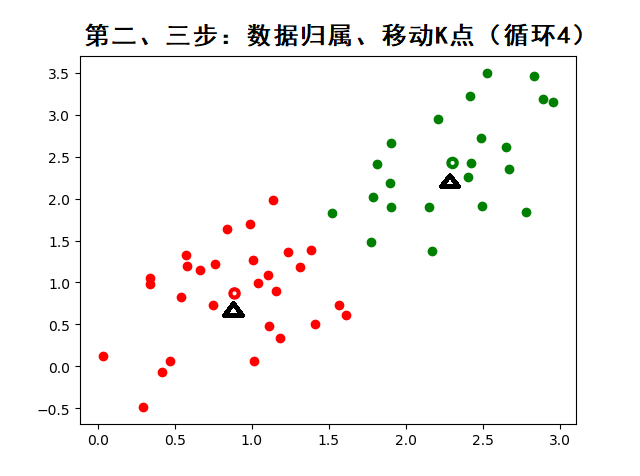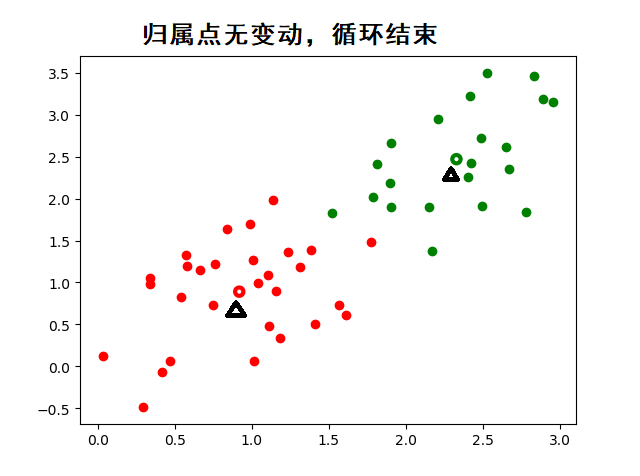
初始化：选择 K 个初始质心
- 随机从数据集中选择K个样本作为初始质心（早期方法）。
- 现代 K-means（如 sklearn 默认的k-means++）会优化初始质心选择：使初始质心之间的距离尽可能远，减少对最终结果的影响。
分配样本：将每个样本分配到最近的质心
- 计算每个样本与K个质心的距离（默认欧氏距离），将样本划分到距离最近的质心所在的簇。
- 此时每个簇的成员已确定。
更新质心：重新计算每个簇的质心
- 对每个簇，计算其内部所有样本的均值（坐标平均值），将该均值作为新的质心。
迭代收敛：重复步骤 2 和 3
- 当质心的位置变化小于某个阈值（如tol参数），或达到最大迭代次数（max_iter）时，停止迭代。
- 最终得到K个稳定的簇及对应的质心。

API

sklearn.cluster.KMeans类

n_clusters：指定聚类的数量 K（必填）。
init：初始质心的选择方式：
- 'k-means++'（默认）：智能选择初始点，避免随机初始化的弊端。
- 'random'：随机选择初始质心。
- 数组：手动指定初始质心。
n_init：运行算法的次数（每次使用不同初始质心），默认 10，最终选择最优结果。
max_iter：单次运行的最大迭代次数，默认 300。
random_state：随机种子，用于复现结果。
属性：
- cluster_centers_：最终的质心坐标。
- labels_：训练数据的簇标签。
- inertia_：误差平方和（SSE），用于肘部法选择 K 值。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
np.random.seed(42)
# 生成数据集
data = np.random.randint(0,100,(250,2))
# 创建模型
model = KMeans(n_clusters = 3)
model.fit(data)
y_predict = model.predict(data)
# 可视化 
# c 参数用于指定每个点的颜色
plt.scatter(data[:,0],data[:,1],c=y_predict)
plt.show()
print('质心坐标：',model.cluster_centers_)
print('标签：',model.labels_)
print('误差平方和：',model.inertia_)