lumerical——布拉格光栅（2）
一、创建结构
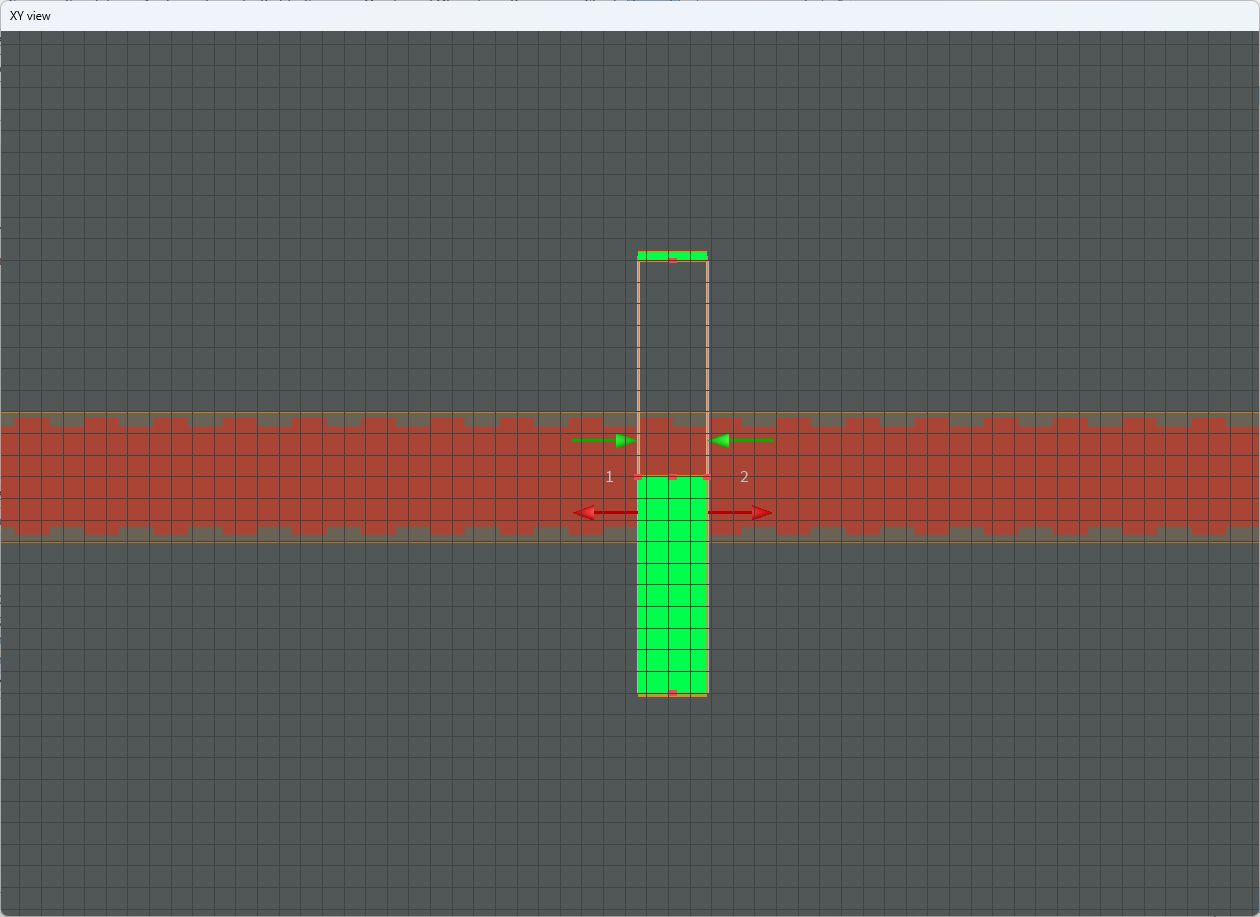
先创建波导
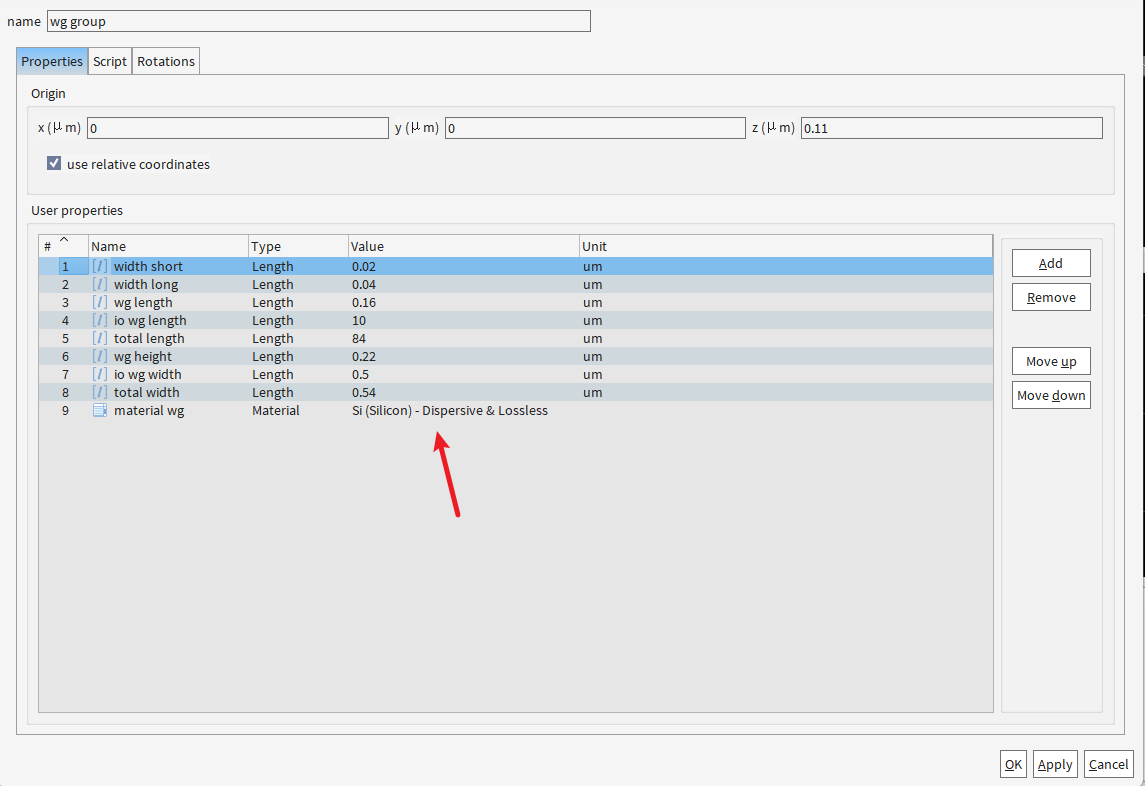
记得先给波导材料导入
为啥不用材料库原有的，要用这个？
色散模型（Dispersive）
该材料包含精确的波长相关折射率数据（如Sellmeier方程），能准确模拟硅在近红外波段（如1550nm）的色散特性。普通硅材料（如"Si - Silicon"）可能仅使用固定折射率（如n=3.48），导致以下问题：- 无法反映折射率随波长的变化（如1310nm vs 1550nm的折射率差异）
- 在宽光谱仿真（如超短脉冲）中会引入误差
无损耗假设（Lossless）
标签中的"Lossless"表示忽略硅的本征吸收损耗（适用于短距离器件仿真）。若需模拟损耗，应改用"Si (Silicon) - Dispersive & Lossy"。
deleteall;
um = 1e-6;
width_short = %width short%;
width_long = %width long%;
wg_length = %wg length%;
io_wg_length = %io wg length%;
total_length = %total length%;
wg_height = %wg height%;
io_wg_width = %io wg width%;
total_width = %total width%;
material_wg = %material wg%;period = wg_length * 2;
N = (total_length - io_wg_length*2) / period;addpoly;
set("material", material_wg);
set("name", "input_wg");
vertices = [-io_wg_length, -io_wg_width/2;0, -io_wg_width/2;0, io_wg_width/2;-io_wg_length, io_wg_width/2;-io_wg_length, -io_wg_width/2];
set("vertices", vertices);
set("z span", wg_height);for(i=1:N) {x_start = (i-1)*period;if(i == N){vertices = [x_start, -total_width/2;x_start+wg_length, -total_width/2;x_start+wg_length, -total_width/2+width_long;x_start+period, -total_width/2+width_long;x_start+period, -io_wg_width/2;x_start+period+io_wg_length, -io_wg_width/2;x_start+period+io_wg_length, io_wg_width/2;x_start+period, io_wg_width/2;x_start+period, total_width/2-width_long;x_start+wg_length, total_width/2-width_long;x_start+wg_length, total_width/2;x_start, total_width/2;x_start, -total_width/2];addpoly;set("material", material_wg);set("vertices", vertices);set("z span", wg_height);break;}vertices = [x_start, -total_width/2;x_start+wg_length, -total_width/2;x_start+wg_length, -total_width/2+width_long;x_start+period, -total_width/2+width_long;x_start+period, total_width/2-width_long;x_start+wg_length, total_width/2-width_long;x_start+wg_length, total_width/2;x_start, total_width/2;x_start, -total_width/2];addpoly;set("material", material_wg);set("vertices", vertices);set("z span", wg_height);}vertices = [vertices; N*period, -io_wg_width/2];
注：addpoly的vertices要注意首尾相连！
创建基底
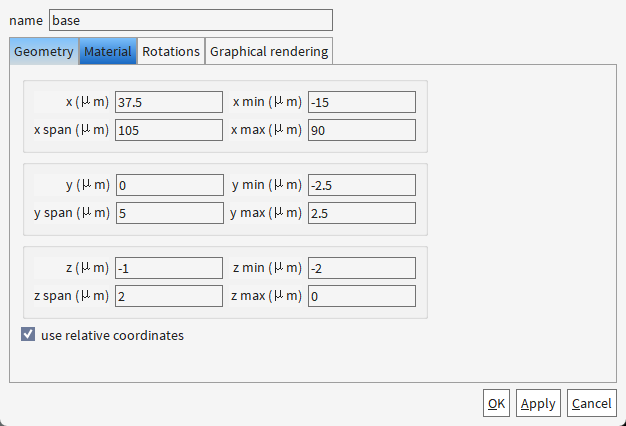
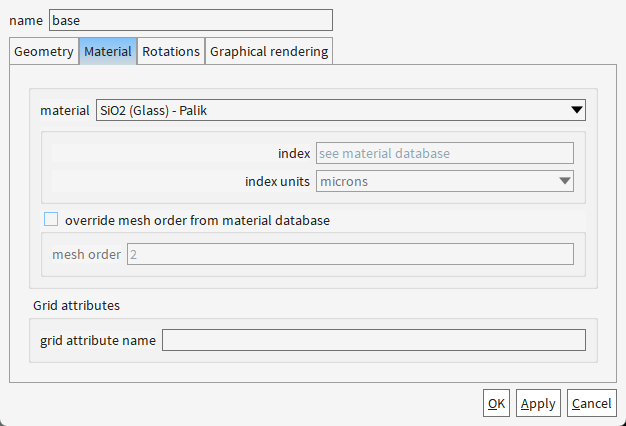
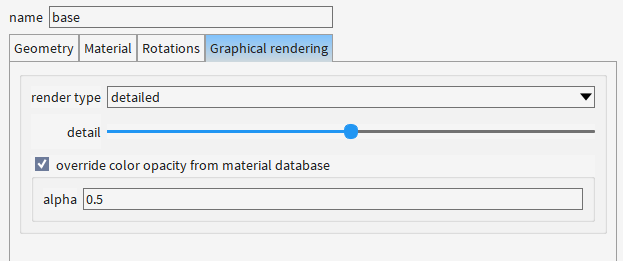
透明度0.5是为了方便观察波导
二、添加FDE
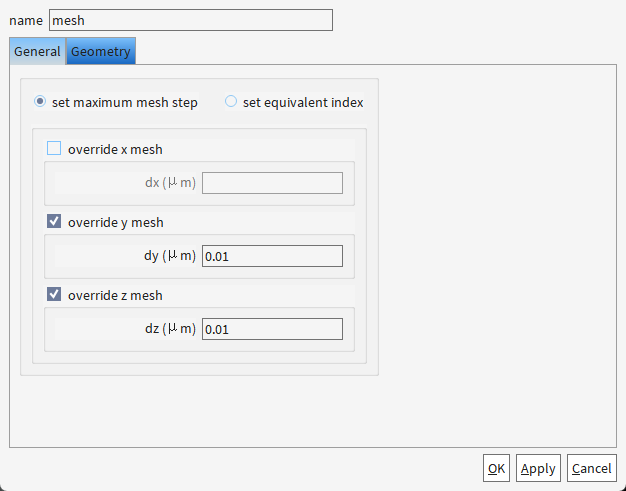
为啥dx不用重写？
物理意义：
- dy/dz 覆盖（0.01 μm）：通常用于波导截面（Y-Z平面）的精细剖分，确保模式场（如TE/TM模）在垂直方向的分辨率。例如：
- 硅波导高度（~220 nm）和宽度（~500 nm）需要亚纳米级网格（如0.01 μm）捕捉倏逝场。
- dx 未覆盖：在光传播方向（X轴），场变化较缓慢（如布拉格光栅周期为数百纳米），可采用默认的粗网格（如0.1 μm），以平衡精度与计算量。
- dy/dz 覆盖（0.01 μm）：通常用于波导截面（Y-Z平面）的精细剖分，确保模式场（如TE/TM模）在垂直方向的分辨率。例如：
仿真效率：
若光传播方向（X）无剧烈场变化（如均匀波导），覆盖dx会导致不必要的网格加密，显著增加计算时间，而对结果精度提升有限
注：网格尺寸应满足 Δ≤λ/(10n)，其中 n 为材料折射率
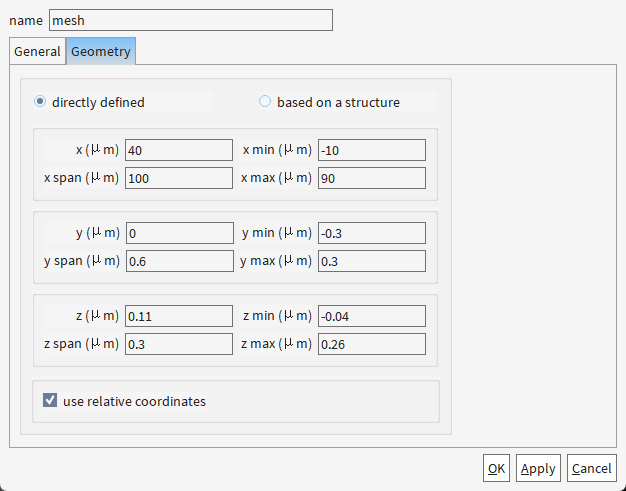
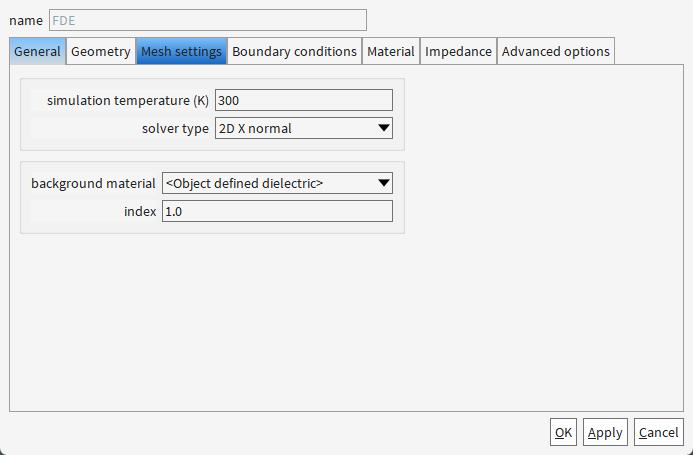
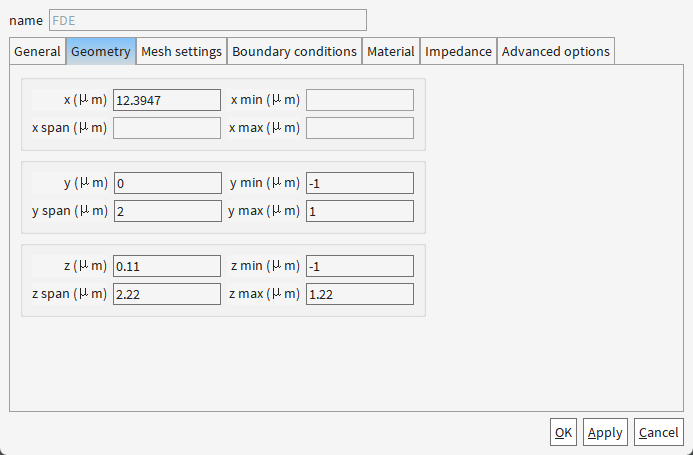这里需要注意的点：
（1）FDE所在的位置必须位于光栅的非扰动区（如齿间平坦处），避免模式畸变（若选在齿中心，neff会错误偏移），并且FDE的X坐标必须位于EME的仿真范围内！
（2）FDE的Y和Z，必须与EME的Y和Z完全一致！
- EME需继承FDE计算的模式场分布，必须保证两者在Y/Z截面的网格对齐。
- 若EME的Y/Z范围小于FDE，会截断模式场，导致传播仿真失真。
三、添加EME
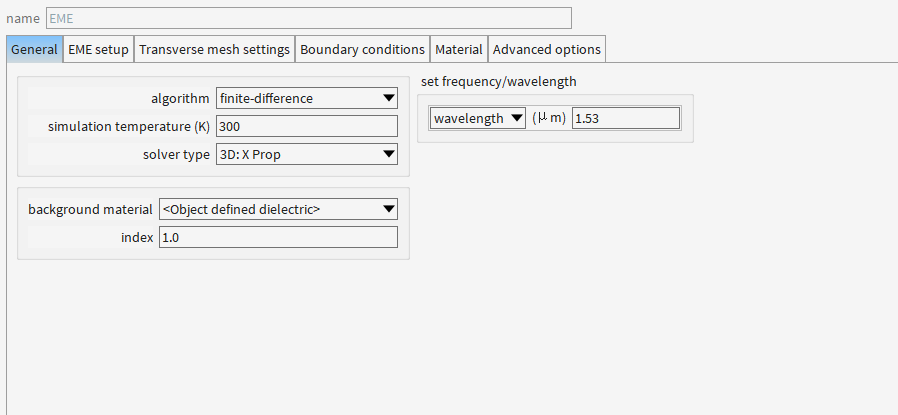
| 选项名称 | 维度与传播方向 | 物理意义 | 典型应用场景 | 计算效率 |
|---|---|---|---|---|
| 3D: X Prop | 三维全空间 + 沿X轴传播 | 完整计算Y-Z截面模式场，严格模拟X方向传播 | 布拉格光栅、三维波导、光子晶体 | 较高（需Y-Z网格加密） |
| 2D XY plane: X prop | 二维XY平面 + 沿X轴传播（忽略Z） | 假设Z方向无限均匀（∂E/∂z=0），仅分析XY平面模式 | 无限高平板波导、二维光子器件 | 高（比3D快5-10倍） |
| 2D XZ plane: X prop | 二维XZ平面 + 沿X轴传播（忽略Y） | 假设Y方向无限均匀（∂E/∂y=0），专注XZ平面特性（如衬底耦合） | 条形波导垂直耦合、倏逝场衰减分析 | 高（比3D快5-10倍） |
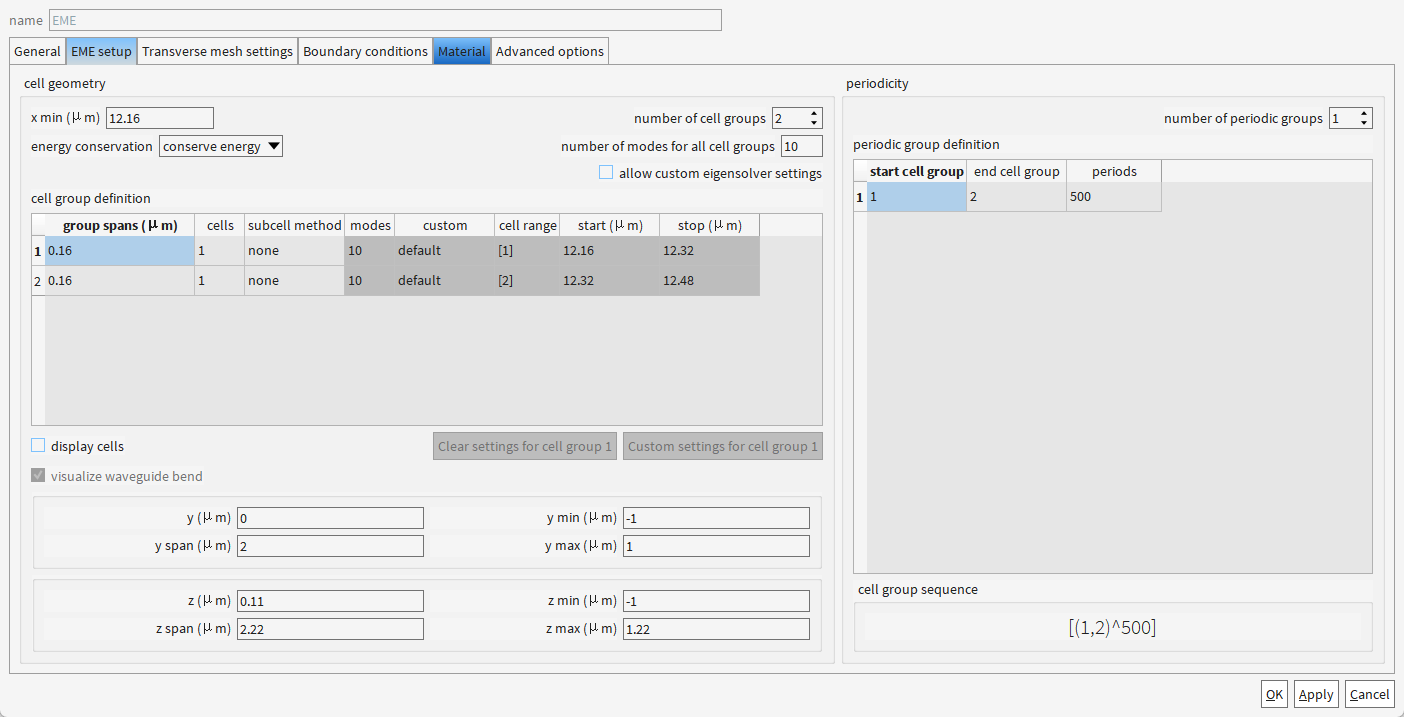可以看到，FDE的X坐标确实是在EME范围内，两者Y和Z完全一致
| 选项 | 作用 | 适用场景 |
|---|---|---|
| none | 不启用任何特殊处理，完全依赖物理模型计算 | 快速验证或调试时使用 |
| make passive | 强制系统为无源（忽略所有增益和损耗） | 分析无源器件（如硅基波导）或排除材料非线性干扰时 |
| conserve energy | 严格保证能量守恒（通过自动调整数值算法） | 高精度仿真（如谐振腔Q值计算）、需严格能量平衡的场景（默认推荐） |
conserve energy，这是默认推荐选项，尤其适用于布拉格光栅仿真（需精确计算反射/透射率）
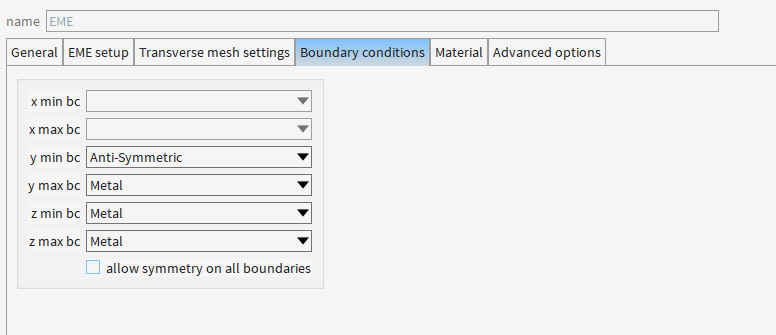
Anti-Symmetric ：强制电场在边界处满足反对称条件
软件会在Y=0边界（y min）自动镜像反转载荷，使场分布满足反对称性
四、添加参数扫描
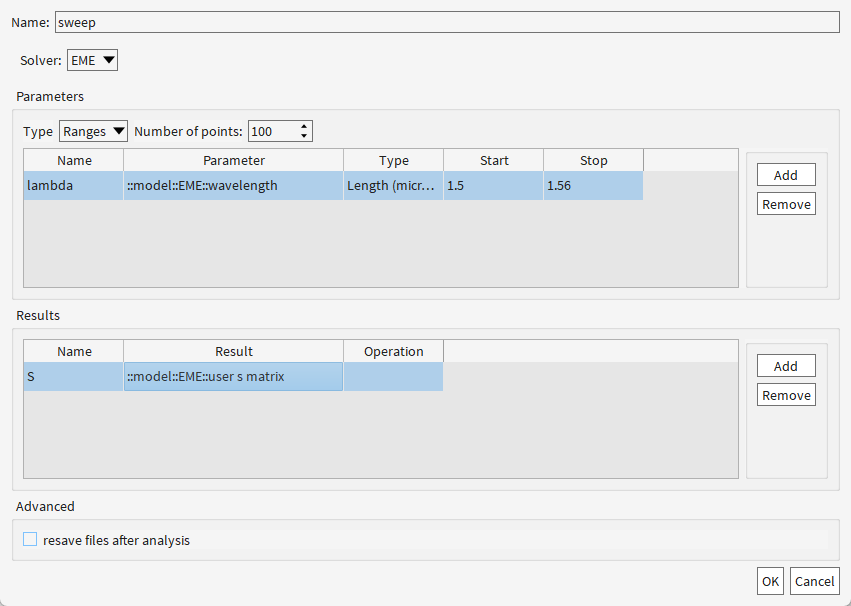
波长扫描仿真：
在 1.5 μm 到 1.56 μm 的波长范围内，以 100个均匀采样点 计算器件的S参数（反射/透射特性）。
五、运行
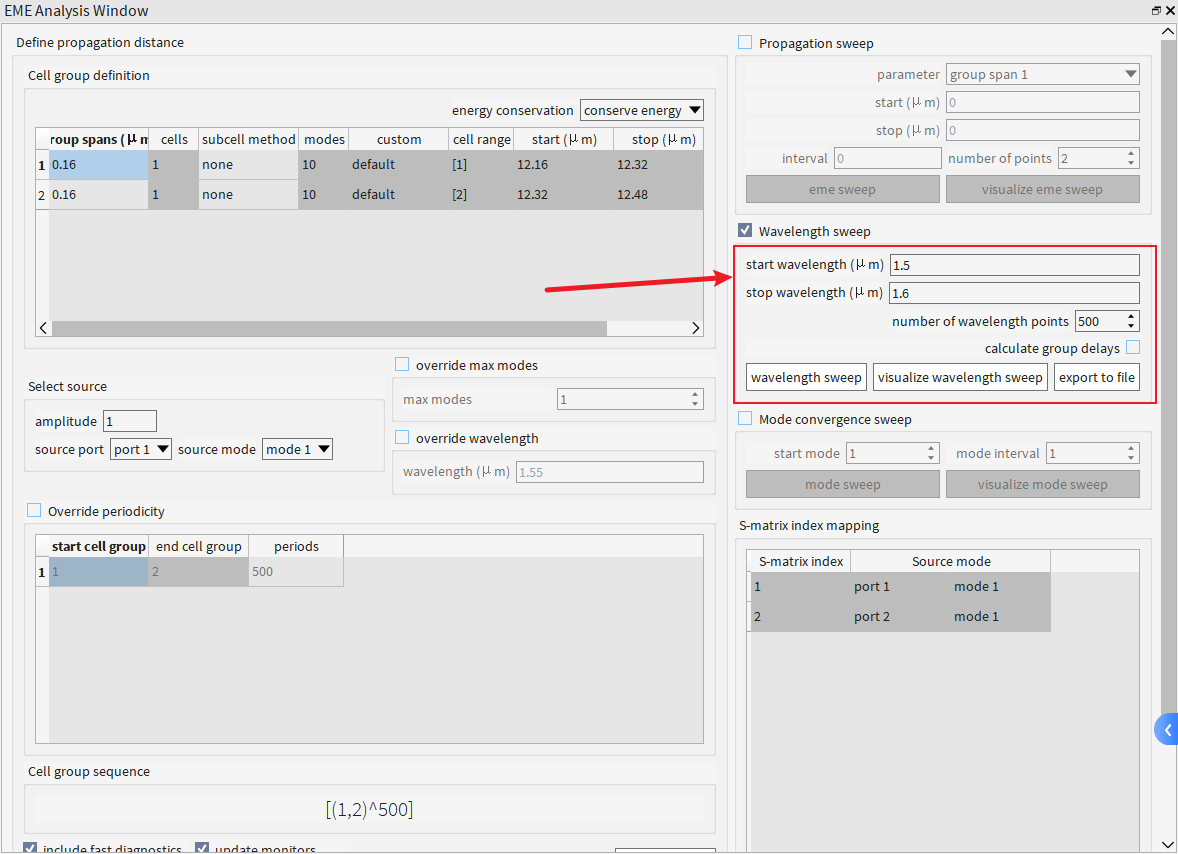
可在此处设置，这里我设置了扫描500个点
可将S11,S12,S22 remove即可
也可以用参数扫描扫，这个得多等待会
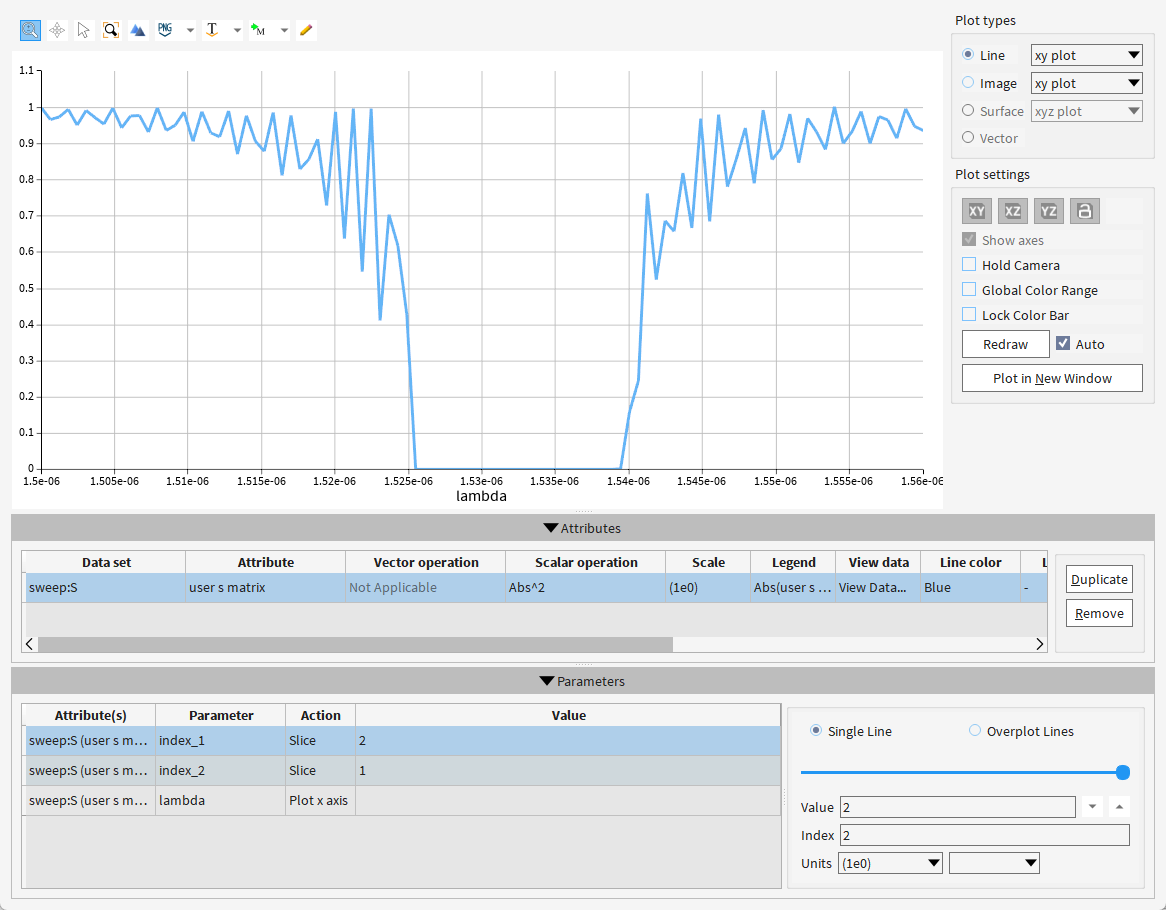
注意改一下parameters的值
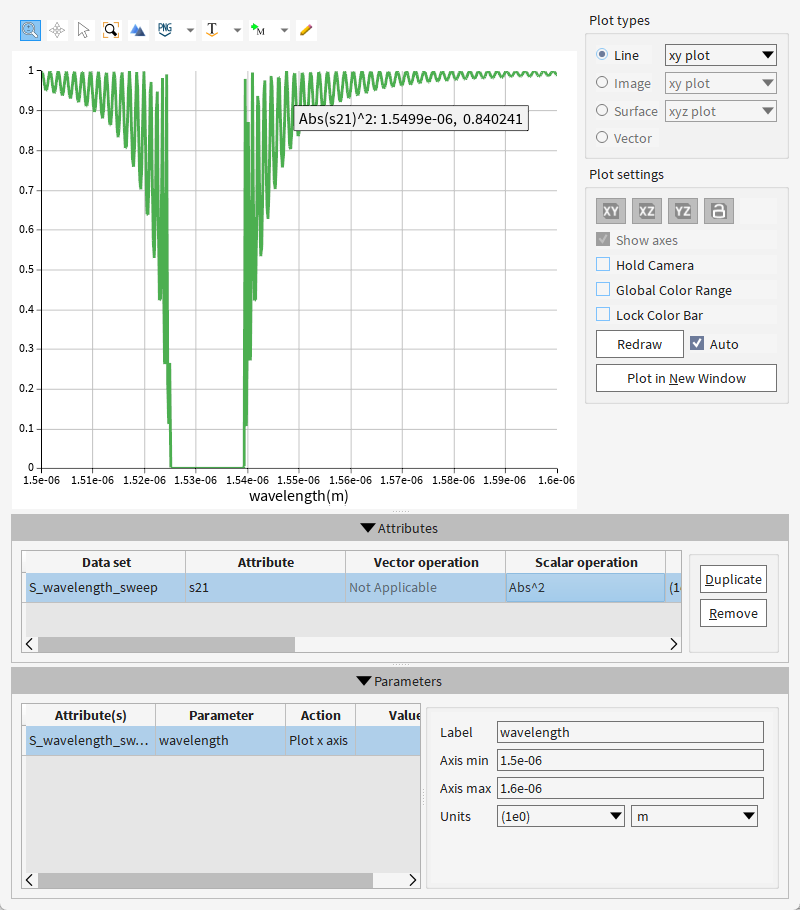
结果分析：
- 横轴：波长（1.5 μm ~ 1.6 μm）——覆盖光纤通信C波段（1530-1565 nm）
- 纵轴：归一化强度（0~1），通常表示 透射率（T）的平方绝对值（如∣S21|^2）
- 曲线特征：
- 在 1.53 μm 附近出现明显凹陷（最小值约0.1）
- 其他波长区域透射率较高（0.7~0.9）
凹陷位置（1.53 μm）：对应器件的 共振波长 或 阻带中心,满足布拉格条件 λBragg=2neffΛ（Λ为光栅周期）
凹陷深度：最小值0.1 → 表示该波长处 90%的光被反射/吸收
带宽：凹陷半高宽（FWHM）约 10 nm，反映器件的波长选择性
- 该器件在 1530 nm 处具有强反射/吸收特性，适合用作：
- 波长滤波器（隔离1530 nm信号）
- 激光器谐振腔的选频元件
曲线在1.52/1.54 μm处有小凹陷，说明存在高阶反射