Leetcode力扣解题记录--第238题(前/后缀积)
题目链接:238. 除自身以外数组的乘积 - 力扣(LeetCode)
题目描述
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
提示:
-
2 <= nums.length <= 105
-
-30 <= nums[i] <= 30
-
输入 保证 数组 answer[i] 在 32 位 整数范围内
题目作答
这个问题的核心限制是:不能使用除法,并且时间复杂度必须是 O(n)。
一个很巧妙的解法是利用前缀积和后缀积。对于数组中的任何一个位置 i,answer[i] 的值其实就是 i 左边所有元素的乘积,再乘以 i 右边所有元素的乘积。
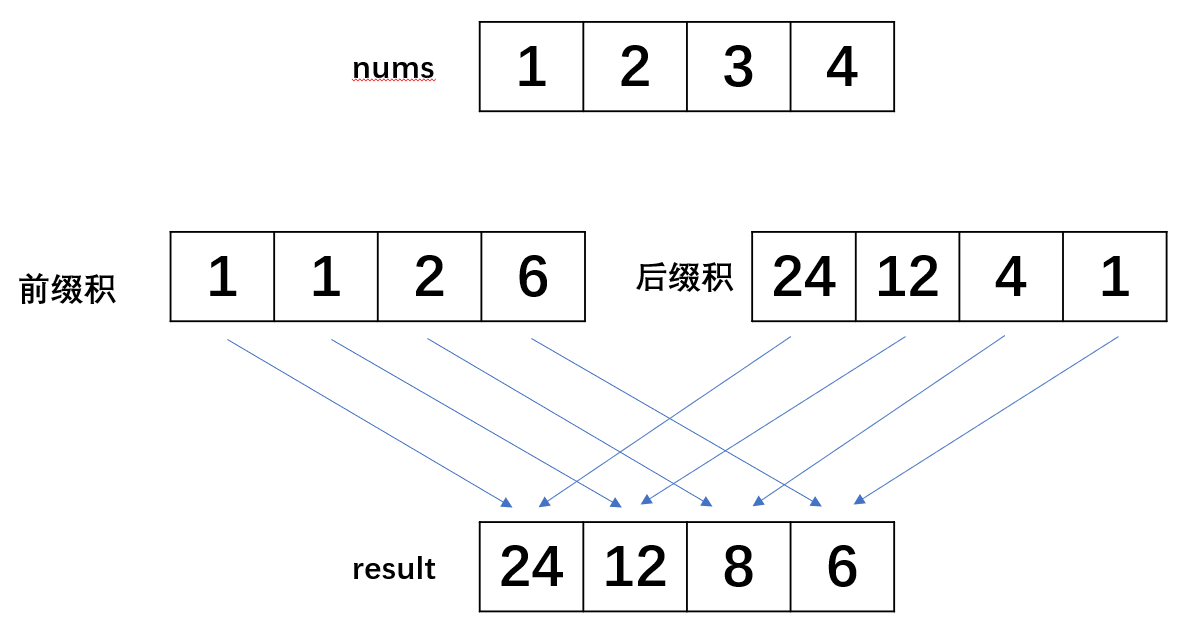
上图最终可以组合简化成为一个result数组,以上只是为了方便理解。
我们可以分两步来构建最终的 answer 数组:
-
第一步:计算前缀积
-
我们从左到右遍历数组。对于 answer[i],我们先计算 nums[i] 左侧所有元素的乘积。
-
为了实现这一点,我们可以让 answer[i] = nums[0] * nums[1] * ... * nums[i-1]。
-
我们可以用一个循环来完成:answer 数组的第一个元素 answer[0] 初始化为 1(因为 nums[0] 左边没有元素)。然后从 i=1 开始,answer[i] = answer[i-1] * nums[i-1]。
-
在这一步完成后,answer 数组的每个位置 i 存储的都是原数组 i 左侧所有元素的累积乘积。
-
-
第二步:计算后缀积并得出最终结果
-
现在 answer 数组里已经有了前缀积,我们还需要乘上后缀积。
-
我们从右到左遍历数组。我们用一个变量 suffix_product 来记录 nums[i] 右侧所有元素的乘积。这个变量初始值为 1。
-
在遍历到 i 时,我们先用 answer[i](目前存的是前缀积)乘以 suffix_product,这样就得到了最终结果,并更新 answer[i]。
-
然后,为了下一次迭代(i-1),我们需要更新 suffix_product,让它乘上当前的 nums[i]。
-
当这个从右到左的遍历结束后,answer 数组就包含了我们想要的所有结果。
-
通过这两次 O(n) 的遍历,我们用 O(n) 的总时间复杂度和 O(1) 的额外空间(不包括返回的 answer 数组)解决了这个问题,且没有使用除法。
class Solution {
public:// 函数名根据题目要求应该是 productExceptSelfvector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();// answer 数组用来存放最终结果vector<int> answer(n);// 步骤 1: 计算前缀积// answer[i] 先存储 nums[i] 左侧所有元素的乘积// 对于 answer[0],其左侧没有元素,所以是 1answer[0] = 1;for (int i = 1; i < n; i++) {answer[i] = answer[i - 1] * nums[i - 1];}// 步骤 2: 计算后缀积并与前缀积相乘// suffix_product 用于记录右侧所有元素的乘积// 初始化为 1,因为最右边元素的右侧没有元素int suffix_product = 1;for (int i = n - 1; i >= 0; i--) {// 对于位置 i,answer[i] 目前是左侧乘积// 再乘以右侧乘积 suffix_product,就是最终结果answer[i] = answer[i] * suffix_product;// 更新 suffix_product,为下一次迭代(i-1)做准备// 它的右侧乘积需要包含当前的 nums[i]suffix_product *= nums[i];}return answer;}
};