机器学习week3-分类、正则化
1. 逻辑回归
1.1. 线性回归 vs 逻辑回归
对比维度 | 线性回归 | 逻辑回归 |
任务类型 | 回归(预测连续值) | 分类(预测离散类别) |
输出范围 | (−∞,+∞) | [0,1](概率值) |
损失函数 | 均方误差(MSE) | 对数损失(交叉熵损失) |
假设条件 | 假设输出与特征呈线性关系 | 假设概率的对数几率与特征呈线性关系 |
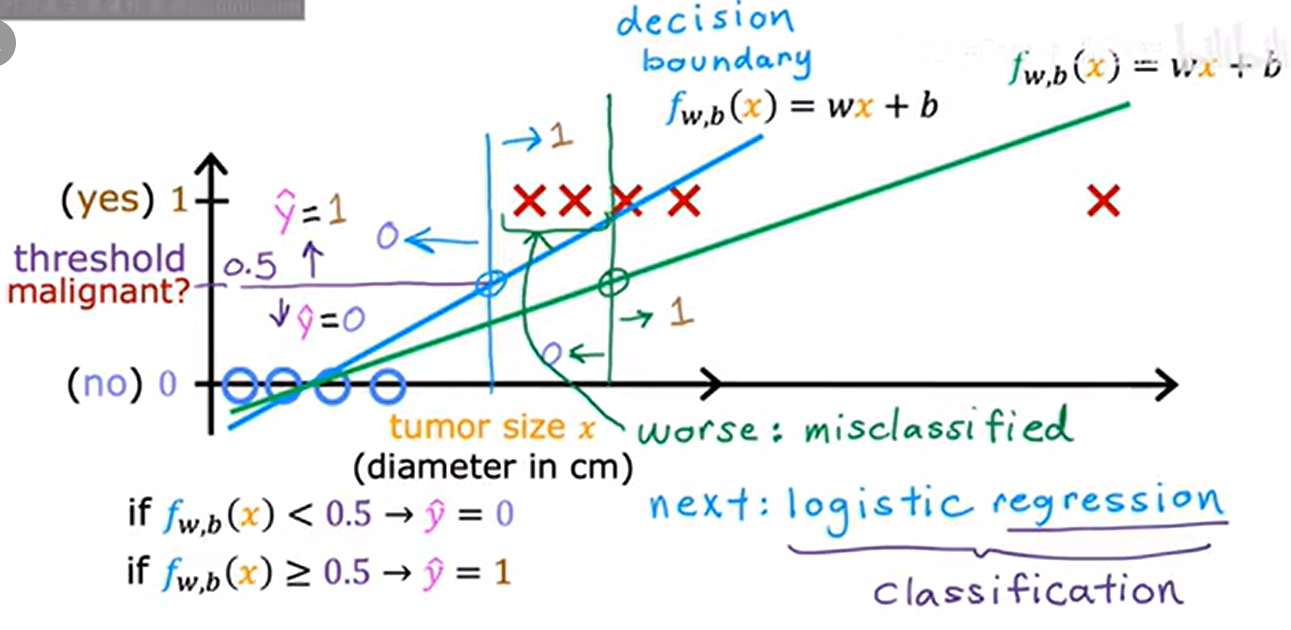
1.2. 场景:肿瘤分类
- X轴:肿瘤大小;Y轴:0-良性,-恶性
- 决策边界(decision boundary:由线性函数 (f_{w,b}(x) = wx + b) 定义,用于划分两个类别
- 决策边界及左边:0-良性,右边:1-恶性
在右边添加额外训练样本(肿瘤很大的样本)会导致线性函数发生偏移
- (蓝)线性函数变成(绿)线性函数;
- 决策边界也右移
- 原本为恶性的肿瘤样本预测为0-良性
- 显然错误,右边的样本不应该影响怎么分类良恶性的
- 添加新的样本,线性函数更差
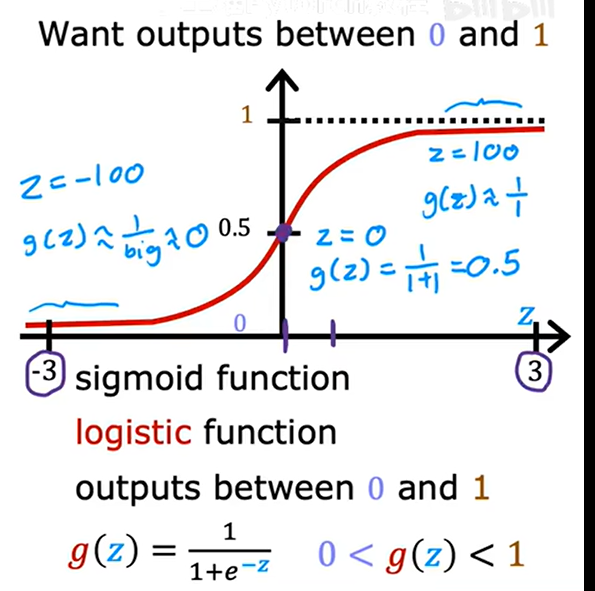
1.3. 逻辑函数
Logistic Function,也称为 Sigmoid 函数,S 形曲线函数。它将任意实数输入值映射到区间 (0, 1)。
g(x) =1/(1 + e^(-x))
- e 是自然常数(约等于 2.71828)
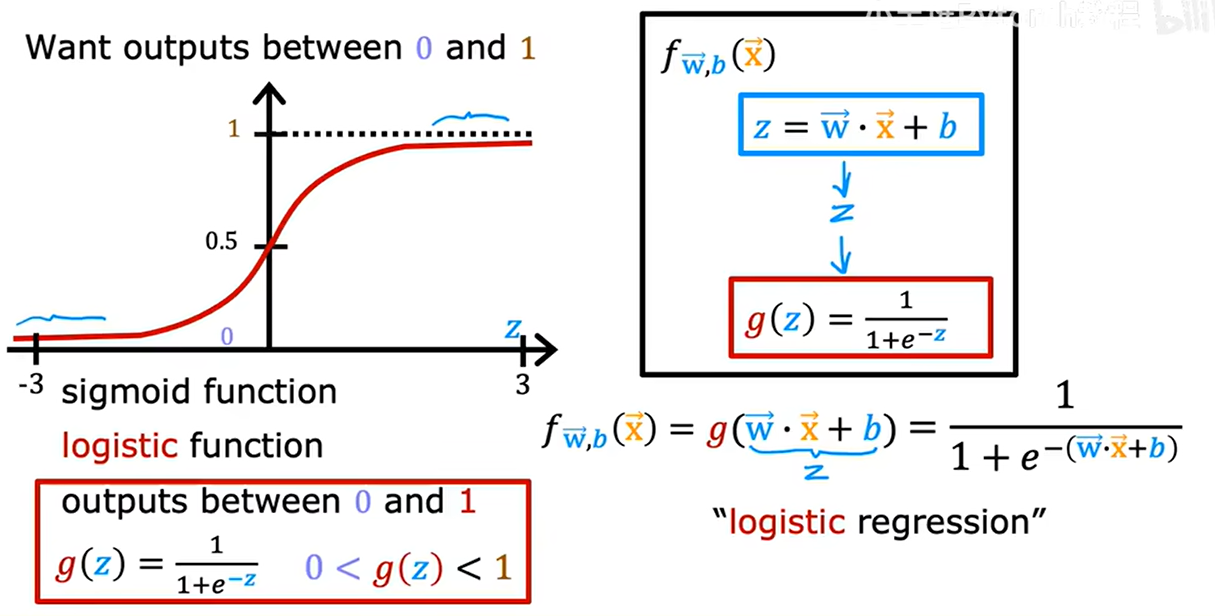
1.4. 构建逻辑回归算法
输入一个特征/一组特征x,输出一个(0,1)间的数字
- 定义z值:z= wx + b
- z值作为输入,带入到逻辑函数 g(z) =1/(1 + e^(-z)) 中
- 得到逻辑回归模型 f(x)=g(wx+b)
输出的理解:对于给定输入x值时,类别y=1的概率
- 肿瘤大小为x时,肿瘤为恶性的概率
2. 决策边界
z= wx + b ----> g(z) =1/(1 + e^(-z)) ------> f(x)=g(wx+b)
- f(x)>0.5时,表分类=1概率>0.5,分类=1;否则f(x)<0.5时,表分类=1概率<0.5,分类=0
- f(x)>0.5时,根据逻辑函数曲线图,z>0,z=wx+b
- wx+b>0时,z>0,f(x)>0.5,分类=1;wx+b<0时,z<0,f(x)<0.5,分类=0
- 决策边界:wx+b=0的线
有两个输入特征:x1、x2
- z=w1x1+w2x2+b
- f(x)=g(w1x1+w2x2+b)
- 决策边界:w1x1+w2x2+b=0
令w1=w2=1,b=-3
- z=x1+x2-3
- 决策边界:x1+x2=3
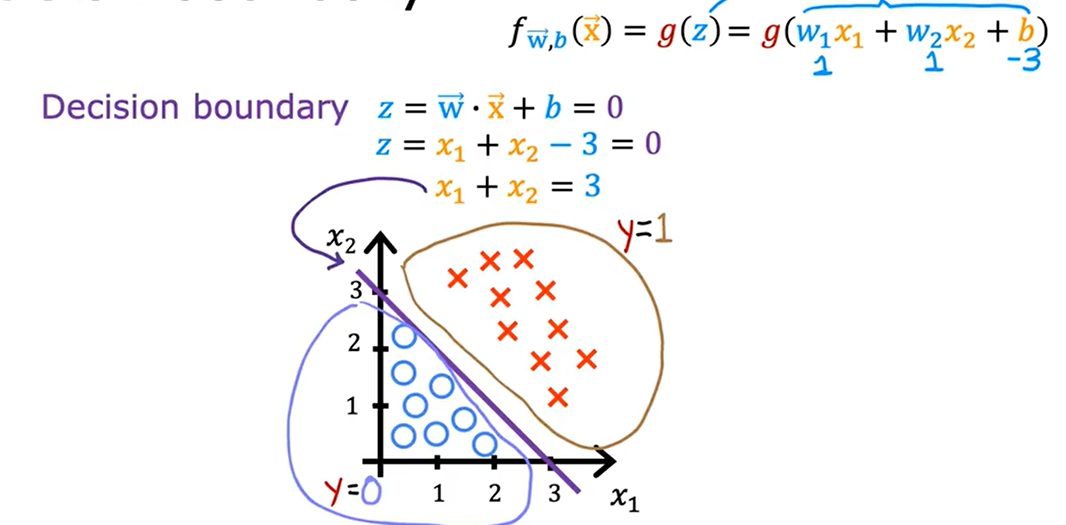
决策边界非直线
- 多项式特征:z=w1x1^2+w2x2^2+b
- 假设w1=w2=1,b=-1;z=x1^2+x2^2-1
- 决策边界:x1^2+x2^2=1
- 圆外:z>0,f(z)>0.5,分类y=1
- 圆内:z<0,f(z)<0.5,分类y=0

更复杂的决策边界
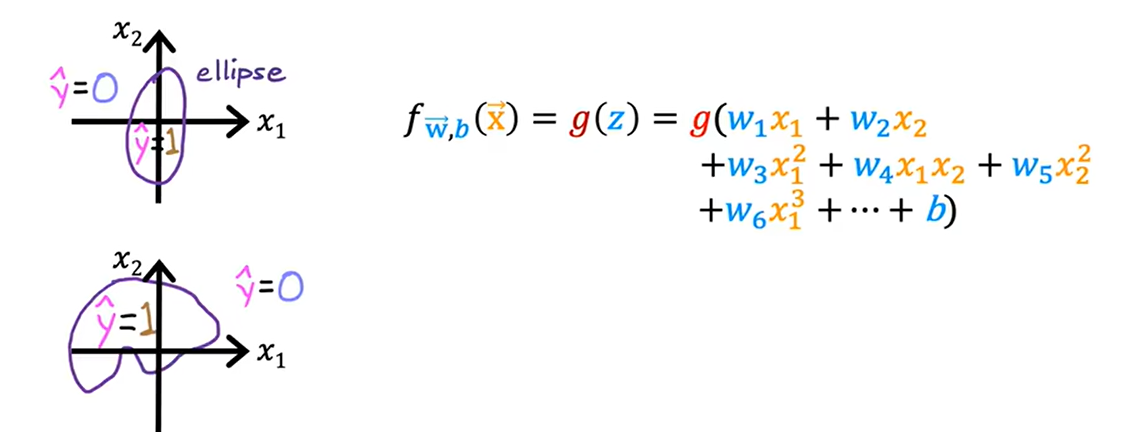
3. 逻辑回归的代价函数
代价函数提供一种衡量特定参数集对训练数据拟合程度的方法,帮助选择更好的参数
对比维度 | 损失函数(Loss Function) | 代价函数(Cost Function) |
作用对象 | 单个训练样本 | 整个训练数据集 |
数学关系 | 代价函数是损失函数的平均值 | 由损失函数累加并平均得到 |
优化目标 | 无直接优化意义 | 模型训练的目标是最小化代价函数 |
应用场景 | 理论分析、梯度计算 | 实际训练、评估模型整体性能 |
平方误差代价函数(1/2在求和符号外面时)
- 得到非凸代价函数:使用梯度下降,会有很多局部最小值

损失函数:单个训练的损失
- y^(i)真实值,f(x^(i))预测值
- 横轴:f,即标签y=1的概率预测值;纵轴:L,即损失函数
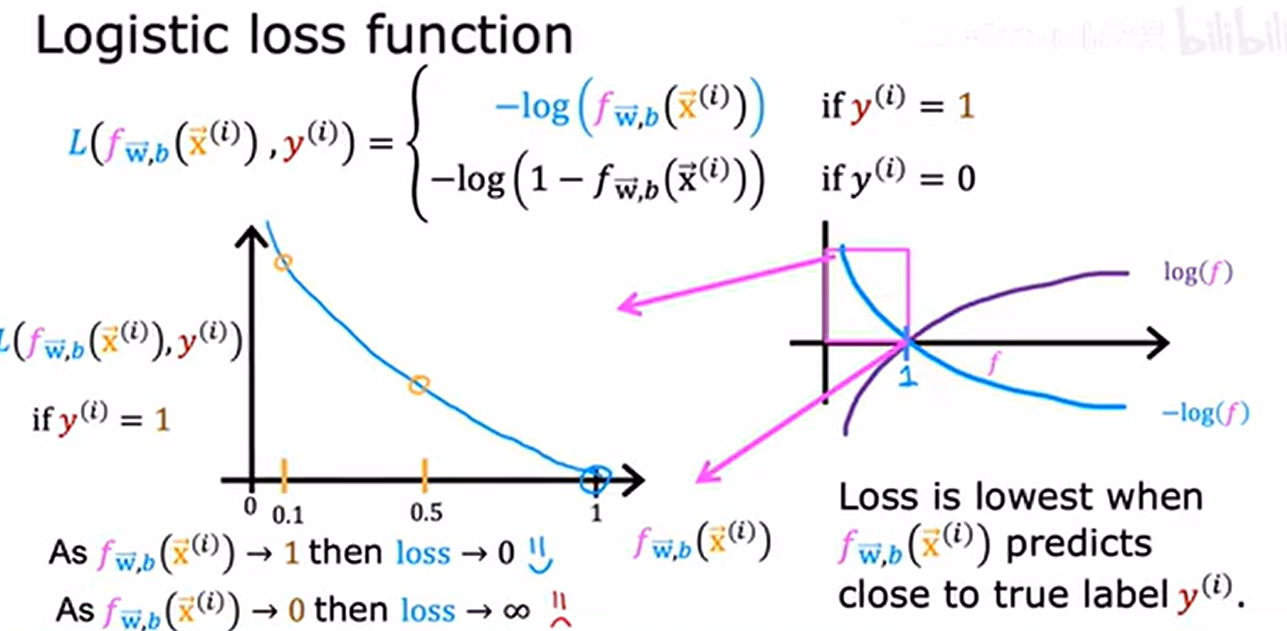
当 y^(i) = 1 时的损失函数曲线:
- 当 f(x^(i))->1(预测正确),损失 L -> 0;
- 当 f(x^(i))->0(预测错误),损失 L -> +∞
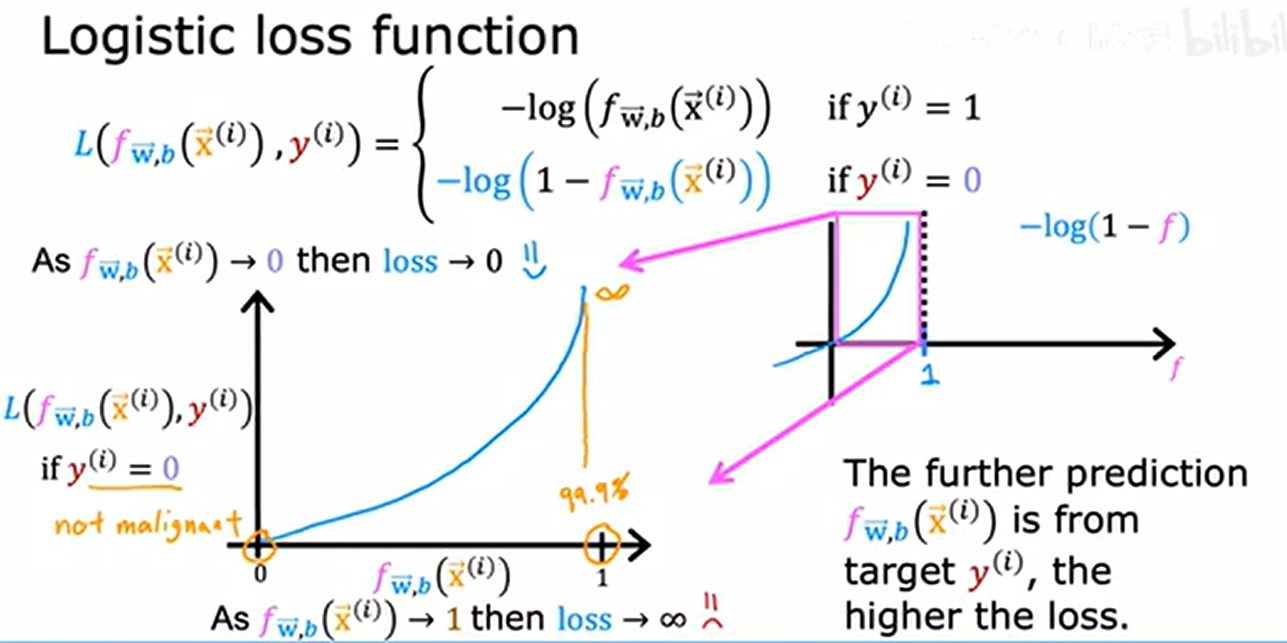
当 y^(i) = 0 时的损失函数曲线:
- 当 f(x^(i))->0(预测正确),损失 L -> 0;
- 当 f(x^(i))->1(预测错误),损失 L -> +∞
代价函数

4. 逻辑回归的简化版代价函数

5. 梯度下降的实现
如何选择w1、w2、w3、...、b的值使代价函数值尽可能小
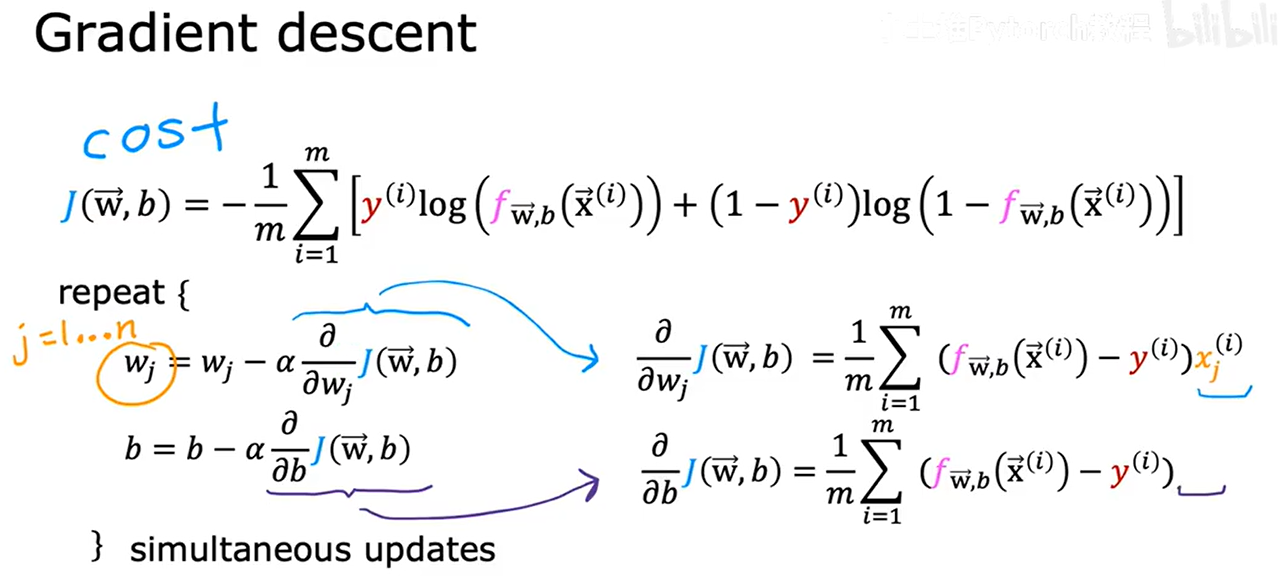
对于repeat,先计算两个式子的右侧,再同时更新到左侧
- 线性回归:预测函数为 f(x) = wx + b
- 逻辑回归:预测函数为 f(x) = 1/(1 + e^(-(wx + b)))(sigmoid 函数)
更新公式形式与线性回归的相同,但f(x)定义不同

- 监督梯度下降
- 向量化
- 特征缩放
6. 过拟合问题
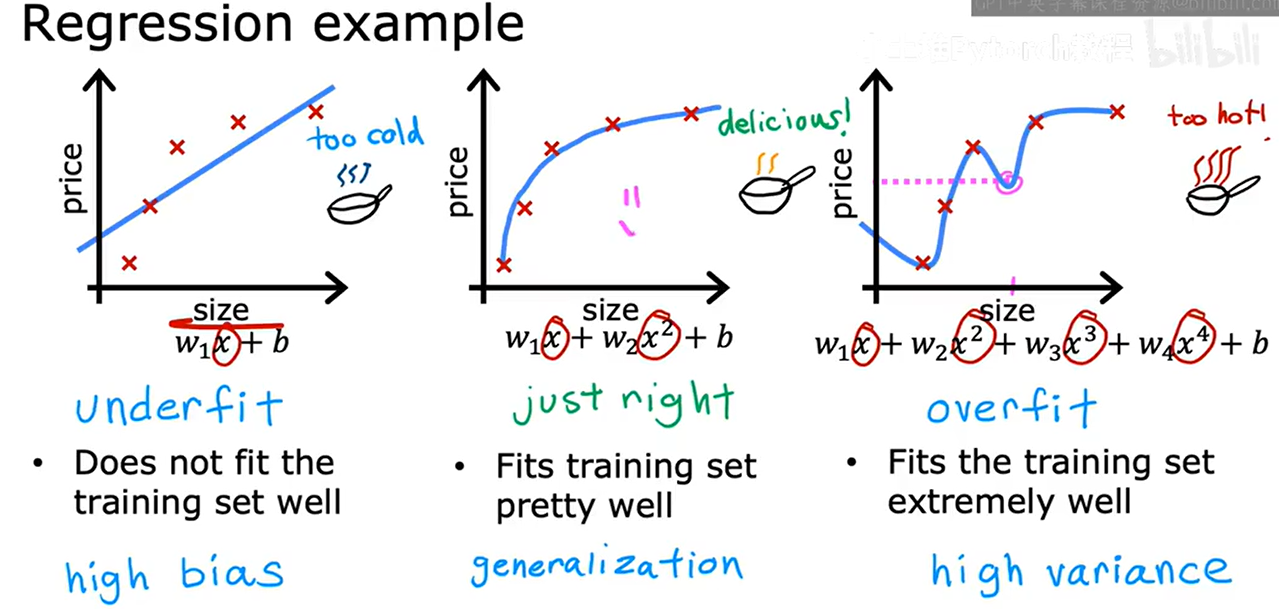
过拟合(Overfitting):模型在训练数据上表现良好,但在新的、未见过的数据上表现不佳,高方差(High Variance)
欠拟合(Underfitting):模型的复杂度较低,无法捕捉到数据中的关键特征和潜在规律,模型在训练、测试数据上的表现都很差,高偏差(High Bias)
泛化(Generalization) 是指模型在未见过的新数据上表现良好的能力。
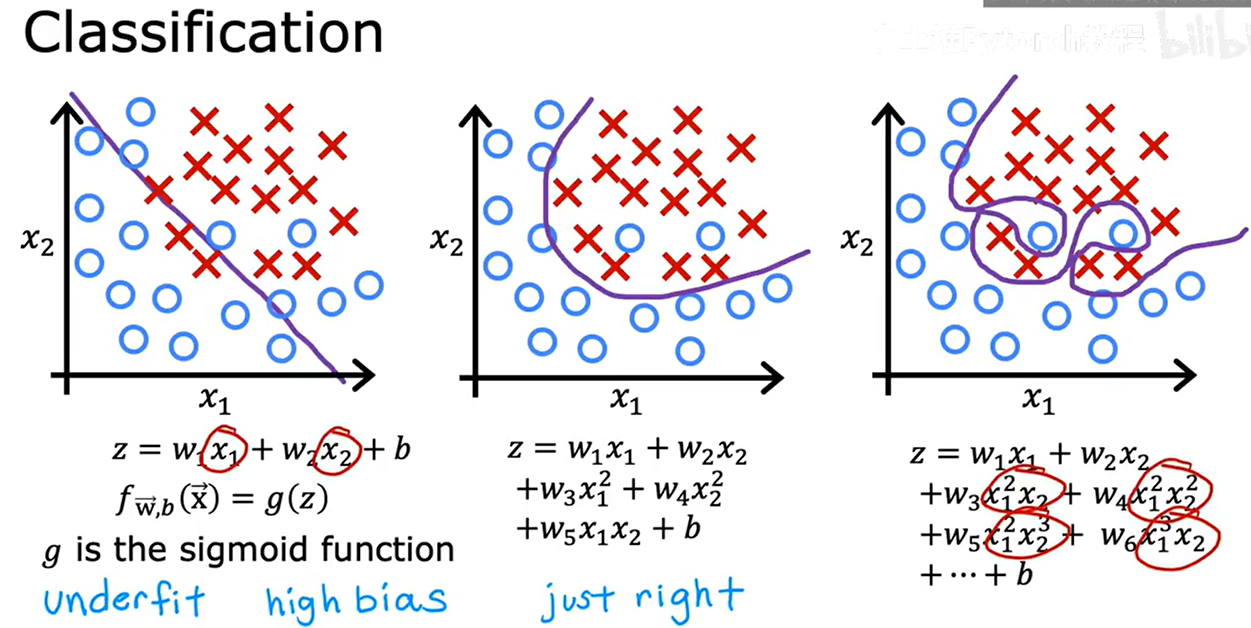
过拟合也适用于分类
7. 解决过拟合
- 获得更多数据
- 尝试选择、使用特征的子集
- 正则化减小参数大小🔺
8. 带正则化的成本函数
模型过拟合的本质是参数值过大(如高次多项式的系数),导致模型对训练数据的微小波动过度敏感。正则化通过在代价函数中引入参数惩罚项,迫使参数值 “收缩” 到较小范围,从而:
- 降低模型复杂度(避免过度复杂的决策边界);
- 增强模型对新数据的泛化能力。
正则化:对特征的参数w_j惩罚,对b不操作
- L2正则化:温和收缩参数,保留所有特征
- 所有参数 w_j 都会被 “拉向 0”,但不会严格为 0(系数值变小但非零)。
- 倾向于让参数值更平均(避免某一特征权重过大),使模型更 “平滑”。
- L1正则化:稀疏化参数,实现自动特征选择
- 部分参数 w_j 会被直接压缩至 0(“稀疏化”),相当于自动实现 “特征选择”。
- 能筛选出对目标影响最大的核心特征,剔除冗余特征。
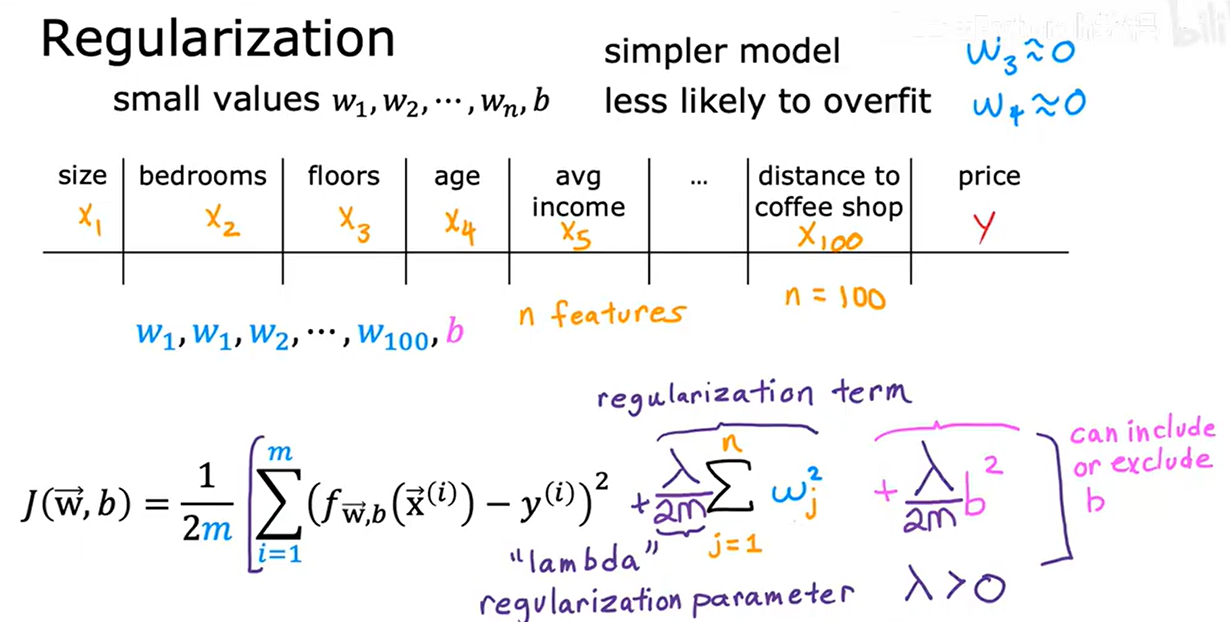
正则化参数 ⋋
- =0:无正则化,模型可能过拟合(完全拟合训练数据)。
- ⋋ 非常大:正则化权重大,所有参数 w1...wj 被压缩至 0,模型复杂度降低 f(x)~=b(可能欠拟合)。
- 选择原则:通过交叉验证(如网格搜索)找到最优 ⋋,使验证集上的模型性能(如准确率、损失值)最优。
9. 正则化线性回归
和线性回归相比,repeat部分对 b 的更新没变化,符合正则化试图缩小参数 wi ,不改变 b

正则化在每次迭代的作用:更新wj时,先✖一个略小于1的数,稍微缩小wj值,再减去

- 第一部分:w_j*(1-ɑ*⋋/m) 是正则化项,确保权重不会无限制增长。
- 第二部分:是标准的梯度下降更新项,用于最小化预测误差。
10. 正则化逻辑回归
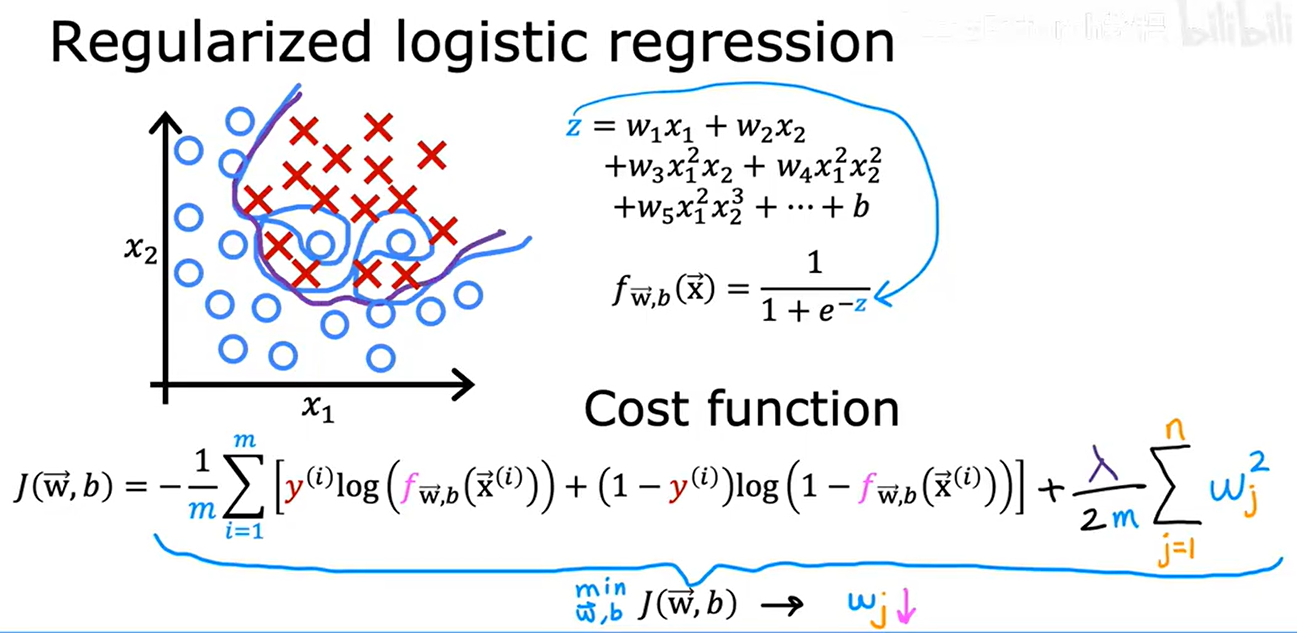
对于梯度下降迭代最小化代价函数,repeat和正则化线性回归相同,只是各自的 f(x) 函数表达式不同
