【数据结构】第七周
目录
稀疏矩阵快速转置
三元组的矩阵加法
九宫格数独游戏
数组主元素
螺旋数字矩阵
蛇形矩阵
数组循环右移K位
稀疏矩阵快速转置【问题描述】 稀疏矩阵的存储不宜用二维数组存储每个元素,那样的话会浪费很多的存储空间。所以可以使用一个一维数组存储其中的非零元素。这个一维数组的元素类型是一个三元组,由非零元素在该稀疏矩阵中的位置(行号和列号对)以及该元组的值构成。而矩阵转置就是将矩阵行和列上的元素对换。 请你实现一个快速的对稀疏矩阵进行转置的算法。 (注意:我看到部分同学提交的代码是简单转置+排序,请务必修改为快速转置算法哦。) 【输入形式】 输入的第一行是两个整数r和c(r<200, c<200, r*c <= 12500),分别表示一个包含很多0的稀疏矩阵的行数和列数。接下来有r行,每行有c个整数,用空格隔开,表示这个稀疏矩阵的各个元素。 【输出形式】 输出为读入的稀疏矩阵的转置矩阵。输出共有c行,每行有r个整数,每个整数后输出一个空格。请注意行尾输出换行。 【样例输入】 6 7 【样例输出】 0 0 -3 0 0 15 【提示】 第二组测试数据行列较大,注意空间开大一点哦。 |
#include<iostream>
using namespace std;
int text[1000][1000];
#define MAX 10001struct tr{int row;int col;int e;
};
struct ts{tr data[MAX];int m,n,len;
};void create(ts &a,int x,int y)
{a.len=0;for(int i=0;i<x;i++){for(int j=0;j<y;j++){if(text[i][j]!=0){a.data[a.len].row=i;a.data[a.len].col=j;a.data[a.len].e=text[i][j];a.len++;}}}
}
void tran(ts &a,ts &b,int x,int y)
{int tmp,Col;int t=0;int num[1000]={0};int position[1000];for(int i=0;i<a.len;i++)num[a.data[i].col]++;position[0]=0;for(int i=1;i<y;i++){position[i]=position[i-1]+num[i-1];}for(int i=0;i<a.len;i++){Col=a.data[i].col;tmp=position[Col];b.data[tmp].row=a.data[i].col;b.data[tmp].col=a.data[i].row;b.data[tmp].e=a.data[i].e;position[Col]++; }for(int i=0;i<y;i++){for(int j=0;j<x;j++){if(b.data[t].row==i&&b.data[t].col==j){cout<<b.data[t].e<<" ";t++;}else{cout<<"0 ";}}cout<<endl;}
}
int main()
{ts a,b;int i,j,x,y;cin>>x>>y;for(i=0;i<x;i++){for(j=0;j<y;j++)cin>>text[i][j];}create(a,x,y);tran(a,b,x,y);
}
三元组的矩阵加法【问题描述】 以三元组表存储的稀疏矩阵A、B非零元个数分别为m和n。试编写程序,完成A+B。 【输入形式】 第一排为分别为A、B元素的个数,以下各排分别输入对应的三元组,头m组为A中的元素,接下来为B的元素,同一个矩阵的元素按照行递增排列,第一行规定为1,同一行的元素按照列递增排列,第一列规定为1 【输出形式】 为相应的三元组,以回车分开,如果结果全部为0,则输出 -1 -1 -1 【样例输入】 2 1 1 2 3 1 3 4 1 3 3 【样例输出】 1 2 3 1 3 7 | 40 |
#include<iostream>
#include<algorithm>
using namespace std;
typedef struct{int row,col;int e;
}matrix;
bool cmp(matrix x,matrix y)
{if(x.row<y.row) return 1;else if(x.row==y.row&&x.col<y.col) return 1;else return 0;
}
int main()
{matrix a[500],b[500];int x,y,cnt=0;cin>>x>>y;for(int i=0;i<x;i++)cin>>a[i].row>>a[i].col>>a[i].e;for(int i=0;i<y;i++)cin>>b[i].row>>b[i].col>>b[i].e;int k=x;for(int i=0;i<y;i++){int flag = 1,j;for(j=0;j<x;j++){if(a[j].row==b[i].row&&a[j].col==b[i].col){flag = 0;a[j].e+=b[i].e;}}if(flag){a[k].e=b[i].e;a[k].row=b[i].row;a[k++].col=b[i].col;}}sort(a,a+k,cmp);for(int i=0;i<k;i++){if(a[i].e!=0)cnt++;}if(cnt==0){cout<<"-1 -1 -1"<<endl;return 0;}else{for(int i=0;i<k;i++){if(a[i].e!=0)cout<<a[i].row<<" "<<a[i].col<<" "<<a[i].e<<endl;}}return 0;
}
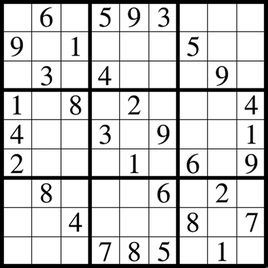
九宫格数独游戏【问题描述】
【输入形式】 【样例输出】 |
#include<iostream>
#include<cstring>
using namespace std;
int a[10][10];
bool row[10][10],col[10][10],g[10][10];void display()
{for(int i=1;i<=9;i++){for(int j=1;j<=9;j++)cout<<a[ i ][ j ]<<" ";cout<<endl;}
}
void dfs( int x ,int y)
{if(a[ x ][ y ] != 0){if( x == 9 &&y == 9)display();if( y == 9 )dfs( x + 1 , 1);elsedfs( x , y + 1 );}else{for( int i = 1 ; i <= 9 ; i++ ){if(row[x][i] && col[y][i] && g[(x-1)/3*3+(y-1)/3+1][i]){a[x][y] = i;row[x][i] = 0;col[y][i] = 0;g[(x-1)/3*3+(y-1)/3+1][i] = 0;if( x == 9 && y==9 )display();if( y==9 )dfs( x + 1, 1 );elsedfs( x , y + 1);a[x][y]=0;row[ x ][ i ]=1;col[ y ][ i ]=1;g[(x-1)/3*3+(y-1)/3+1][i]=1;}}}
}int main()
{memset(row,1,sizeof(row));memset(col,1,sizeof(col));memset(g,1,sizeof(g));for(int i=1;i<=9;i++){for(int j=1;j<=9;j++){cin>>a[i][j];if(a[i][j]>0){row[ i ][ a[i][j] ]=0;col[ j ][ a[i][j] ]=0;g[(i-1)/3*3+(j-1)/3+1][a[i][j]]=0;}}}dfs(1,1);return 0;
}
数组主元素【问题描述】这是一道2013年考研真题,已知一个整数序列A长度为N,其中若存在a,且a的个数大于N/2,则称a为A的主元素 例如:3 5 5 3 5 7 5 5,其主元素为5 又如:3 5 5 3 5 1 5 7,其中没有主元素。 假设元素保存在一个一维数组中,请设计一个尽可能高效的算法,找出主元素。若存在主元素则输出该元素否则输出 要求时间复杂度为O(N),请注意穷举法时间复杂度是O(N^2),排序再遍历查找的时间复杂度是O(N*logN+N) 【输入形式】 一个整数数组,以0作为结束输入 【输出形式】 主元素,若没有则输出-1 【样例输入】 3 5 5 3 5 7 5 5 0 【样例输出】 5 【样例说明】长度为8,共有5个‘5’ |
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{int a[100];int len=0,i=0;int sc;while(1){cin>>sc;if(sc==0) break;else a[i++]=sc;}len=i;
// for(int i=0;i<len;i++)
// cout<<a[i]<<" ";if(len==0) return 0;sort(a,a+len);
// cout<<endl;
// for(int i=0;i<len;i++)
// cout<<a[i]<<" ";int start=0,rail=0;int kk=a[len/2];for(int i=0;i<len;i++){if(a[i]==kk){start=i;break;}}for(int i=len-1;i>=0;i--){if(a[i]==kk){rail=i;break;}}
// cout<<endl<<start<<" "<<rail<<endl;int cnt=rail-start+1;if(cnt>(len/2)){cout<<kk;}else{cout<<"-1";}return 0;
}
螺旋数字矩阵
【问题描述】 编写一个程序,对任意输入的正整数n(n不大于10),产生并显示n阶螺旋式数字方阵。如n=3 要显示的方阵为
1 2 3
8 9 4
7 6 5
【输入形式】输入一个数n
【输出形式】产生n阶螺旋数字矩阵,数字以空格隔开
【样例输入】3
【样例输出】
1 2 3
8 9 4
7 6 5
【样例说明】注意输出的数字以空格隔开
#include<iostream>
#include<cstring>
using namespace std;
int dirx[4]={0,1,0,-1};
int diry[4]={1,0,-1,0};
int map[12][12];
int a[12][12];
int main()
{memset(map,sizeof(map),0);int n;cin>>n;for(int j=0;j<n+2;j++){map[0][j]=1;map[j][0]=1;map[n+1][j]=1;map[j][n+1]=1;}int num=n*n;int kk=1;a[1][1]=1;map[1][1]=1;int last=0;int i=1,j=1;while(--num){if(map[i+dirx[last]][j+diry[last]]==0){ i=i+dirx[last];j=j+diry[last];a[i][j]=++kk;map[i][j]=1;continue;}else{if(last==3) last=0;else last++;num++;continue;}}for(i=1;i<=n;i++){for(j=1;j<=n;j++)cout<<a[i][j]<<" ";cout<<endl;}} 蛇形矩阵【问题描述】蛇形矩阵是由1开始的自然数依次排列成的,按对角线方向依次递增 例如n=5时: 1 2 6 7 15 【输入形式】n 【输出形式】蛇形矩阵 【样例输入】5 【样例输出】 1 2 6 7 15 3 5 8 14 16 4 9 13 17 22 10 12 18 21 23 11 19 20 24 25 | 1.00 |
#include<bits/stdc++.h>
using namespace std;
int main()
{int a[20][20] = { 0 };int n = 0, m = 1;int i = 0, j = 0, flag = 0;cin>>n; while (m <= n * n){while (i >= 0 && (m <= n * n) && j <= n - 1){a[i][j] = m++;i--;j++;}flag++;if (flag < n)i++;else if (flag == n){i += 2;j--;}else{i += 2;j--;}while (j >= 0 && (m <= n * n) && i <= n - 1){a[i][j] = m++;i++;j--;}flag++;if (flag < n)j++;else if (flag == n){j += 2;i--;}else{i--;j += 2;}}for (int i = 0; i < n; i++){for (int j = 0; j < n; j++)printf("%d ", a[i][j]);cout<<endl;}return 0;
} 数组循环右移K位【问题描述】将一个数组中的元素循环右移K位,要求只使用一个元素大小的附加存储空间,时间复杂度为O(n)。 【样例输入】 1 2 3 4 5 6 7 8 0 2 【样例输出】 7 8 1 2 3 4 5 6 【提示】0代表输入结束 |
#include <iostream>
using namespace std;
void reverse(int start, int end, int a[], int temp)
{while (start < end){temp = a[start];a[start] = a[end];a[end] = temp;start++;end--;}
}
void move(int n, int len, int a[])
{//先把前len-step位逆置reverse(0, len - n - 1, a, a[len]);//再把后step位逆置reverse(len - n, len - 1, a, a[len]);//最后总体逆置reverse(0, len - 1, a, a[len]);
}
int main()
{ios::sync_with_stdio(false);int a[1000];int i = 0;while (1){cin >> a[i];if (a[i] == 0)break;i++;}int len = i;int step;cin >> step;step = step % len;move(step, len, a);for (int i = 0; i < len; i++)cout << a[i] << " ";
}