当前位置：首页 > news >正文

齐次线性方程组最小二乘解

news 2025/8/21 14:09:48

非齐次线性方程组：常数项不全为0的线性方程组。

$Au=b$

最小二乘解：

$u=(A^{T}A)^{-1}A^{T}b$

齐次线性方程组：常数项全为0的线性方程组。

$Au=0$

当齐次线性方程组没有严格零解时，我们需要通过最小二乘法寻找近似解，即找到非零向量 $u$ ，使得残差平方和 $\left \| Au \right \|^{2}$ 最小。

直接最小化 $\left \| Au \right \|^{2}$ 会导致零解，但零解无实际意义，因此需要添加归一化约束排除零解，最常用的约束是 $\left \| u \right \|^{2}=1$ ，即 $u^{T}u=1$ 。齐次线性方程组的解不是唯一的，可以按比例缩放，任何 $ku$ 仍是解， $\left \| u \right \|^{2}=1$ 是标准化了解的比例。

此时最小化 $\left \| Au \right \|^{2}$ 问题转化为带约束的最小二乘优化：

$\left\{\begin{matrix} min_{u}\left \| Au \right \|^{2}\\ s.t. \, \, \, u^{T}u=1 \end{matrix}\right.$

通过拉格朗日乘子法将有约束问题转为无约束问题，构造拉格朗日函数：

$L(u,\lambda )=\left \| Au \right \|^{2}-\lambda (u^{T}u-1)\\ =(Au)^{T}(Au)-\lambda (u^{T}u-1)\\ =u^{T}A^{T}Au--\lambda (u^{T}u-1)$

求极值即对 $u$ 求偏导为0（利用矩阵性质 $\frac{\partial x^{T}Ax}{\partial x}=(A^{T}+A)x$ ）:

$\frac{\partial L(u,\lambda )}{\partial u}=2A^{T}Au-2\lambda u=0\\ \\A^{T}Au=\lambda u$

结合目标函数 $\left \| Au \right \|^{2}=u^{T}A^{T}Au=\lambda u^{T}u=\lambda$ ，最小化 $\left \| Au \right \|^{2}$ 即最小化 $\lambda$ 。

所以齐次线性方程组 $Au=0$ 的最小二乘解 $u$ 是 $A^{T}A$ 的最小特征值对应的特征向量。

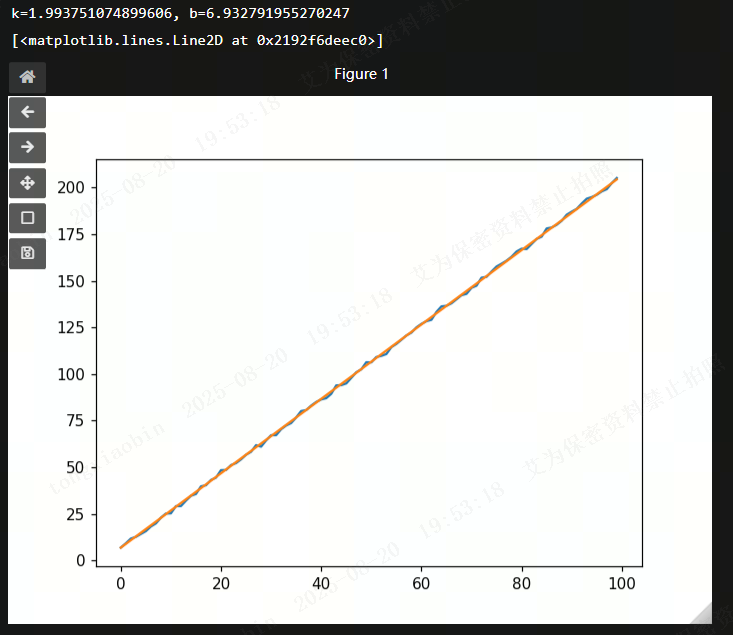
示例代码：

x = np.linspace(0, 99, 100)
y = 2 * x + 6.5 + np.random.randn(100)
plt.close('all')
plt.figure()
plt.plot(x, y)B = np.column_stack([x, y, np.ones(100)])
eigenvalues, eigenvectors = np.linalg.eig(np.dot(B.T, B))
idx = np.argmin(eigenvalues)
u = eigenvectors[:, idx]
a = u[0]
b = u[1]
c = u[2]
print("k={}, b={}".format(-a / b, -c / b))
y_pred = -a / b * x + (-c / b)
plt.plot(x, y_pred)