力扣48:旋转矩阵
力扣48:旋转矩阵
- 题目
- 思路
- 代码
题目
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
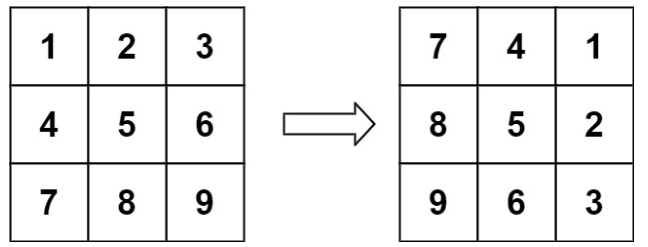
思路
这道题让我们在原地旋转矩阵不能使用另外一个矩阵辅助旋转,那么如果我们去掉这个条件这道题有什么思路呢?很简单,这里我们设行是i,列是j,从图中我们可以发现在旋转之后原本的第一行变成了最后一列,第二行变成了倒数第二列。而其中的数字顺序是没有变化的所以我们可以得出一个公式
matrix[i][j]=matrix[j][n−i−1]matrix[i][j] = matrix[j][n-i-1] matrix[i][j]=matrix[j][n−i−1]
这个公式左边是原本的位置右边是旋转后的位置,在有了这个公式后每个位置的的旋转后位置就知道了所以我们只需要创建一个新的矩阵让matrix[j][n-i-1] = matrix[i][j]即可。
但是现在这道题需要我们原地旋转矩阵所以这个方法就没法用了,那么我们重新聚焦于这个公司,为什么得到这个公式后我们没法原地旋转这个矩阵呢因为我们会给右边那个位置的值给覆盖掉,想要避免这个情况我们可以定义一个temp来存储它的值,所以我们现在只要知道右边那个位置旋转之后的位置在哪就可以了,一样还是这个公式只不过我们是把它的行列当作一个整体来看就可以了
matrix[j][n−i−1]=matrix[n−i−1][n−j−1]matrix[j][n-i-1] = matrix[n-i-1][n-j-1] matrix[j][n−i−1]=matrix[n−i−1][n−j−1]
那么又回到了原来的问题,覆盖的位置的值还是用temp来保存那么它旋转后的位置在哪呢?一样用公式
matrix[n−i−1][n−j−i]=mtrix[n−j−1][i]matrix[n-i-1][n-j-i] = mtrix[n-j-1][i] matrix[n−i−1][n−j−i]=mtrix[n−j−1][i]
继续还是一样的思路,再用公式
matrix[n−j−i][i]=matrix[i][j]matrix[n-j-i][i] = matrix[i][j] matrix[n−j−i][i]=matrix[i][j]
我们发现转了一圈又回来了,所以这就是一个圈,四个位置形成一个圈。我们可以用temp存储matrix[i][j]的值然后一个一个的赋值。
那么既然是四个形成一圈我们是不是可以把整个矩阵分成四部分这样我们只需要遍历其中的一部分就可以完成整个旋转的操作了,所以问题又出现了这是一个n*n的矩阵我们要怎么分成四部分呢?分两种情况,n为偶数和n为奇数。

当n为偶数时分成四部分后一部分的数量就是n^2/4即(n/2)*(n/2)。
当n为奇数时我们要注意中间的位置是不会动的所以分成四部分后一部分的数量就是(n^2-1)/4,利用平方差公式和一些因式分解就可以得到最后的结果是(n-1)/2*(n+1)/2。
这两个情况一结合我们就可以发现我们需要遍历的行就是n/2,需要遍历的列是(n+1)/2。
代码
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n = matrix.size();for (int i = 0; i < n / 2; i++) { // 行for (int j = 0; j < (n + 1) / 2; j++) { // 列int temp = matrix[i][j];matrix[i][j] = matrix[n - j - 1][i];matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];matrix[j][n - i - 1] = temp;}}}
};
