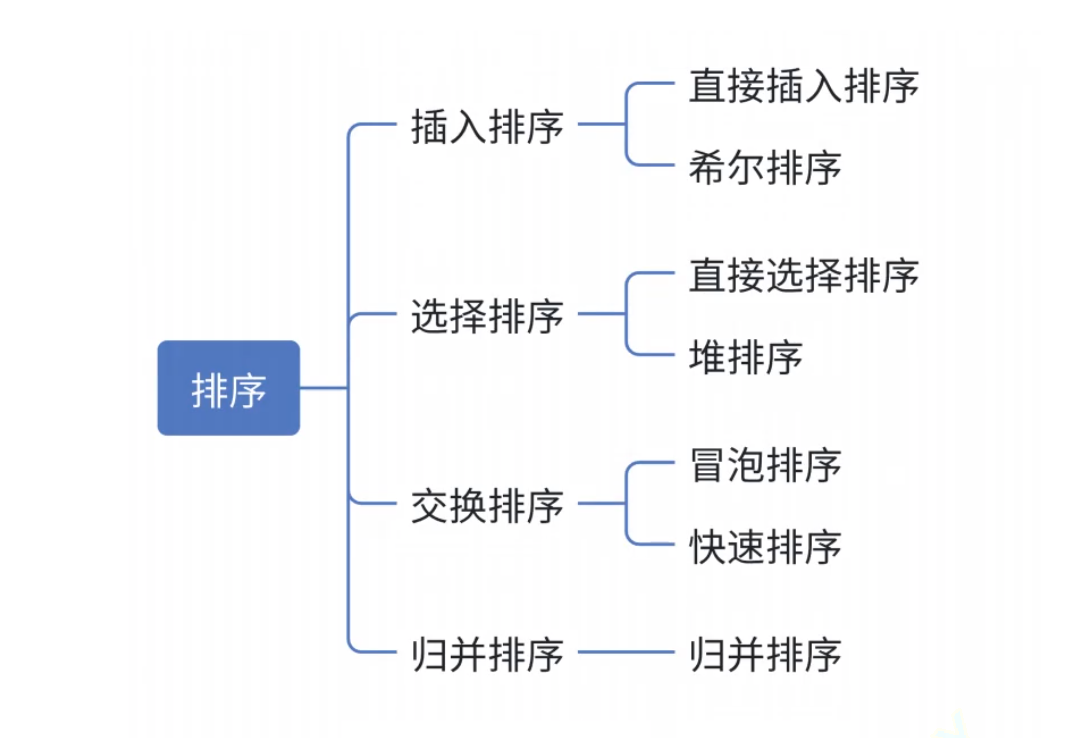
数据结构之排序大全(1)
排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或者某些关键字的大小,递增或递减地排序起来的操作。
今天我们的主角是插入排序。
插入排序
直接插入排序
基本思想
直接插入排序是一种简单的插入排序法,其基本思想是:把待排序的记录按照其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插完为止,得到一个新的有序序列。
举个例子,假设我们现在在玩扑克牌,我开始有0张牌,当摸到一张牌以后这张牌在我手里就相当于是有序的,现在再摸剩余的牌,我再将它按照一定的排序规则插入到原来的牌中,我手中的拍就一直是有序的。在摸牌过程中,我们每次将新拿到的牌按照顺序插入到已经在我手里排过序的牌中,摸完牌后,我手里的所有牌就都是有序的了。
直接插入排序的图示解析过程:

根据解析来写代码:
//直接插入排序
void InsertSort(int* arr, int n)
{for (int i = 0; i < n-1; i++){int end = i;//end表示已经排好序列的最后一个元素的下标,初始已经排好的序列中只有一个元素//这个元素就是数组中的第一个元素,下标是0//循环将end的下一个元素放到已经排好序的序列中int tmp = arr[end + 1];while (end >= 0){//找到tmp应该放在的位置if (arr[end] > tmp){arr[end + 1] = arr[end];end--;}else{break;}}arr[end + 1]=tmp ;}
}时间复杂度分析:当我们要将数组排成升序的时候,如果原来数组的序列是完全降序排列的,那么时间复杂度达到最坏情况,因为此时内层循环要循环的此时达到最大,此时时间复杂度的计算:1+2+3+……+(n-1)=n*(n-1)/2,所以时间复杂度是O(n^2)。当数组接近有序时或者满足小的数据在前,大的数据在后时,时间复杂度情况最好,大约是O(N)。
希尔排序
前面我们已经说过了,直接插入排序最坏的时间复杂度是O(N^2),但是这种情况还是比较少见的,只有当数组顺序是完全倒序的时候才会出现。但如果我们想要时间复杂度接近O(N),就需要数组满足大的数据在后,小的数据在前,我们能否根据这个对直接插入排序进行优化?
当然可以,这就是我们接下来要学习的希尔排序了。
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数(通常是gap = n/3+1),把待排序文件所有记录分成各组,所有的距离相等的记录分在同一组内,并对每一组内的记录进行排序,然后gap=gap/3+1得到下一个整数,再将数组分成各组,进行插入排序,当gap=1时,就相当于直接插入排序。
它是在直接插入排序算法的基础上进行改进而来的,综合来说它的效率肯定是要高于直接插入排序算法的。
我们来画图演示一下:
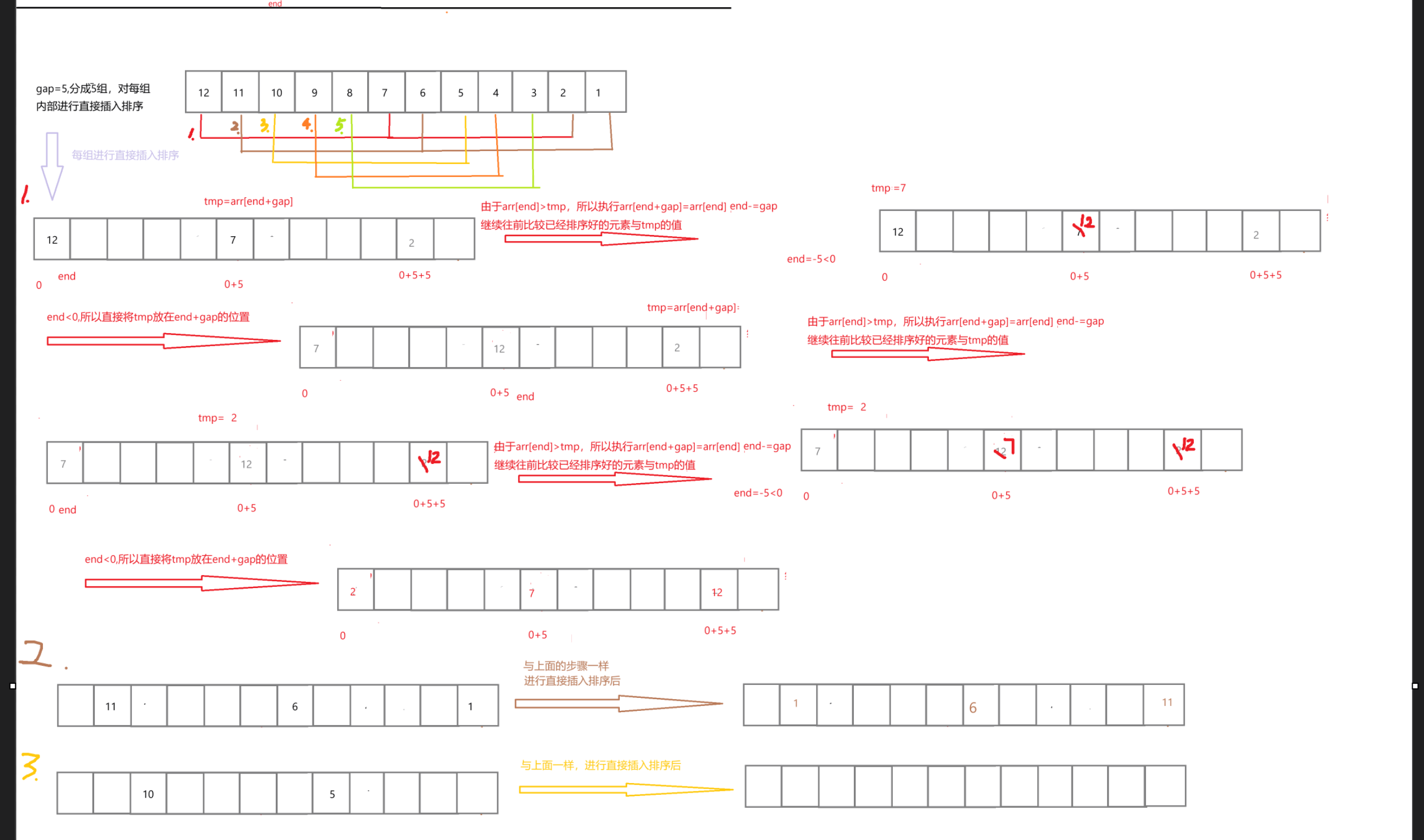
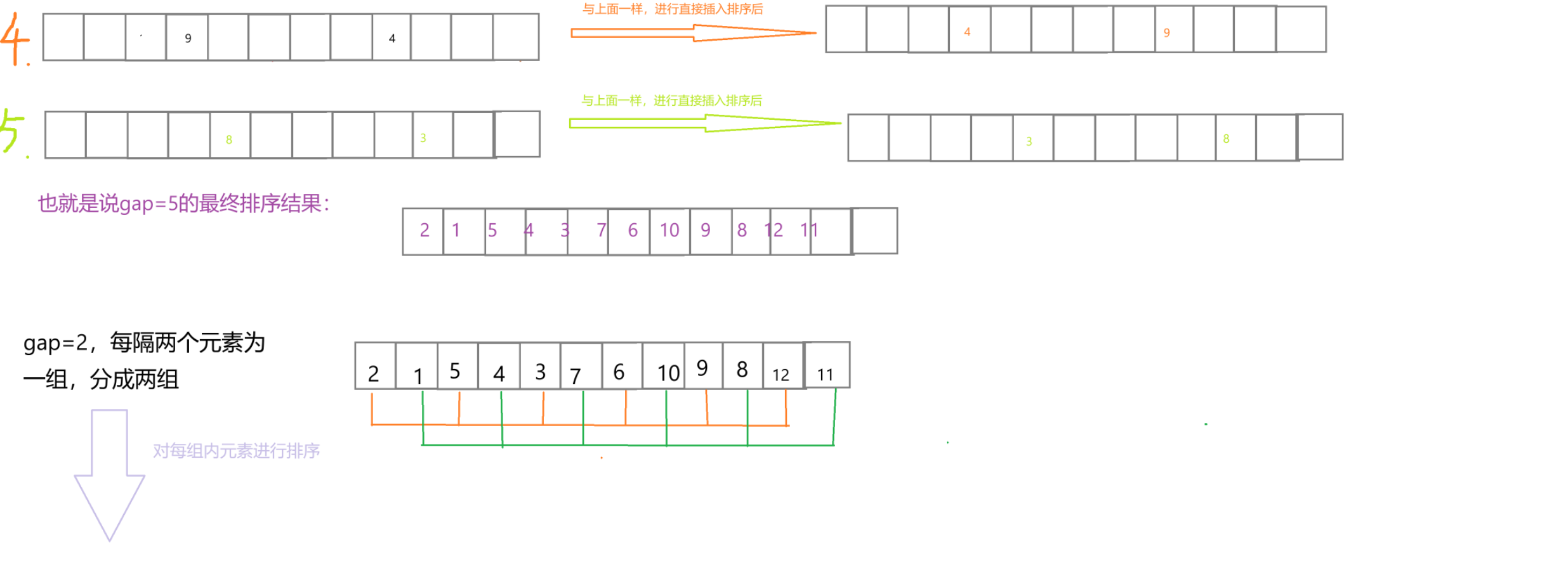
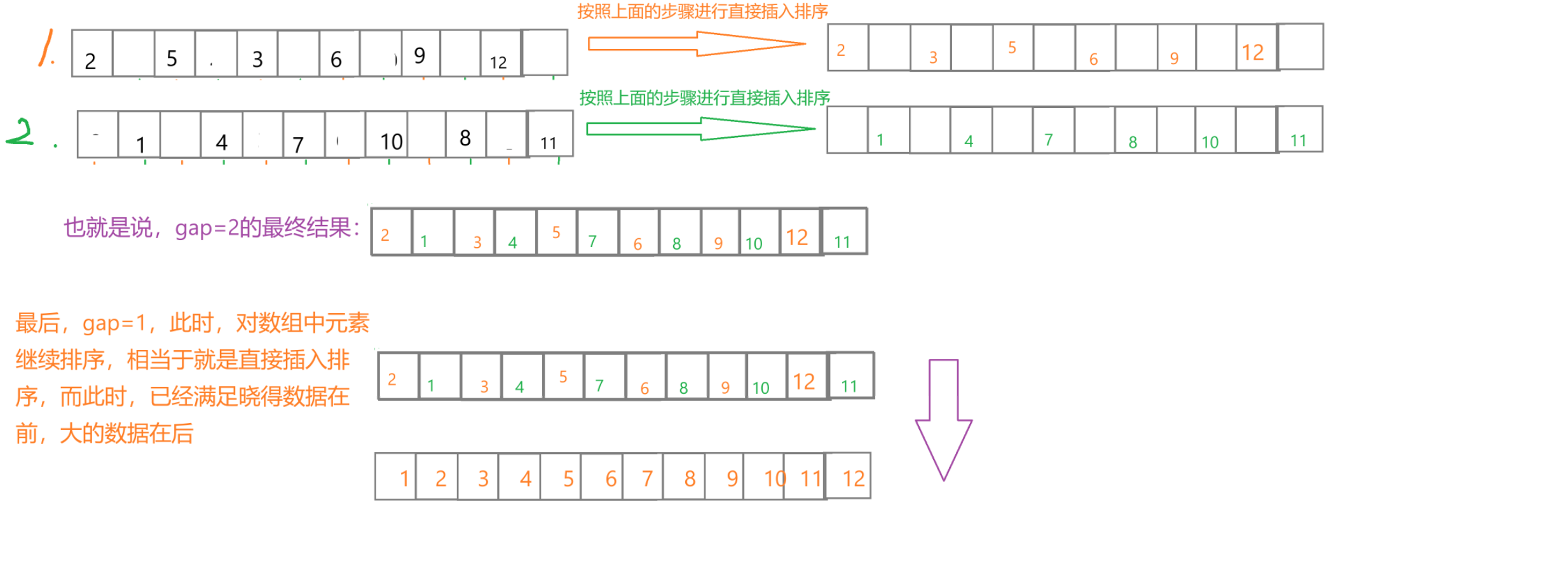
我们可以看到,希尔排序就是直接插入排序的优化,我们设定了一个间隔gap,这个gap最后一定会变成1,。我们先将数组分成gap组,然后对每组内的元素分别进行直接插入排序,在gap=1之前进行的排序都是预排序,在gap=1时,排序就是刚才讲的的直接插入排序,但此时数组满足大的数据在后,小的数据在前,所以时间复杂度较低,从而达到了优化,我们据此来写以下代码:
//希尔排序——显示分组版
void ShellSort(int* arr, int n)
{int gap = n;//初始化间隔while (gap > 1){gap = gap / 3 + 1;//Knuth 提出的经典增量序列,能让希尔排序性能更好//已经选定了gap,开始对组内元素进行直接插入排序for (int i = 0; i < gap; i++)//一共有gap组{//直接插入排序算法的改编,来简单解释一下://当i=0的时候,j=gap,end=j-gap=0,此时end指向的是第一组的第一个元素,// j指向的是第一组的第二个元素,也表示第一组内第一个要插入的元素//当i=1的时候,j=1+gap,end=1,此时end执行那个的事第二组的第一个元素,//j指向的是第二组的第二个元素,也表示第二组内要插入的第一个元素//……//总的来说,i就是每小组内的第一个元素的下标,相当于直接插入排序中end的初始值// j指向的就是每小组内第一个待插入的元素的下标,j位置上的元素值相当于直接插入排序中tmpfor (int j = i +gap; j < n; j += gap){int end = j - gap;int tmp = arr[j];while (end >= i)//i表示的是每组的组头元素{if (arr[end] > tmp){arr[end + gap] = arr[end];end -= gap;}else {break;}}//找到了tmp应该在的位置arr[end + gap] = tmp;}}}
}大家需要仔细看一下算法和注释内容。
但是,我们会发现这个算法中我们写了4个嵌套循环,看着就有点难办,那有没有什么方法改进一下呢?
有的兄弟们,我们先来看代码,再来画图解释:
//希尔排序——优化版
void ShellSort_1(int* arr, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = arr[end + gap];while (end >= 0){if (arr[end] > tmp){arr[end + gap] = arr[end];end -= gap;}else{break;}}arr[end + gap] = tmp;}}
}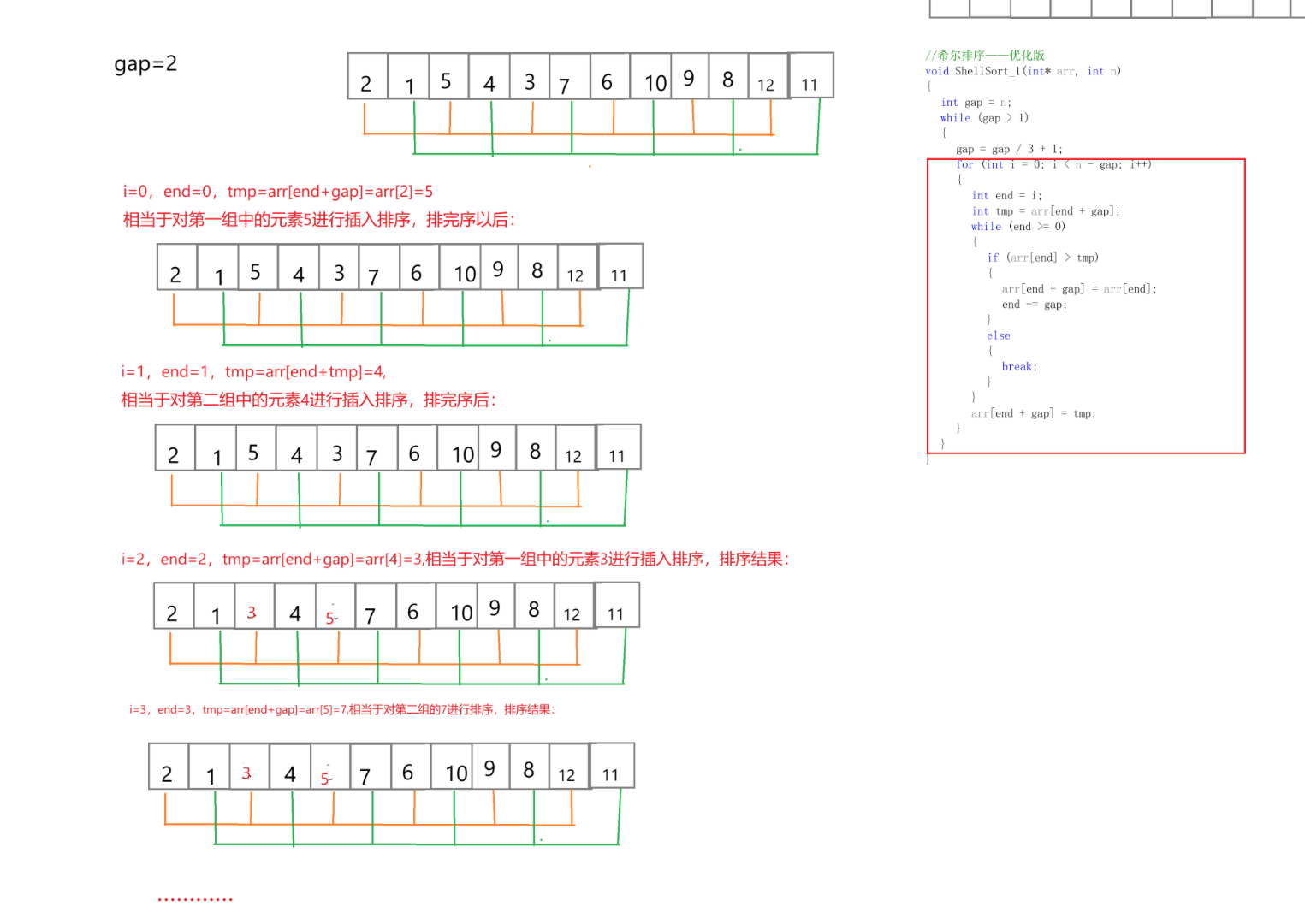
也就是说,之前我们写希尔排序是先对一组中所有元素排完序以后再对下一组进行排列,但是我们修改代码以后,就变成了:调整完A组的元素在A组的顺序后,就不再接着调整A组中剩余的元素,而是先调整B组中的元素,以此类推,最终调整的效果与修改代码前还是一样的。
简单解释为什么gap的变化是:gap=gap/3+1?
gap = gap / 3 + 1 这个简洁的公式实现了两个目标:
高效递减:通过除以 3 让间隔快速缩小,减少了排序的趟数。
绝对收敛:通过加 1 保证了序列的最后一个值一定是 1,使得算法最终能完成一次完整的插入排序,从而保证结果100%正确。
这是一种在效率(更少的排序趟数)和正确性(最终Gap=1)之间取得的完美平衡,并且计算非常简单,因此被广泛采用。
希尔排序的时间复杂度

所以,我们一般认为希尔排序的时间复杂度是O(n^(1.3)).
结语:今天我们主要是学习了插入排序的两种算法,作为直接插入排序的进阶,希尔排序是比较高效的,但小编认为它理解起来还是有一点点难度的,还是那句话,大家一定要自己好好敲代码呀。喜欢小编文章的小伙伴们可以关注一下小编哦,小编会及时更新新的文章的!
