换根DP（P3478 [POI 2008] STA-StationP3574 [POI 2014] FAR-FarmCraft）

换根DP

换根DP（又称二次扫描法）是一种树形动态规划技术，用于解决需要以每个节点为根重新计算子树信息的问题。核心思想是通过一次DFS预处理子树信息，再通过第二次DFS利用父节点信息推导其他根节点的结果，避免对每个根节点单独计算，将时间复杂度优化至O(n)。

核心思想

1. 第一次DFS（后序遍历）：以任意节点（通常为根节点）为起点，计算子树内的局部信息（如子树大小、子树路径和等）。
2. 第二次DFS（前序遍历）：从根节点出发，利用父节点的全局信息推导子节点的全局信息。通过“换根”操作，将父节点的结果转移到子节点。

典型问题：求树中每个节点的最长路径

问题描述：给定一棵无向树，求以每个节点为根时的最长路径（直径）。

C++实现

#include <vector>
#include <algorithm>
using namespace std;const int N = 1e5 + 10;
vector<int> g[N];  // 邻接表存树
int down1[N], down2[N];  // 记录子树最长路径和次长路径
int up[N];              // 记录父节点传递的全局信息
int res[N];             // 存储每个节点的最终结果// 第一次DFS：预处理子树信息（后序遍历）
void dfs1(int u, int fa) {for (int v : g[u]) {if (v == fa) continue;dfs1(v, u);int len = down1[v] + 1;  // 假设边权为1if (len > down1[u]) {down2[u] = down1[u];down1[u] = len;} else if (len > down2[u]) {down2[u] = len;}}
}// 第二次DFS：换根计算全局信息（前序遍历）
void dfs2(int u, int fa) {res[u] = max(down1[u], up[u]);  // 合并子树和父节点信息for (int v : g[u]) {if (v == fa) continue;// 核心换根逻辑：判断v是否在u的最长路径上if (down1[u] == down1[v] + 1) {up[v] = max(up[u], down2[u]) + 1;} else {up[v] = max(up[u], down1[u]) + 1;}dfs2(v, u);}
}int main() {int n; scanf("%d", &n);for (int i = 1; i < n; i++) {int a, b; scanf("%d%d", &a, &b);g[a].push_back(b);g[b].push_back(a);}dfs1(1, -1);  // 假设1为初始根节点dfs2(1, -1);for (int i = 1; i <= n; i++) printf("%d\n", res[i]);return 0;
}

关键点

1. 状态定义：down1[u]和down2[u]分别记录以u为根的子树的最长和次长路径，up[u]记录父节点传递的路径长度。
2. 换根转移：在第二次DFS中，根据父节点信息更新子节点的up值，需判断子节点是否在父节点的最长路径上。
3. 复杂度：两次DFS均为O(n)，适合大规模树结构问题。

应用场景

• 树的直径（任意根最长路径）
• 树中每个节点的子树权值和
• 网络拓扑中的最优中心节点选择

P3478 [POI 2008] STA-Station

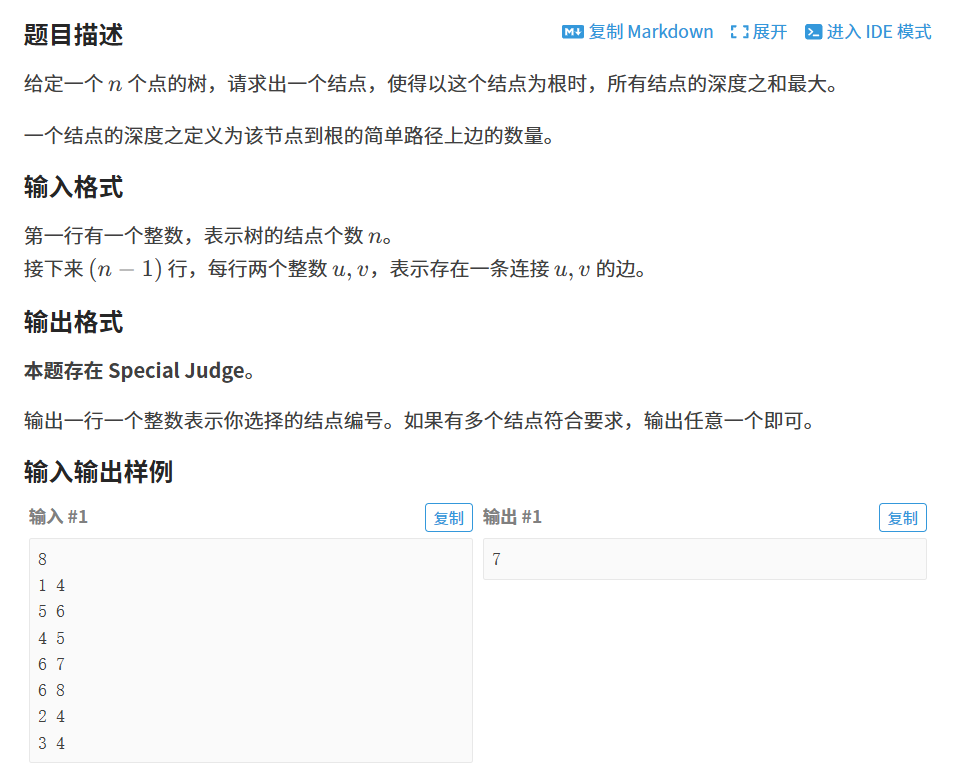
思路：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long 
using namespace std;
struct{int to, next;
}a[2000006];
int h[1000006], head[1000006];//head深度
int hh[1000006];//hh包括自身的节点数
ll dp[1000006];
int n;
ll max_head, max_i;int qq = 0;
void chua(int l, int r) {a[++qq].to = r;a[qq].next = h[l];h[l] = qq;
}
int  chuhead(int i, int fa) {    int q = h[i];if (q == 0) {return 0;}head[i] = head[fa] + 1;while (q != 0) {if (a[q].to != fa) {hh[i]+=chuhead(a[q].to, i);}q = a[q].next;}hh[i] += 1;return hh[i];
}
void dfs(int i,int fa) {int q = h[i];if (q == 0) {return ;}if (i != 1) {dp[i] = dp[fa] + n - 2LL * hh[i];}while (q != 0) {if (a[q].to != fa) {dfs(a[q].to, i);}q = a[q].next;}
}
int main(){ios::sync_with_stdio(false);        // 禁用同步cin.tie(nullptr);                   // 解除cin与cout绑定cin >> n;int l, r;for (int i = 0; i < n-1; i++) {cin >> l >> r;chua(l, r), chua(r, l);}chuhead(1, 0);for (int i = 1; i <= n; i++) {dp[1] += head[i];}dfs(1, 0);max_head = dp[1], max_i = 1;for (int i = 1; i <= n; i++) {if (dp[i] > max_head) {max_head = dp[i];max_i = i;}}cout << max_i << endl;return 0;
}

P3574 [POI 2014] FAR-FarmCraft

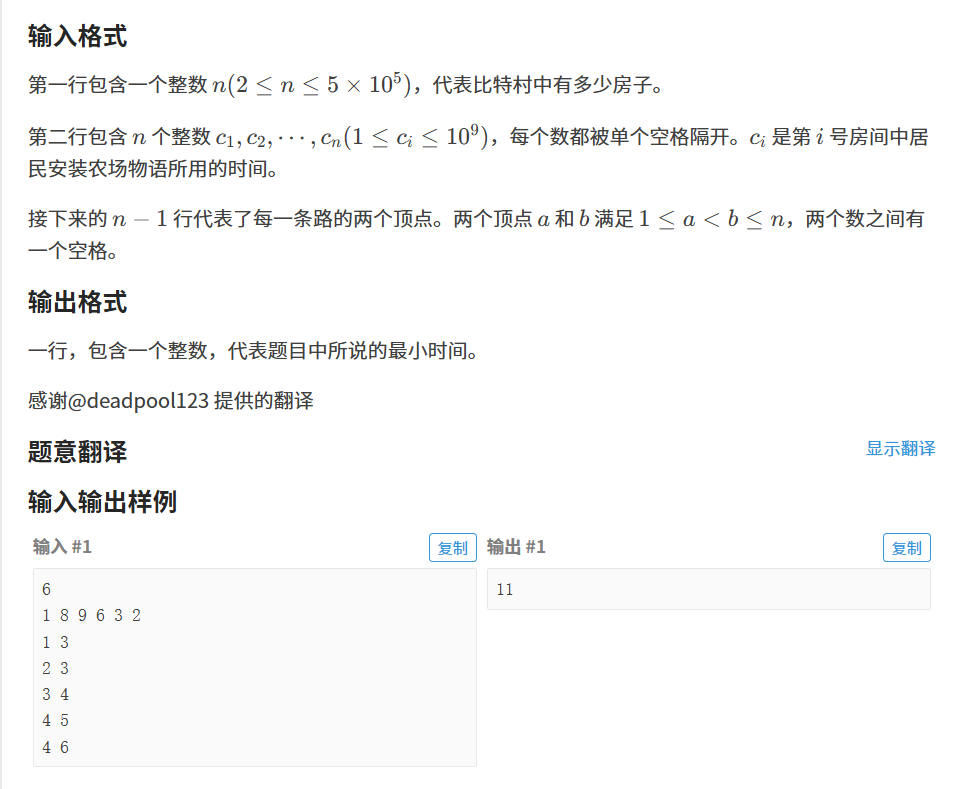
思路：

核心思路

代码分为两个主要部分：chu函数和dfs函数，分别完成子树大小计算和后序遍历动态规划。

子树大小计算（chu函数）

• 递归计算每个节点的子树大小（包含自身），结果存储在head数组中。
• 对于叶子节点（a[i].size() == 1且非根节点），直接返回1。
• 非叶子节点则累加所有子节点的子树大小，公式为： [ head[i] = \sum_{j \in children(i)} (head[j] + 1) ]

动态规划（dfs函数）

• 后序遍历处理每个节点，动态更新c[i]的值。
• 对每个节点的子节点，根据优先级（c[a[i][z]] - 2*(head[a[i][z]]+1)）排序，确保优先处理关键子节点。
• 更新逻辑分为两部分：
  1. 根节点（i == 1）直接赋值为2*(n-1)（可能表示全树的边权总和）。
  2. 非根节点累加当前路径权重w，并通过比较子节点的贡献值动态调整c[i]： [ c[i] = \max\left(ah[z].first + 2*q, c[i]\right) ] 其中q为剩余未处理的子树总大小。

关键变量

• head[i]：节点i的子树大小（不含自身）。
• c[i]：动态规划的目标值，最终输出c[1]。
• a：邻接表存储树结构。
• ah：临时数组，存储子节点的优先级和编号。

复杂度分析

• 时间复杂度：O(n \log n)，排序操作占主导。
• 空间复杂度：O(n)，递归栈和数组存储均为线性。

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long 
using namespace std;
vector<vector<int>>a(500005);
int n;
int head[500005], c[500005];//head->他下方包含多少边
bool b[500005];//判断是否被使用过;
typedef pair<int, int> pii;
int chu(int i,int i0) {if (a[i].size() == 1&&i0!=0) {head[i] = 0;return head[i]+1;}for (int j = 0; j < a[i].size(); j++) {if (a[i][j] != i0) {head[i] += chu(a[i][j], i);}}return head[i] + 1;
}
void dfs(int i, int w, int i0) {for (int j = 0; j < a[i].size(); j++) {if (a[i][j] != i0) {dfs(a[i][j], w + 1, i);}}int q = head[i];vector<pii>ah(a[i].size());int o = 0;for (int z = 0; z < a[i].size(); z++) {if (a[i][z] != i0) {ah[o].first = c[a[i][z]] - 2 * (head[a[i][z]] + 1);ah[o].second = a[i][z];o++;}}sort(ah.begin(), ah.begin()+o);if(i!=1){c[i] += w;}else {c[i] += 2 * (n - 1);}for (int z = 0; z < o; z++) {c[i] = max(ah[z].first + 2 * q,c[i]);q -= head[ah[z].second]+1;}
}
int main(){ios::sync_with_stdio(false);        // 禁用同步cin.tie(nullptr);                   // 解除cin与cout绑定cin >> n;for (int i = 1; i <= n; i++) {cin >> c[i];}int l, r;for (int i = 0; i < n - 1; i++) {cin >> l >> r;a[l].push_back(r);a[r].push_back(l);}chu(1, 0);dfs(1, 0, 0);cout << c[1] << endl;return 0;
}