有序二叉树的删除
有序二叉树的删除需要考虑多种情况,其核心在于在删除节点之后,依然保持有序二叉树的性质,即左子树所有节点值 < 当前节点值 < 右子树所有节点值。
下面,我们用如下这棵树作为例子,分析关于有序二叉树所要删除的目标节点的几种可能情况。
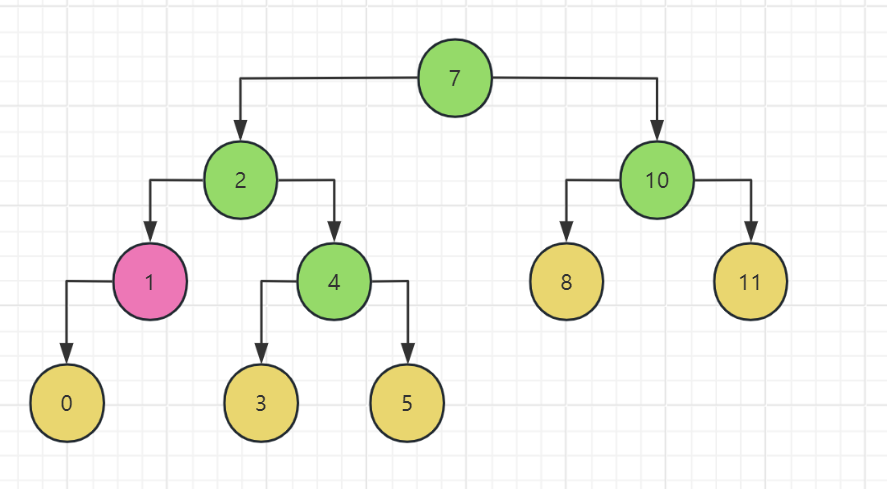
我们大致可以将其分类为以下三种情况:
- 目标节点为叶子节点(黄色节点)
- 目标节点只有一颗子树(粉色节点)
- 目标节点有两棵子树(绿色节点)
当目标节点分别是这三种情况时,有序二叉树的删除该如何实现?
一、删除叶子结点
(一)逻辑方法
1、找到要删除的目标节点target;
2、判断目标节点是否有父节点parent;
3、如果没有父节点,即整棵树就只有一个节点,则root=null;
4、如果有父节点,判断父节点和目标节点的关系
(1)目标节点是父节点的左孩子,则parent.left=null
(2)目标节点是父节点的右孩子,则parent.right=null
(二)示例
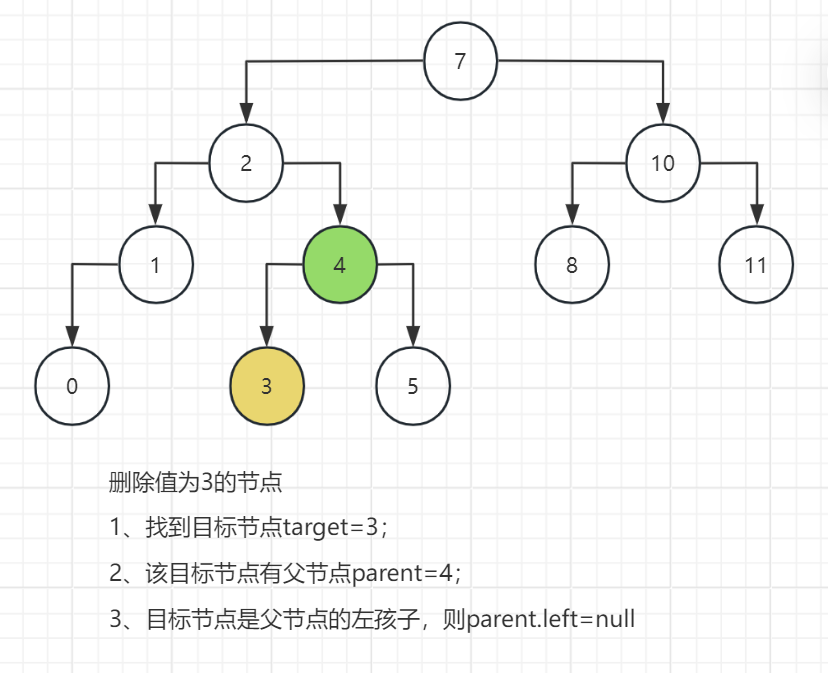
(三)关键部分的代码实现
//如果没有父节点
if(parent==null) {root=null;return;
}
//如果有父节点
//判断目标节点是父节点的左孩子还是右孩子
if(parent.left!=null&&parent.left.value==num) {//目标节点是父节点的左孩子parent.left = null;
}else {//目标节点是父节点的右孩子parent.right=null;
}二、删除只有一颗子树的节点
(一)逻辑方法
1、找到目标节点target;
2、判断目标节点是否有父节点parent;
3、如果没有父节点,即目标节点是根节点,且只有一颗子树
(1)目标节点只有一颗左子树,则root=target.left;
(2)目标节点只有一颗右子树,则root=target.right;
4、如果目标节点有父节点,判断目标节点和父节点的关系
(1)目标节点是父节点的左孩子,且目标节点有一颗左子树,则parent.left=target.left;
(2)目标节点是父节点的左孩子,且目标节点有一颗右子树,则parent.left=target.right;
(3)目标节点是父节点的右孩子,且目标节点有一颗左子树,则parent.right=target.left;
(4)目标节点是父节点的右孩子,且目标节点有一颗右子树,则parent.right=target.right;
(二)示例
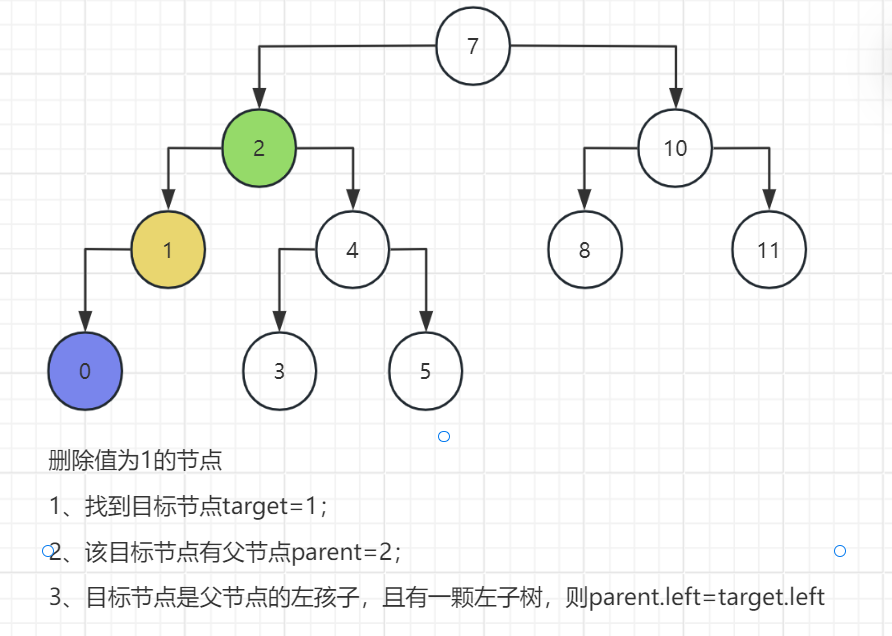
(三)关键部分的代码实现
//目标节点右子树的最小值
Node index = target.right;
while (index.left!=null) {index=index.left;
}
//最小值
int min = index.value;//先删除
delete(min);
//替换
target.value = min;三、删除两颗子树的节点
(一)逻辑方法
1、找到目标节点target;
2、找到目标节点左子树的最大值或右子树的最小值,替换目标节点的值;
3、删除目标节点左子树的最大值或右子树的最小值;
(二)示例
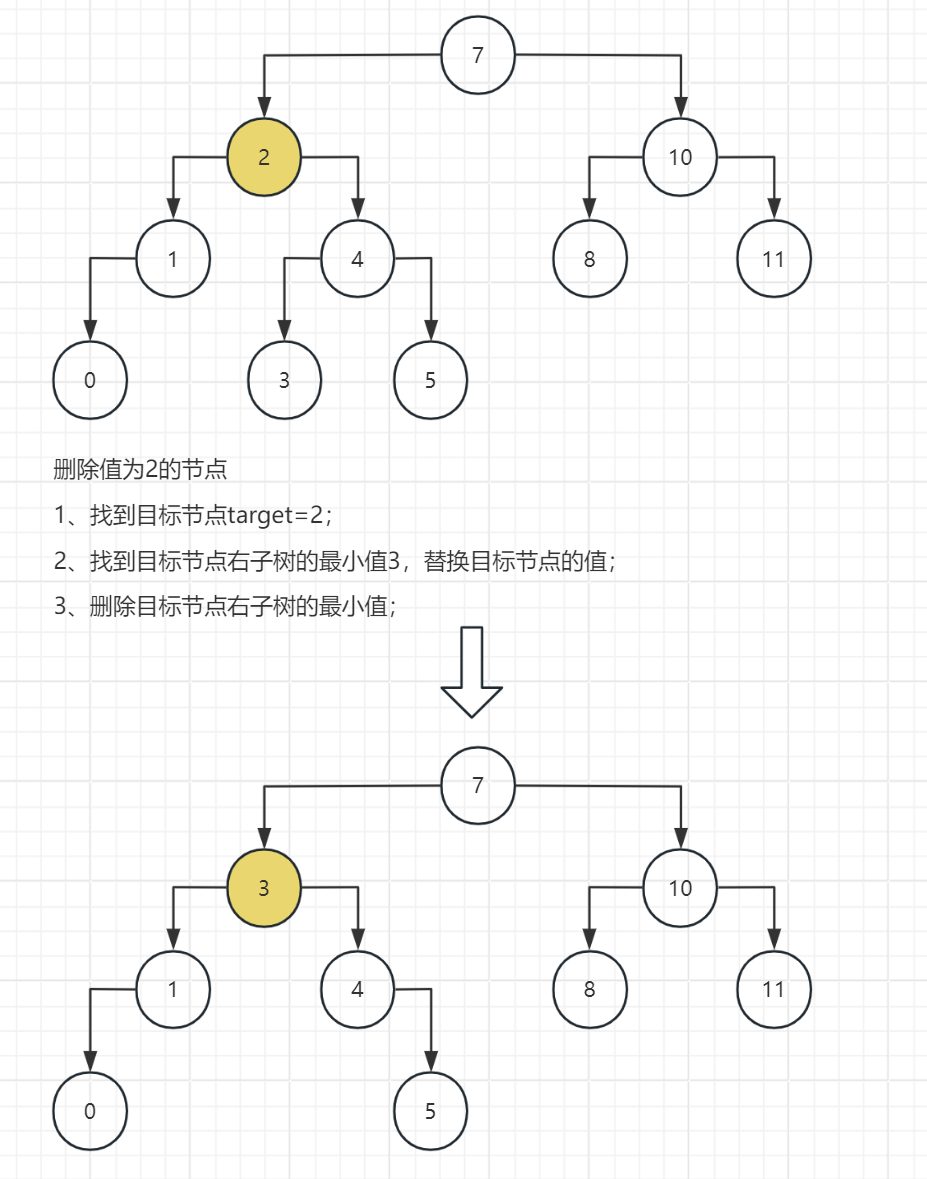
(三)关键部分的代码实现
//没有父节点
if(parent==null) {//判断目标节点有左子树还是右子树if(target.left!=null) {//目标节点有左子树root = target.left;}else {//目标节点有右子树root = target.right;}return;
}
//有父节点 判断目标节点和父节点的关系
//判断目标节点是父节点的左孩子还是右孩子
if(parent.left!=null&&parent.left.value==num) {//目标节点是父节点的左孩子//判断目标节点有左子树还是右子树if(target.left!=null) {//目标节点有左子树parent.left = target.left;}else {//目标节点有右子树parent.left = target.right;}
}else {//目标节点是父节点的右孩子//判断目标节点有左子树还是右子树if(target.left!=null) {//目标节点有左子树parent.right = target.left;}else {//目标节点有右子树parent.right = target.left;}
}