当前位置：首页 > news >正文

[优选算法专题二——找到字符串中所有字母异位词]

news 2025/8/20 12:39:35

题目链接

438.LeetCode找到字符串中所有字母异位词

题目描述

题目解析

两种方法：定长滑窗/不定长滑窗

方法一：定长滑窗

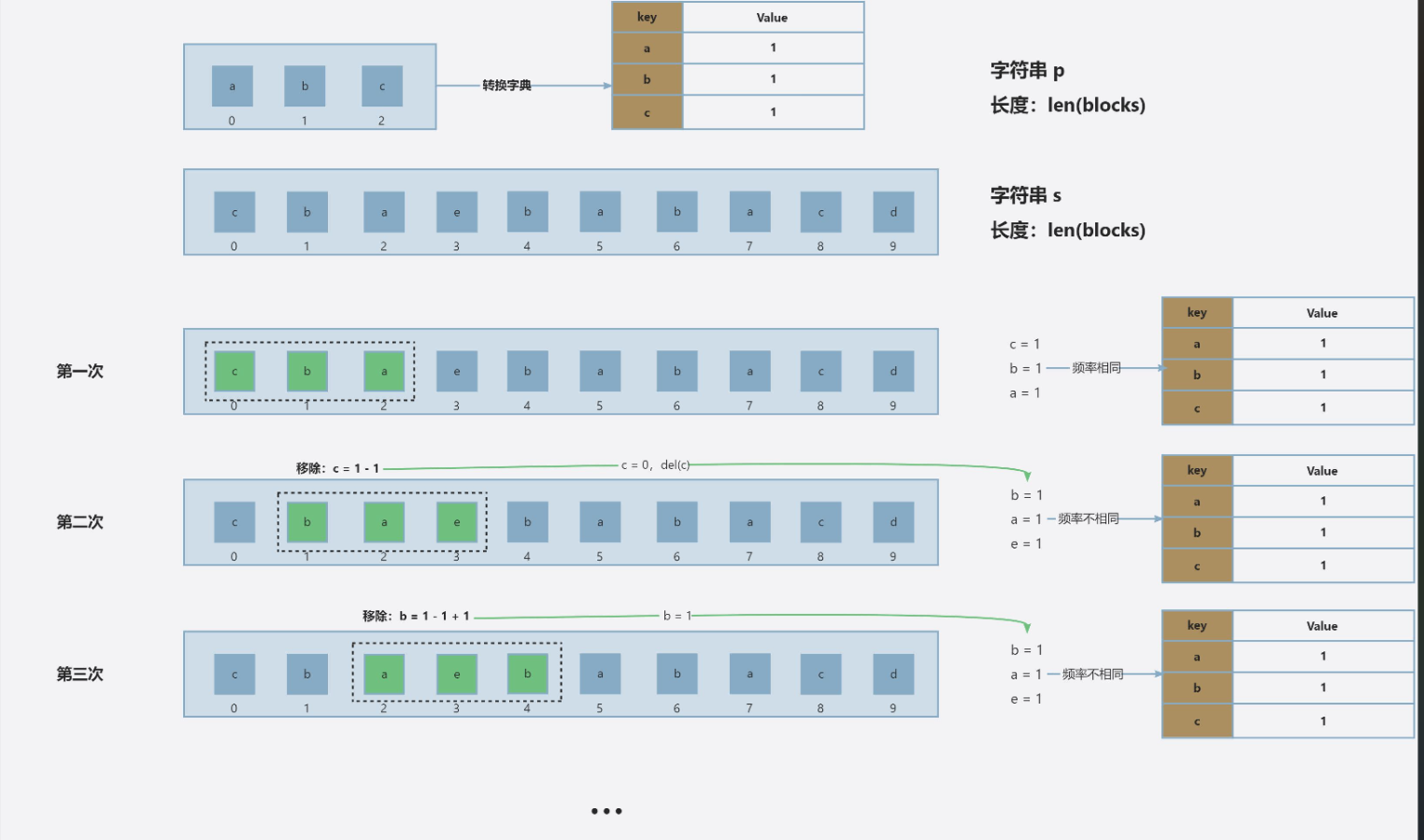
基本思路：使用两个指针left和right来维护一个固定长度的窗口，窗口大小为给定的长度len。每次将right指针向右移动一个位置，将新元素加入窗口，同时判断窗口长度是否超过len，若超过则将left指针向右移动一个位置，移除窗口内的旧元素。通过这种方式，滑动窗口可以遍历字符串中所有长度为所有长度为len 的子串。

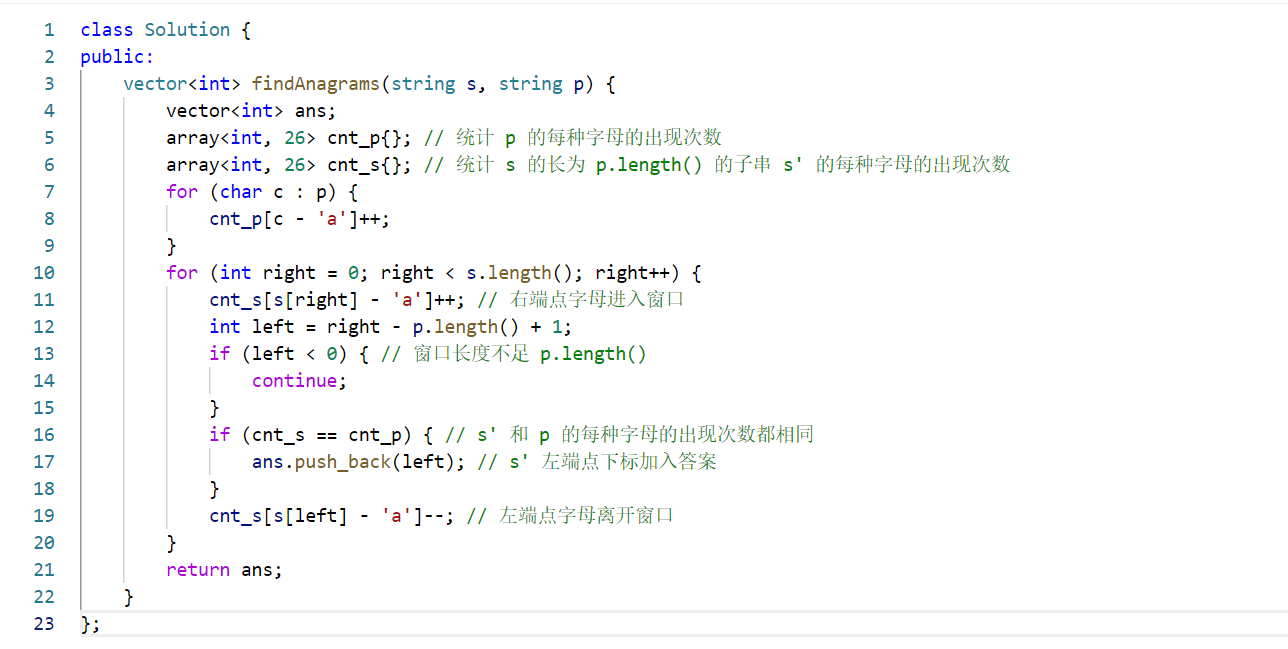
完整代码

方法二：不定长滑窗

核心设计思想

要判断两个字符串是否为异位词，最直接的方法是比较它们的字符计数（每个字符出现的次数是否完全相同）。但如果对每个可能的子串都重新计算计数，效率会很低（时间复杂度 O (n*m)，n 是s长度，m是p长度）。

这个算法的优化点在于：

用滑动窗口固定子串长度（等于p的长度），避免重复检查无效长度的子串。
用哈希表（数组） 记录字符计数，通过增量更新计数（只调整窗口边缘的字符），将每次窗口移动的计算成本从 O (m) 降到 O (1)。

我们定义一个变量 count 来统计窗口中有效字符的个数

如下图所示，当 c 进入窗口之后，与 hash1 中 c 字符出现的次数比较，有两种情况。

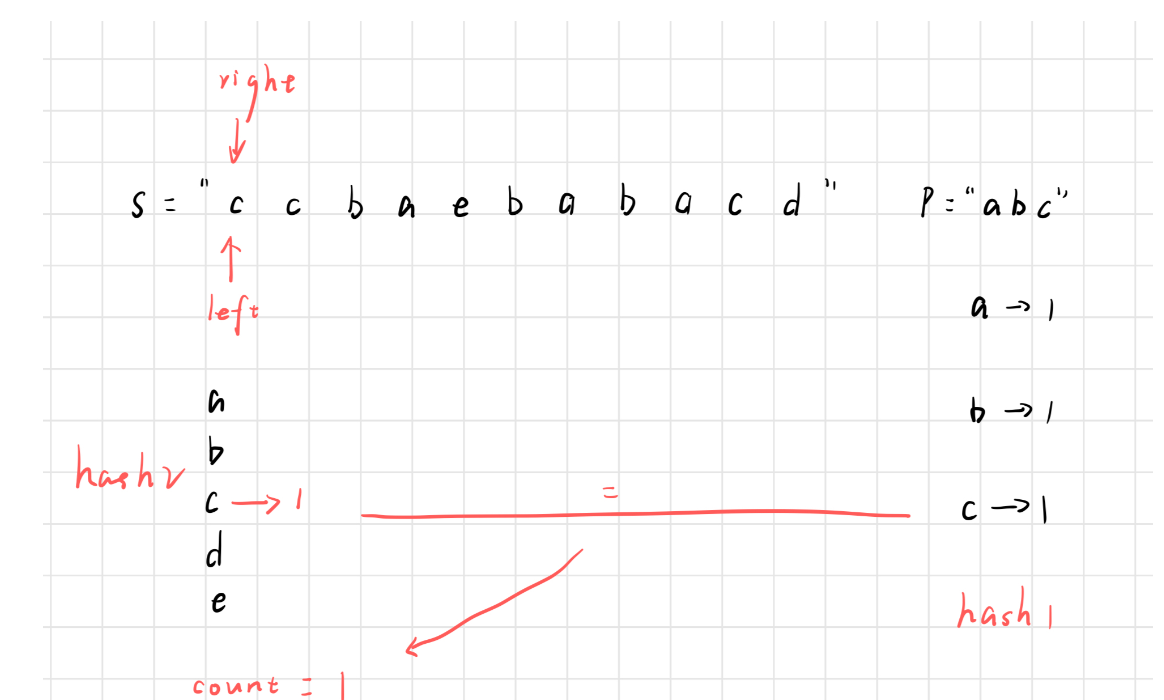
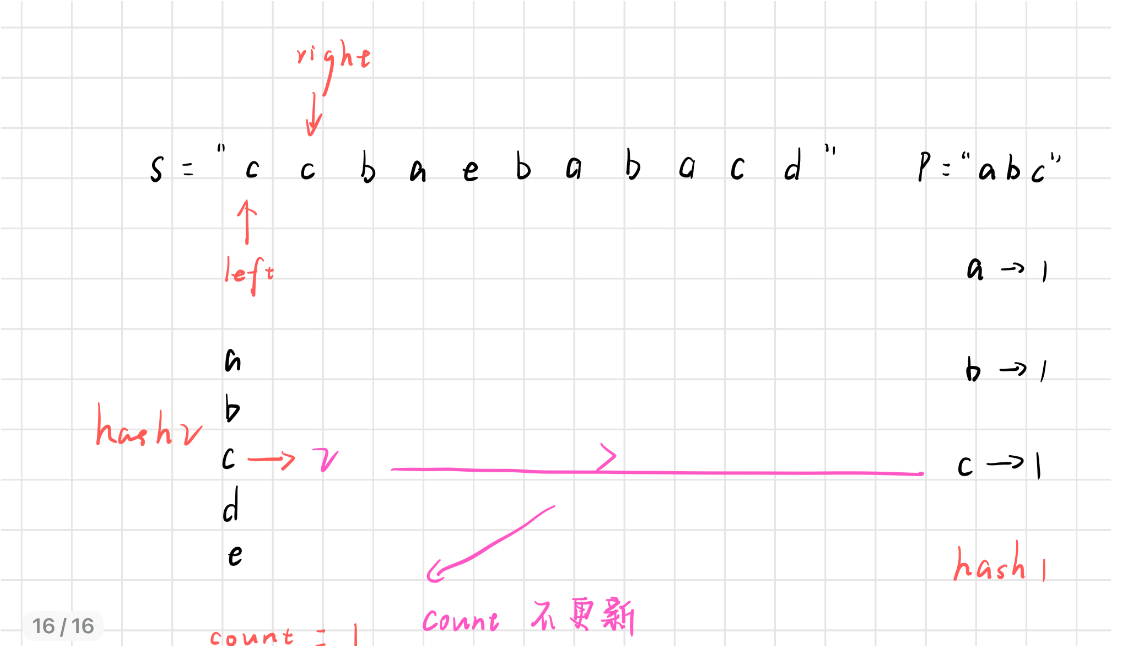
接下来，right 右移

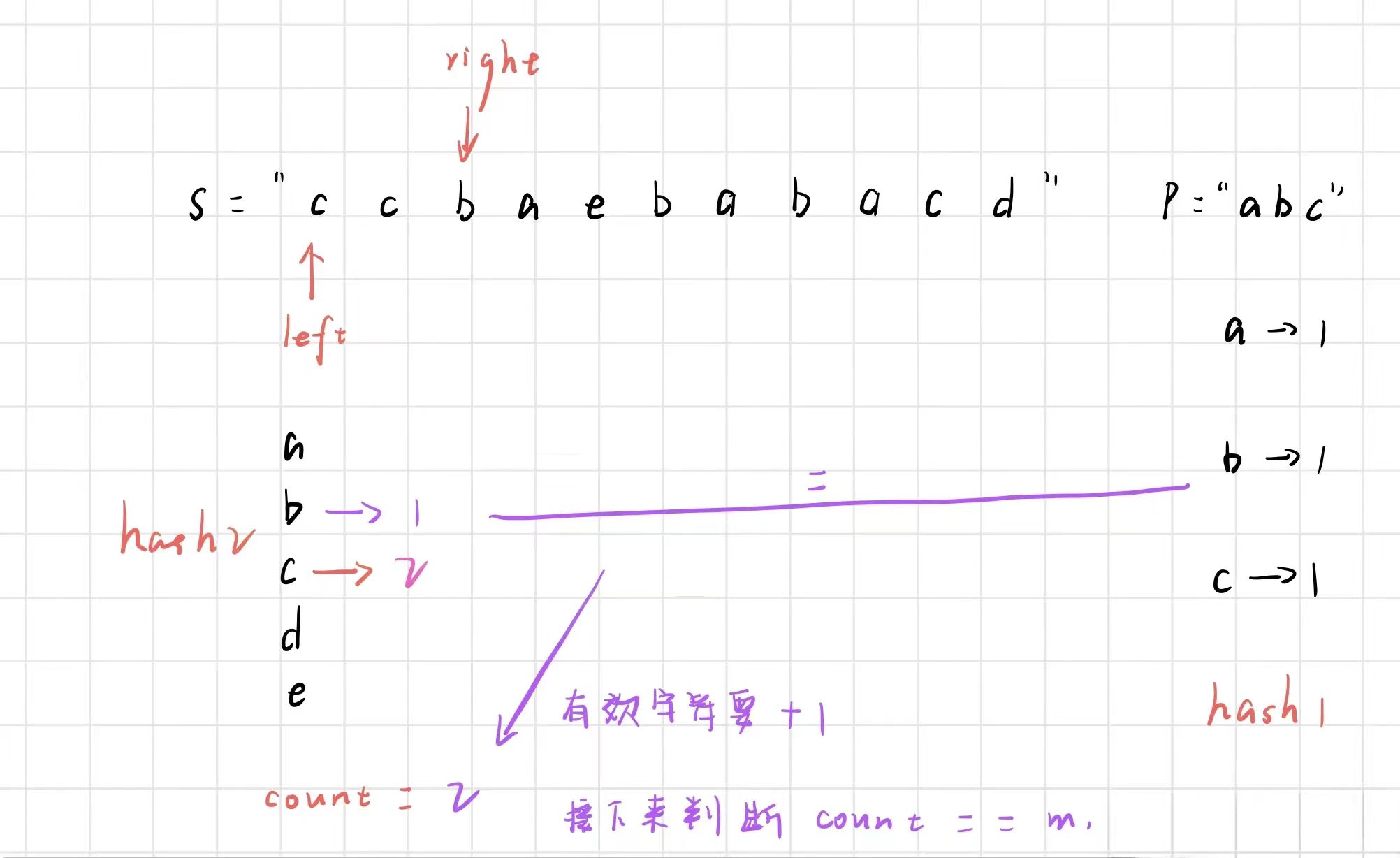
right 继续右移

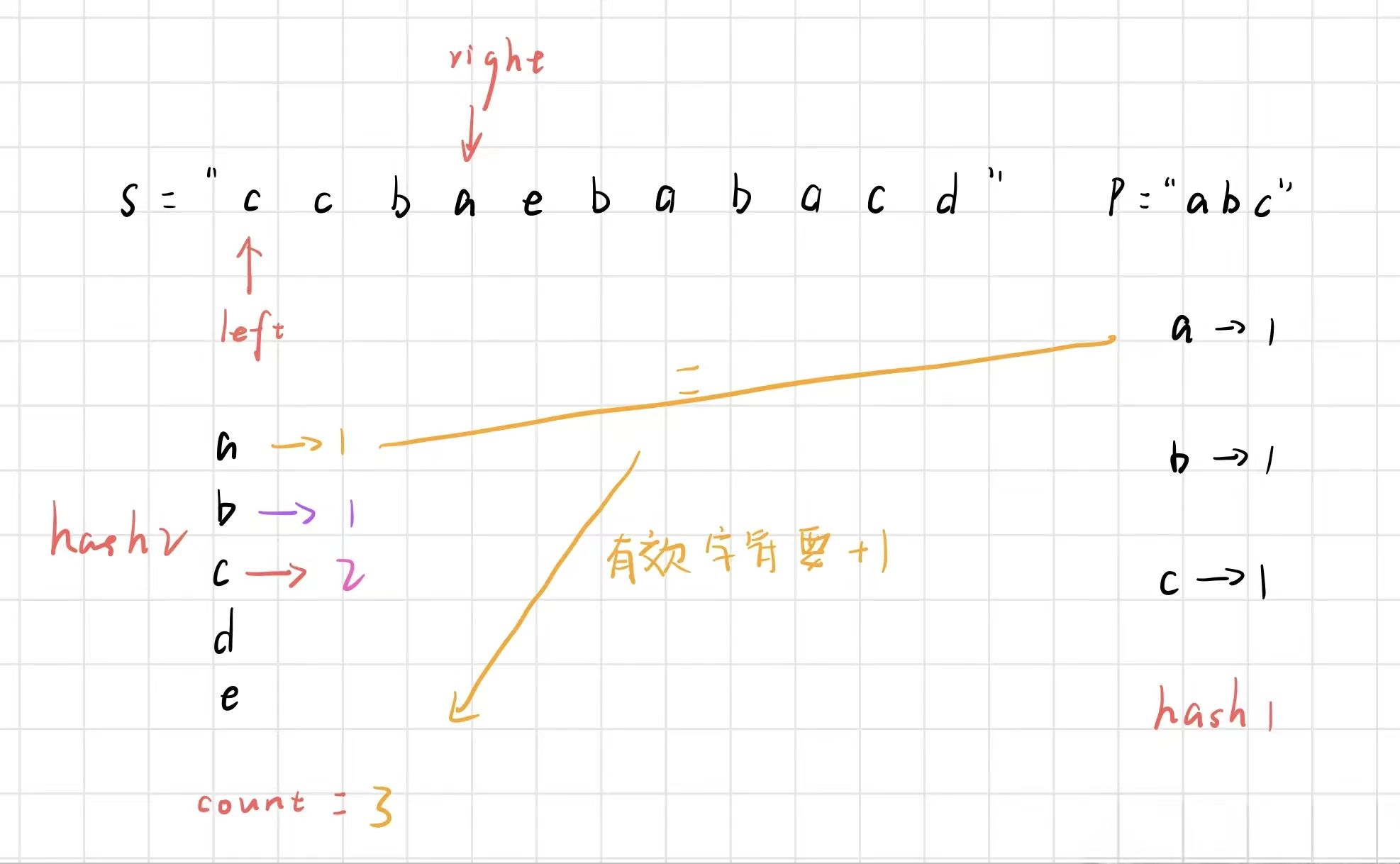
此时，窗口大于 m ，让 left 右移，再将第一个 c 从 hash2 中删除之前，我们要先判断此时这个字符出现的次数是否大于 hash1 中的次数，这种情况，显然是大于，那么删掉的就是无效字符，count 不需要变化，此时 c 的个数变成了 1。

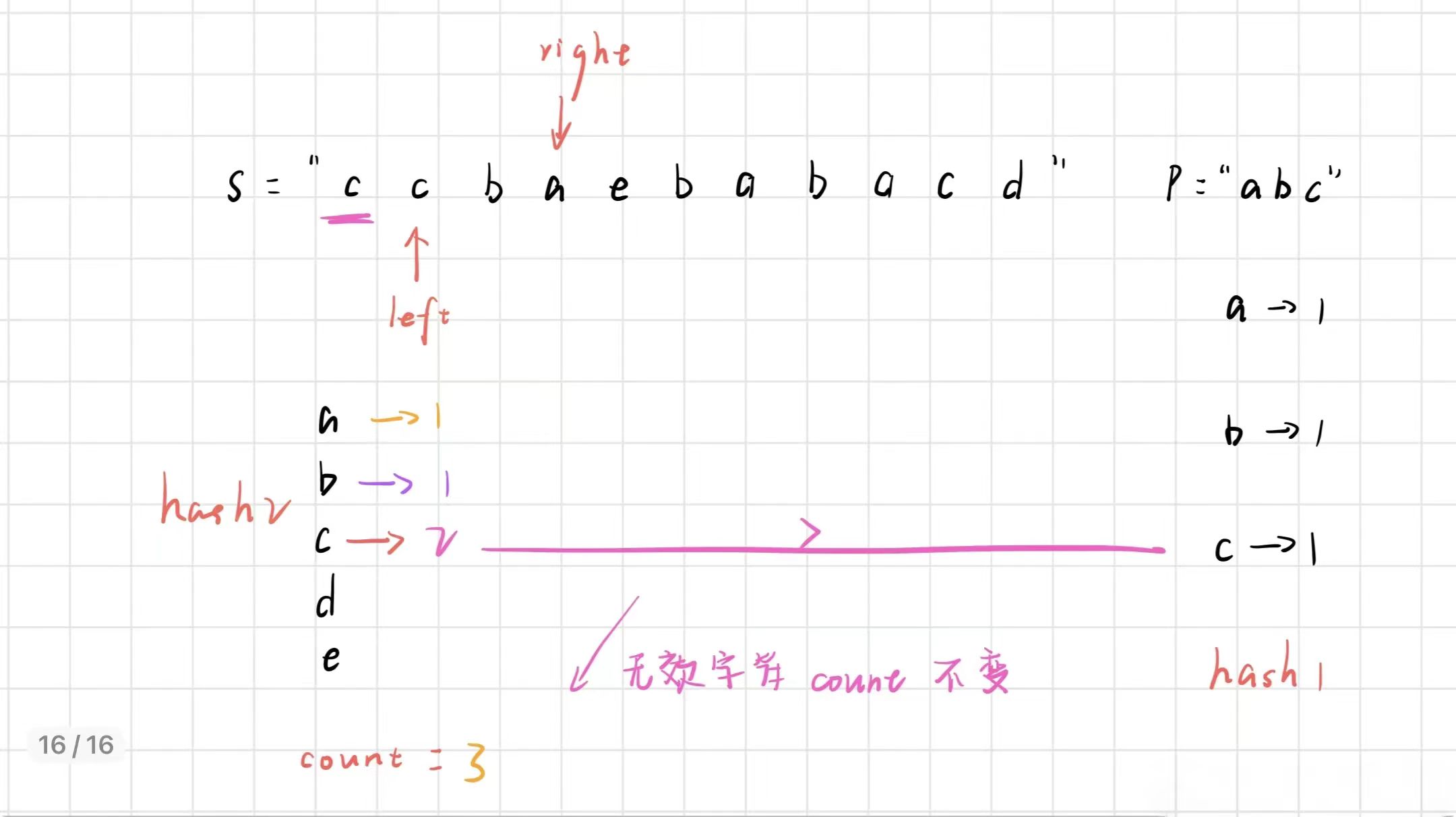
然后我们再判断 count是否等于m，此时count == m，那么窗口中的字符就是 p 的异位词，输出起始位置下标

小于等于 hash1 中的……，说明 c 为有效字符，让 count + 1
之后 right 继续右移，然后放入到 hash2 中
大于 hash1 中的……，count 不更新

接下来的遍历就省略了

进窗口：hash2[in] <= hash1[in] ——> count++
出窗口：hash2[out] <= hash1[out] ——> count–
更新结果：count==m

逐行代码深度解析

1. 初始化哈希表

int hash1[26] = {0};  // 存储 p 中每个字符的出现次数
for (auto ch : p) {hash1[ch - 'a']++;  // 映射字符到数组索引（如 'a'→0, 'b'→1）
}
int hash2[26] = {0};  // 存储当前窗口中每个字符的出现次数

hash1 是固定的，提前计算p中所有字符的计数（例如 p="abc" 时，hash1[0]=1（'a'）、hash1[1]=1（'b'）、hash1[2]=1（'c'））。
hash2 是动态的，会随着窗口滑动实时更新当前窗口的字符计数。

2. 核心变量定义

vector<int> ret;  // 结果数组，存储异位词的起始索引
int m = p.size();  // p 的长度（窗口的固定长度）
int count = 0;     // 记录当前窗口中「有效匹配」的字符数量

count 是算法的「点睛之笔」：它不直接比较两个哈希表，而是通过计数有效匹配的字符数，快速判断窗口是否符合条件。

3. 滑动窗口主循环

循环变量 left 和 right 分别表示窗口的左右边界，初始都为 0，right 负责向右扩展窗口，left 负责在窗口过长时收缩

步骤 1：右指针移动，加入新字符

char in = s[right];  // 当前要加入窗口的字符
if (++hash2[in - 'a'] <= hash1[in - 'a']) {count++;  // 有效匹配数 +1
}

例：p="abc"（hash1[a]=1），窗口中已有 1 个 'a'，再加入 1 个 'a' 时，hash2[a] 变为 2，超过 hash1[a]，count 不增加。

先将 hash2 中该字符的计数 +1（因为字符加入窗口）。
判断：如果加 1 后，hash2 的计数 ≤ hash1 的计数，说明这个字符是「有效匹配」（没有超出p中该字符的数量），因此 count 增加。
反之（如果加 1 后超过hash1的计数），说明这个字符在窗口中过多，不算有效匹配，count 不变。

步骤 2：窗口过长时，左指针移动，移除左侧字符

if (right - left + 1 > m) {  // 窗口长度超过 p 的长度时char out = s[left++];  // 要移除的字符，左指针右移if (hash2[out - 'a']-- <= hash1[out - 'a']) {count--;  // 有效匹配数 -1}
}

当窗口长度超过m（p的长度），需要收缩左边界，保持窗口长度为m。
先记录要移除的字符 out，然后将 hash2 中该字符的计数 -1（因为字符离开窗口）。
判断：如果减 1 前，hash2 的计数 ≤ hash1 的计数，说明这个字符原本是「有效匹配」，移除后有效匹配数减少，因此 count 减少。
反之（如果减 1 前已经超过hash1的计数），说明这个字符原本就不是有效匹配，移除后 count 不变。

例：p="abc"（hash1[a]=1），窗口中原有 2 个 'a'（hash2[a]=2），移除 1 个后变为 1。由于移除前 hash2[a] > hash1[a]，所以 count 不变。

步骤 3：判断是否为异位词，记录结果

if (count == m) {ret.push_back(left);  // 记录起始索引
}

当 count 等于 m（p的长度）时，说明窗口中所有字符的数量都与p完全匹配（每个字符的计数都 ≤ p 且总和为m），因此当前窗口是p的异位词。
此时窗口的起始索引是 left，加入结果数组

完整代码

为什么这个算法高效？

时间复杂度 O (n)：s 中的每个字符只被 right 和 left 各访问一次，每次操作（更新哈希表、判断 count）都是 O (1)。
空间复杂度 O (1)：仅用两个固定大小的数组（26 个元素），与输入规模无关。
避免冗余计算：通过增量更新哈希表，不需要每次重新计算整个窗口的字符计数。