当前位置：首页 > news >正文

Leetcode 深度优先搜索 (7)

news 2025/8/20 7:53:52

Leetcode 深度优先搜索 (7)

给定一个二叉树 root ，返回其最大深度。二叉树的最大深度是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：
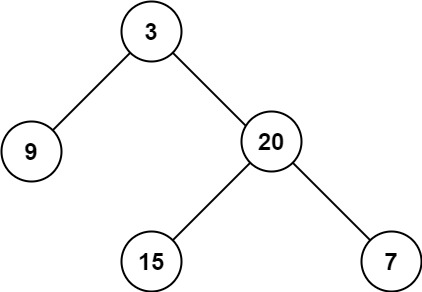
在这里插入图片描述
输入： root = [3,9,20,null,null,15,7]
输出： 3

递归法（深度优先遍历DFS）

如果当前节点为空，最大深度为0。
递归计算左子树和右子树的最大深度。
当前节点的最大深度为左右子树最大深度的较大值加1。

class Solution {public int maxDepth(TreeNode root) {if (root == null) return 0;int leftDepth = maxDepth(root.left);int rightDepth = maxDepth(root.right);return Math.max(leftDepth, rightDepth) + 1;}}

迭代法（广度优先遍历BFS，层序遍历）
使用迭代法求二叉树最大深度的核心思路是：

使用队列，每次将同一层的所有节点入队。
遍历一层，深度加1。
队列为空时，遍历结束，深度即为最大深度。

class Solution {public int maxDepth(TreeNode root) {if (root == null) return 0;Queue<TreeNode> queue = new LinkedList<>();queue.add(root);int depth = 0;while (!queue.isEmpty()) {int size = queue.size();// 遍历当前层的所有节点for (int i = 0; i < size; i++) {TreeNode node = queue.poll();if (node.left != null) queue.add(node.left);if (node.right != null) queue.add(node.right);}depth++;}return depth;}
}

优化递归（记忆化）
记忆化递归优化的核心思路是：

用哈希表（如 Map）记录每个节点的最大深度，避免重复计算。
适用于有重复子树的场景。

    private Map<TreeNode, Integer> memo = new HashMap<>();public int maxDepth(TreeNode root) {if (root == null) return 0;if (memo.containsKey(root)) return memo.get(root);int left = maxDepth(root.left);int right = maxDepth(root.right);int depth = Math.max(left, right) + 1;memo.put(root, depth);return depth;}

Morris遍历（空间优化）
Morris遍历求最大深度的基本思路如下：

当当前节点不为空时：
如果当前节点没有左子树，当前深度+1，更新最大深度，然后移动到右子节点。
如果有左子树，找到左子树的最右节点（前驱节点）：
如果前驱节点的右指针为空，将其指向当前节点（建立线索），当前深度+1，移动到左子节点。
如果前驱节点的右指针指向当前节点（说明左子树已访问完），断开线索，当前深度-1，移动到右子节点。
遍历结束后，返回最大深度。

public int maxDepth(TreeNode root) {int maxDepth = 0;int currentDepth = 0;TreeNode cur = root;while (cur != null) {if (cur.left == null) {currentDepth++;maxDepth = Math.max(maxDepth, currentDepth);cur = cur.right;} else {TreeNode pre = cur.left;int steps = 1;while (pre.right != null && pre.right != cur) {pre = pre.right;steps++;}if (pre.right == null) {pre.right = cur;currentDepth++;maxDepth = Math.max(maxDepth, currentDepth);cur = cur.left;} else {pre.right = null;cur = cur.right;currentDepth -= steps;}}}return maxDepth;}

并行计算（多线程/分治）

并行计算二叉树最大深度可以利用多线程分别计算左右子树的最大深度，然后在主线程中合并结果。具体步骤如下：

如果当前节点为空，返回0。
于非空节点，分别为左子树和右子树创建独立的线程（或任务），并行计算它们的最大深度。
等待左右子树的计算结果，取最大值加1（加上当前节点）。
可以使用Java的线程池（如ForkJoinPool）来高效管理并行任务。

 static class MaxDepthTask extends RecursiveTask<Integer> {private final TreeNode node;MaxDepthTask(TreeNode node) {this.node = node;}@Overrideprotected Integer compute() {if (node == null) return 0;MaxDepthTask leftTask = new MaxDepthTask(node.left);MaxDepthTask rightTask = new MaxDepthTask(node.right);leftTask.fork(); // 异步计算左子树int right = rightTask.compute(); // 当前线程计算右子树int left = leftTask.join(); // 等待左子树结果return Math.max(left, right) + 1;}}public static int maxDepth(TreeNode root) {ForkJoinPool pool = new ForkJoinPool();return pool.invoke(new MaxDepthTask(root));}