【LeetCode】3655. 区间乘法查询后的异或 II (差分/商分 + 根号算法)
3655. 区间乘法查询后的异或 II
题目: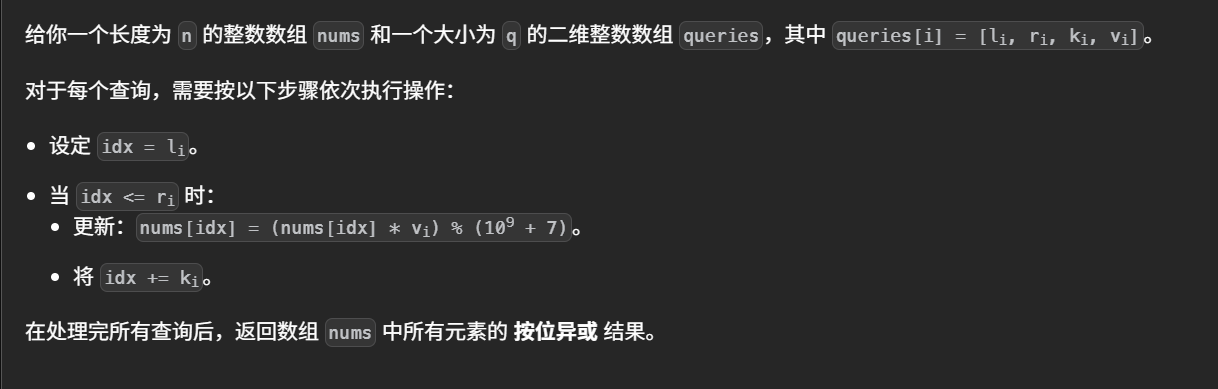
思路:
其实像这种根号算法有个很显然的特征,就是会有一个类似跳跃的功能,如每隔 k 格跳一次
本题不难看出可以使用根号算法讨论,先来看看简单的暴力
对于暴力部分我们直接模拟即可,那么一次询问的时间复杂度为 O(n / k),即跳跃这么多次
那么对于非暴力做法怎么写呢?我们先假设 k = 1,对于区间操作,我们不难想到一个做法,即差分数组,那么本题我们可以类比差分,我们可以做一个 “商分”
具体的,我们初始每一个数初始化为 1,那么每一个位置就是从加变成了乘,依次递推过去即可,而原来的减法我们就要变成除法,但是显然直接除是不行的,注意到题目中要取模,所以我们可以考虑使用乘以逆元的操作来代替除法
那么假如 k > 1 呢?那么我们还是一样的,只不过这次从 每次加一递推 变成了 每次加 k 的递推 了,具体的我们还是一样的乘法操作,但是 r 需要改变,我们在 k 等于 1 时是在 r 处加 1,而这里则是在最后一个合法位置加 k,其实也是类比 k = 1 的情况
那么如何计算呢?不难看出,我们只需要看看 r 需要往后退几格即可,减去这个数后加上 k 就是最后的 r 了
k > 1 的累加过程有点不一样,由于我们设置了间隔,那么我们每次的起点就要设置多个了,即设置 0 ~ k-1,否则就不能统计完所有的数的操作了
最后优化细节就是我们可以判断这个 k 有没有出现过,如果没出现那么就跳过,同时记得开一下 long long,防止运算中爆了
代码:
class Solution {
public:const int MOD = 1e9 + 7;long long qp(long long a, int b) {long long res = 1;a %= MOD;while (b) {if (b & 1)res = res * a % MOD;b >>= 1;a = a * a % MOD;}return res;}int xorAfterQueries(vector<int>& nums, vector<vector<int>>& queries) {int B = sqrt(queries.size());int n = nums.size();vector<vector<int>> dif(B + 1);for (auto& q : queries) {long long l = q[0], r = q[1], k = q[2], v = q[3];if (k >= B) {for (int i = l; i <= r; i += k) {nums[i] = nums[i] * v % MOD;}} else {dif[k].resize(n+k,1);r = r - (r - l) % k + k;dif[k][l] = dif[k][l] * v % MOD;if (r < n)dif[k][r] = dif[k][r] * qp(v, MOD - 2) % MOD;}}for (int k = 1; k < B; k++) {if(dif[k].empty()) continue;for (int start = 0; start < k; start++) {long long sumdiff = 1;for (int i = start; i < n; i += k) {sumdiff = (sumdiff * dif[k][i]) % MOD;nums[i] = nums[i] * sumdiff % MOD;}}}return reduce(nums.begin(), nums.end(), 0, bit_xor());}
};