计算机组成原理(9) - 整数的乘除法运算
计算机中整数的乘除法运算与数学中的乘除法原理类似,但受限于硬件结构(如寄存器位数、运算单元设计),其底层实现需要通过特定的算法和硬件逻辑完成。
一、整数乘法运算
计算机中的整数乘法以二进制为基础,核心是通过 “移位 + 加法” 模拟乘法过程,再结合硬件优化提升效率。
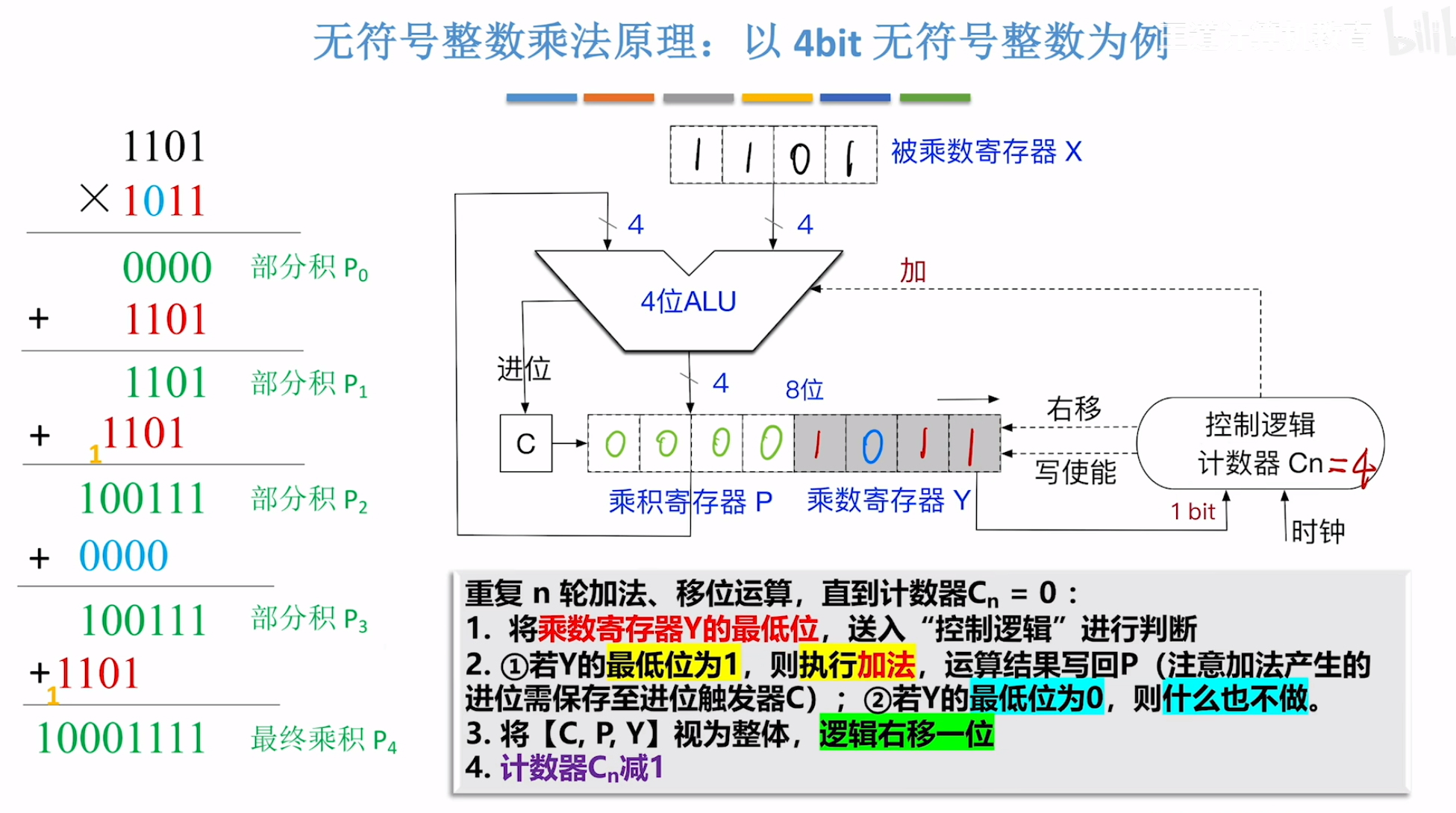
1. 无符号整数乘法:移位相加法
二进制乘法的本质是 “部分积累加”,与十进制乘法类似。例如计算 1010(10)× 0110(6):
1010
× 0110
------0000 (1010 × 0,左移0位)1010 (1010 × 1,左移1位)
1010 (1010 × 1,左移2位)
0000 (1010 × 0,左移3位)
------
111100 (累加结果:60)硬件实现时,步骤如下:
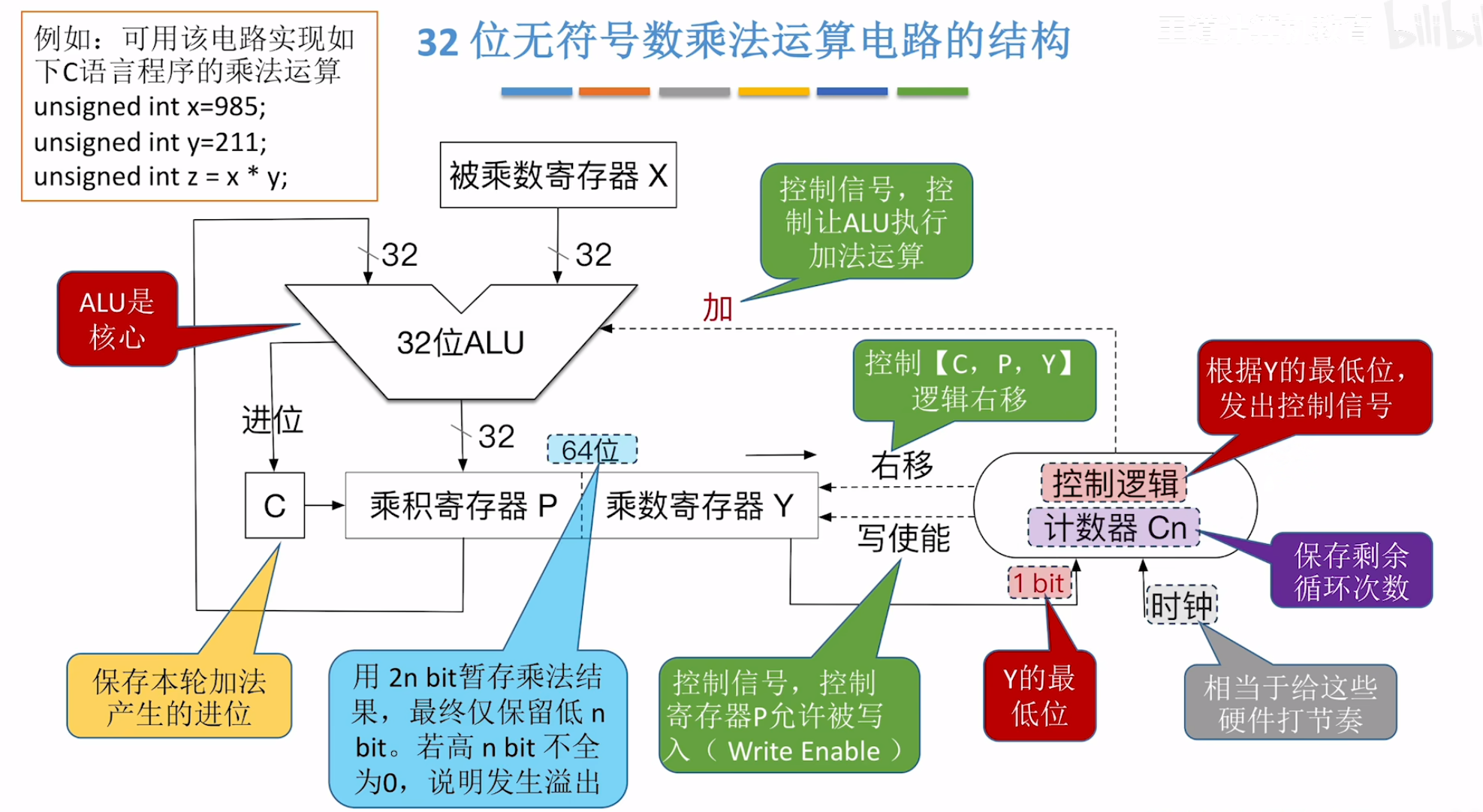
- 初始化:用一个寄存器存储被乘数(
M),一个寄存器存储乘数(Q),一个累加器(A)初始化为 0,总结果位数为M位数 + Q位数(如 32 位 ×32 位 = 64 位结果)。 - 迭代运算:对乘数的每一位(从最低位开始):
- 若当前位为 1,则将被乘数左移对应位数后加到累加器;
- 若为 0,则累加器不变;
- 结果整合:累加器的值即为最终乘积。
2. 有符号整数乘法:补码乘法
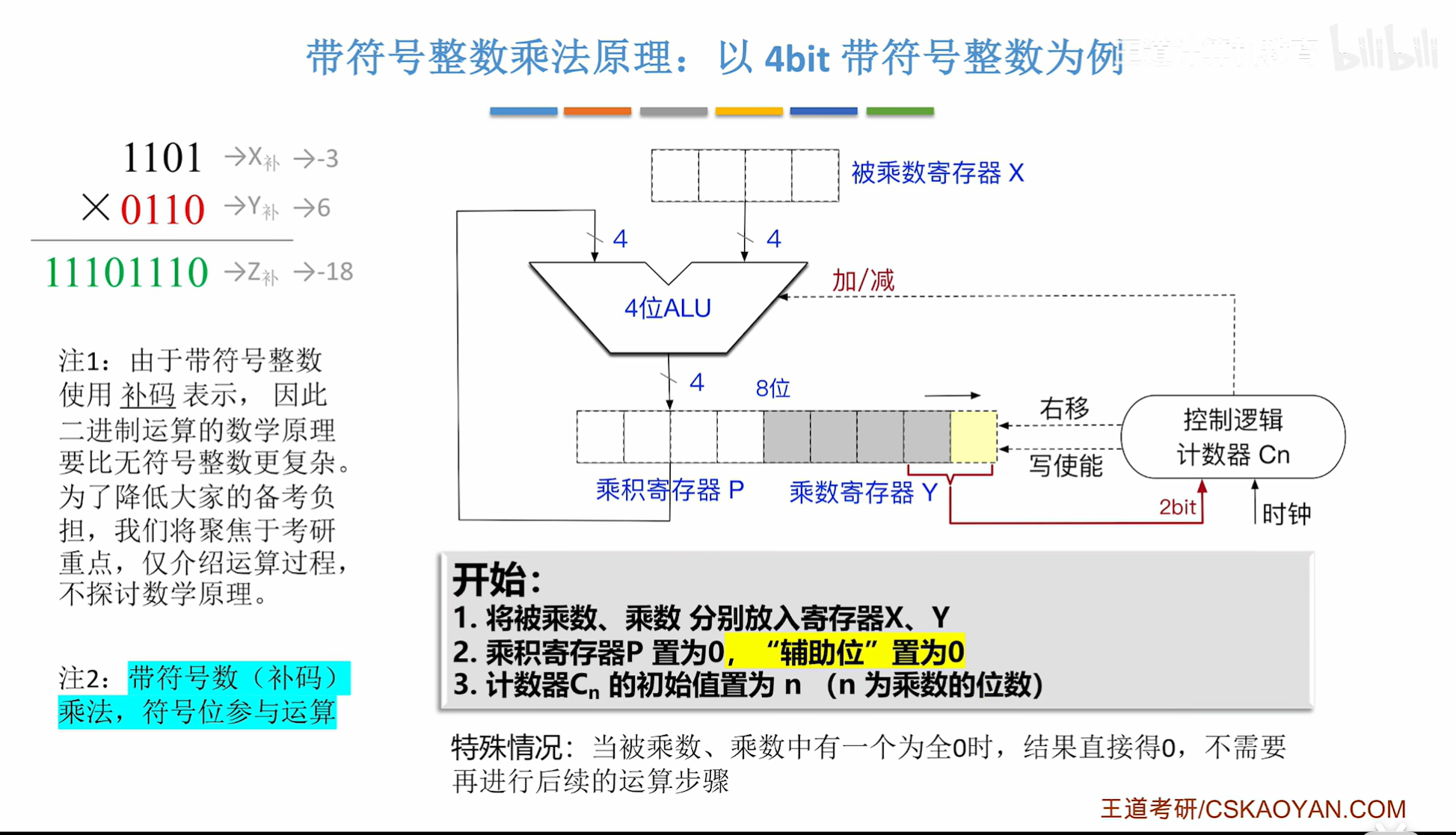
计算机中整数通常用补码表示,有符号数的乘法需要处理符号位。常见方法有两种:
- 符号位单独处理:先计算绝对值的乘积,再根据乘数和被乘数的符号(同号为正,异号为负)确定结果符号。
- 布斯算法(Booth's Algorithm):直接对补码进行运算,无需单独处理符号,优化了运算步骤(尤其适合乘数中连续 0 或 1 较多的场景)。
硬件乘法器结构
- 组合逻辑乘法器:用大量加法器并行计算所有部分积,速度快但硬件成本高(适合低位数乘法,如 8 位 ×8 位)。
- 时序逻辑乘法器:通过移位寄存器和加法器分步骤迭代计算,硬件简单但耗时较长(需
n个周期完成n位乘法)。 - 现代优化:高性能处理器(如 x86、ARM)采用 “Wallace 树” 或 “Dadda 树” 结构,通过并行累加部分积缩短延迟,32 位乘法可在 1-3 个时钟周期内完成。
二、整数除法运算
除法是乘除法中更复杂的运算,核心是 “减去除数并迭代求商”,硬件实现需处理余数、商的生成及溢出问题。
1. 无符号整数除法:恢复余数法与加减交替法
除法的本质是 “重复减去除数,统计次数”,但直接减法效率低,硬件中常用优化算法:
(1)恢复余数法
步骤:
- 初始化:被除数存于寄存器
A(高位)和Q(低位,商的存储位置),除数存于B,A初始为 0。 - 迭代(共
n次,n为除数位数):- 将
A-Q整体左移 1 位(相当于被除数左移,高位进入A); - 若
A ≥ B,则商的当前位(Q的最低位)置 1,A = A - B; - 若
A < B,则商的当前位置 0,A保持不变(“恢复” 余数)。
- 将
示例:10(1010)÷ 3(0011),最终商为 3(0011),余数为 1(0001)。
(2)不恢复余数法(加减交替法)
优化恢复余数法的冗余步骤:
- 若当前余数
A ≥ 0,商的当前位置 1,左移后减去除数(A = (A << 1) - B); - 若当前余数
A < 0,商的当前位置 0,左移后加上除数(A = (A << 1) + B); - 最终若余数为负,需加除数恢复正确余数。
该方法无需 “恢复” 余数,步骤更简洁,是硬件除法的主流实现方式。
(2)不恢复余数法(加减交替法)
优化恢复余数法的冗余步骤:
- 若当前余数
A ≥ 0,商的当前位置 1,左移后减去除数(A = (A << 1) - B); - 若当前余数
A < 0,商的当前位置 0,左移后加上除数(A = (A << 1) + B); - 最终若余数为负,需加除数恢复正确余数。
该方法无需 “恢复” 余数,步骤更简洁,是硬件除法的主流实现方式。
2. 有符号整数除法
与乘法类似,有符号数除法需处理符号
- 符号位规则:商的符号 = 被除数符号 ⊕ 除数符号(同号为正,异号为负);余数符号与被除数相同。
- 运算过程:先将被除数和除数取绝对值运算,再根据符号规则调整商和余数的符号。
例如:(-10) ÷ 3,绝对值运算得商 3、余数 1,最终商为 -3,余数为 -1(与被除数同号)。
3. 除法中的特殊问题与处理
- 溢出:当商超过结果寄存器的最大表示范围时(如
32位除法中,商 > 2^31-1),硬件会触发溢出标志(OF),通常通过异常处理(如程序中断)。 - 除数为 0:硬件无法计算,会触发除法错误异常(如 x86 的
#DE异常),由操作系统捕获处理(如终止程序)。 - 余数处理:整数除法默认 “向零取整”(如
5 ÷ 2 = 2,-5 ÷ 2 = -2),部分场景需特殊处理(如四舍五入)时需软件额外计算。
