当前位置：首页 > news >正文

牛客周赛 Round 105（小苯的xor构造/小苯的权值计算/小苯的01矩阵构造/小苯的重排构造/小苯的xor图/小苯的前缀gcd构造）

news 2025/8/19 16:41:10

小苯的xor构造

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long 
using namespace std;
int n;
int main(){ios::sync_with_stdio(false);        // 禁用同步cin.tie(nullptr);                   // 解除cin与cout绑定cin >> n;cout << 0 << " " << n;return 0;
}

小苯的权值计算

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long 
using namespace std;
int n;
int gcd(int q, int p) {while (q % p != 0) {int w = p;p = q % p;q = w;}return p;
}
int main(){ios::sync_with_stdio(false);        // 禁用同步cin.tie(nullptr);                   // 解除cin与cout绑定cin >> n;vector<int> a(n), b(n - 1);for (int i = 0; i < n; i++) {cin >> a[i];}for (int i = 0; i < n - 1; i++) {b[i] = a[i] ^ a[i + 1];}int ans = b[0];for (int i = 1; i < n - 1; i++) {ans = gcd(ans, b[i]);}cout << ans << endl;return 0;
}

小苯的01矩阵构造

思路：

多举一些样例就可以看出k 为奇数时不存在。

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long 
using namespace std;
int n, k;
int main(){ios::sync_with_stdio(false);        // 禁用同步cin.tie(nullptr);                   // 解除cin与cout绑定cin >> n >> k;if (k % 2 == 1) {cout << -1 << endl;}else {for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (i != j) {cout << 0;}else {if (k > 0) {cout << 1;k -= 2;}elsecout << 0;}}cout << endl;}}return 0;
}

小苯的重排构造

核心思路

统计 1 和 2 的数量
遍历输入数组，分别统计 1 的个数 a 和 2 的个数 b。
特殊情况处理
- 如果所有元素都是 1，且 k 等于 a-1，则输出全 1 的排列；否则输出 -1。
- 如果所有元素都是 2，且 k 等于 2*(b-1)，则输出全 2 的排列；否则输出 -1。
无效情况判断
- 如果 k 小于 n-1（最小可能值）或大于 2*(b-1)+a（最大可能值），直接输出 -1。
- 如果 b > a 且 k < 2*(b-a-1)+a，也输出 -1。
构造有效排列
- 计算 w = k - (n-1)，表示需要额外增加的差值。
- 通过优先输出 2 来消耗 w，每输出一个 2 减少 w 的值。
- 交替输出剩余的 2 和 1，确保排列的合法性。

代码实现逻辑

输入处理：使用快速输入优化，减少读取时间。
统计 a 和 b：遍历输入数组，分别统计 1 和 2 的数量。
边界检查：根据 k 的范围和 a、b 的关系判断是否有解。
构造排列：通过调整 2 的输出顺序来满足 k 的要求，最后交替输出剩余元素。

关键点

差值的计算：相邻 2 的差值为 0，1 和 2 的差值为 1，1 之间的差值为 0。
排列的合法性：确保输出的排列中 1 和 2 的数量与输入一致，且满足 k 的约束条件。

该算法通过贪心策略优先处理 2 的分布，确保差值最大化，再通过交替输出剩余元素满足最小差值条件。

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long 
using namespace std;
int n, k, a = 0, b = 0, q;
int main(){ios::sync_with_stdio(false);        // 禁用同步cin.tie(nullptr);                   // 解除cin与cout绑定cin >> n >> k;for (int i = 0; i < n; i++) {cin >> q;if (q == 1) {a++;}else {b++;}}if (a == n) {if (k == (a - 1)) {for (int i = 0; i < n; i++) {cout << 1 << " ";}cout << endl;}else {cout << -1 << endl;}}else if (b == n) {if (k == 2*(b - 1)) {for (int i = 0; i < n; i++) {cout << 2 << " ";}cout << endl;}else {cout << -1 << endl;}}else if (k < n-1 || k>2 * (b - 1) + a||(b>a&&k<2*(b-a-1)+a)) {cout << -1 << endl;}else {int w = k - n + 1;while (w > 0) {cout << 2 << " ";w -= 1;b--;}while (a > 0 || b > 0) {if (b > 0) {cout << 2 << " ";b--;}if (a > 0) {cout << 1 << " ";a--;}}}return 0;
}

小苯的xor图

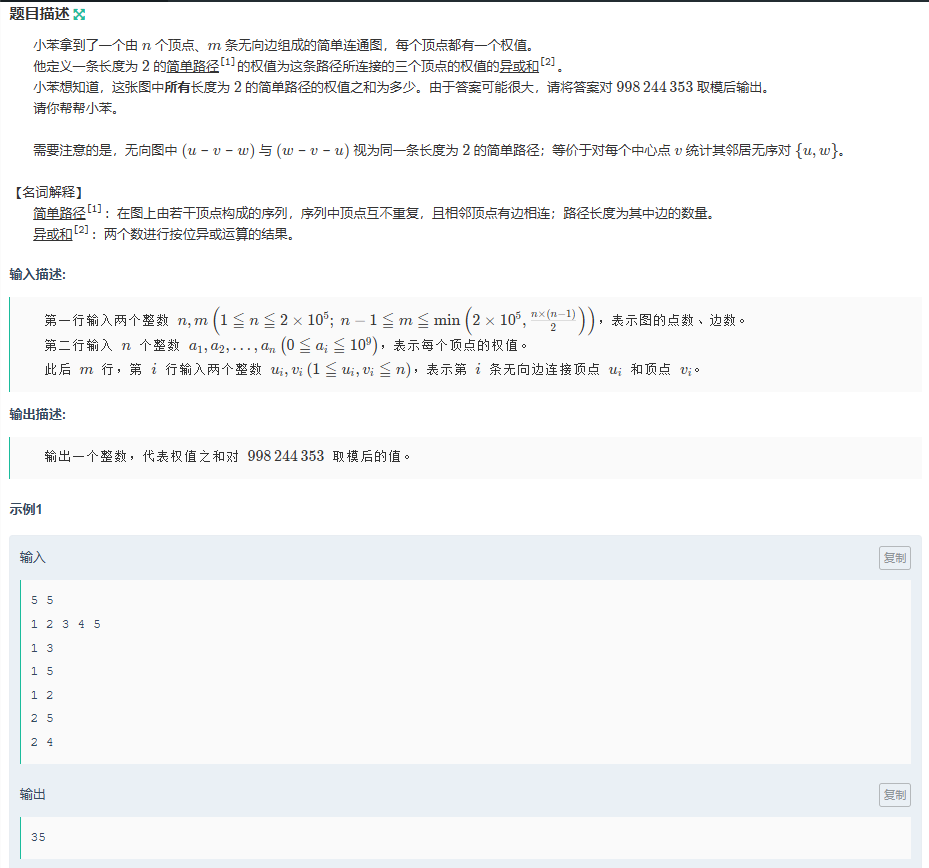
这题关键是拆成二进制来写，暴力超限

核心算法思路

图的表示与输入处理
- 使用邻接表a存储图的边关系。
- 数组head存储每个顶点的初始值。
预处理二进制位统计
- 二维数组cnt[i][z]表示与顶点i相邻的顶点中，head值的第z位为1的数量。
- 遍历每个顶点i及其邻居，分解邻居的head值为二进制，更新cnt[i][z]。
计算贡献值
- 遍历每个顶点i及其二进制位j：
  - 如果head[i]的第j位为0，贡献值为邻居中该位为1的数量乘以为0的数量，再乘以2^j。
  - 如果head[i]的第j位为1，贡献值为邻居中该位相同的顶点对数（组合数）乘以2^j，并除以2（避免重复计算）。
- 使用模运算和逆元（inv2）处理除法。

关键代码段解析

逆元定义
```
ll inv2 = (mod + 1) / 2; // 2的逆元，等价于pow(2, mod-2)
```
用于将除法转换为乘法，满足模运算性质。
二进制位分解与统计
```
for (int z = 0; z <= 31 && q > 0; z++) {if (q % 2 == 1) cnt[i][z]++;q /= 2;
}
```
分解邻居的head值，统计每位为1的数量。

贡献值计算

if (q % 2 == 0) {ans = (ans + (ll)cnt[i][j] * (p - cnt[i][j]) * (1 << j) % mod) % mod;
} else {ll w = ((ll)cnt[i][j] * (cnt[i][j] - 1) * (1 << j) % mod + (ll)(p - cnt[i][j]) * (p - cnt[i][j] - 1) * (1 << j) % mod) % mod;w = w * inv2 % mod;ans = (ans + w) % mod;
}

当前顶点位为0时，贡献为(邻居位1数) × (邻居位0数) × 2^j。
当前顶点位为1时，贡献为C(邻居位1数, 2) + C(邻居位0数, 2)乘以2^j，再除以2。

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long 
using namespace std;
int n, m;
ll ans = 0, mod = 998244353;
ll inv2 = (mod + 1) / 2;//除以2的逆元，也可以是pow(2,mod-1);
int main() {ios::sync_with_stdio(false);        // 禁用同步cin.tie(nullptr);                   // 解除cin与cout绑定cin >> n >> m;vector<int> head(n + 1);vector<vector<int>>a(n + 1);vector <vector<int> >cnt(n + 1,vector<int>(31, 0));for (int i = 1; i <= n; i++) {cin >> head[i];}int l, r;for (int i = 0; i < m; i++) {cin >> l >> r;a[l].push_back(r);a[r].push_back(l);}for (int i = 1; i <= n; i++) {for (int j = 0; j < a[i].size(); j++) {int q = head[a[i][j]];for (int z = 0; z <= 31 && q > 0; z++) {if (q % 2 == 1) {cnt[i][z]++;}q /= 2;}}}for (int i = 1; i <= n; i++) {int q = head[i], p = a[i].size();for (int j = 0; j < 31; j++) {if (q > 0) {if (q % 2 == 0) {ans = (ans + (ll)cnt[i][j] * (p - cnt[i][j])*(1<<j)%mod) % mod;}else {ll w = ((ll)cnt[i][j] * (cnt[i][j]-1)*(1<<j) % mod + (ll)(p - cnt[i][j]) * (p - cnt[i][j] - 1) * (1 << j) % mod) % mod;w = w % mod * inv2 % mod;ans = (ans + w) % mod;}q /= 2;}else {ans = (ans + (ll)cnt[i][j] * (p - cnt[i][j]) * (1 << j)%mod) % mod;}}}cout << ans << endl;return 0;
}

//暴力写法（十进制）#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long 
using namespace std;
int n, m;
ll ans = 0, mod = 998244353;
int main(){ios::sync_with_stdio(false);        // 禁用同步cin.tie(nullptr);                   // 解除cin与cout绑定cin >> n >> m;vector<int> head(n + 1);vector<vector<int>>a(n + 1);for (int i = 1; i <= n; i++) {cin >> head[i];}int l, r;for (int i = 0; i < m; i++) {cin >> l >> r;a[l].push_back(r);a[r].push_back(l);}for (int i = 1; i <= n; i++) {int w = head[i];for (int j = 0; j < a[i].size(); j++) {int ww = w ^ head[a[i][j]];for (int z = 0; z < a[a[i][j]].size(); z++) {if (i < a[a[i][j]][z]){int www = ww ^ head[a[a[i][j]][z]];ans = (ans + www) % mod;}}}}cout << ans << endl;return 0;
}

小苯的前缀gcd构造

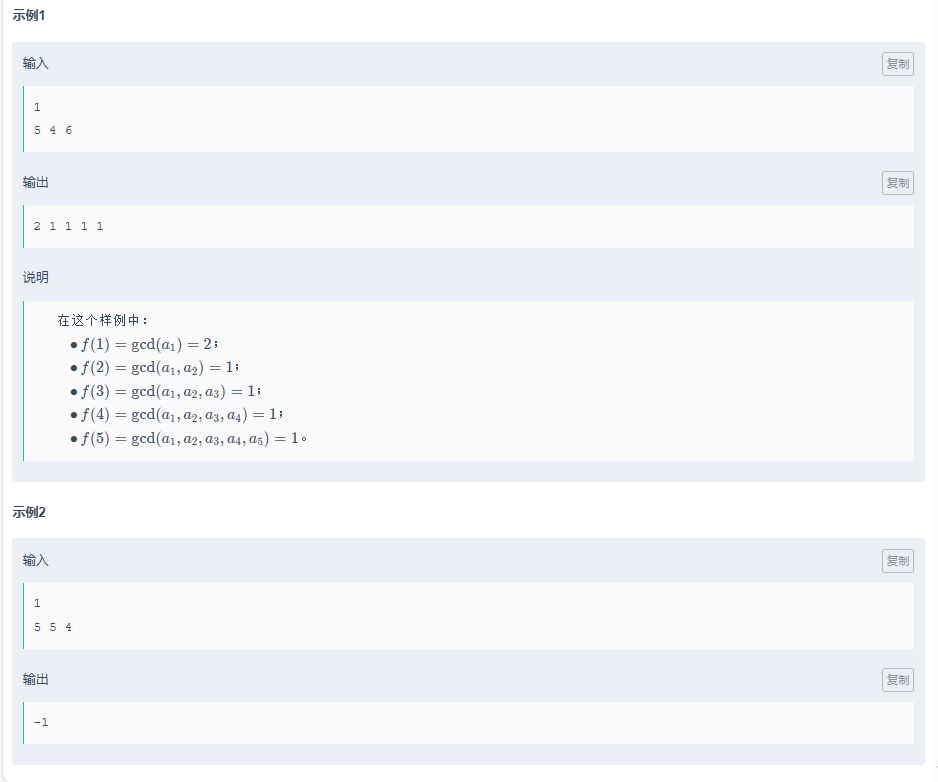
思路：

第一种：BFS

核心思路

状态表示 使用三维数组 visited[i][last][sum] 表示状态：

i：当前处理到序列的第 i 个位置。
last：前 i 个元素的 GCD 值。
sum：前 i 个元素的前缀 GCD 累加和。

BFS 搜索 从初始状态 (0, 0, 0) 开始，通过 BFS 逐步扩展状态：

对于当前状态 (i, last, sum)，尝试所有可能的下一元素 next_a（1 ≤ next_a ≤ m）。
计算新状态 (i+1, new_last, new_sum)，其中：
- new_last 是 last 和 next_a 的 GCD。
- new_sum 是 sum + new_last。
剪枝条件：
- new_sum 不能超过 x。
- 剩余位置的最小和（全选 1）不能使 new_sum 超过 x。
- 剩余位置的最大和（全选 m）不能使 new_sum 小于 x。

路径回溯 如果找到目标状态 (n, last, x)，通过 parent 数组回溯构造序列：

从最终状态倒推，记录每一步选择的 next_a。
反转记录的序列得到最终答案。

剪枝策略

提前终止：如果 sum 超过 x 或剩余位置无法满足条件，跳过该状态。
状态去重：使用 visited 数组避免重复处理相同状态。

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#include <cstring>
#include <tuple>
using namespace std;const int MAX_N = 51;
const int MAX_M = 51;
const int MAX_X = 2501;  // n<=50, m<=50 -> x <= 2500struct State {int i, last, sum;State(int i, int last, int sum) : i(i), last(last), sum(sum) {}
};struct Record {State prev_state;int a_i;Record(State s, int a) : prev_state(s), a_i(a) {}Record() : prev_state(State(0,0,0)), a_i(0) {}
};bool visited[MAX_N][MAX_M][MAX_X];
Record parent[MAX_N][MAX_M][MAX_X];int gcd(int a, int b) {if (b == 0) return a;return gcd(b, a % b);
}void solve() {int n, m, x;cin >> n >> m >> x;if (x < n || x > n * m) {cout << -1 << endl;return;}memset(visited, 0, sizeof(visited));queue<State> q;q.push(State(0, 0, 0));visited[0][0][0] = true;bool found = false;State final_state(0,0,0);while (!q.empty()) {State state = q.front();q.pop();if (state.i == n) {if (state.sum == x) {found = true;final_state = state;break;}continue;}for (int next_a = 1; next_a <= m; next_a++) {int new_last, new_sum;if (state.i == 0) {new_last = next_a;new_sum = next_a;} else {new_last = gcd(state.last, next_a);new_sum = state.sum + new_last;}if (new_sum > x) continue;if (new_sum + (n - state.i - 1) > x) continue;if (new_sum + (n - state.i - 1) * m < x) continue;int new_i = state.i + 1;if (!visited[new_i][new_last][new_sum]) {visited[new_i][new_last][new_sum] = true;parent[new_i][new_last][new_sum] = Record(state, next_a);q.push(State(new_i, new_last, new_sum));}}}if (!found) {cout << -1 << endl;} else {vector<int> ans;State cur = final_state;for (int i = n; i >= 1; i--) {Record& r = parent[cur.i][cur.last][cur.sum];ans.push_back(r.a_i);cur = r.prev_state;}reverse(ans.begin(), ans.end());for (int i = 0; i < ans.size(); i++) {cout << ans[i];if (i < ans.size() - 1) cout << " ";}cout << endl;}
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int t;cin >> t;while (t--) {solve();}return 0;
}

第二种：DFS

核心算法思路

预处理阶段 建立每个数的所有因数的查找表a[51]，其中a[i]存储了i的所有因数（从大到小排列）

主要解决逻辑 采用深度优先搜索(DFS)来寻找符合条件的序列：

计算初始平均值w = x/n
如果x<n直接返回-1（因为每个元素至少为1）
如果x正好能被n整除，直接输出n个w
否则从m开始向下搜索可能的起始值

DFS实现细节

参数k表示当前处理的位置
参数w表示当前位置的值
参数sum表示当前累计和
剪枝条件：
- 剩余元素的最小和(sum + (n-k)*1) > x时放弃
- 剩余元素的最大可能和(sum + (n-k)*w) < x时放弃
递归尝试当前数的所有因数作为下一个元素

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long 
#define endl "\n"
using namespace std;
int n, m, x, t;
vector<vector<int>>a(51);
int b[51];
int gcd(int q, int p) {if (q == 0 || p == 0) {return q == 0 ? p : q;}while (q % p != 0) {int w = p;p = q % p;q = w;}return p;
}
bool dfs(int k, int w, int sum) {b[k] = w;if (k == n && sum != x) {return false;}else if (k == n && sum == x) {return true;}else if (k != n && sum >= x) {return false;}if (x - sum < n - k ) {return false;}else if (x - sum > (n - k) * w) {return false;}for (int i = 0; i < a[w].size(); i++) {if (sum + a[w][i] <= x) {if (dfs(k + 1, a[w][i], sum + a[w][i])) {return true;}}}return false;
}
void solve() {cin >> n >> m >> x;int w = x / n;if (x < n) {cout << -1 << endl;return;}memset(b, 0, sizeof(b));if (w * n == x) {for (int i = 0; i < n; i++) {cout << w << " ";}cout << endl;}else {for (int i = m; i >=w+1; i--) {if(dfs(1, i, i)){for (int i = 1; i <= n; i++) {cout << b[i] << " ";}cout << endl;return;}}cout << -1 << endl;}}
int main() {ios::sync_with_stdio(false);        // 禁用同步cin.tie(nullptr);                   // 解除cin与cout绑定for (int i = 1; i <= 50; i++) {for (int j = i; j >=1; j--) {if (i % j == 0) {a[i].push_back(j);}}}cin >> t;while(t--) {solve();}return 0;
}

查看全文

http://www.lryc.cn/news/625206.html