【DL学习笔记】交叉熵损失函数详解
文章目录
- 一、信息量、熵、交叉熵、相对熵/KL散度、交叉熵损失
- 1、信息量 Amount of Information
- 2、熵 Entropy
- 3、交叉熵 Cross Entropy
- 4、相对熵 Relative Entropy 、KL散度 KL Divergence
- 4、交叉熵损失 Cross Entropy Loss
- 二、交叉熵损失函数
- 交叉熵损失函数拆解
- 代码实现`nn.CrossEntropyLoss`
- 三、二元交叉熵损失函数 Binary Cross Entropy Loss
- 1、二元交叉熵损失函数
- 2、nn.BCELoss() 类
- 3、使用场景举例
- 4、`torch.nn.BCEWithLogitsLoss()` 与 `nn.BCELoss()` 的区别
- 5、`torch.nn.BCEWithLogitsLoss()` 类
| 名称 | 公式 |
|---|---|
| 信息量 | I(x)=log2(1p(x))=−log2(p(x))I(x) = \log_2\left(\frac{1}{p(x)}\right) = -\log_2(p(x))I(x)=log2(p(x)1)=−log2(p(x)) |
| 熵 | H(p)=∑piIip=−∑pilog2(pi)H(p) = \sum p_i I_i^p = -\sum p_i \log_2(p_i)H(p)=∑piIip=−∑pilog2(pi) |
| 交叉熵 | H(p,q)=∑piIiq=−∑pilog2(qi)H(p, q) = \sum p_i I_i^q = -\sum p_i \log_2(q_i)H(p,q)=∑piIiq=−∑pilog2(qi) |
| 相对熵(KL散度) | DKL(p∣∣q)=∑pilog2(piqi)D_{KL}(p \vert \vert q) = \sum p_i \log_2\left(\frac{p_i}{q_i}\right)DKL(p∣∣q)=∑pilog2(qipi) |
| 交叉熵损失函数 | Cross_Entropy_Loss=H(p,q)=−log2(qclass)Cross\_Entropy\_Loss = H(p, q) = -\log_2(q_{class})Cross_Entropy_Loss=H(p,q)=−log2(qclass) |
参考Axure
一、信息量、熵、交叉熵、相对熵/KL散度、交叉熵损失
1、信息量 Amount of Information
- 定义:事件包含的信息量大小(事件发生的难度有多大)
- 小概率事件,它发生的难度比较大,所以有较大的信息量
- 大概率事件,它发生的难度比较小,所以有较小的信息量
这里举个例子
| 事件 | 具体情况 | PPP | 事件类型 | 发生难度 | 信息量 |
|---|---|---|---|---|---|
| 事件A | 小明考试及格 | P(A)=20%P(A)=20\%P(A)=20% | 小概率事件 | 大 | 大 |
| 事件B | 小明考试不及格 | P(B)=80%P(B)=80\%P(B)=80% | 大概率事件 | 小 | 小 |
如果小明考及格了,事件A发生的难度大,可能发愤图强了,可能作弊打小抄了,可能老师打错分了,肯能蒙得全对了…所以事件B发生的背后可能有很多事发生,所以信息量很大;如果B发生了,小明考及格了只是正常发挥,没啥大不了。
- 性质:对于独立事件A、B:p(AB)=p(A)p(B)p(AB) = p(A)p(B)p(AB)=p(A)p(B),两个事件同时发生的信息量等于两个事件的信息量相加:
I(AB)=I(A)+I(B)I(AB) = I(A) + I(B)I(AB)=I(A)+I(B)
- 信息量公式:I(x):=log2(1p(x))=−log2(p(x))I(x) := log_2(\frac{1}{p(x)}) = -log_2(p(x))I(x):=log2(p(x)1)=−log2(p(x))
:=是‘定义为’的意思,不是等号的意思,通常用于定义函数公式- p(x)p(x)p(x) 表示事件发生的概率,取值范围 0≤p(x)≤10 \leq p(x) \leq 10≤p(x)≤1

这个定义式是人为定义设计的,为什么这么定义呢?
- 根据定义,概率p(x)p(x)p(x)和信息量I(x)I(x)I(x)是负相关的,暂且定义为反比例函数,I(x):=1p(x)I(x) := \frac{1}{p(x)}I(x):=p(x)1
- 根据性质两个事件同时发生的信息量等于两个事件的信息量相加,即I(AB)=I(A)+I(B)I(AB) = I(A) + I(B)I(AB)=I(A)+I(B),由此推导出I(x)=log2(1p(x))I(x) = log_2(\frac{1}{p(x)})I(x)=log2(p(x)1)。所以用了对数的加法性质。
- 以2为底,是转换到二进制下的表示复杂度,(其实以e为底、以10为底都可以,只不过以2为底更优)
这里验证一下独立事件的性质:
I(AB)=log2(1p(AB))=log2(1p(A)p(B))=log2(1p(A))+log2(1p(B))=I(A)+I(B)I(AB) = \log_2\left(\frac{1}{p(AB)}\right) = \log_2\left(\frac{1}{p(A)p(B)}\right) = \log_2\left(\frac{1}{p(A)}\right) + \log_2\left(\frac{1}{p(B)}\right) = I(A) + I(B) I(AB)=log2(p(AB)1)=log2(p(A)p(B)1)=log2(p(A)1)+log2(p(B)1)=I(A)+I(B)
举个例子:抛规则和不规则的硬币

2、熵 Entropy
-
定义:概率分布的信息量期望:H(p):=E(I(x))H(p) := E(I(x))H(p):=E(I(x))
亦可理解为:系统整体的信息量。其中,系统整体由所有可能发生的事件构成。比如抛硬币,正面和反面就构成一个系统整体 -
公式:
H(p)=∑piIip=−∑pilog2(pi)H(p) = \sum p_i I_i^p = -\sum p_i log_2(p_i) H(p)=∑piIip=−∑pilog2(pi)
例子:假设一个系统含有两个事件,两个概率构成了概率分布
- 事件A:p(A)=0.2p_{(A)} = 0.2p(A)=0.2,I(A)=log2(1/p(A))=2.32I_{(A)} = log_2(1/p_{(A)}) = 2.32I(A)=log2(1/p(A))=2.32
- 事件B:p(B)=0.8p_{(B)} = 0.8p(B)=0.8,I(B)=log2(1/p(B))=0.32I_{(B)} = log_2(1/p_{(B)}) = 0.32I(B)=log2(1/p(B))=0.32
想用一个值来衡量这个系统所携带的信息量,用熵来表示,是概率分布的期望(所有事件的信息量的加权平均值,概率为权重)
H(p)=0.2⋅2.32+0.8⋅0.32=0.72H(p) = 0.2 \cdot 2.32 + 0.8 \cdot 0.32 = 0.72H(p)=0.2⋅2.32+0.8⋅0.32=0.72
- 作用:用来评估概率模型的不确定性程度
- 不确定性越大,熵越大
- 不确定性越小,熵越小、
这里举个例子,平均分别和正态分布,平均分布的不确定性更高,因为每个事件发生的概率都相等,不确定哪个事情更会发生。

这里举个例子:
例1:抛硬币,正面概率 p(A)=0.5p_{(A)} = 0.5p(A)=0.5,反面概率 p(B)=0.5p_{(B)} = 0.5p(B)=0.5
H(p)=∑piIip=p(A)⋅log2(1p(A))+p(B)⋅log2(1p(B))=0.5⋅log2(10.5)+0.5⋅log2(10.5)=0.5⋅1+0.5⋅1=1\begin{align*} H(p) &= \sum p_i I_i^p \\ &= p_{(A)} \cdot \log_2\left(\frac{1}{p_{(A)}}\right) + p_{(B)} \cdot \log_2\left(\frac{1}{p_{(B)}}\right) \\ &= 0.5 \cdot \log_2\left(\frac{1}{0.5}\right) + 0.5 \cdot \log_2\left(\frac{1}{0.5}\right) \\ &= 0.5 \cdot 1 + 0.5 \cdot 1 \\ &= 1 \end{align*} H(p)=∑piIip=p(A)⋅log2(p(A)1)+p(B)⋅log2(p(B)1)=0.5⋅log2(0.51)+0.5⋅log2(0.51)=0.5⋅1+0.5⋅1=1
例2:抛硬币,正面概率 p(A)=0.2p_{(A)} = 0.2p(A)=0.2,反面概率 p(B)=0.8p_{(B)} = 0.8p(B)=0.8
H(p)=∑piIip=p(A)⋅log2(1p(A))+p(B)⋅log2(1p(B))=0.2⋅log2(10.2)+0.8⋅log2(10.8)=0.2⋅2.32+0.8⋅0.32=0.72\begin{align*} H(p) &= \sum p_i I_i^p \\ &= p_{(A)} \cdot \log_2\left(\frac{1}{p_{(A)}}\right) + p_{(B)} \cdot \log_2\left(\frac{1}{p_{(B)}}\right) \\ &= 0.2 \cdot \log_2\left(\frac{1}{0.2}\right) + 0.8 \cdot \log_2\left(\frac{1}{0.8}\right) \\ &= 0.2 \cdot 2.32 + 0.8 \cdot 0.32 \\ &= 0.72 \end{align*} H(p)=∑piIip=p(A)⋅log2(p(A)1)+p(B)⋅log2(p(B)1)=0.2⋅log2(0.21)+0.8⋅log2(0.81)=0.2⋅2.32+0.8⋅0.32=0.72
- 结论 :
- 若概率密度均匀,产生的随机变量的不确定性就更高,则熵的值就更大
- 若概率密度聚拢,产生的随机变量的不确定性就更低,则熵的值较小
3、交叉熵 Cross Entropy
- 假设:真实概率分布为 ppp、预测概率分布(估计概率分布)为 qqq
- 定义:预测概率分布 qqq 对真实的概率分布 ppp 的平均信息量的估计,叫做交叉熵
- 公式:H(p,q)=∑piIiq=−∑pilog2(qi)H(p,q) = \sum p_i I_i^q = -\sum p_i \log_2(q_i) H(p,q)=∑piIiq=−∑pilog2(qi)
- 和熵的计算公式相比,概率用的是真实分布的概率,信息量用的是预测概率分布的信息量
例1:抛硬币,正面真实概率p(A)=0.5p(A) = 0.5p(A)=0.5,反面真实概率 p(B)=0.5p(B) = 0.5p(B)=0.5;正面估计概率 q(A)=0.2q(A) = 0.2q(A)=0.2,反面估计概率 q(B)=0.8q(B) = 0.8q(B)=0.8
H(p,q)=−∑pilog2(qi)=p(A)⋅log2(1q(A))+p(B)⋅log2(1q(B))=0.5⋅log2(10.2)+0.5⋅log2(10.8)=0.5⋅2.32+0.5⋅0.32=1.32\begin{align*} H(p,q) &= -\sum p_i \log_2(q_i) \\ &= p_{(A)} \cdot \log_2\left(\frac{1}{q_{(A)}}\right) + p_{(B)} \cdot \log_2\left(\frac{1}{q_{(B)}}\right) \\ &= 0.5 \cdot \log_2\left(\frac{1}{0.2}\right) + 0.5 \cdot \log_2\left(\frac{1}{0.8}\right) \\ &= 0.5 \cdot 2.32 + 0.5 \cdot 0.32 \\ &= 1.32 \end{align*} H(p,q)=−∑pilog2(qi)=p(A)⋅log2(q(A)1)+p(B)⋅log2(q(B)1)=0.5⋅log2(0.21)+0.5⋅log2(0.81)=0.5⋅2.32+0.5⋅0.32=1.32
例2:抛硬币,正面真实概率 p(A)=0.5p(A) = 0.5p(A)=0.5,反面真实概率 p(B)=0.5p(B) = 0.5p(B)=0.5;正面估计概率 q(A)=0.4q(A) = 0.4q(A)=0.4,反面估计概率 q(B)=0.6q(B) = 0.6q(B)=0.6
H(p,q)=−∑pilog2(qi)=p(A)⋅log2(1q(A))+p(B)⋅log2(1q(B))=0.5⋅log2(10.4)+0.5⋅log2(10.6)=0.5⋅1.32+0.5⋅0.74=1.03\begin{align*} H(p,q) &= -\sum p_i \log_2(q_i) \\ &= p_{(A)} \cdot \log_2\left(\frac{1}{q_{(A)}}\right) + p_{(B)} \cdot \log_2\left(\frac{1}{q_{(B)}}\right) \\ &= 0.5 \cdot \log_2\left(\frac{1}{0.4}\right) + 0.5 \cdot \log_2\left(\frac{1}{0.6}\right) \\ &= 0.5 \cdot 1.32 + 0.5 \cdot 0.74 \\ &= 1.03 \end{align*} H(p,q)=−∑pilog2(qi)=p(A)⋅log2(q(A)1)+p(B)⋅log2(q(B)1)=0.5⋅log2(0.41)+0.5⋅log2(0.61)=0.5⋅1.32+0.5⋅0.74=1.03
- 结论
- 预估概率分布与真实概率分布越接近,交叉熵越小。
- 交叉熵的值总是大于真实概率分布的熵的值。证明是根据吉布斯不等式。
吉布斯不等式:
若 ∑i=1npi=∑i=1nqi=1\sum_{i=1}^{n} p_i = \sum_{i=1}^{n} q_i = 1∑i=1npi=∑i=1nqi=1,且 pi,qi∈(0,1]p_i, q_i \in (0,1]pi,qi∈(0,1],则有:
−∑i=1npilogpi≤−∑i=1npilogqi-\sum_{i=1}^{n} p_i \log p_i \leq -\sum_{i=1}^{n} p_i \log q_i −i=1∑npilogpi≤−i=1∑npilogqi
等号成立当且仅当 pi=qi∀ip_i = q_i \forall ipi=qi∀i
4、相对熵 Relative Entropy 、KL散度 KL Divergence
-
名称:KL散度以Kullback和Leibler的名字命名,也被称为相对熵
-
作用:用于衡量2个概率分布之间的差异,理解为两个分布信息量的差异
-
公式:
DKL(p∣∣q)=∑pi[Iq−Ip]#Iq−Ip为信息量之差=∑pi[log2(1qi)−log2(1pi)]=∑pilog2(1qi)−∑pilog2(1pi)=H(p,q)−H(p)#交叉熵减去前者基准分布P的熵=∑pilog2(piqi)\begin{align*} D_{KL}(p \vert \vert q) &= \sum p_i [I_q - I_p] \quad \# I_q - I_p \text{为信息量之差} \\ &= \sum p_i \left[ \log_2\left(\frac{1}{q_i}\right) - \log_2\left(\frac{1}{p_i}\right) \right] \\ &= \sum p_i \log_2\left(\frac{1}{q_i}\right) - \sum p_i \log_2\left(\frac{1}{p_i}\right) \\ &= H(p,q) - H(p) \quad \# 交叉熵减去前者基准分布P的熵 \\ &= \sum p_i \log_2\left(\frac{p_i}{q_i}\right) \end{align*} DKL(p∣∣q)=∑pi[Iq−Ip]#Iq−Ip为信息量之差=∑pi[log2(qi1)−log2(pi1)]=∑pilog2(qi1)−∑pilog2(pi1)=H(p,q)−H(p)#交叉熵减去前者基准分布P的熵=∑pilog2(qipi)
其中交叉熵 H(p,q)=∑piIiq=∑pilog2(1qi)H(p,q) = \sum p_i I_i^q = \sum p_i \log_2\left(\frac{1}{q_i}\right)H(p,q)=∑piIiq=∑pilog2(qi1)
- 重要性质:
-
恒为正:D(p∣∣q)≥0D(p \vert \vert q) \geq 0D(p∣∣q)≥0
由吉布斯不等式可知:D(p∣∣q)≥0D(p \vert \vert q) \geq 0D(p∣∣q)≥0;当分布qqq和分布ppp完全一样时,D(p∣∣q)=0D(p \vert \vert q) = 0D(p∣∣q)=0吉布斯不等式说明:若∑i=1npi=∑i=1nqi=1\sum_{i=1}^{n} p_i = \sum_{i=1}^{n} q_i = 1∑i=1npi=∑i=1nqi=1,且pi,qi∈(0,1]p_i, q_i \in (0,1]pi,qi∈(0,1],则有:
−∑i=1npilogpi≤−∑i=1npilogqi-\sum_{i=1}^{n} p_i \log p_i \leq -\sum_{i=1}^{n} p_i \log q_i −i=1∑npilogpi≤−i=1∑npilogqi
等号成立当且仅当pi=qi∀ip_i = q_i \forall ipi=qi∀i -
没有‘交换律: D(p∣∣q)D(p \vert \vert q)D(p∣∣q)与D(q∣∣p)D(q \vert \vert p)D(q∣∣p)不一样,
即D(p∣∣q)≠D(q∣∣p)D(p \vert \vert q) \neq D(q \vert \vert p)D(p∣∣q)=D(q∣∣p),可以认为把前面的分别当做真实分布,计算后面的预测分布与之的差异- D(p∣∣q)D(p \vert \vert q)D(p∣∣q)表示以ppp为基准(为真实概率分布),估计概率分布qqq与真实概率分布ppp之间的差距
- D(q∣∣p)D(q \vert \vert p)D(q∣∣p)表示以qqq为基准(为真实概率分布),估计概率分布ppp与真实概率分布qqq之间的差距
4、交叉熵损失 Cross Entropy Loss
由上可知,KL散度D(p∣∣q)D(p \vert \vert q)D(p∣∣q)表示预测分布qqq与真实分布ppp之间的差距,所以我们可直接将损失函数定义为KL散度。
并且我们希望损失值越小越好,模型的预测分布qqq与真实分布ppp完全相同,即:损失函数Loss=D(p∣∣q)=0Loss = D(p \vert \vert q) = 0Loss=D(p∣∣q)=0。
损失函数:Loss=D(p∣∣q)=H(p,q)−H(p)=∑pilog2(1qi)−∑pilog2(1pi)(1)Loss = D(p \vert \vert q) = H(p, q) - H(p) = \sum p_i \log_2\left(\frac{1}{q_i}\right) - \sum p_i \log_2\left(\frac{1}{p_i}\right) \tag1Loss=D(p∣∣q)=H(p,q)−H(p)=∑pilog2(qi1)−∑pilog2(pi1)(1)
下面对公式(1)进行化简
交叉熵损失一般用与分类任务。对于分类问题,真实分布的One-Hot编码是一个单点分布,真实类别的概率为1,其他类别的概率都为0,类似如下:
| 类别 | class1 | class 2 | class 3 | class 4 |
|---|---|---|---|---|
| 概率 | 0 | 0 | 1 | 0 |
- pclass1=pclass2=pclass4=0p_{class1} = p_{class2} = p_{class4} = 0pclass1=pclass2=pclass4=0,其他类别的概率为零,权重为0就不用算信息量了
- log2(1pclass3)=0\log_2\left(\frac{1}{p_{class3}}\right) = 0log2(pclass31)=0,类别3的信息量为0
- 所以,H(p)=∑pilog2(1pi)=0H(p) = \sum p_i \log_2\left(\frac{1}{p_i}\right) = 0H(p)=∑pilog2(pi1)=0。
损失函数(1)可进一步化简为:
Loss=D(p∣∣q)=H(p,q)−H(p)=H(p,q)(2)Loss = D(p \vert \vert q) = H(p, q) - H(p) = H(p, q) \tag2 Loss=D(p∣∣q)=H(p,q)−H(p)=H(p,q)(2)
H(p,q)H(p, q)H(p,q)是交叉熵,所以损失函数又称为交叉熵损失函数:
Cross_Entropy_Loss=H(p,q)=−∑pilog2(qi)(3)Cross\_Entropy\_Loss = H(p, q) = -\sum p_i \log_2(q_i) \tag3Cross_Entropy_Loss=H(p,q)=−∑pilog2(qi)(3)
又因为真实分布为单点分布,真实类别的概率pclass=1p_{class} = 1pclass=1,其他类别的概率pclass‾=0p_{\overline{class}} = 0pclass=0,所以
Cross_Entropy_Loss=H(p,q)=−log2(qclass)Cross\_Entropy\_Loss = H(p, q) = -\log_2(q_{class})Cross_Entropy_Loss=H(p,q)=−log2(qclass)
二、交叉熵损失函数
交叉熵损失函数拆解
交叉熵损失多用于多分类任务,下面我们通过拆解交叉熵的公式来理解其作为损失函数的意义。
假设我们在做一个n分类的问题,模型预测的输出结果是[x1,x2,x3,…,xn][x_1, x_2, x_3, \dots, x_n][x1,x2,x3,…,xn],然后,我们选择交叉熵损失函数作为目标函数,通过反向传播调整模型的权重。
交叉熵损失函数的公式:
loss(x,class)=−log(ex[class]∑jexj)=−x[class]+log(∑jexj)\begin{align*} loss(x, class) &= -\log\left(\frac{e^{x_{[class]}}}{\sum_j e^{x_j}}\right) \\ &= -x_{[class]} + \log\left(\sum_j e^{x_j}\right) \end{align*} loss(x,class)=−log(∑jexjex[class])=−x[class]+log(j∑exj)
- xxx是预测结果,是一个向量x=[x1,x2,x3,…,xn]x = [x_1, x_2, x_3, \dots, x_n]x=[x1,x2,x3,…,xn],其元素个数和类别数一样多。
- classclassclass表示这个样本的实际标签,比如,样本实际属于分类2,那么class=2class = 2class=2,x[class]x_{[class]}x[class]就是x2x_2x2,就是取预测结果向量中的第二个元素,即,取其真实分类对应的那个类别的预测值。
接下来,我们来拆解公式,理解公式:
-
首先,交叉熵损失函数中包含了一个最基础的部分:
softmax(xi)=exi∑j=0nexjsoftmax(x_i) = \frac{e^{x_i}}{\sum_{j = 0}^{n} e^{x_j}}softmax(xi)=∑j=0nexjexi
softmax 将分类的结果做了归一化:- exe^xex的作用是将xxx转换为非负数
- 通过 softmax 公式exi∑j=0nexj\frac{e^{x_i}}{\sum_{j = 0}^{n} e^{x_j}}∑j=0nexjexi计算出该样本被分到类别iii的概率,这里所有分类概率相加的总和等于1
-
我们想要使预测结果中,真实分类的那个概率接近100%。我们取出真实类别的那个概率,(下标为class):ex[class]∑j=0nexj\frac{e^{x_{[class]}}}{\sum_{j = 0}^{n} e^{x_j}}∑j=0nexjex[class],我们希望它的值是100%
-
作为损失函数,后面需要参与求导。乘/除法表达式求导比较麻烦,所以最好想办法转化成加/减法表达式。最自然的想法是取对数,把乘除法转化为加减法表达式:
logex[class]∑j=0nexj=logex[class]−log∑j=0nexj\log\frac{e^{x_{[class]}}}{\sum_{j = 0}^{n} e^{x_j}} = \log e^{x_{[class]}} - \log \sum_{j = 0}^{n} e^{x_j} log∑j=0nexjex[class]=logex[class]−logj=0∑nexj- 由于对数单调增,那么,求ex[class]∑j=0nexj\frac{e^{x_{[class]}}}{\sum_{j = 0}^{n} e^{x_j}}∑j=0nexjex[class]的最大值的问题,可以转化为求logex[class]∑j=0nexj\log\frac{e^{x_{[class]}}}{\sum_{j = 0}^{n} e^{x_j}}log∑j=0nexjex[class]的最大值的问题。
- ex[class]∑j=0nexj\frac{e^{x_{[class]}}}{\sum_{j = 0}^{n} e^{x_j}}∑j=0nexjex[class]的取值范围是(0,1)(0, 1)(0,1),最大值为1。取对数之后,logex[class]∑j=0nexj\log\frac{e^{x_{[class]}}}{\sum_{j = 0}^{n} e^{x_j}}log∑j=0nexjex[class]的取值范围为[−∞,0][-\infty, 0][−∞,0],最大值为0
-
作为损失函数的意义是:当预测结果越接近真实值,损失函数的值越接近于0
所以,我们把logex[class]∑j=0nexj\log\frac{e^{x_{[class]}}}{\sum_{j = 0}^{n} e^{x_j}}log∑j=0nexjex[class]取反之后,−logex[class]∑j=0nexj-\log\frac{e^{x_{[class]}}}{\sum_{j = 0}^{n} e^{x_j}}−log∑j=0nexjex[class]最小值为0
这样就能保证当ex[class]∑j=0nexj\frac{e^{x_{[class]}}}{\sum_{j = 0}^{n} e^{x_j}}∑j=0nexjex[class]越接近于100%,loss=−log(ex[class]∑j=0nexj)loss = -\log\left(\frac{e^{x_{[class]}}}{\sum_{j = 0}^{n} e^{x_j}}\right)loss=−log(∑j=0nexjex[class])越接近0。
代码实现nn.CrossEntropyLoss
nn.CrossEntropyLoss(weight=None, reduction='mean',ignore_index=-100)
weight(optional): 一个张量,用于为每个类别的 loss 设置权值。可以用于处理类别不平衡的情况。- 默认值为
None weight必须是float类型的tensor,其长度要与类别个数一致,即每一个类别都要设置权重值
loss(x,class)=weight[class](−log(ex[class]∑jexj))loss(x, class) = weight_{[class]} \left(-\log\left(\frac{e^{x_{[class]}}}{\sum_j e^{x_j}}\right)\right) loss(x,class)=weight[class](−log(∑jexjex[class]))
- 默认值为
reduction(string, optional): 指定损失的计算方式,可选值有:"none"、"mean"、"sum""none":表示不进行任何降维,返回每个样本的损失"mean": 表示对参与计算的样本的损失取平均值,("mean"为默认值)"sum": 表示对参与计算的样本的损失求和
ignore_index(int, optional): 忽略目标中的特定类别索引,不计入损失计算。默认值为-100
代码示例:
假设有4张图片(batch_size=4),需要把这4张图片分类到5个类别(鸟,狗,猫,汽车,船)上去。经过网络得到的预测结果为predict,尺寸是[4, 5];其真实标签为label,尺寸是[4]。接下来使用nn.CrossEntropyLoss()计算预测结果predict和真实值label的交叉熵损失。
import torch
import torch.nn as nn# -----------------------------------------
# 定义数据: batch_size=4; 一共有5个分类
# label.size() : torch.Size([4])
# predict.size(): torch.Size([4, 5])
# -----------------------------------------
torch.manual_seed(100)
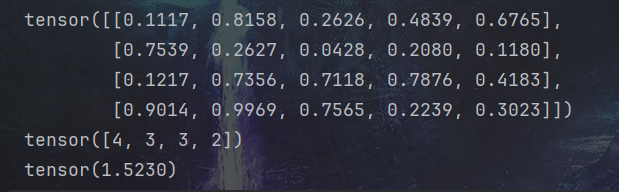
predict = torch.rand(4, 5)
label = torch.tensor([4, 3, 3, 2])
print(predict)
print(label)# -----------------------------------------
# 直接调用函数 nn.CrossEntropyLoss() 计算 Loss
# -----------------------------------------
criterion = nn.CrossEntropyLoss()
loss = criterion(predict, label)
print(loss)
三、二元交叉熵损失函数 Binary Cross Entropy Loss
1、二元交叉熵损失函数
(1)二元交叉熵损失函数(Binary Cross Entropy Loss)适用于二分类问题:样本标签为二元值:0 或 1。
(2)用于将模型预测值和真实值之间的差异转化为一个标量值,从而衡量模型预测的准确性。
计算公式:
L=−1N∑i=1N[yilog(y^i)+(1−yi)log(1−y^i)]L = -\frac{1}{N} \sum_{i=1}^{N} \left[ y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i) \right] L=−N1i=1∑N[yilog(y^i)+(1−yi)log(1−y^i)]
其中:
- NNN 表示样本数量
- yiy_iyi 表示第 iii 个样本的真实标签:0 or 1
- y^i\hat{y}_iy^i 表示第 iii 个样本的预测值
如果 yi=1y_i = 1yi=1,则第一项 yilog(y^i)y_i \log(\hat{y}_i)yilog(y^i) 生效,第二项 (1−yi)log(1−y^i)(1 - y_i) \log(1 - \hat{y}_i)(1−yi)log(1−y^i) 失效;如果 yi=0y_i = 0yi=0,则第一项 yilog(y^i)y_i \log(\hat{y}_i)yilog(y^i) 失效,第二项 (1−yi)log(1−y^i)(1 - y_i) \log(1 - \hat{y}_i)(1−yi)log(1−y^i) 生效。
2、nn.BCELoss() 类
nn.BCELoss() 是 PyTorch 实现的二元交叉熵损失函数,也称为对数损失函数(Log Loss)。
torch.nn.BCELoss(weight=None, size_average=None, reduce=None, reduction='mean')
参数说明:
weight:用于样本加权的权重张量。如果给定,则必须是一维张量,大小等于输入张量的大小。默认值为None。reduction:指定如何计算损失值。可选值为'none'、'mean'或'sum'。默认值为'mean'。
3、使用场景举例
假设有一个二分类任务:判断图片中是否包含猫。该图像的标签值为 0 或 1。我们可以定义一个二元分类模型,用 Sigmoid 输出一个概率值,表示样本属于猫的概率。
import torch
import torch.nn as nnclass CatClassifier(nn.Module):def __init__(self):super(CatClassifier, self).__init__()self.fc = nn.Linear(5, 1)self.sigmoid = nn.Sigmoid()def forward(self, x):x = x.view(x.size(0), -1)x = self.fc(x)x = self.sigmoid(x)return xmodel = CatClassifier()
criterion = nn.BCELoss()x = torch.rand((3, 5))
label = torch.tensor([0, 1, 1], dtype=torch.float32)
pred = model(x) # tensor([[0.6140],[0.5350],[0.5852]], grad_fn=<SigmoidBackward0>)
loss = criterion(pred.squeeze(), label)
print(loss)
4、torch.nn.BCEWithLogitsLoss() 与 nn.BCELoss() 的区别
nn.BCELoss()的输入是二元分类模型的预测值 y^\hat{y}y^ 和实际标签 yyy。并且 y^\hat{y}y^ 的范围是$[0,1]),因为二元分类模型内部已经对预测结果做了sigmoid处理。
公式:
nn.BCELoss()=−1N∑i=1N[yilog(y^i)+(1−yi)log(1−y^i)]nn.BCELoss() = -\frac{1}{N} \sum_{i=1}^{N} \left[ y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i) \right] nn.BCELoss()=−N1i=1∑N[yilog(y^i)+(1−yi)log(1−y^i)]torch.nn.BCEWithLogitsLoss()的输入也是二元分类模型的输出值 zzz 和实际标签 yyy,不同的是输出 zzz 在模型内部没有经过sigmoid处理,是任意实数。这种情况下,sigmoid处理就被放到了损失函数中。
所以,torch.nn.BCEWithLogitsLoss()函数内部的计算过程是先对 zzz 应用sigmoid函数,将其映射到[0,1][0,1][0,1]范围内,然后再使用二元交叉熵计算预测值和实际标签之间的损失值。
公式:
nn.BCEWithLogitsLoss()=−1N∑i=1N[yilogσ(zi)+(1−yi)log(1−σ(zi))]nn.BCEWithLogitsLoss() = -\frac{1}{N} \sum_{i=1}^{N} \left[ y_i \log \sigma(z_i) + (1 - y_i) \log(1 - \sigma(z_i)) \right] nn.BCEWithLogitsLoss()=−N1i=1∑N[yilogσ(zi)+(1−yi)log(1−σ(zi))]- 另外,
torch.nn.BCEWithLogitsLoss()还支持设置pos_weight参数,用于处理样本不平衡的问题。而nn.BCELoss()不支持设置pos_weight参数。
5、torch.nn.BCEWithLogitsLoss() 类
torch.nn.BCEWithLogitsLoss(weight=None,size_average=None,reduce=None,reduction='mean',pos_weight=None)
参数:
weight:用于对每个样本的损失值进行加权。默认值为None。reduction:指定如何对每个batch的损失值进行降维。可选值为'none'、'mean'和'sum'。默认值为'mean'。pos_weight:用于对正样本的损失值进行加权。可以用于处理样本不平衡的问题。例如,如果正样本比负样本少很多,可以设置pos_weight为一个较大的值,以提高正样本的权重。默认值为None。
