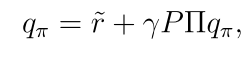强化学习-CH2 状态价值和贝尔曼等式
强化学习-CH2 状态值和贝尔曼等式
状态值(State Value)它被定义为agent在遵循给定策略时所能获得的平均奖励。 状态值越大,对应的策略越好。 状态值可以用作评估策略是否良好的度量。Bellman方程描述了所有状态值之间的关系。 通过求解Bellman方程,可以得到状态值。 这个过程被称为策略评估,这是强化学习中的一个基本概念。
2.1 计算回报(returns)的两种方式
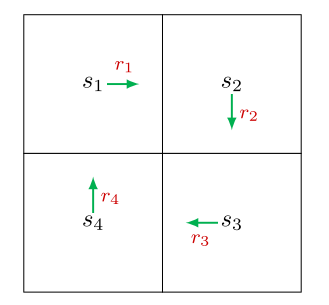
针对上图的网格世界,计算回报有两种方式:
(1)按照定义:回报等于沿一条轨迹收集的所有奖励的折现总和。
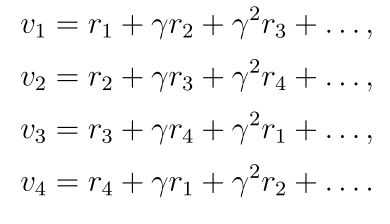
vi表示从si出发所得到的回报(奖励总和)。
(2)自举:
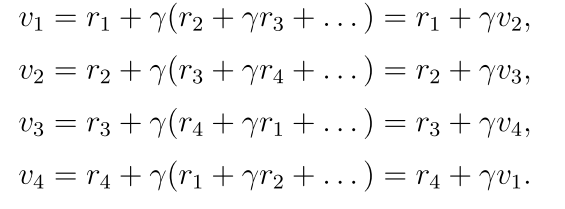
上述等式可以写成矩阵形式:
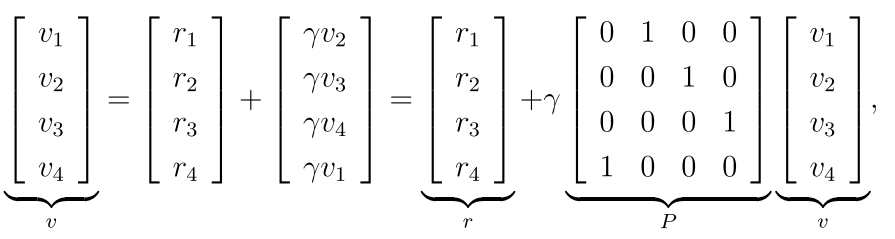
有:
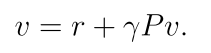
状态值就可以计算:
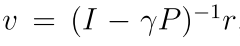
2.2 状态值(State Values)
从t时刻起,得到一条轨迹
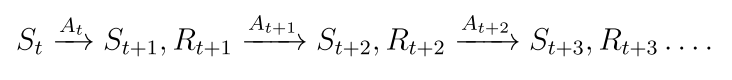
St,At,Rt表示状态,动作,奖励,他们都是随机变量
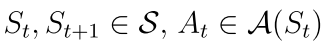
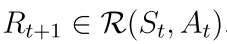
这条轨迹的回报是:
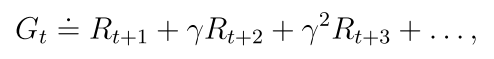
Gt也是随机变量,可以计算它的期望
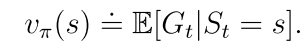
vπ(s)表示状态s的值,它只依赖于s(从s出发)和策略π
状态值与回报之间的关系进一步阐明如下。 当策略和系统模型都是确定的时,从一个状态开始总是会导致相同的轨迹。 在这种情况下,从一个状态开始获得的回报等于该状态的值。 相比之下,当策略或系统模型是随机的,从相同的状态出发可能会产生不同的轨迹。 在这种情况下,不同轨迹的收益是不同的,状态值是这些收益的均值。
状态值:在给定策略π下,从一个状态出发,获取到的回报的均值。
2.3 贝尔曼(Bellman)公式
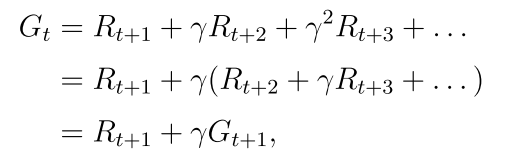
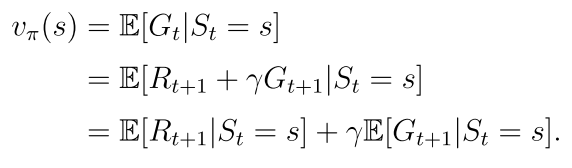
等式右边的第一项表示立即回报
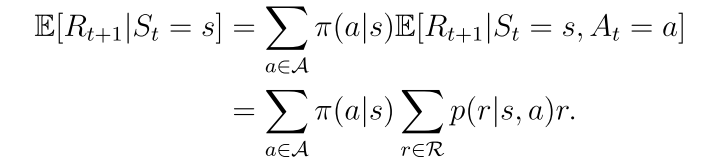
第二项表示未来回报的期望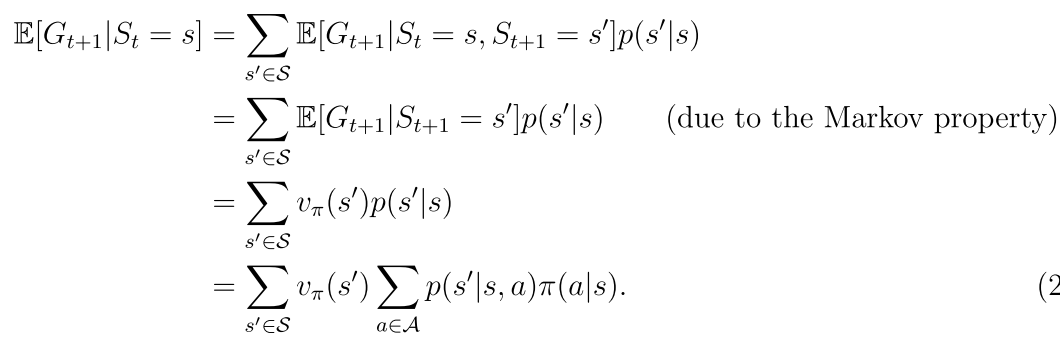
因此原等式可以写成以下形式:
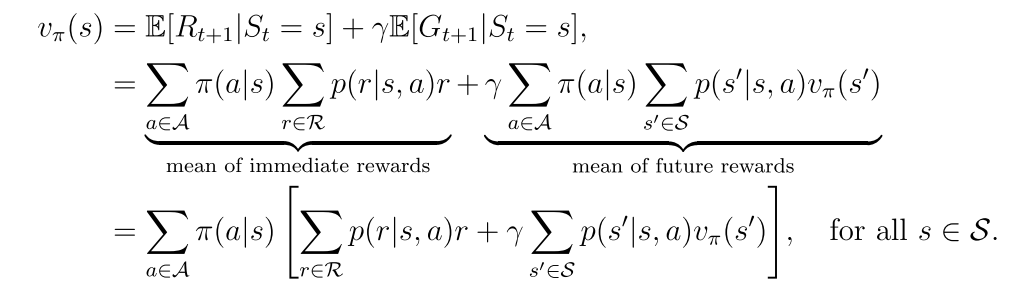
上式就是贝尔曼公式,它体现了所有状态值之间的关系,从贝尔曼公式计算状态的过程就称为策略评估过程。
p(r|s,a)和p(s’|s,a)代表系统模型
2.4 贝尔曼公式的向量形式
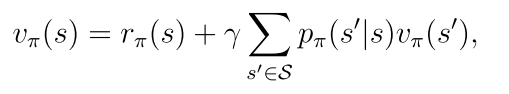
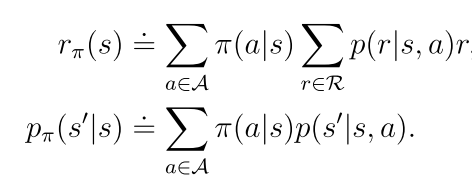
rπ(s)表示立即回报 pπ(s’|s)表示在策略π下从s转移到s’的概率
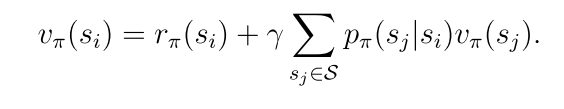
向量形式:
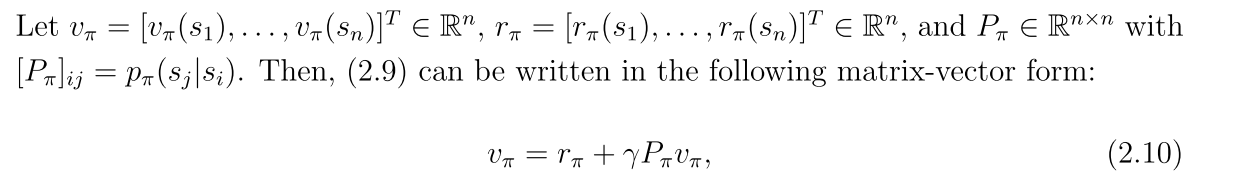
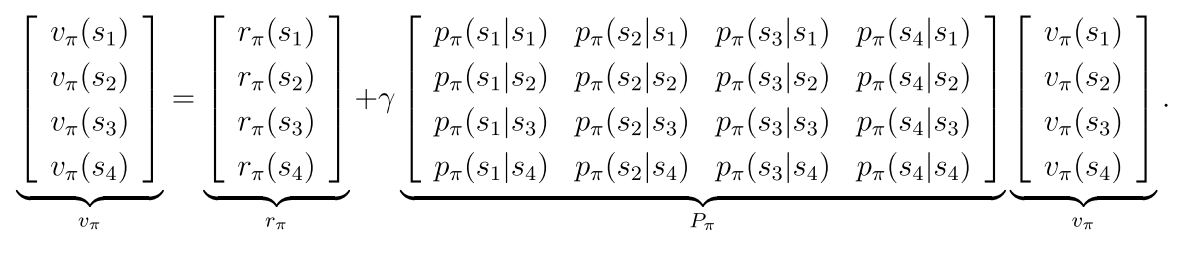
2.5 从贝尔曼公式中求解状态值
2.5.1 Closed-form solution
直接求解
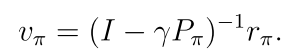
2.5.2 迭代求解
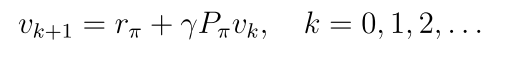
迭代法生成一系列value,其中v0是初始猜测
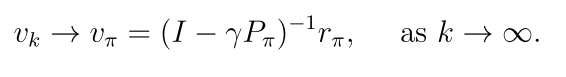
2.6 从状态值到动作值
动作值(action value)在某个状态下采取一个动作的值
一个状态-动作对(s,a)的动作值定义为
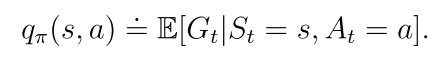
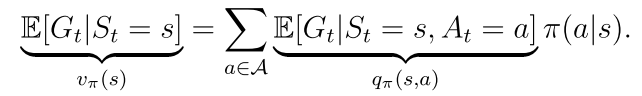
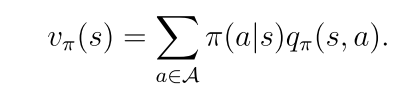
状态值是对与该状态相关联的动作值的期望。
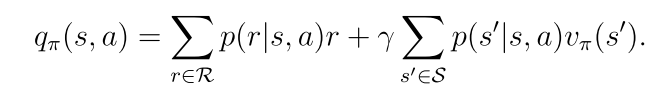
2.7 动作值的贝尔曼公式
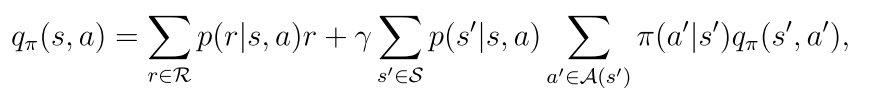
态值是对与该状态相关联的动作值的期望。
[外链图片转存中…(img-Uor3nfEM-1755503156857)]
2.7 动作值的贝尔曼公式
[外链图片转存中…(img-fVdXeNUK-1755503156857)]